- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Элементы релятивистской механики презентация
Содержание
- 1. Элементы релятивистской механики
- 2. ПОСТУЛАТЫ СТО СТО основывается на следующих положениях:
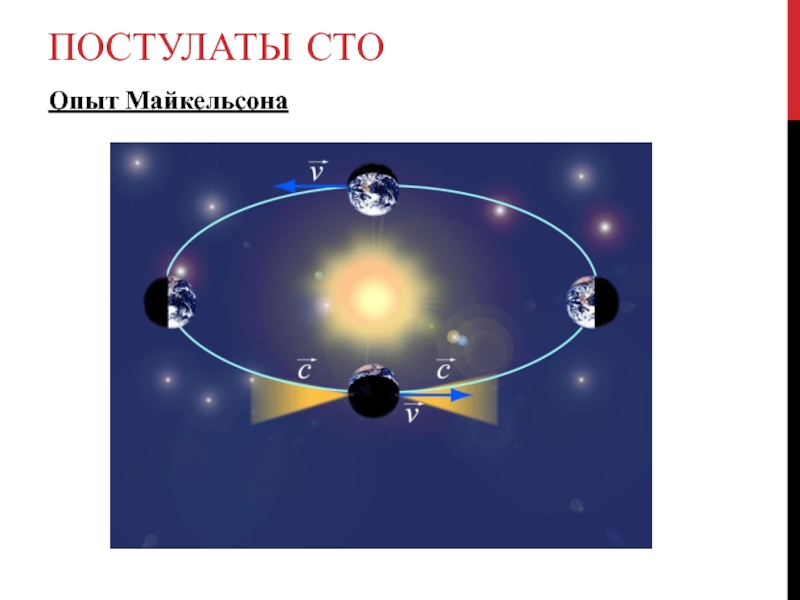
- 3. ПОСТУЛАТЫ СТО Опыт Майкельсона
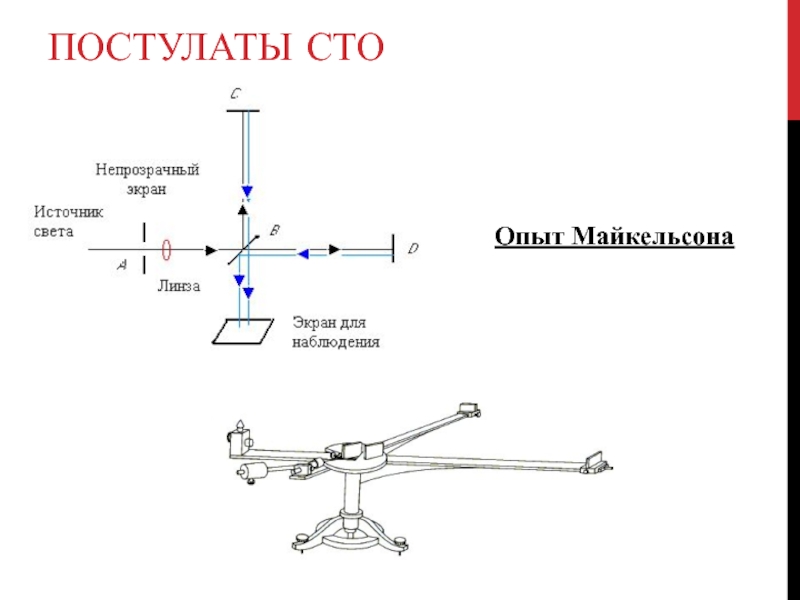
- 4. ПОСТУЛАТЫ СТО Опыт Майкельсона
- 5. ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА Рассмотрим инерциальные системы отсчета K
- 6. ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА Найдем коэффициенты А и B.
- 7. ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА Для нахождения коэффициента A
- 8. ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА Решив данную систему относительно А
- 9. ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА Далее найдем преобразование времени для
- 10. РЕЛЯТИВИСТСКИЙ ЗАКОН СЛОЖЕНИЯ СКОРОСТЕЙ Согласно
- 11. РЕЛЯТИВИСТСКИЙ ЗАКОН СЛОЖЕНИЯ СКОРОСТЕЙ Найдем отношение Δx/Δt,
- 12. СЛЕДСТВИЯ ПРЕОБРАЗОВАНИЙ ЛОРЕНЦА Относительность одновременности событий
- 13. СЛЕДСТВИЯ ПРЕОБРАЗОВАНИЙ ЛОРЕНЦА Сокращение длины
- 14. СЛЕДСТВИЯ ПРЕОБРАЗОВАНИЙ ЛОРЕНЦА Сокращение длины Учитывая, что
- 15. СЛЕДСТВИЯ ПРЕОБРАЗОВАНИЙ ЛОРЕНЦА Длительность события Пусть в
- 16. ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКОЙ ДИНАМИКИ Экспериментальное изучение удельного заряда
- 17. ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКОЙ ДИНАМИКИ Учитывая зависимость массы тела
- 18. ЭНЕРГИЯ В РЕЛЯТИВИСТСКОЙ МЕХАНИКЕ Используем основное уравнение
- 19. ЭНЕРГИЯ В РЕЛЯТИВИСТСКОЙ МЕХАНИКЕ Зная полную энергию
Слайд 2ПОСТУЛАТЫ СТО
СТО основывается на следующих положениях:
принцип относительности Эйнштейна: все законы природы
2. принцип независимости скорости света в инерциальных системах отсчета от скорости движения источника и приемника (скорость света не может превышать ~3∙108 м/с).
Слайд 5ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА
Рассмотрим инерциальные системы отсчета K и K‘. Направим оси координат
Так как системы координат К и К' равноправны, то преобразования координат и времени должны быть такими, чтобы их можно было обращать при переходе от преобразования К→К' к преобразованию К'→ К.
В связи с этим данные преобразования должны быть линейными функциями. Значит функцию x‘ = f(x,t) можно представить в виде
Слайд 6ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА
Найдем коэффициенты А и B. Пусть в начальный момент времени
Т.о., преобразования координат при переходах К'→ К и К→ К' будут иметь вид:
Слайд 7ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА
Для нахождения коэффициента A снова рассмотрим начальный момент времени,
Подставим последние значения x и x' в преобразования x'→x и x→x'. Получим
Слайд 8ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА
Решив данную систему относительно А придём к
Окончательно выражения для преобразований
Слайд 9ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА
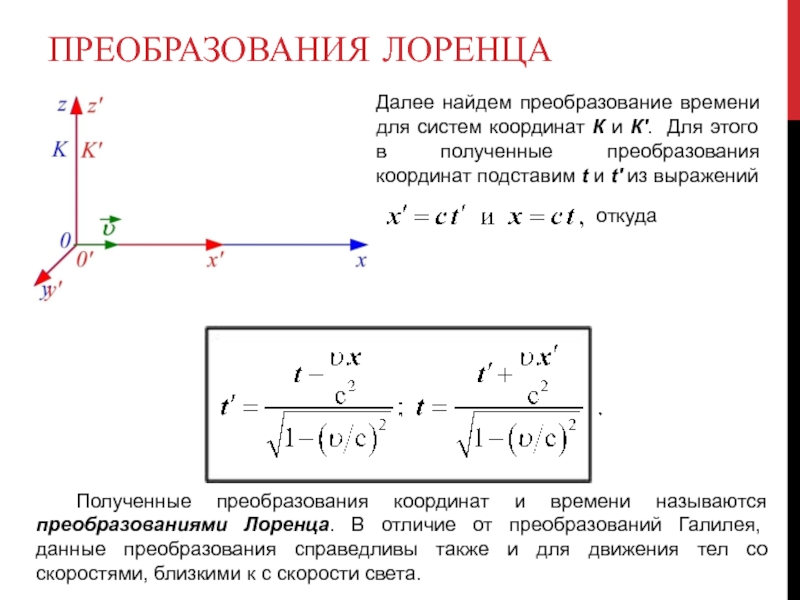
Далее найдем преобразование времени для систем координат К и К'.
откуда
Полученные преобразования координат и времени называются преобразованиями Лоренца. В отличие от преобразований Галилея, данные преобразования справедливы также и для движения тел со скоростями, близкими к с скорости света.
Слайд 10РЕЛЯТИВИСТСКИЙ ЗАКОН СЛОЖЕНИЯ СКОРОСТЕЙ
Согласно преобразованиям Галилея скорость тела U
Данное преобразование противоречит положению СТО о независимости скорости света от скорости источника и приемника света. Получим релятивистский закон сложения скоростей.
Пусть в течении промежутка времени от t1 до t2 координаты тела изменились от x1 до x2 в системе отсчета К . Тогда можно записать. что
Слайд 11РЕЛЯТИВИСТСКИЙ ЗАКОН СЛОЖЕНИЯ СКОРОСТЕЙ
Найдем отношение Δx/Δt, которое имеет смысл скорости перемещения
Полученное соотношение и есть формула релятивистского закона сложения скоростей. Видно, что даже если обе скорости U' и υ равны скорости света c, то U = c.
Слайд 12СЛЕДСТВИЯ ПРЕОБРАЗОВАНИЙ ЛОРЕНЦА
Относительность одновременности событий
Пусть в системе К происходят
Т.о., оказывается, что одновременные события в одной инерциальной системе отсчета не всегда одновременны в другой инерциальной системе отсчета.
Слайд 13СЛЕДСТВИЯ ПРЕОБРАЗОВАНИЙ ЛОРЕНЦА
Сокращение длины
Пусть в системе К' находится стержень.
Слайд 14СЛЕДСТВИЯ ПРЕОБРАЗОВАНИЙ ЛОРЕНЦА
Сокращение длины
Учитывая, что длина стержня в системе отсчета, относительно
Т.о., размеры тела в направлении движения сокращаются. В то же время поперечные размеры (перпендикулярно направлению движения) остаются неизменными.
Слайд 15СЛЕДСТВИЯ ПРЕОБРАЗОВАНИЙ ЛОРЕНЦА
Длительность события
Пусть в системе К' в точке x' происходит
Интервал времени Δt' называется собственным временем события (измерено в той системе отсчета, в которой событие происходит). Как правило данное время обозначают τ0. С учетом этого длительность события τ в системе К рассчитывается по формуле:
Т.о., длительность события минимальна в той системе отсчета, в которой событие происходит. И сокращение размеров тела и увеличение длительности события есть кинематические эффекты, являются проявлениями фундаментальных свойств пространства и времени.
Слайд 16ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКОЙ ДИНАМИКИ
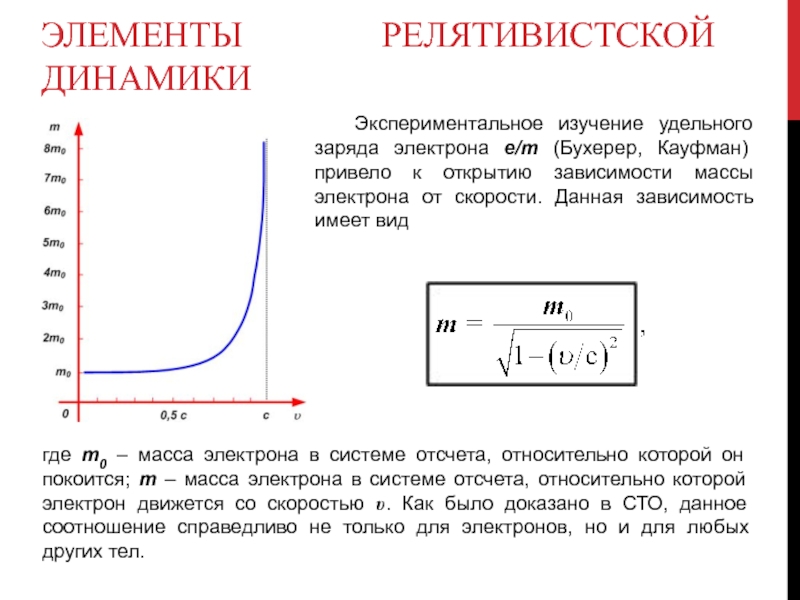
Экспериментальное изучение удельного заряда электрона e/m (Бухерер, Кауфман) привело
где m0 – масса электрона в системе отсчета, относительно которой он покоится; m – масса электрона в системе отсчета, относительно которой электрон движется со скоростью υ. Как было доказано в СТО, данное соотношение справедливо не только для электронов, но и для любых других тел.
Слайд 17ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКОЙ ДИНАМИКИ
Учитывая зависимость массы тела от скорости, релятивистский импульс тела
Отсюда можно получить основное уравнение релятивистской динамики
Слайд 18ЭНЕРГИЯ В РЕЛЯТИВИСТСКОЙ МЕХАНИКЕ
Используем основное уравнение релятивистской динамики для получения релятивистского
Выражение равно - элементарной работе, совершаемой на телом за время dt. Как известно, работа совершаемая над телом равна приращению энергии тела:
Значит
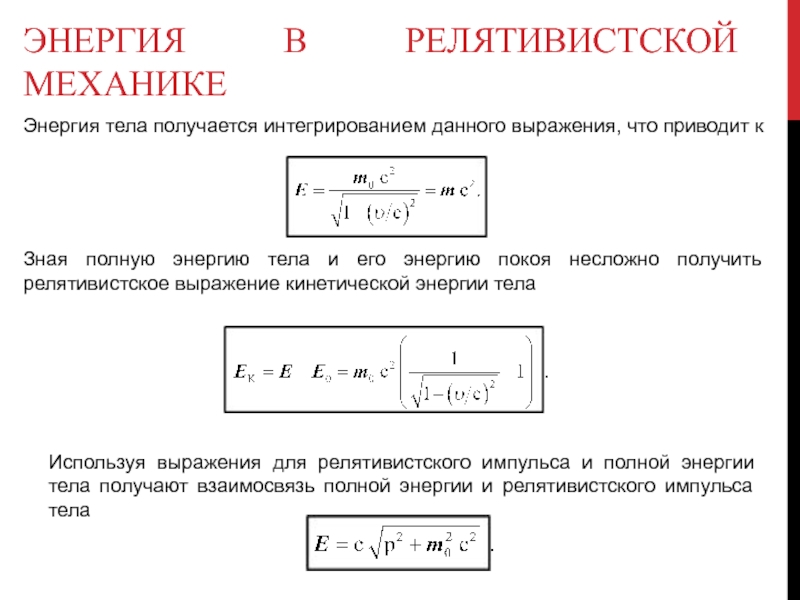
Слайд 19ЭНЕРГИЯ В РЕЛЯТИВИСТСКОЙ МЕХАНИКЕ
Зная полную энергию тела и его энергию покоя
Используя выражения для релятивистского импульса и полной энергии тела получают взаимосвязь полной энергии и релятивистского импульса тела
Энергия тела получается интегрированием данного выражения, что приводит к