- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Техническая термодинамика. Основные понятия и исходные положения термодинамики. (Лекция 1) презентация
Содержание
- 1. Техническая термодинамика. Основные понятия и исходные положения термодинамики. (Лекция 1)
- 2. 1. Основные понятия и законы термодинамики 2.
- 3. 1. Бендерский Б.Я. Техническая термодинамика и теплопередача.
- 4. Термодинамика – наука о закономерностях взаимного преобразования
- 5. Термодинамическая система Термодинамическая система – материальное тело
- 6. Термодинамическая система Различают гомогенные и гетерогенные системы.
- 7. Экстенсивные параметры – характеризуют систему как целое.
- 8. Температура Температура – мера нагретости тела. С
- 9. Давление Давление представляет собой средний результат силового
- 10. Удельный объем Удельный объем – объем единицы
- 11. Уравнение состояния Функциональная зависимость между параметрами простой
- 12. Уравнение состояния Связь между коэффициентом объемного расширения
- 13. Уравнение Ван дер Ваальса Для одного моля
- 14. Уравнение Ван дер Ваальса Поправка к давлению
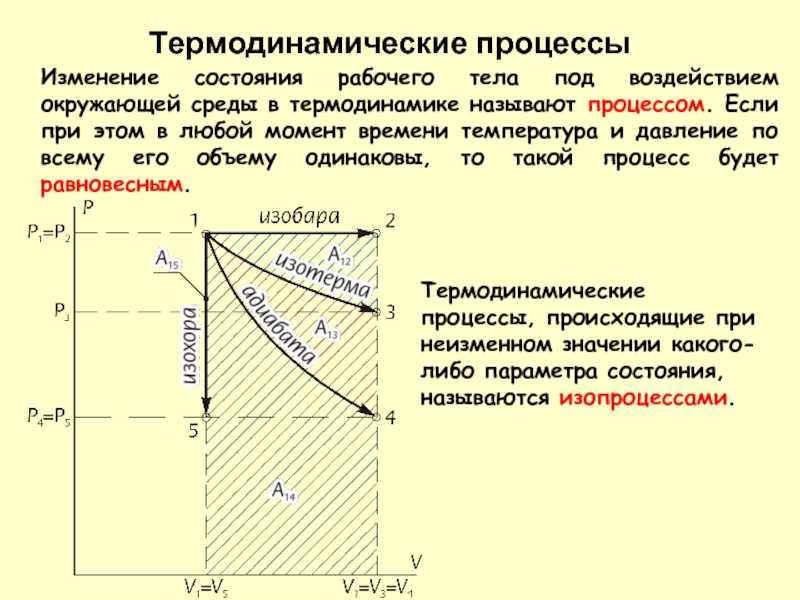
- 16. Термодинамические процессы Изменение состояния рабочего тела под
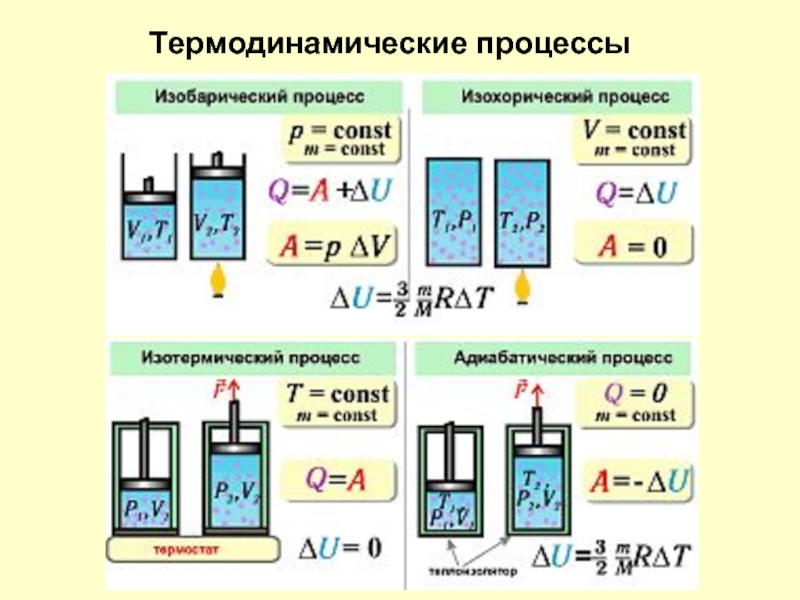
- 17. Термодинамические процессы
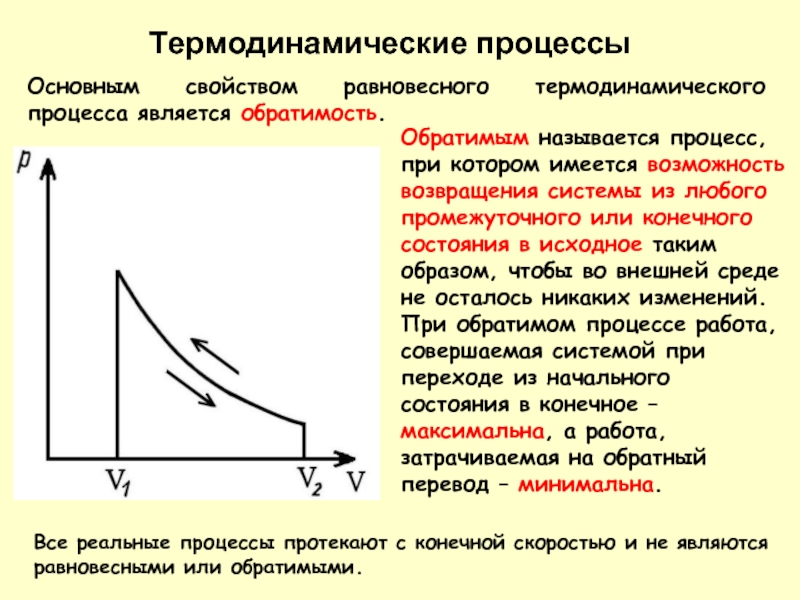
- 18. Термодинамические процессы Основным свойством равновесного термодинамического процесса
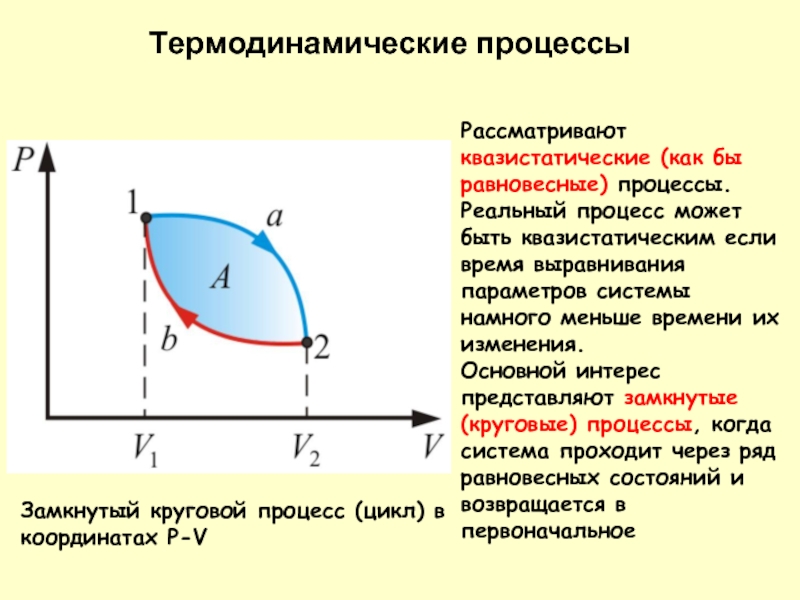
- 19. Термодинамические процессы
- 20. Идеальные газы и их смеси Уравнение состояния
- 21. Идеальные газы и их смеси Для любого
- 22. Идеальные газы и их смеси Газовая смесь
- 23. Идеальные газы и их смеси При известной
Слайд 2 1. Основные понятия и законы термодинамики 2. Круговые процессы и циклы тепловых
Разделы учебной дисциплины «Теплофизика»
Слайд 3 1. Бендерский Б.Я. Техническая термодинамика и теплопередача. Ижевск: НИЦ РХД, 2007.
Рекомендуемая литература
Слайд 4Термодинамика – наука о закономерностях взаимного преобразования различных видов энергии. Техническая термодинамика
Предмет термодинамики
Слайд 5Термодинамическая система
Термодинамическая система – материальное тело (или совокупность тел), способное (способных)
Изолированная система с течением времени всегда переходит в состояние термодинамического равновесия и никогда самопроизвольно выйти из него не может (первый постулат термодинамики)
Термодинамическая система, обменивающаяся веществом с другими системами, называется открытой.
Термодинамическая система, которая не может обмениваться теплотой с другими системами называется теплоизолированной или адиабатно-изолированной.
Слайд 6Термодинамическая система
Различают гомогенные и гетерогенные системы.
Гетерогенная система – макроскопически неоднородная физико-химическая
Слайд 7Экстенсивные параметры – характеризуют систему как целое. Это масса и пропорциональные
Интенсивные параметры – не зависят от массы и могут принимать вполне определенные значения в каждой точке системы.
Основные параметры: давление P, температура Т, объем V. Также параметрами являются внутренняя энергия U, энтальпия Н, энтропия S и др.
Параметры состояния
Слайд 8Температура
Температура – мера нагретости тела. С т.з. молекулярно-кинетической теории, температура –
где k – постоянная Больцмана 1.380622 10-23 Дж/К
К – по Кельвину, С – по Цельсию, R – по Реомюру, F – по Фаренгейту
Слайд 9Давление
Давление представляет собой средний результат силового воздействия молекул на стенки оболочки,
В соответствии с молекулярно кинетической теорией газа давление определяется как
Где n – число молекул в единице объема, m – масса молекулы, с – средняя скорость движения молекул.
1 Па = 1 Н/м2
1 бар = 105 Па
Слайд 10Удельный объем
Удельный объем – объем единицы массы вещества.
Обратная величина – плотность
Любой из параметров состояния системы является функцией других ее параметров:
М – масса рабочего тела, V – объем
Термодинамические параметры v, p, и Т в равновесном состоянии связаны зависимостью f (p, v, T) =0
Слайд 11Уравнение состояния
Функциональная зависимость между параметрами простой термодинамической системы – давлением, объемом,
где каждая из переменных является функцией двух других
Идеальный газ – система, в которой можно пренебречь объемом молекул и силами их взаимного притяжения.
Из уравнения состояния получим приращение давления:
Слайд 12Уравнение состояния
Связь между коэффициентом объемного расширения α при постоянном давлении, изотермическим
Пользуясь этими соотношениями и уравнением состояния, получаем зависимость
Это соотношение справедливо при любом конкретном виде функциональной связи объема, давления и температуры в уравнении состояния
Слайд 13Уравнение Ван дер Ваальса
Для одного моля имеет вид:
При p ≥ a/v2
Поправка b учитывает объем, занимаемый молекулами газа реального газа; так называемое «мертвое пространство», куда не могут проникнуть молекулы реального газа при движении, т.е. объем зазоров между молекулами при их плотной упаковки.
Таким образом:
Слайд 14Уравнение Ван дер Ваальса
Поправка к давлению a/v2 учитывает силы взаимодействия между
где ρ – плотность газа.
Таким образом, полное давление складывается из внешнего и внутреннего давлений:
Слайд 15
К – критическая точка с критическими параметрами рабочего тела pk, Tk
На участке ВСА изотермы Т1 давление растет с увеличением объема
(dP/dV) > 0.
Данное состояние неустойчиво, поскольку здесь должны усиливаться малейшие флуктуации плотности.
Поэтому область ВСА не может устойчиво существовать.
Слайд 16Термодинамические процессы
Изменение состояния рабочего тела под воздействием окружающей среды в термодинамике
Термодинамические процессы, происходящие при неизменном значении какого-либо параметра состояния, называются изопроцессами.
Слайд 18Термодинамические процессы
Основным свойством равновесного термодинамического процесса является обратимость.
Обратимым называется процесс, при
При обратимом процессе работа, совершаемая системой при переходе из начального состояния в конечное – максимальна, а работа, затрачиваемая на обратный перевод – минимальна.
Все реальные процессы протекают с конечной скоростью и не являются равновесными или обратимыми.
Слайд 19Термодинамические процессы
Замкнутый круговой процесс (цикл) в координатах P-V
Рассматривают квазистатические (как бы
Основной интерес представляют замкнутые (круговые) процессы, когда система проходит через ряд равновесных состояний и возвращается в первоначальное
Слайд 20Идеальные газы и их смеси
Уравнение состояния идеального газа Клапейрона
При нормальных условиях:
R – удельная газовая постоянная, Дж/(кг*К)
Для произвольной массы М:
Уравнение Менделееева – Клапейрона для 1 кмоль:
Rμ – универсальная газовая постоянная, Дж/(кмоль*К)
Слайд 21Идеальные газы и их смеси
Для любого газа:
RСМ – газовая постоянная смеси
μСМ
Молекулярная масса некоторых газов
Для газовой смеси массой М уравнение состояния имеет вид:
Слайд 22Идеальные газы и их смеси
Газовая смесь может быть задана массовыми долями
i = 1.. n
Аналогично для объема:
Газовая постоянная:
Слайд 23Идеальные газы и их смеси
При известной газовой постоянной RСМ:
Давление газовой смеси
Парциальное давление – давление, которое имеет газ, занимающий весь объем смеси при той же температуре.
Связь между массовыми и объемными долями