- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сверхпроводимость и теория Гинсбурга-Ландау презентация
Содержание
- 1. Сверхпроводимость и теория Гинсбурга-Ландау
- 2. ЭКСПЕРИМЕНТАЛЬНОЕ ОТКРЫТИЕ 1908 год – получен жидкий
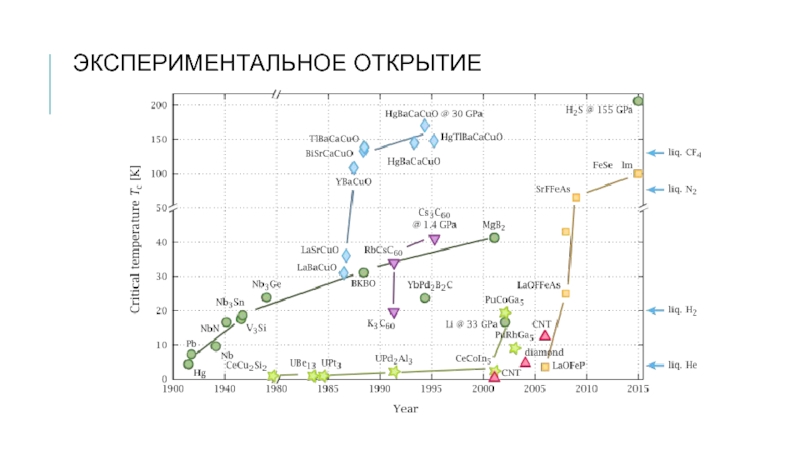
- 3. ЭКСПЕРИМЕНТАЛЬНОЕ ОТКРЫТИЕ
- 4. ВЫСОКОТЕМПЕРАТУРНАЯ СВЕРХПРОВОДИМОСТЬ Первое соединение из класса высокотемпературных
- 5. ЭФФЕКТ МЕЙСНЕРА В. Мейснер и Р. Оксенфельд, 1933 год
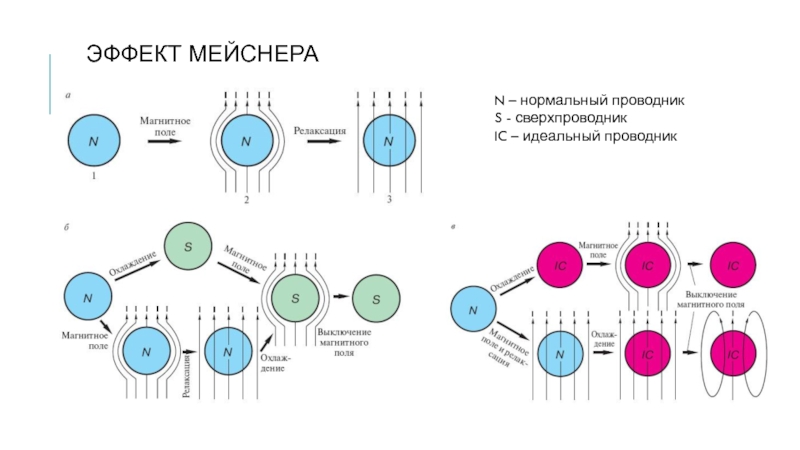
- 6. ЭФФЕКТ МЕЙСНЕРА N – нормальный проводник S - сверхпроводник IC – идеальный проводник
- 7. СВЕРХПРОВОДНИКИ II РОДА В январе 1914 года
- 8. ТЕОРЕТИЧЕСКОЕ ОПИСАНИЕ 1935 – уравнение Лондонов 1950
- 9. ТЕОРИЯ КРИТИЧЕСКИХ ЯВЛЕНИЙ ГИНЗБУРГА-ЛАНДАУ Фазовые переходы второго
- 10. ФЕНОМЕНОЛОГИЧЕСКАЯ ТЕОРИЯ Ландау и Гинзбург предположили общий
- 11. ТЕОРИЯ ГИНЗБУРГА-ЛАНДАУ ДЛЯ СВЕРХПРОВОДИМОСТИ Переход в сверхпроводящее
- 12. ТЕОРИЯ ГИНЗБУРГА-ЛАНДАУ ДЛЯ СВЕРХПРОВОДИМОСТИ Из условия минимума
- 13. ТЕОРИЯ ГИНЗБУРГА-ЛАНДАУ ДЛЯ СВЕРХПРОВОДИМОСТИ Длина когерентности:
- 14. ТЕОРИЯ ГИНЗБУРГА-ЛАНДАУ Из общего вида свободной энергии
- 15. СОЗДАНИЕ КВАНТОВОЙ ТЕОРИИ Поиски устойчивых бозе-подобных комплексов
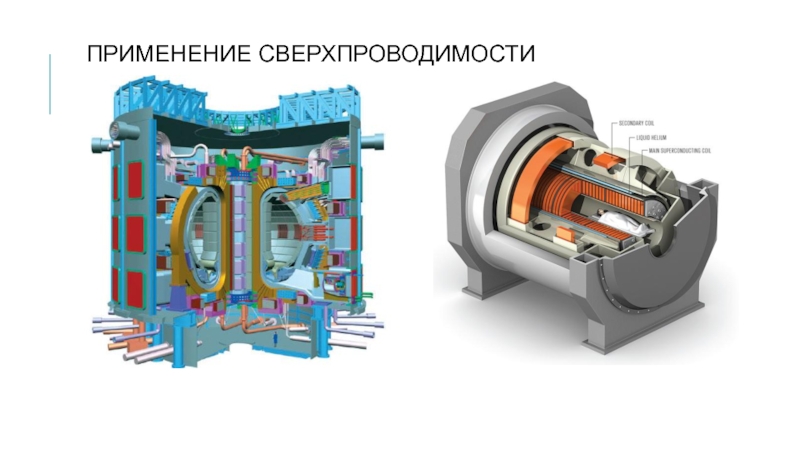
- 16. ПРИМЕНЕНИЕ СВЕРХПРОВОДИМОСТИ Магниты: Сверхпроводящие провода:
- 17. ПРИМЕНЕНИЕ СВЕРХПРОВОДИМОСТИ Магниты:
- 18. БКШ НЕ БУДЕТ Спасибо за внимание!
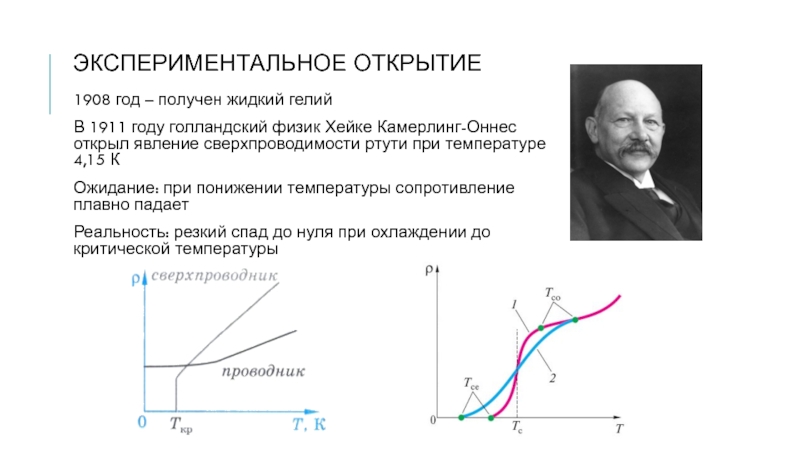
Слайд 2ЭКСПЕРИМЕНТАЛЬНОЕ ОТКРЫТИЕ
1908 год – получен жидкий гелий
В 1911 году голландский физик Хейке Камерлинг-Оннес
открыл явление сверхпроводимости ртути при температуре 4,15 К
Ожидание: при понижении температуры сопротивление плавно падает
Реальность: резкий спад до нуля при охлаждении до критической температуры
Ожидание: при понижении температуры сопротивление плавно падает
Реальность: резкий спад до нуля при охлаждении до критической температуры
Слайд 4ВЫСОКОТЕМПЕРАТУРНАЯ СВЕРХПРОВОДИМОСТЬ
Первое соединение из класса высокотемпературных сверхпроводящих купратов La2-xBaxCuO4 открыли Карл Мюллер и Георг
Беднорц в 1986 г. За это открытие в 1987 г. им была немедленно присуждена Нобелевская премия.
В настоящее время рекордным значением критической температуры Tc =135 K (под давлением Tc=165 K, −109 °C) обладает вещество HgBa2Ca2Cu3O8+x, открытое в 1993 г. С. Н. Путилиным и Е. В. Антиповым из МГУ.
В настоящее время рекордным значением критической температуры Tc =135 K (под давлением Tc=165 K, −109 °C) обладает вещество HgBa2Ca2Cu3O8+x, открытое в 1993 г. С. Н. Путилиным и Е. В. Антиповым из МГУ.
Слайд 7СВЕРХПРОВОДНИКИ II РОДА
В январе 1914 года было показано, что сверхпроводимость разрушается
сильным магнитным полем.
1935 – Лев Шубников открыл сверхпроводники II рода
1935 – Лев Шубников открыл сверхпроводники II рода
Слайд 8ТЕОРЕТИЧЕСКОЕ ОПИСАНИЕ
1935 – уравнение Лондонов
1950 – теория Гинзбурга-Ландау
1957 – квантовая теория
БКШ, теория Бардина-Купера-Шриффера, Нобелевская премия 1972 года
1958 – Н.Н. Боголюбов, канонические преобразования
1962 – эффект Джосефсона, Нобелевская премия 1973 года
Вихри Абрикосова - В.Л. Гинзбург, А.А. Абрикосов, Нобелевская премия 2003 года.
1958 – Н.Н. Боголюбов, канонические преобразования
1962 – эффект Джосефсона, Нобелевская премия 1973 года
Вихри Абрикосова - В.Л. Гинзбург, А.А. Абрикосов, Нобелевская премия 2003 года.
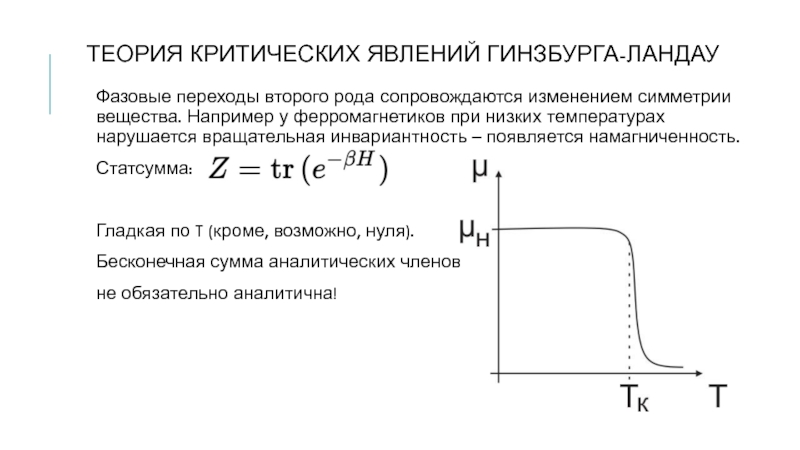
Слайд 9ТЕОРИЯ КРИТИЧЕСКИХ ЯВЛЕНИЙ ГИНЗБУРГА-ЛАНДАУ
Фазовые переходы второго рода сопровождаются изменением симметрии вещества.
Например у ферромагнетиков при низких температурах нарушается вращательная инвариантность – появляется намагниченность.
Статсумма:
Гладкая по T (кроме, возможно, нуля).
Бесконечная сумма аналитических членов
не обязательно аналитична!
Статсумма:
Гладкая по T (кроме, возможно, нуля).
Бесконечная сумма аналитических членов
не обязательно аналитична!
Слайд 10ФЕНОМЕНОЛОГИЧЕСКАЯ ТЕОРИЯ
Ландау и Гинзбург предположили общий вид свободной энергии в виде
полинома:
где a, b – гладкие функции от T, и можно ожидать a = a1(T-TК).
Спонтанное нарушение симметрии –
причина успеха нашей вселенной!
(см. поле Хиггса)
где a, b – гладкие функции от T, и можно ожидать a = a1(T-TК).
Спонтанное нарушение симметрии –
причина успеха нашей вселенной!
(см. поле Хиггса)
Слайд 11ТЕОРИЯ ГИНЗБУРГА-ЛАНДАУ ДЛЯ СВЕРХПРОВОДИМОСТИ
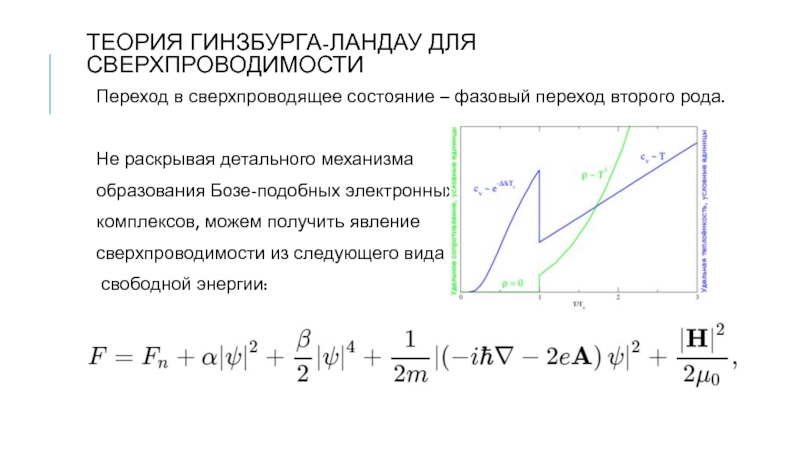
Переход в сверхпроводящее состояние – фазовый переход второго
рода.
Не раскрывая детального механизма
образования Бозе-подобных электронных
комплексов, можем получить явление
сверхпроводимости из следующего вида
свободной энергии:
Не раскрывая детального механизма
образования Бозе-подобных электронных
комплексов, можем получить явление
сверхпроводимости из следующего вида
свободной энергии:
Слайд 12ТЕОРИЯ ГИНЗБУРГА-ЛАНДАУ ДЛЯ СВЕРХПРОВОДИМОСТИ
Из условия минимума свободной энергии следуют уравнения Гинзбурга-Ландау
для
бозонного и электромагнитного поля :
Из них находятся лондонская длина проникновения магнитного поля и длина когерентности.
Из них находятся лондонская длина проникновения магнитного поля и длина когерентности.
Слайд 13ТЕОРИЯ ГИНЗБУРГА-ЛАНДАУ ДЛЯ СВЕРХПРОВОДИМОСТИ
Длина когерентности: , «размер куперовской пары»
Длина
проникновения магнитного поля: ,
Параметр Гинзбурга-Ландау κ = λ/ξ , для сверхпроводников II типа κ > 1/√2.
Параметр Гинзбурга-Ландау κ = λ/ξ , для сверхпроводников II типа κ > 1/√2.
Слайд 14ТЕОРИЯ ГИНЗБУРГА-ЛАНДАУ
Из общего вида свободной энергии рассчитали Лондоновскую длину, длину когерентности,
получили, что сверхпроводники бывают первого и второго рода (с неполным эффектом Мейснера) и получили как следствие вихри Абрикосова во вторых.
Есть повод для гордости!
Есть повод для гордости!
Слайд 15СОЗДАНИЕ КВАНТОВОЙ ТЕОРИИ
Поиски устойчивых бозе-подобных комплексов для описания сверхпроводимости –
1956
– Куперовская пара
1957 – БКШ, квантовая теория.
1957 – БКШ, квантовая теория.