- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Строительная акустика. Звуковые волны. Спектры. Звуковое давление. Интенсивность звука презентация
Содержание
- 1. Строительная акустика. Звуковые волны. Спектры. Звуковое давление. Интенсивность звука
- 2. moodle.spbgasu.ru
- 3. 1 Лекция - тезисы Основные понятия Звуковые волны Спектры Звуковое давление Интенсивность звука
- 4. Литература Архитектурная физика / Под ред
- 5. Нормативные документы СНИП 23-03-2003 «Защита
- 6. Архитектурно-строительная акустика Основной задачей архитектурной акустики
- 7. Свободные (собственные) колебания Совершаются за счёт первоначально
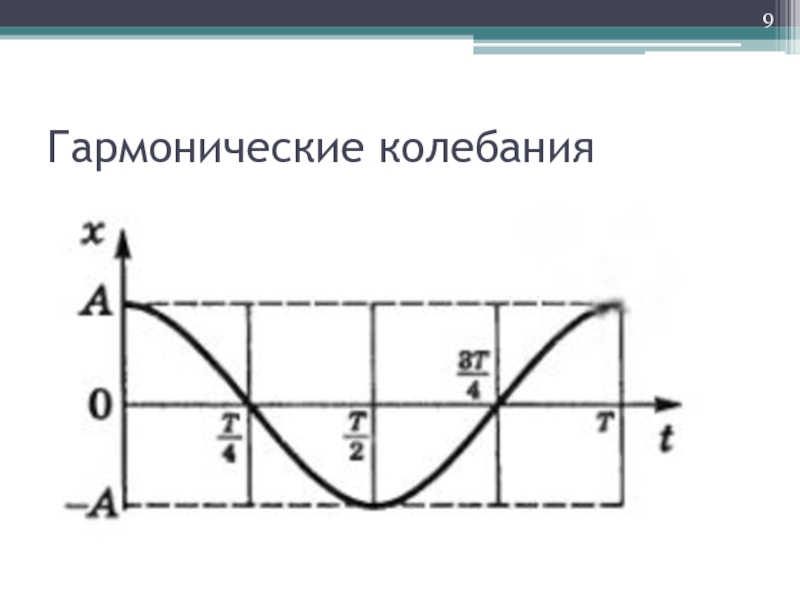
- 8. Гармонические колебания
- 9. Гармонические колебания
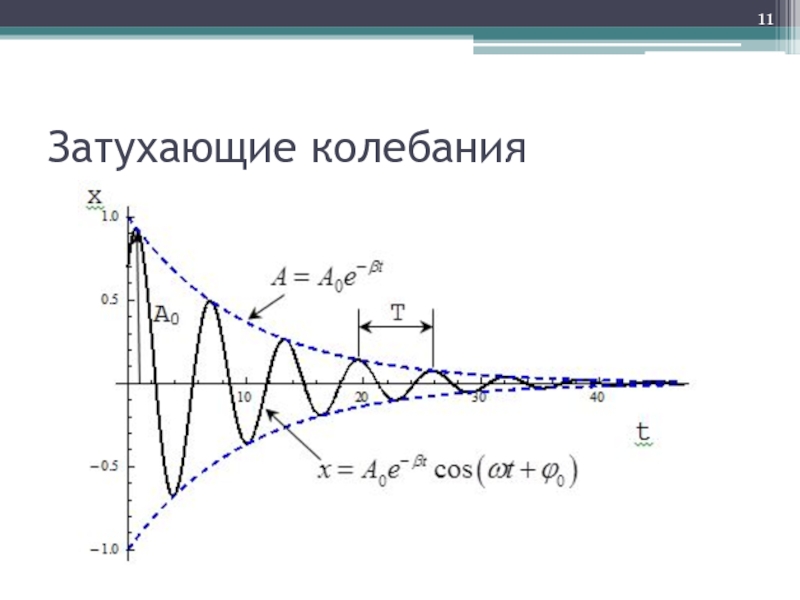
- 10. Затухающие колебания Колебания, амплитуда которых с течением времени уменьшается из-за потерь энергии реальной колебательной системой
- 11. Затухающие колебания
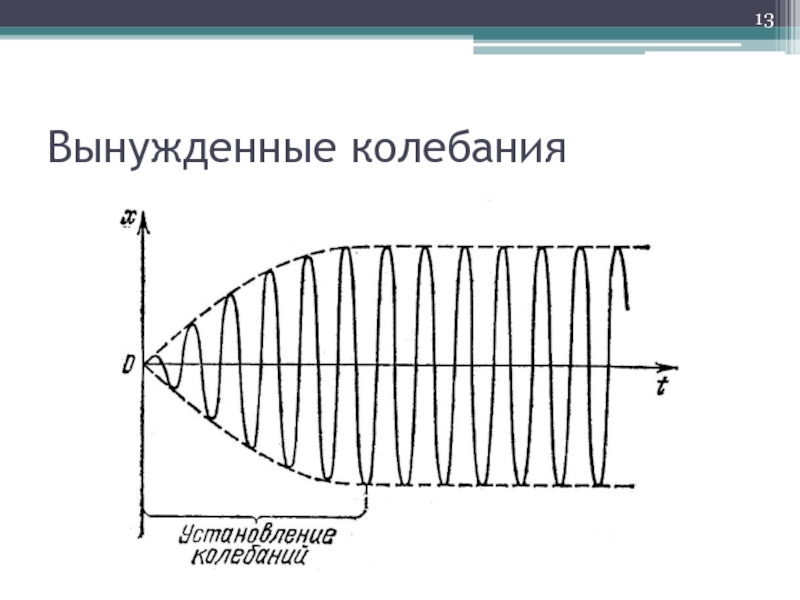
- 12. Вынужденные колебания
- 13. Вынужденные колебания
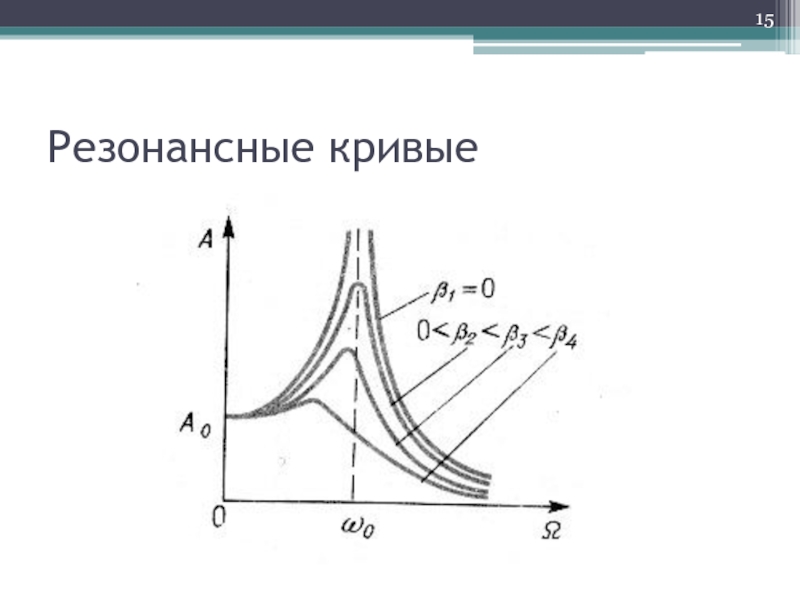
- 14. Резонанс Явление резкого возрастания амплитуды вынужденных колебаний
- 15. Резонансные кривые
- 16. Основные понятия. Звуковые волны. Звук – это
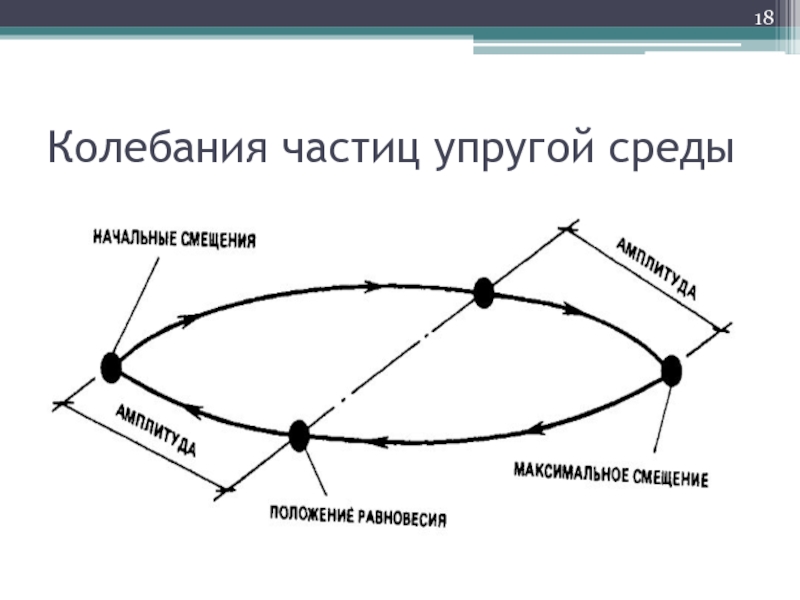
- 18. Колебания частиц упругой среды
- 19. Фронтом звуковой волны называют поверхность, проходящую через
- 21. Гармоническая волна или синусоидальная волна Упругая волна
- 23. Длина волны Расстояние, измеренное вдоль направления распространения
- 24. Волновая поверхность (фронт волны) Геометрическое место точек,
- 25. Волна называется Плоской, если её волновые поверхности
- 27. Уравнение бегущей волны Источник: точка,
- 28. Уравнение бегущей волны Плоская волна Сферическая волна
- 29. Волновое уравнение (в общем случае в однородной
- 30. Звуковые волны (звук) упругие волны, т.е. механические
- 31. Частотные диапазоны Инфразвук Звук Ультразвук Диапазон слышимости
- 32. Волна характеризуется Амплитудой Частотой Формой
- 33. Амплитуда
- 34. Частота
- 35. Форма волны Синусоидальная звуковая волна – чистый тон Несинусоидальная звуковая волна
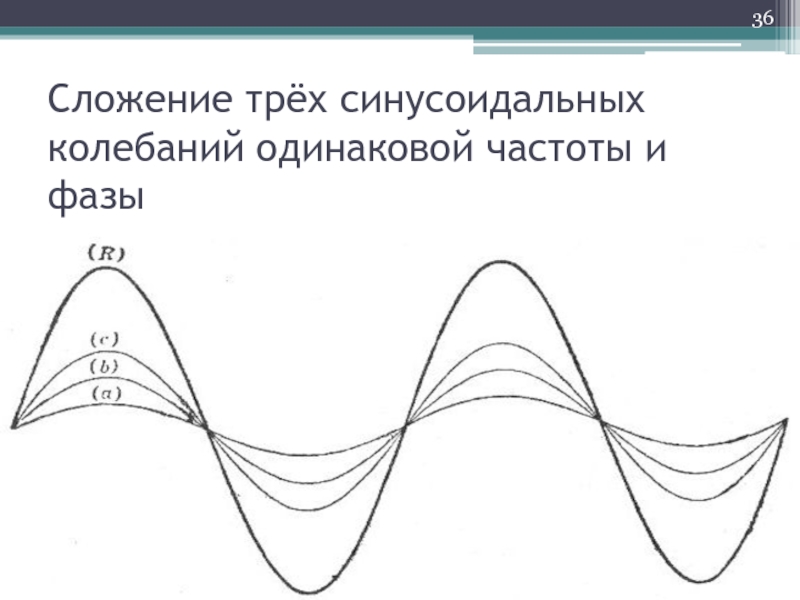
- 36. Сложение трёх синусоидальных колебаний одинаковой частоты и фазы
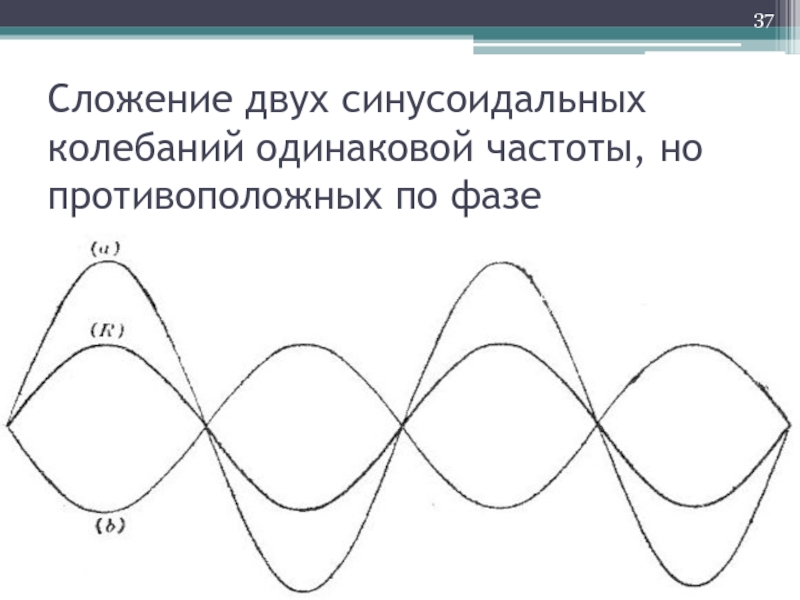
- 37. Сложение двух синусоидальных колебаний одинаковой частоты, но противоположных по фазе
- 38. Сложение трёх синусоидальных колебаний одинаковой частоты и амплитуды, но несовпадающих по фазе
- 39. Сложение двух синусоидальных колебаний с близкими частотами (биения)
- 40. Сложение трёх синусоидальных колебаний с кратными частотами (1:2:3) (на примере скрипичного тона)
- 41. Форма волны Тон: Звуковые колебания синусоидальной формы.
- 42. Восприятие звука в зависимости от свойств волны
- 44. Частотный спектр (или частотная характеристика)
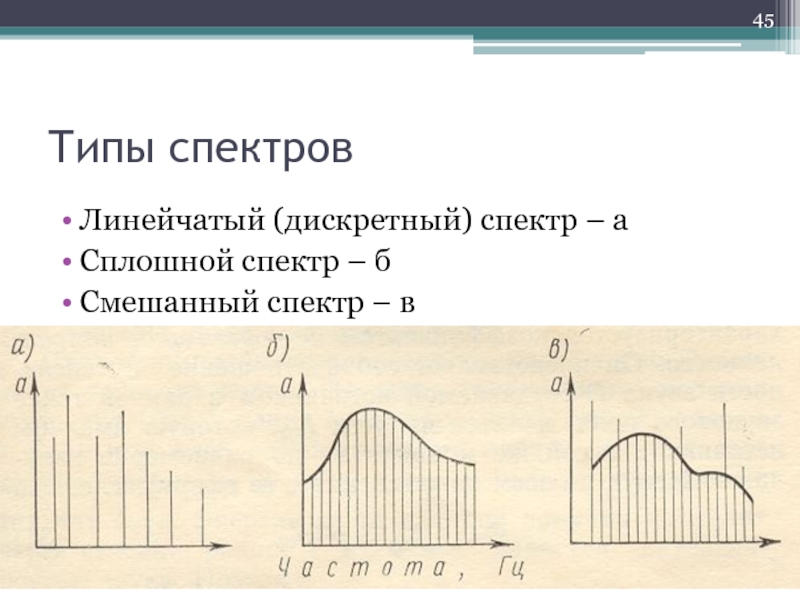
- 45. Типы спектров Линейчатый (дискретный) спектр – а
- 46. Типы спектров Линейчатый дискретный спектр периодические колебания
- 47. Белый шум - равномерное распределение энергии в звуковом диапазоне частот
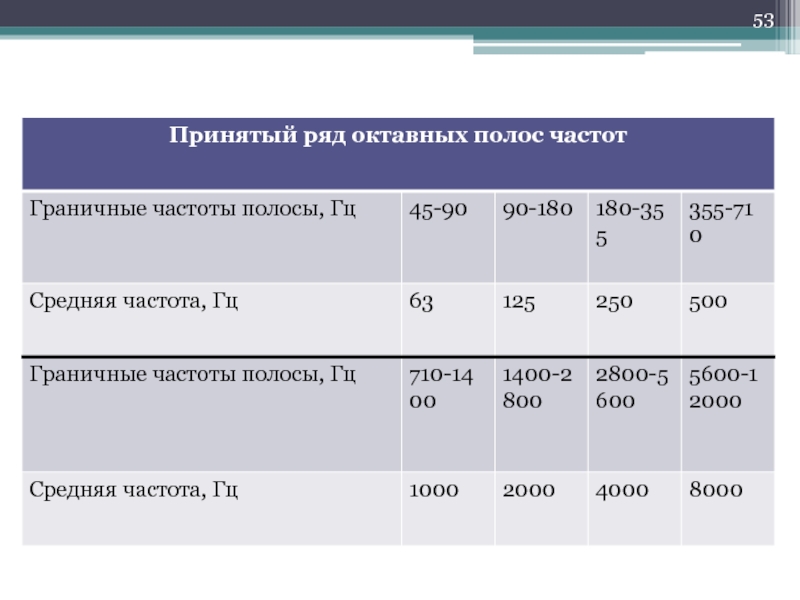
- 49. Октава полоса частот (от f1 до f2),
- 50. Частоты в октавных интервалах
- 51. Музыкальные интервалы Октава Квинта Кварта Большая терция
- 52. Музыкальные интервалы
- 55. Продольная волна направление колебаний частиц среды совпадает
- 56. Поперечная волна частицы среды колеблются, оставаясь в
- 57. Упругие свойства среды характеризуются одной или двумя
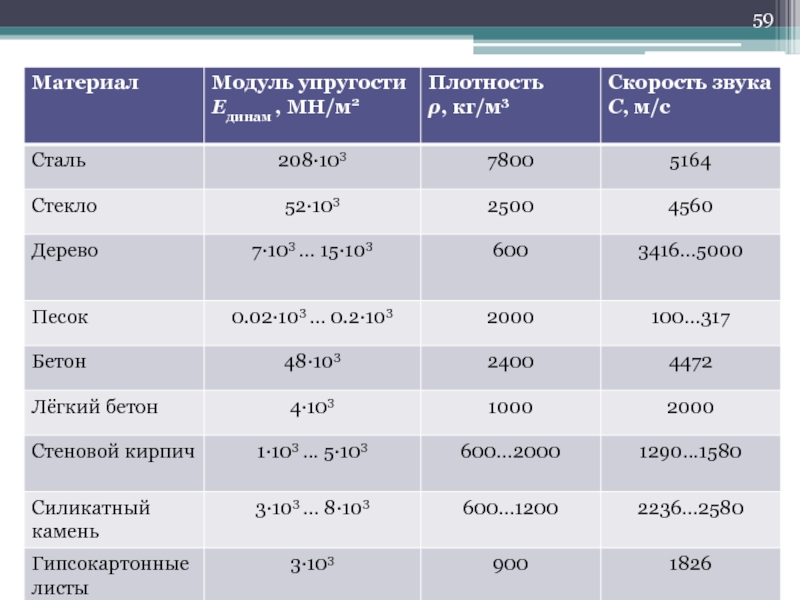
- 58. Скорость распространения Продольной волны в однородной газообразной
- 60. Скорость распространения звуковой волны в газе
Слайд 4Литература
Архитектурная физика / Под ред Н.В. Оболенского. – М.: Стройиздат, 1997.
– 448 с. [с. 287 - Архитектурная акустика]
Ковригин С.Д. Архитектурно-строительная акустика. – М.: Высш. шк., 1980. – 184 с.
Ковригин С.Д. Архитектурно-строительная акустика. – М.: Высш. шк., 1980. – 184 с.
Слайд 5Нормативные документы
СНИП 23-03-2003
«Защита от шума»
СП 23-103-2003
«Проектирование
звукоизоляции ограждающих конструкций жилых и общественных зданий»
Слайд 6
Архитектурно-строительная акустика
Основной задачей архитектурной акустики является исследование условий, определяющих слышимость звука
и музыки в помещениях, и разработка архитектурных планировочных и конструктивных решений, обеспечивающих оптимальные условия слухового восприятия.
А так же, подавление шума (обеспечение звукоизоляции и шумозащиты)
А так же, подавление шума (обеспечение звукоизоляции и шумозащиты)
Слайд 7Свободные (собственные) колебания
Совершаются за счёт первоначально сообщённой энергии при последующем отсутствии
внешних воздействий на систему, совершающую колебания
Слайд 8Гармонические колебания
- амплитуда колебания
- собственная частота колебаний
- начальная фаза
- собственная частота колебаний
- начальная фаза
Слайд 10Затухающие колебания
Колебания, амплитуда которых с течением времени уменьшается из-за потерь энергии
реальной колебательной системой
Слайд 14Резонанс
Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы
к собственной частоте колебательной системы.
Резонансная частота
Резонансная частота
Слайд 16Основные понятия. Звуковые волны.
Звук – это колебательное движение в любой материальной,
то есть обладающей упругостью и инерционностью среде, вызванное каким-либо источником.
Звуковой волной называют процесс распространения колебательного движения в среде.
Звуковой волной называют процесс распространения колебательного движения в среде.
Слайд 19Фронтом звуковой волны называют поверхность, проходящую через частицы среды, совершающие колебания
в одной и той же фазе. Направление распространения звука в каждой точке фронта является нормалью к его поверхности.
Слайд 21Гармоническая волна или синусоидальная волна
Упругая волна называется гармонической, если соответствующие ей
колебания частиц среды являются гармоническими.
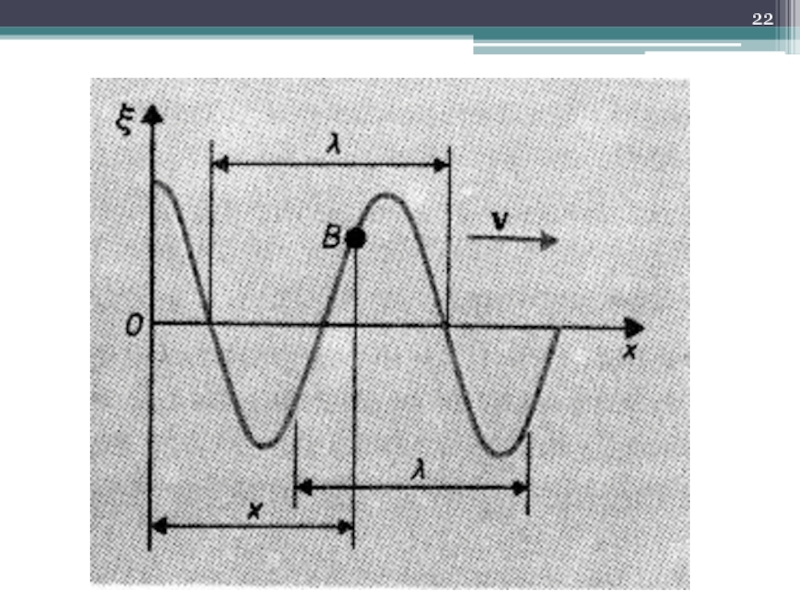
Слайд 23Длина волны
Расстояние, измеренное вдоль направления распространения волны, между ближайшими частицами, колеблющимися
в одинаковой фазе (разность фаз их колебаний равна 2 π)
Расстояние, за которое распространяется волна за время равное периоду колебаний
Расстояние, за которое распространяется волна за время равное периоду колебаний
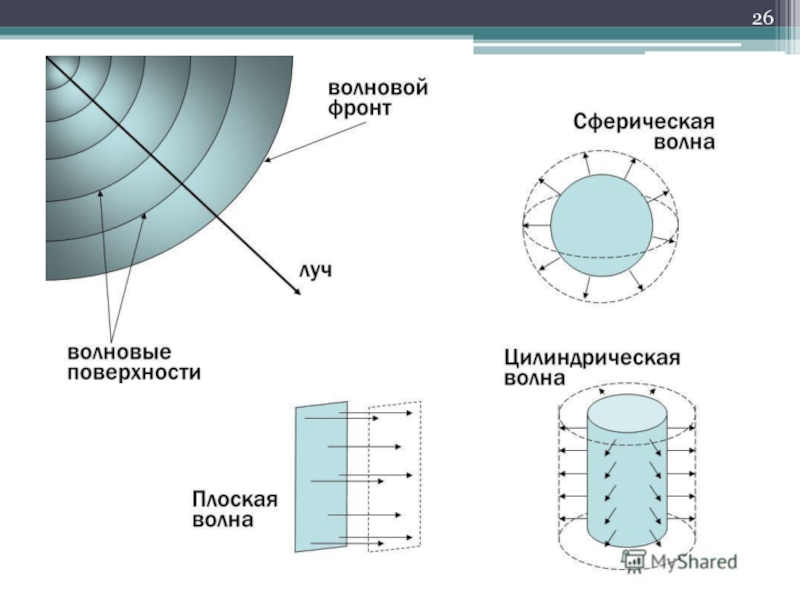
Слайд 24Волновая поверхность (фронт волны)
Геометрическое место точек, в которых фаза колебаний имеет
одно и то же значение
Направление распространения волны в каждой точке волновой поверхности является нормалью к ней
Направление распространения волны в каждой точке волновой поверхности является нормалью к ней
Слайд 25Волна называется
Плоской, если её волновые поверхности представляют совокупность плоскостей, параллельных друг
другу
Сферической (шаровой), если её волновые поверхности имеют вид концентрических сфер
Цилиндрической, если её волновые поверхности имеют вид боковых поверхностей цилиндра
Сферической (шаровой), если её волновые поверхности имеют вид концентрических сфер
Цилиндрической, если её волновые поверхности имеют вид боковых поверхностей цилиндра
Слайд 27Уравнение бегущей волны
Источник:
точка, расположенная на расстоянии x от источника колебаний в
момент времени t:
- время, необходимое для
прохождения волной расстояния x
- время, необходимое для
прохождения волной расстояния x
Слайд 30Звуковые волны (звук)
упругие волны, т.е. механические возмущения, распространяющиеся в упругой среде,
вызывающие у человека звуковые ощущения
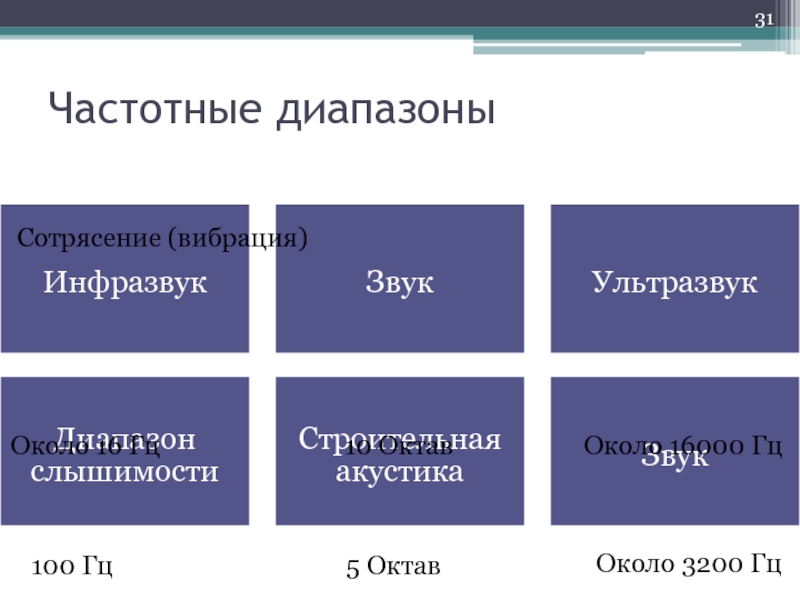
Слайд 31Частотные диапазоны
Инфразвук
Звук
Ультразвук
Диапазон слышимости
Строительная акустика
Звук
Около 16 Гц
10 Октав
Около 16000 Гц
100 Гц
5 Октав
Около
3200 Гц
Сотрясение (вибрация)
Слайд 38Сложение трёх синусоидальных колебаний одинаковой частоты и амплитуды, но несовпадающих по
фазе
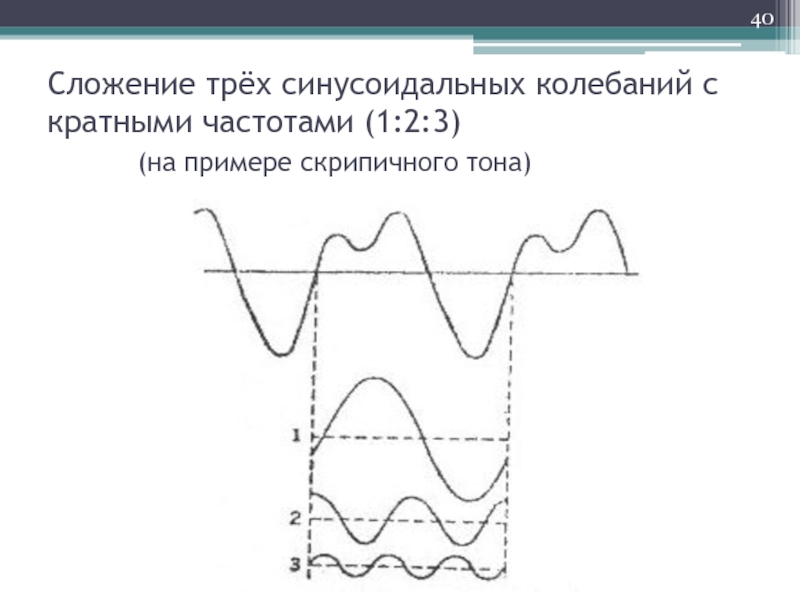
Слайд 40Сложение трёх синусоидальных колебаний с кратными частотами (1:2:3) (на
примере скрипичного тона)
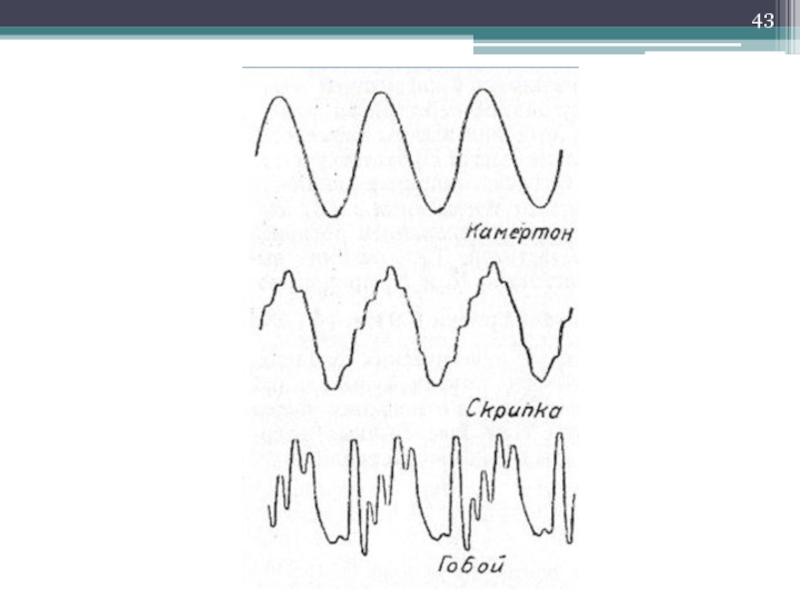
Слайд 41Форма волны
Тон: Звуковые колебания синусоидальной формы.
Звучание: Наложение многих тонов.
Шум: Нерегулярные колебания
без закономерной зависимости.
Громкий резкий короткий звук: Кратковременный, очень сильный быстро кончающийся звуковой сигнал.
Громкий резкий короткий звук: Кратковременный, очень сильный быстро кончающийся звуковой сигнал.
Слайд 42Восприятие звука в зависимости от свойств волны
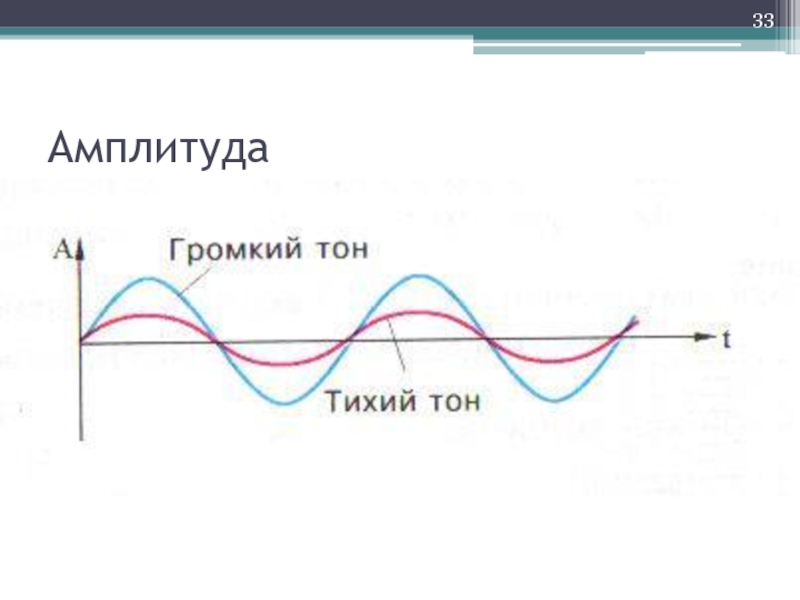
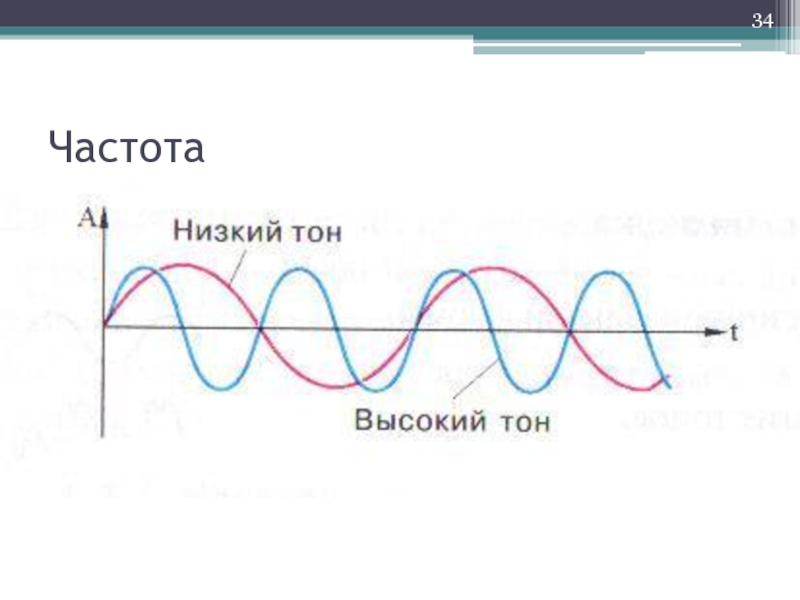
Частота – определяет высоту тона
Амплитуда
– определяет громкость
Форма волны – определяет окраску звучания
Форма волны – определяет окраску звучания
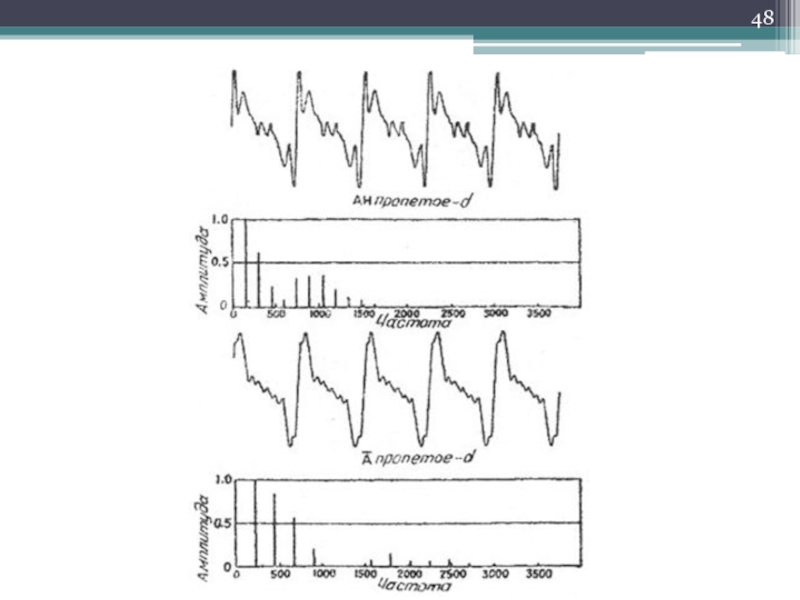
Слайд 44Частотный спектр
(или частотная характеристика)
- Распределение (зависимость) какой-либо физической величины (звуковой энергии,
амплитуды, колебаний и т.п.) от частоты
Слайд 46Типы спектров
Линейчатый дискретный спектр
периодические колебания сложной формы
(представляются суммой синусоидальных колебаний с
различной амплитудой)
Сплошной спектр
непериодические колебания сложной формы
(представляются в виде бесконечно большого числа синусоидальных составляющих)
Смешанный спектр
наложение линейчатого и сплошного спектров
Сплошной спектр
непериодические колебания сложной формы
(представляются в виде бесконечно большого числа синусоидальных составляющих)
Смешанный спектр
наложение линейчатого и сплошного спектров
Слайд 49Октава
полоса частот (от f1 до f2), в которой верхняя частота в
два раза больше нижней
Третьоктавная полоса
За среднюю частоту полосы принимают среднегеометрическую частоту
Третьоктавная полоса
За среднюю частоту полосы принимают среднегеометрическую частоту
Слайд 51Музыкальные интервалы
Октава
Квинта
Кварта
Большая терция
Малая терция
Большая секста
Малая секста
Большая секунда
Малый полутон
2:1
3:2
4:3
6:4
6:5
5:3
8:5
9:8
25:24
Слайд 55Продольная волна
направление колебаний частиц среды совпадает с направлением распространения волны
Продольные волны
связаны с объёмной деформацией.
Могут образовываться и распространяться в любой среде.
Могут образовываться и распространяться в любой среде.
Слайд 56Поперечная волна
частицы среды колеблются, оставаясь в плоскостях, перпендикулярных направлению распространению волны
Поперечные
волны связаны с деформациями сдвига.
Могут образовываться и распространяться только в твёрдых телах
Могут образовываться и распространяться только в твёрдых телах
Слайд 57Упругие свойства среды характеризуются одной или двумя упругими постоянными
K – модуль
объёмной упругости
G – модуль сдвига
G – модуль сдвига
Слайд 58Скорость распространения
Продольной волны в однородной газообразной среде или жидкости
Поперечной волны в
неограниченной изотропной твёрдой среде
Продольной волны в тонком стержне
В пластине
Продольной волны в тонком стержне
В пластине