- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Стеклообразное состояние полимеров. (Лекция 5) презентация
Содержание
- 1. Стеклообразное состояние полимеров. (Лекция 5)
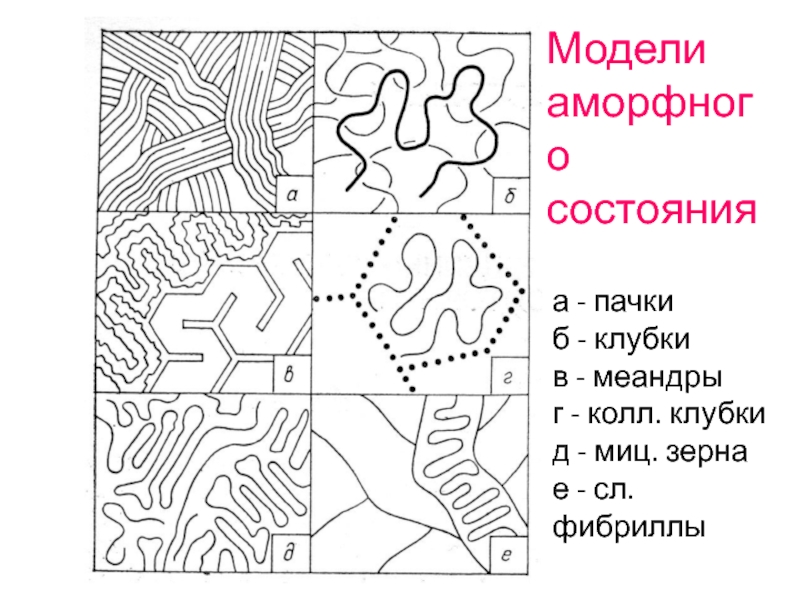
- 2. Модели аморфного состояния а - пачки б
- 7. Переход в стеклообразное состояние не есть фазовый
- 10. Стеклование – фазовый переход? Удовлетворяет критерию Эренфеста:
- 11. Делались неоднократные попытки создать физически простую модель
- 12. Свободный объем
- 13. Свободный объем в жидкостях
- 14. Свободный объем в жидкостях
- 15. Свободный объем в жидкостях
- 16. Свободный объем в жидкостях
- 17. Свободный объем в жидкостях Флуктуационный свободный объем
- 18. Подвижность молекул жидкости Движение частицы осуществляется, когда
- 19. Свободный объем в аморфных полимерах
- 20. Дилато-метричес-кий метод А.А. Тагер. Физико-химия полимеров
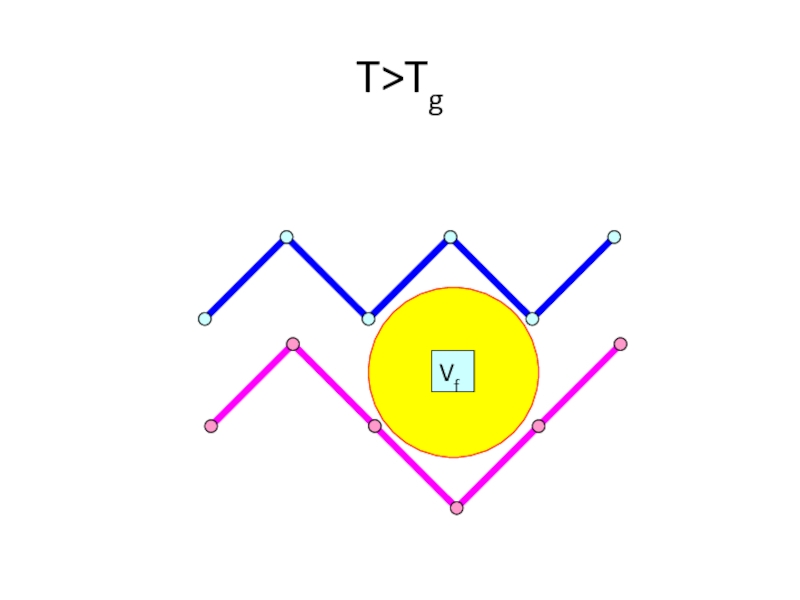
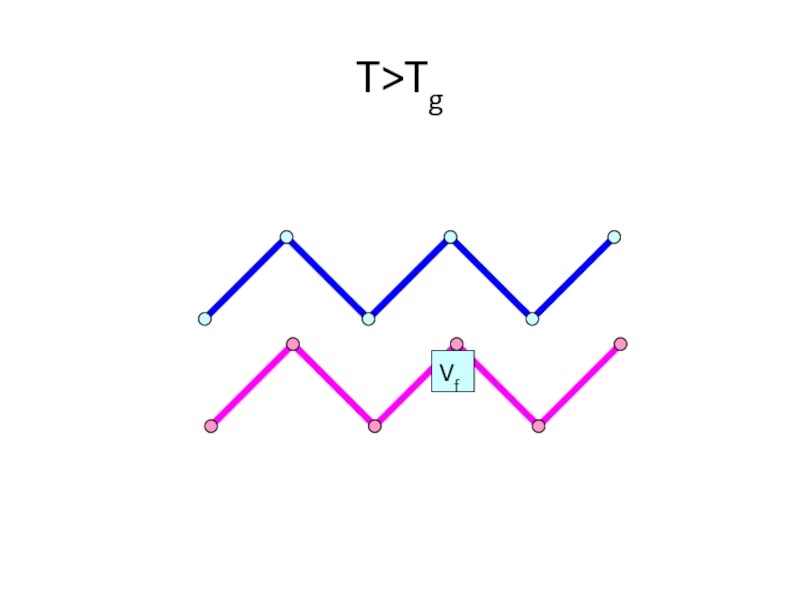
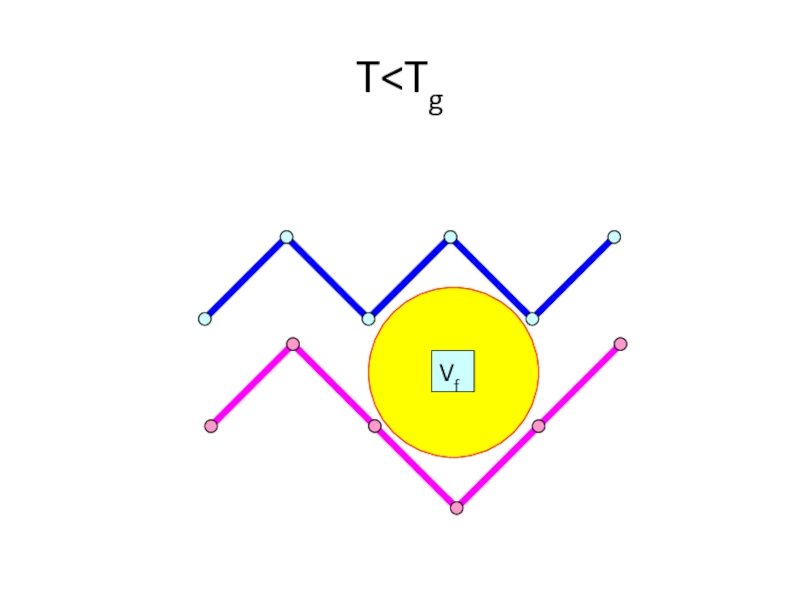
- 21. T>Tg
- 22. T>Tg Vf
- 23. T>Tg Vf
- 24. T
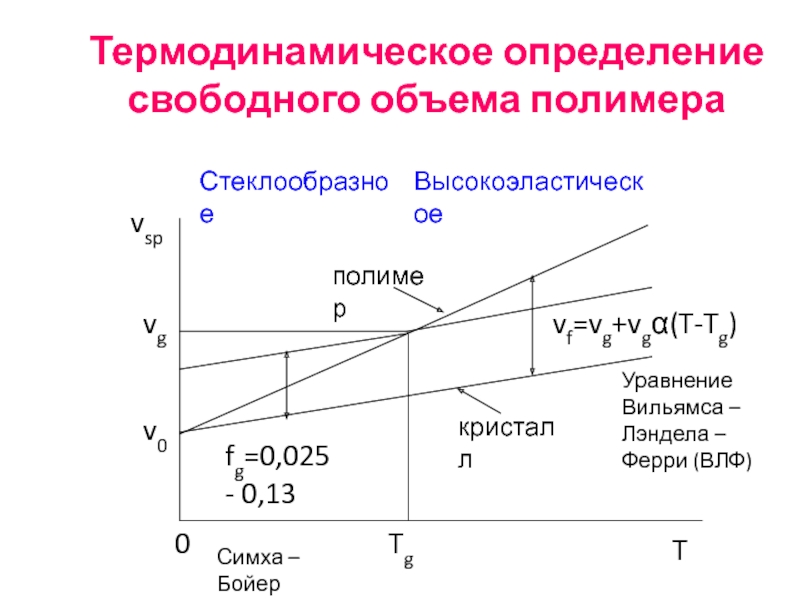
- 25. Термодинамическое определение свободного объема полимера
- 26. Геометрическое определение свободного объема Vf=Vsp-Voc (Vsp=1/ρ);
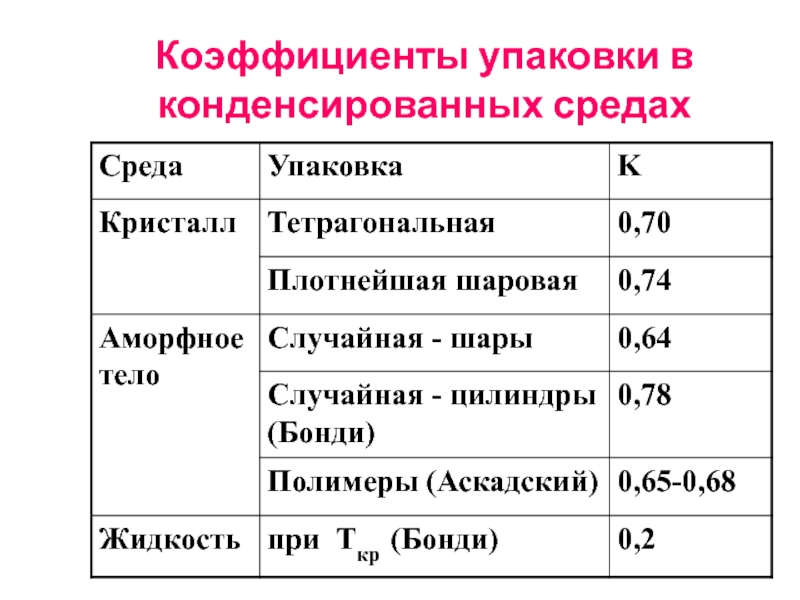
- 27. Коэффициенты упаковки в конденсированных средах
- 28. Свободный объем Vw Vf
- 29. Геометрическое определение свободного объема Vf=Vsp-Voc; f=Vf/Vsp Свободный
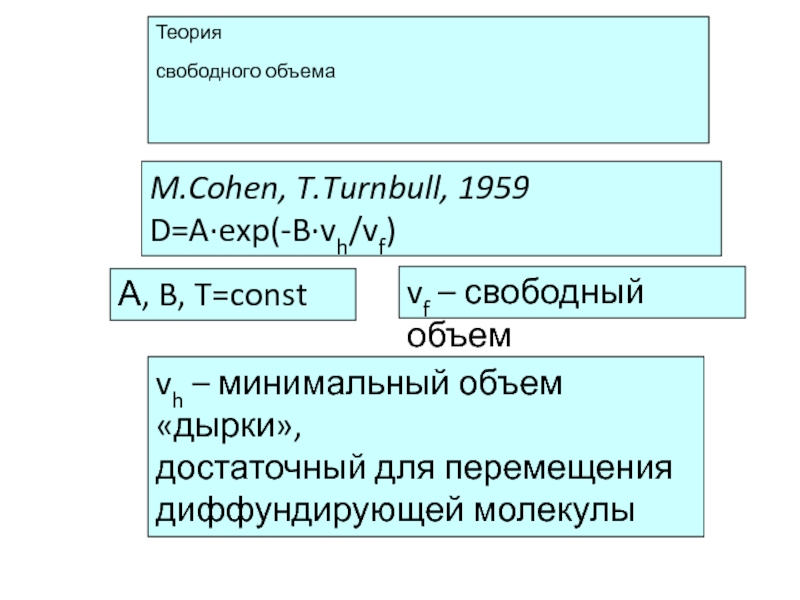
- 30. Теория свободного объема M.Cohen,
- 31. Теория свободного объема M.Cohen,
- 32. Термодинамическое определение свободного объема полимера Стеклообразное
- 33. Тепловое расширение выше Тс определяется изменением свободного
- 34. Эмпирическое соотношение Дулиттла: , где
- 35. Уравнение Вильямса – Лэндела – Ферри (ВЛФ)
- 36. Связь вязкости и скорости сдвига Ньютоновская жидкость Неньютоновская жидкость
- 37. Наибольшая ньютоновская вязкость Вязкость, при которой
- 38. Зависимость наибольшей ньютоновской вязкости от молекулярной массы А.А. Тагер. Физико-химия полимеров Критическая молекулярная масса
- 39. Следствия уравнения Вильямса – Лэндела – Ферри (ВЛФ)
- 40. Для газов: D=AD·exp(-BD/vf) P=D·S D – меняется
- 42. Методы оценки свободного объема. Vf=Vsp-k·Vw Метод
- 43. Корреляции со свободным объемом по Бонди P=A·exp(-B/Vf)
- 44. Корреляции со свободным объемом по Бонди D=A·exp(-B/Vf)
- 45. Связь газопроницаемости и диэлектрических свойств
- 46. Связь коэффициентов диффузии CO2 и механических свойств полиимидов
- 47. Методы оценки свободного объема. Vf=Vsp-k·Vw Метод
- 48. Свободный объем D.N. Theodorou, in:
- 49. Методы оценки свободного объема. Vf=Vsp-k·Vw Метод
- 50. Зондовые методы 1. Методы с переменным размером
- 51. Метод аннигиляции позитронов Спектр времен жизни e+
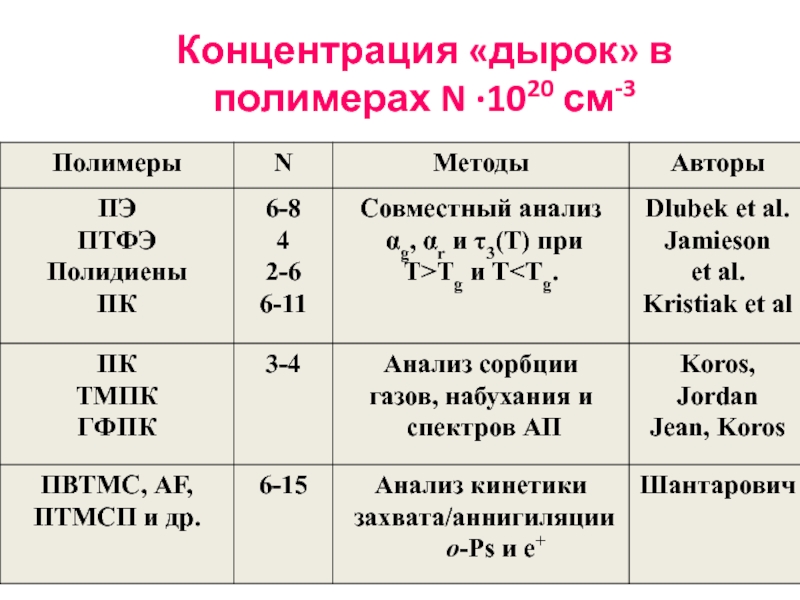
- 52. Средние размеры «дырок» в полимерах
- 53. Концентрация «дырок» в полимерах N ·1020 см-3
- 54. Подвижность «дырок» Изменение характеристик пленки с изменением
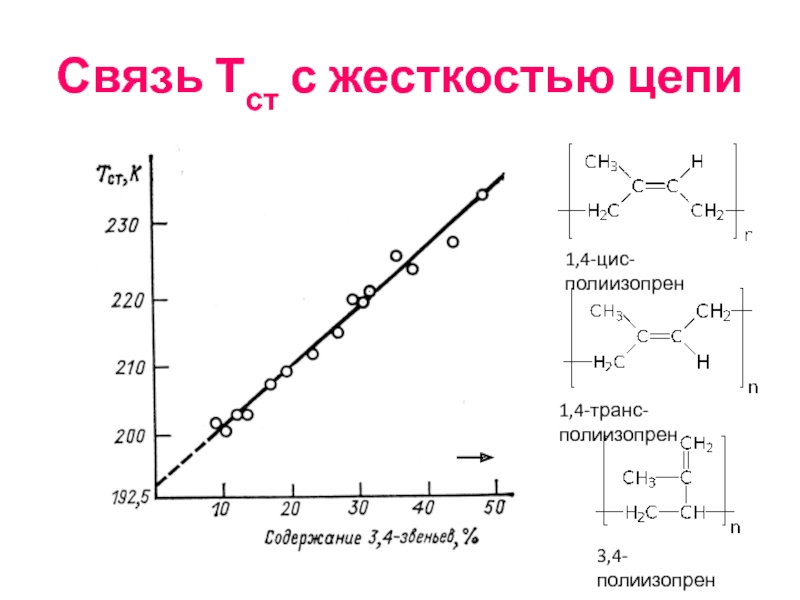
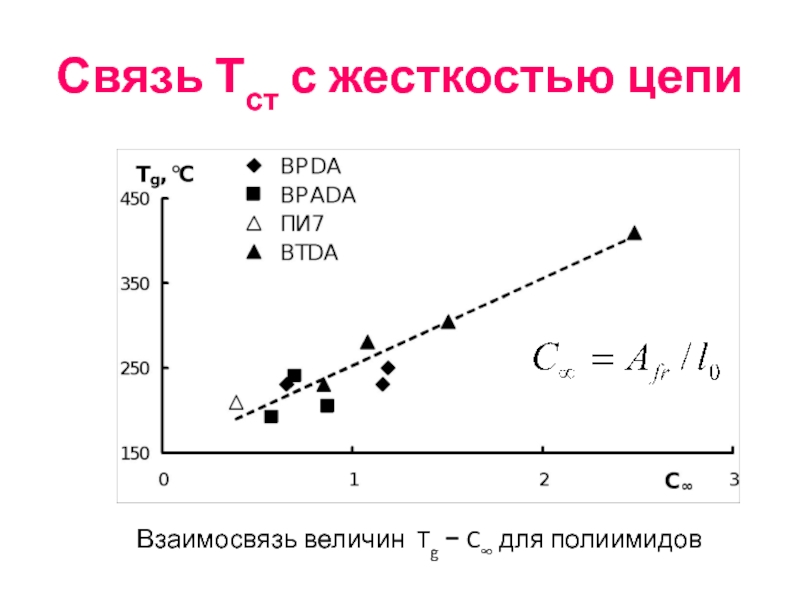
- 56. Связь Тст с жесткостью цепи 1,4-цис-полиизопрен 1,4-транс-полиизопрен 3,4-полиизопрен
- 57. Связь Тст с жесткостью цепи Взаимосвязь величин Tg − C∞ для полиимидов
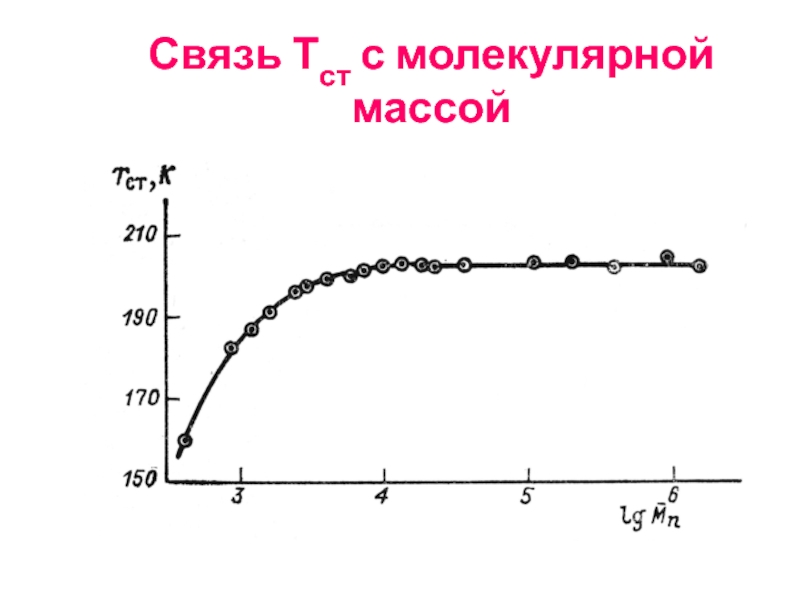
- 58. Связь Тст с молекулярной массой
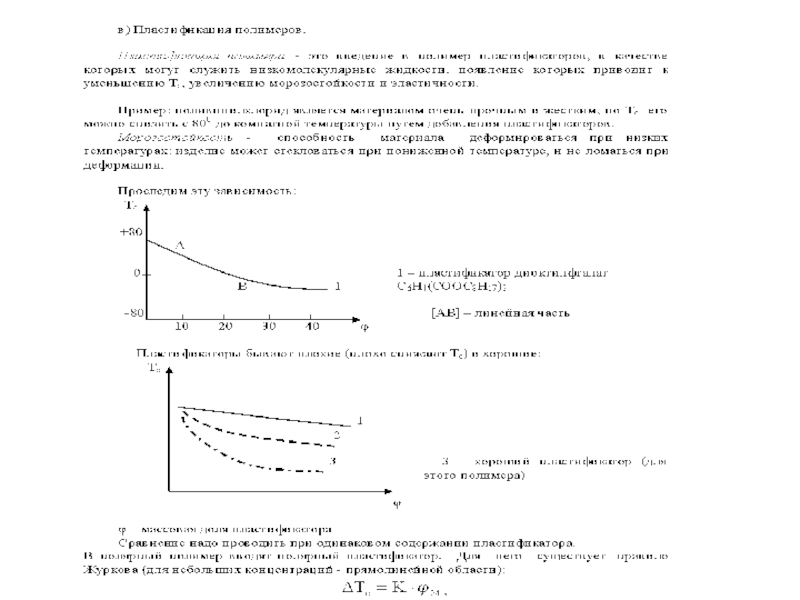
- 59. Пластификация Термодинамическая совместимость с полимером (истинный раствор)
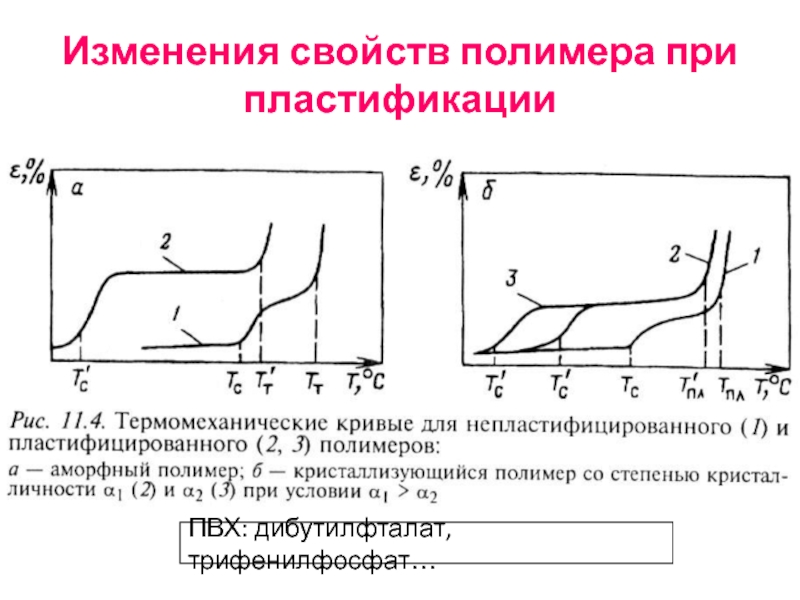
- 61. Изменения свойств полимера при пластификации ПВХ: дибутилфталат, трифенилфосфат…
- 62. Фазовая диаграмма полимер (П) – пластификатор (Пл)
- 63. Антипластификация Термодинамическая совместимость с полимером (истинный раствор)
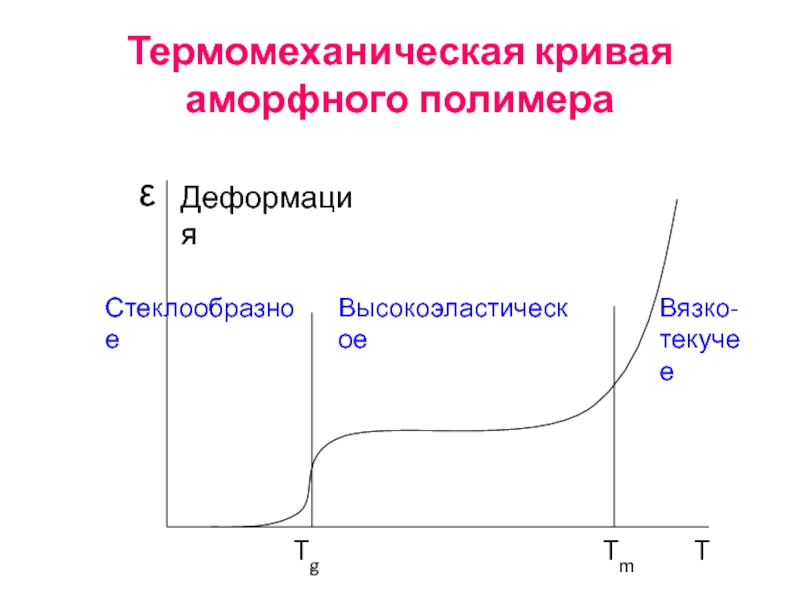
- 64. Термомеханическая кривая аморфного полимера Tg Tm
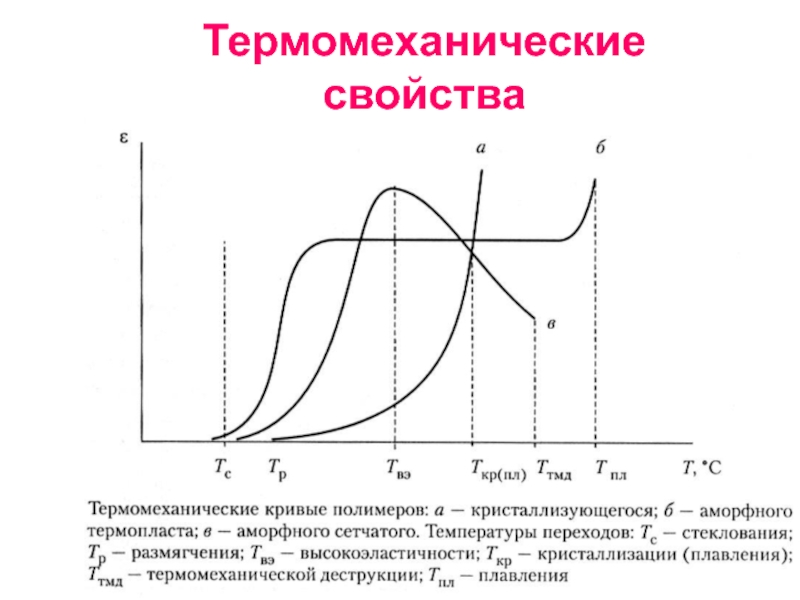
- 65. Термомеханические свойства
- 66. Дифференциальная сканирующая калориметрия Exo↓ Тс –
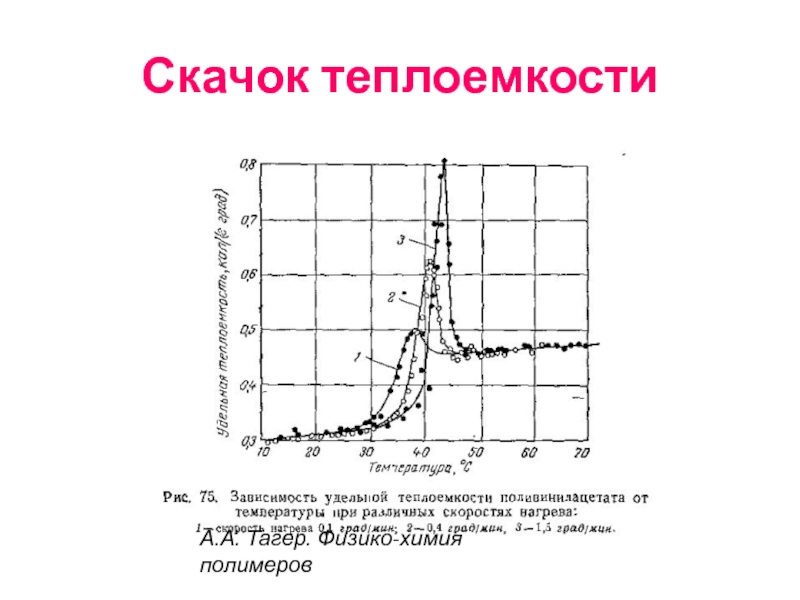
- 67. Скачок теплоемкости А.А. Тагер. Физико-химия полимеров
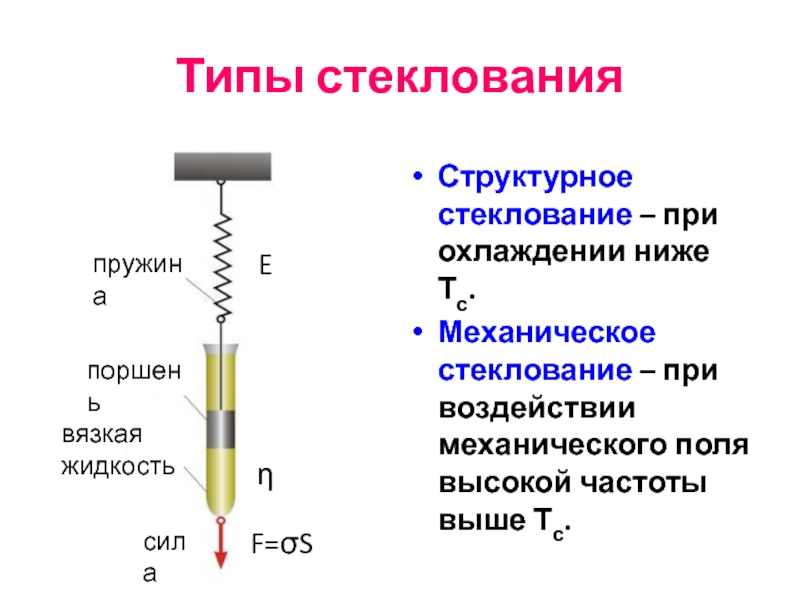
- 68. Типы стеклования Структурное стеклование – при охлаждении
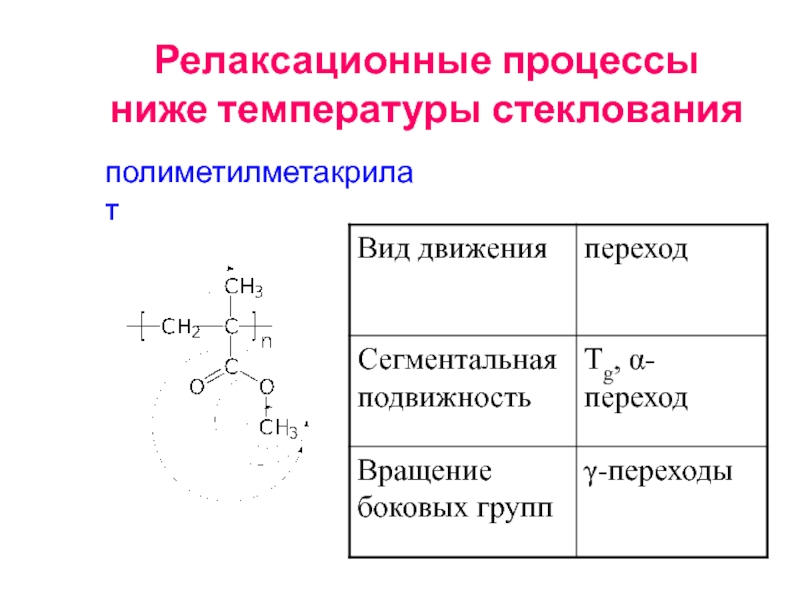
- 69. Релаксационные процессы ниже температуры стеклования полиметилметакрилат
- 70. Итак: «Дырки» в стеклообразном полимере – физические
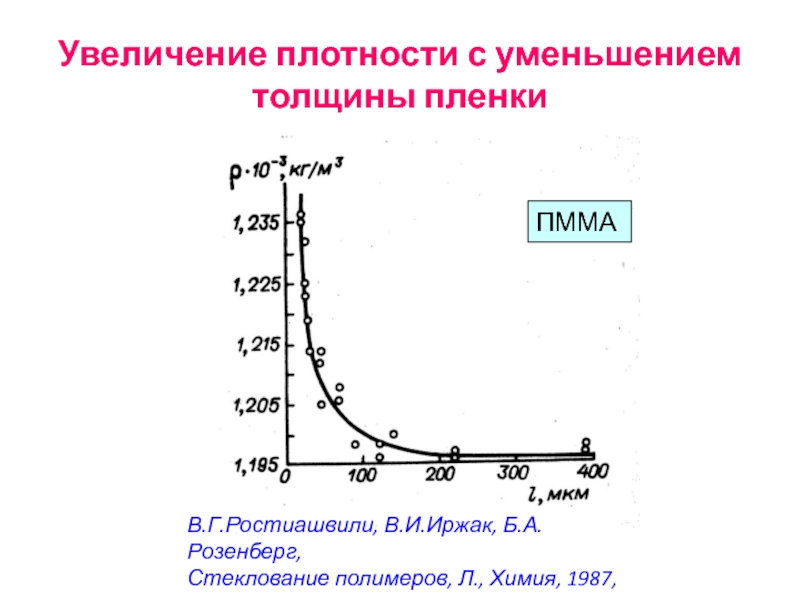
- 71. Увеличение плотности с уменьшением толщины пленки В.Г.Ростиашвили,
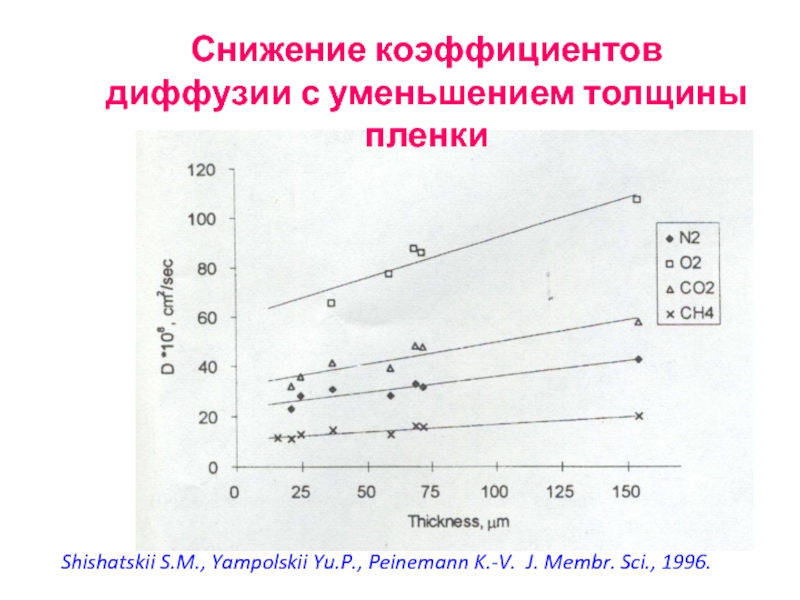
- 72. Снижение коэффициентов диффузии с уменьшением толщины пленки
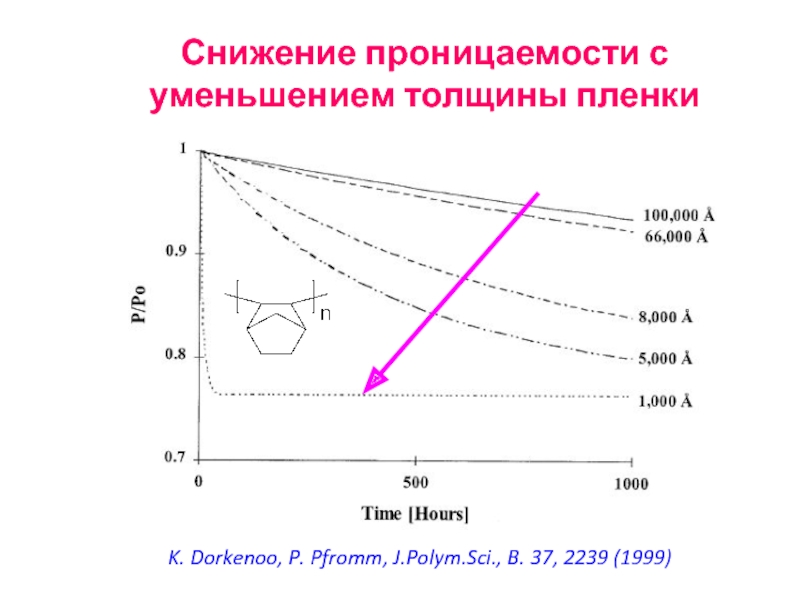
- 73. Снижение проницаемости с уменьшением толщины пленки K. Dorkenoo, P. Pfromm, J.Polym.Sci., B. 37, 2239 (1999)
- 74. M.McCaig, D.Paul, Polymer, 41(2), 629 (2000)
- 75. Термомеханическая кривая аморфного полимера Tg Tm
- 76. Свободный объем и реология полимеров
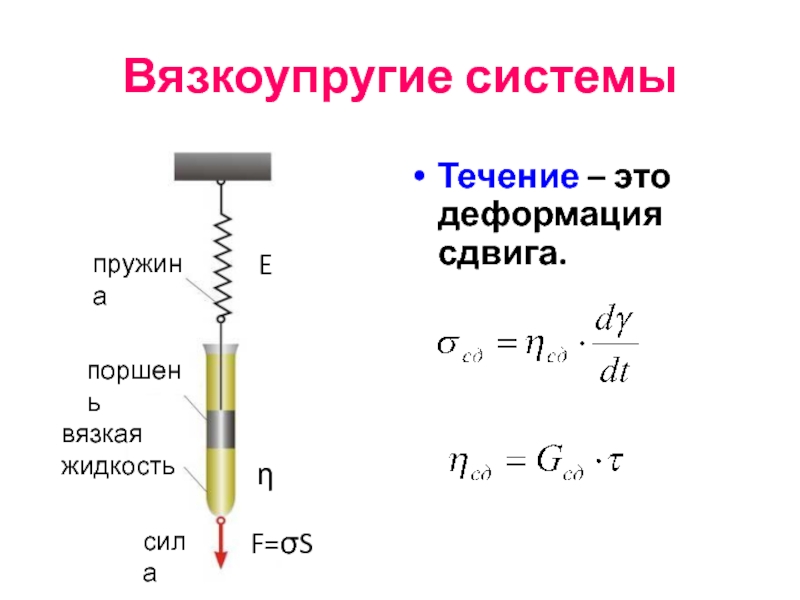
- 77. Вязкоупругие системы Течение – это деформация сдвига.
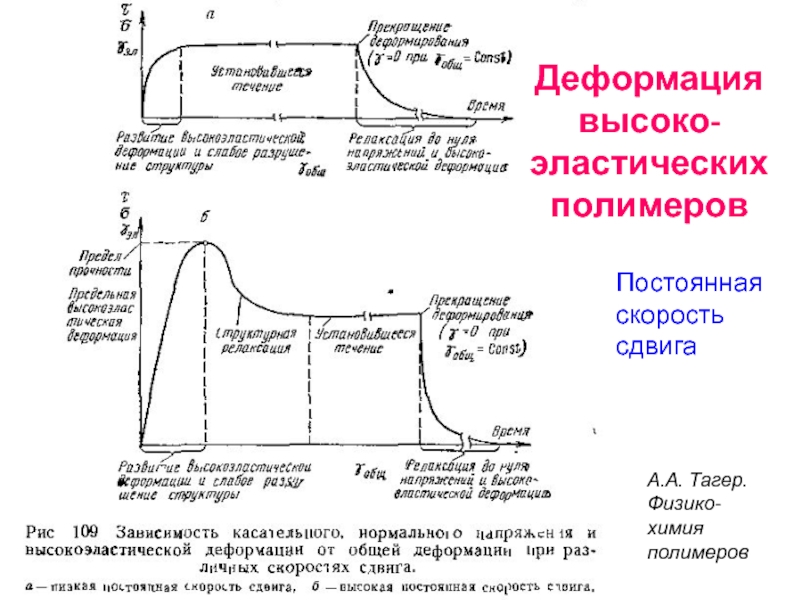
- 78. А.А. Тагер. Физико-химия полимеров Деформация высоко-эластических полимеров Постоянная скорость сдвига
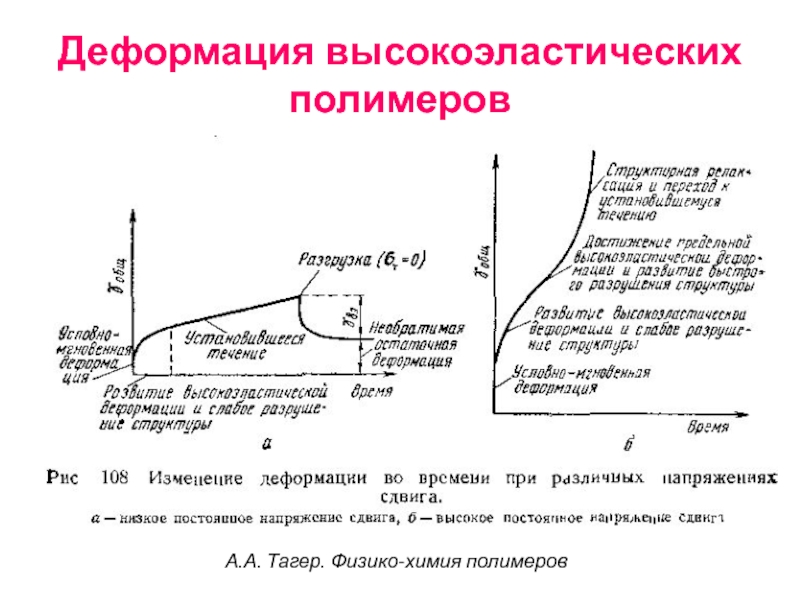
- 79. Деформация высокоэластических полимеров А.А. Тагер. Физико-химия полимеров
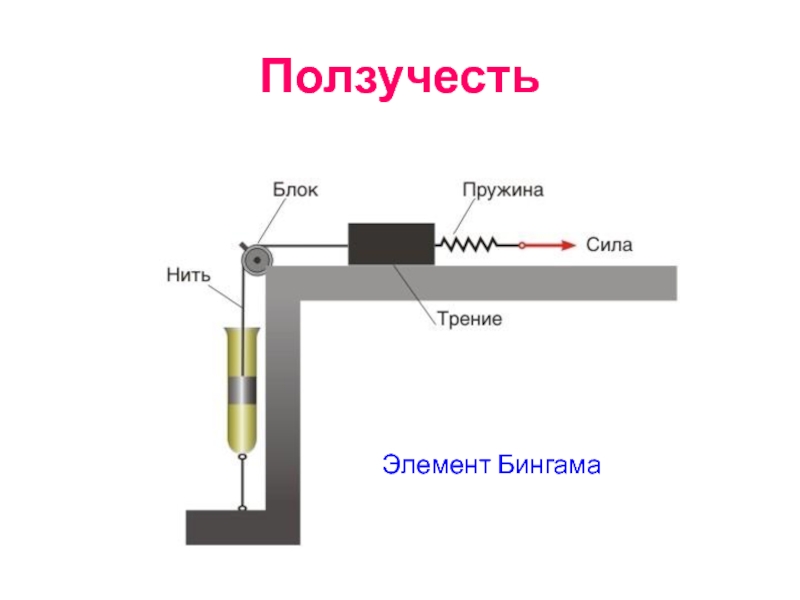
- 80. Ползучесть Элемент Бингама
- 81. Высокоэластичность вязкотекучего состояния При определенных значениях напряжения сдвига вязкая жидкость проявляет высокоэластические свойства
- 82. Высокоэластичность вязкотекучего состояния Эффект Вейсенберга При больших
- 83. Циклические нагрузки Вязкий элемент Упругий элемент
- 84. Тангенс угла механических потерь E’ E” Eкомпл
- 85. Итак: Аморфные полимеры – это жидкости с
- 86. Релаксационные состояния аморфных полимеров Стеклообразное (механически-твердое, но
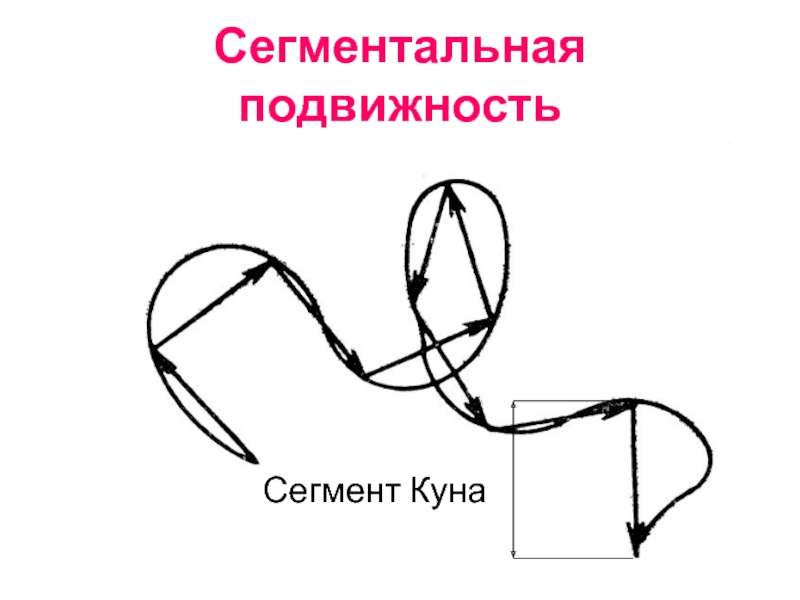
- 87. Сегментальная подвижность
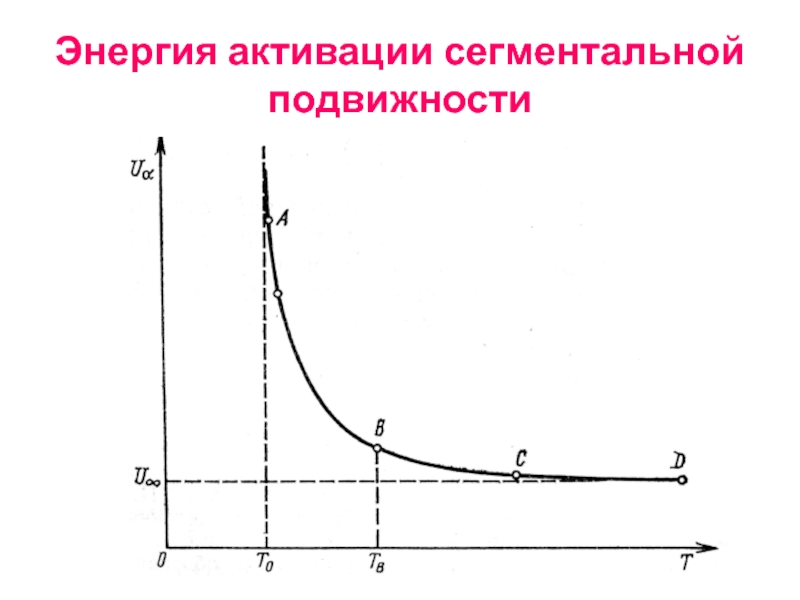
- 88. Энергия активации сегментальной подвижности
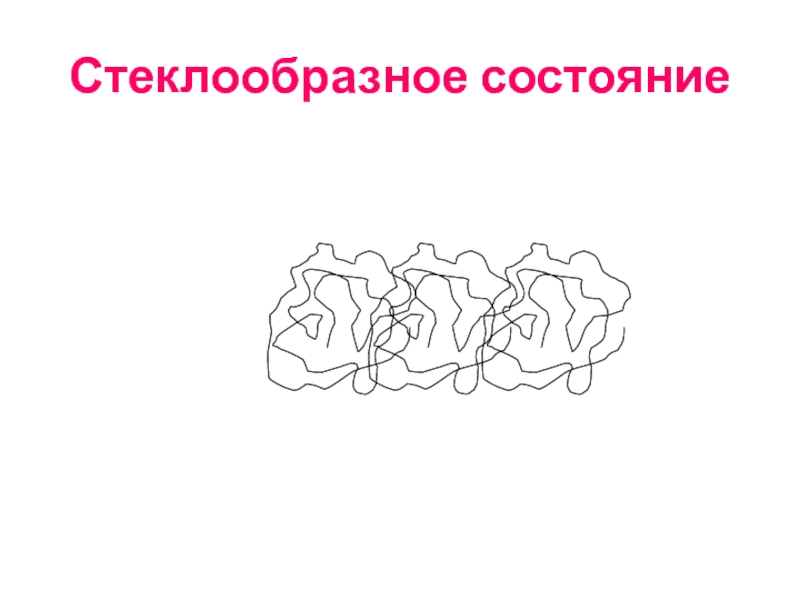
- 89. Стеклообразное состояние
- 90. Стеклообразное состояние
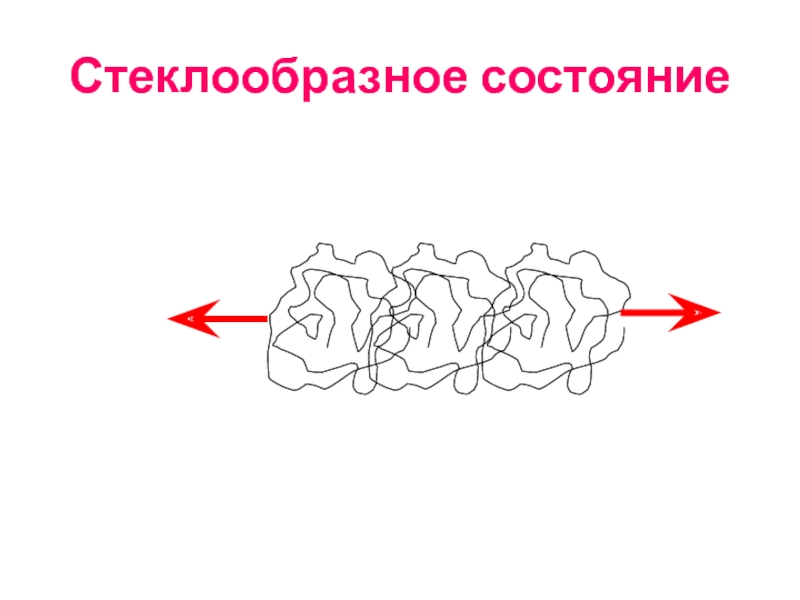
- 91. Стеклообразное состояние
- 92. Фазовое состояние полимеров Кристаллическое Жидкокристаллическое Аморфное Изотропный расплав (раствор)
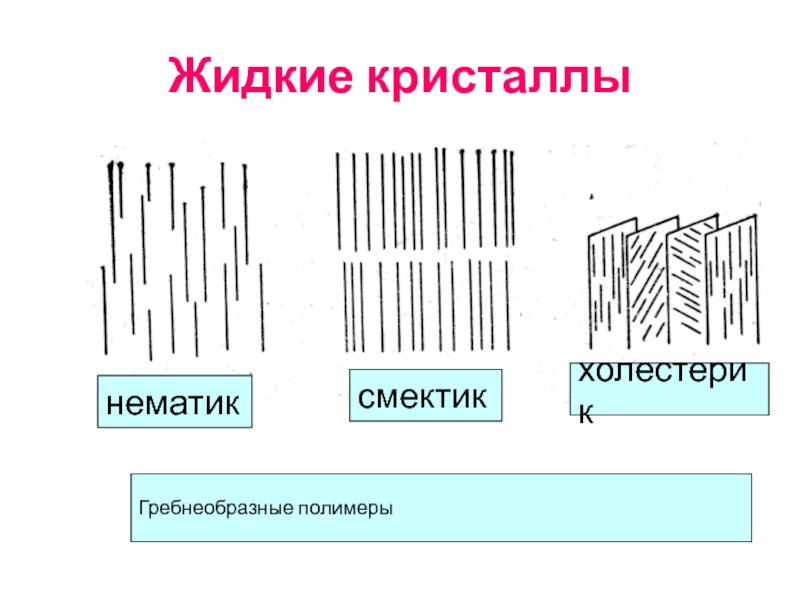
- 93. Жидкие кристаллы нематик смектик холестерик Гребнеобразные полимеры
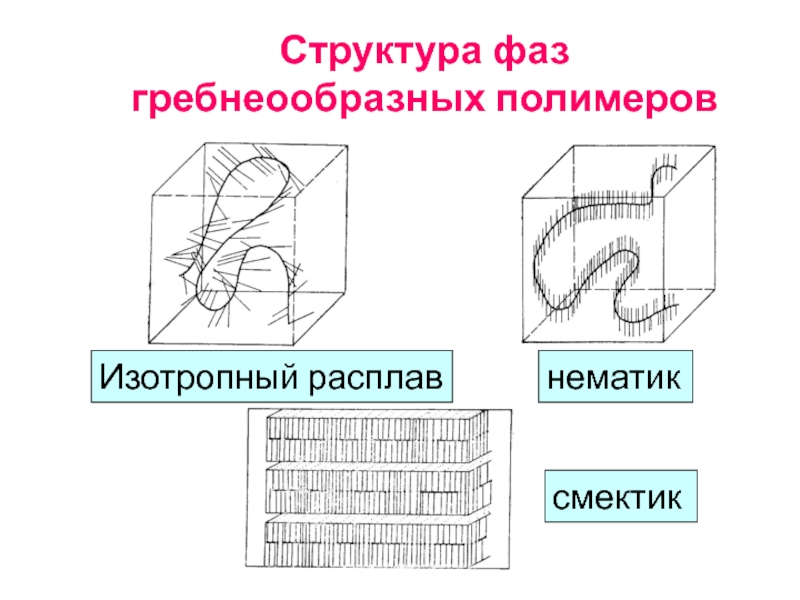
- 94. Структура фаз гребнеообразных полимеров Изотропный расплав нематик смектик
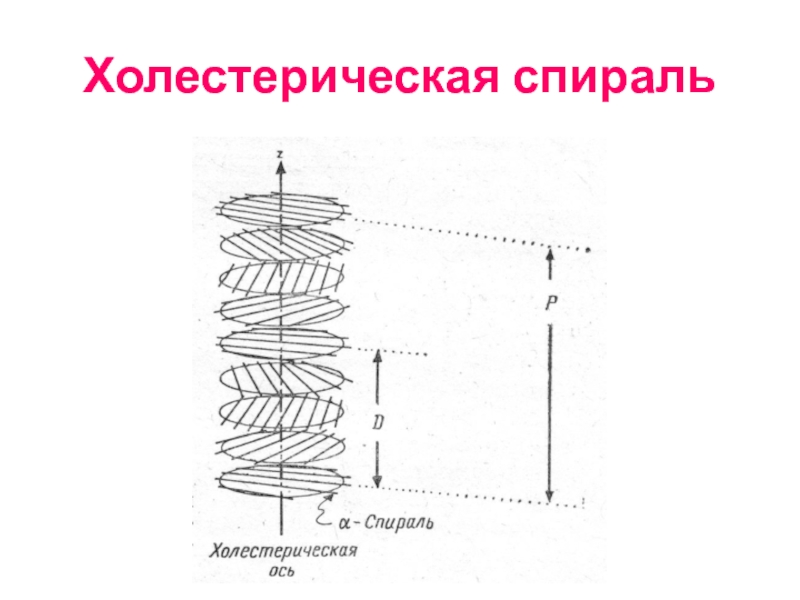
- 95. Холестерическая спираль
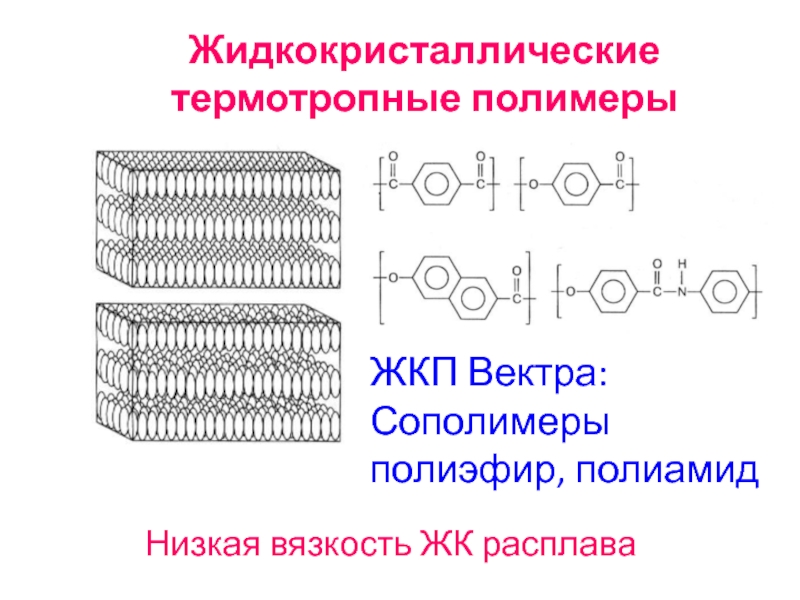
- 96. Жидкокристаллические термотропные полимеры ЖКП Вектра: Сополимеры полиэфир, полиамид Низкая вязкость ЖК расплава
Слайд 1Фазовое состояние полимеров
Кристаллическое
Жидкокристаллическое
Аморфное
Изотропный расплав (раствор)
Слайд 2Модели
аморфного
состояния
а - пачки
б - клубки
в - меандры
г - колл. клубки
д -
е - сл. фибриллы
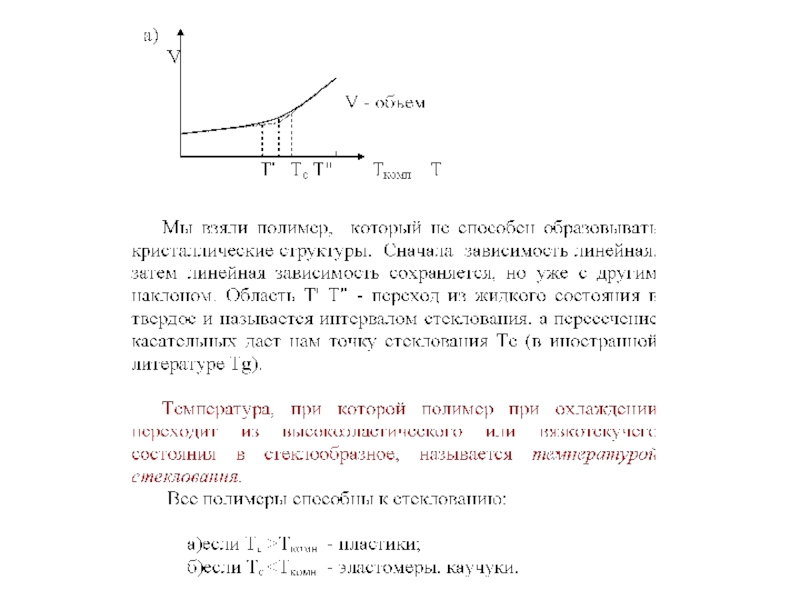
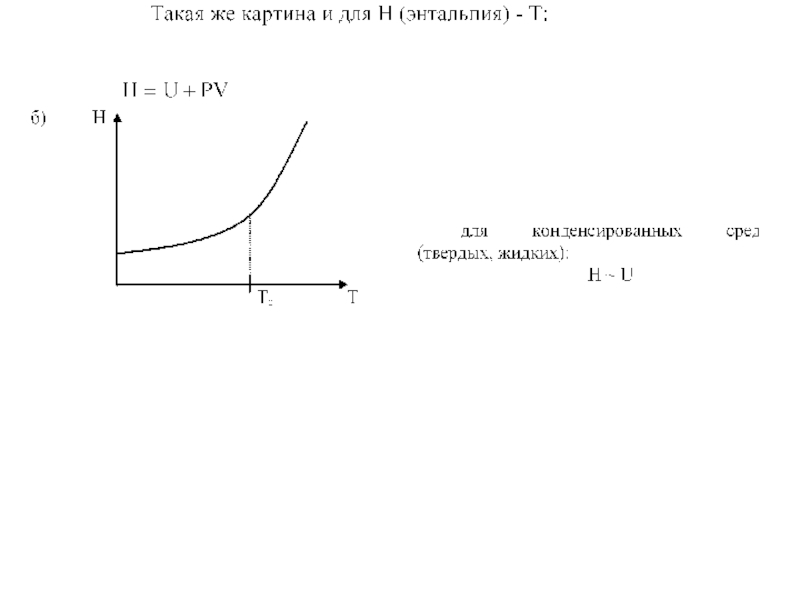
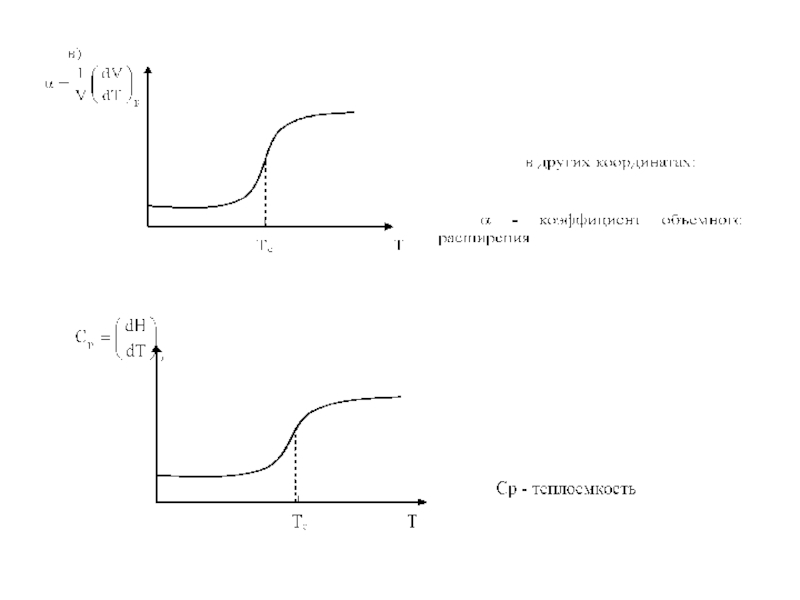
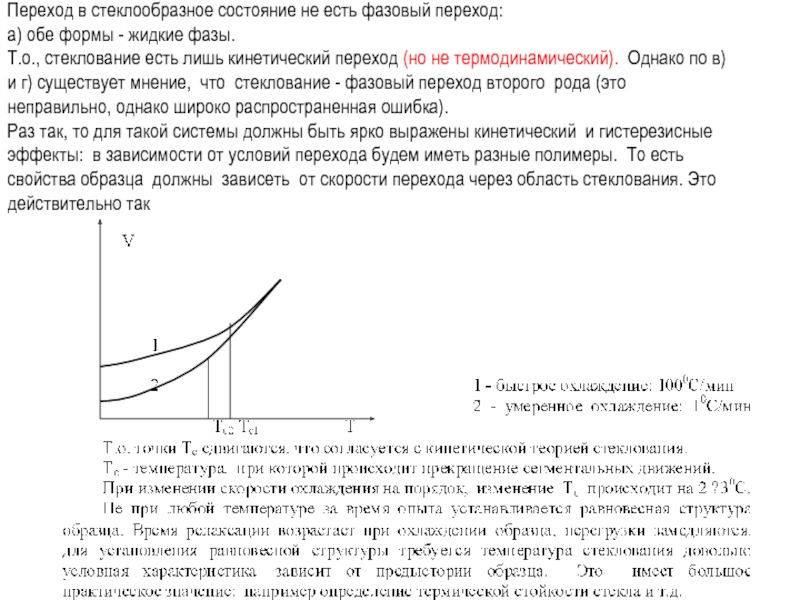
Слайд 7Переход в стеклообразное состояние не есть фазовый переход:
а) обе формы -
Т.о., стеклование есть лишь кинетический переход (но не термодинамический). Однако по в) и г) существует мнение, что стеклование - фазовый переход второго рода (это неправильно, однако широко распространенная ошибка).
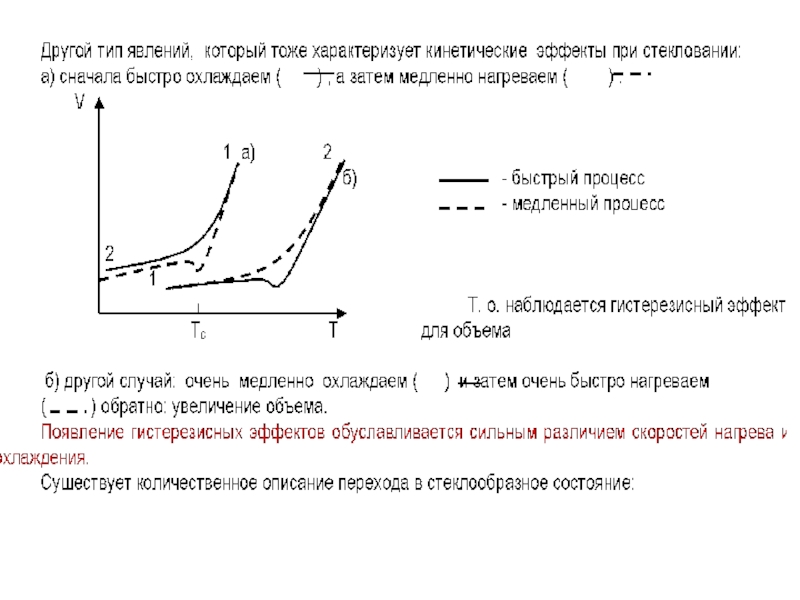
Раз так, то для такой системы должны быть ярко выражены кинетический и гистерезисные эффекты: в зависимости от условий перехода будем иметь разные полимеры. То есть свойства образца должны зависеть от скорости перехода через область стеклования. Это действительно так
Слайд 10Стеклование – фазовый переход?
Удовлетворяет критерию Эренфеста: скачок теплоемкости, следовательно, фазовый переход
Макрогалерея (университет Южного Миссисипи), русский перевод ИНЭОС + Физический факультет http://pslc.ws/russian/index.htm
Но: для аморфной фазы и стеклование, и переход в вязкотекучее состояние – это релаксационные переходы!
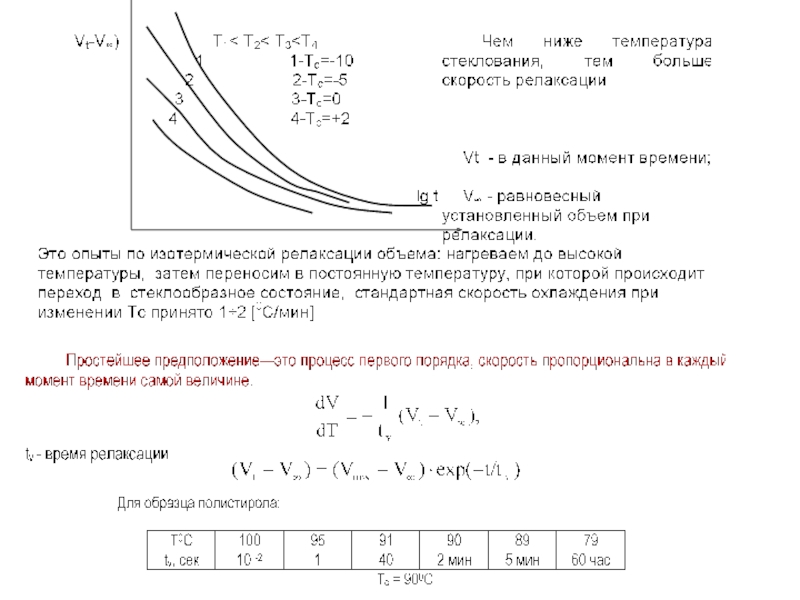
Слайд 11Делались неоднократные попытки создать физически простую модель процесса стеклования, которая бы
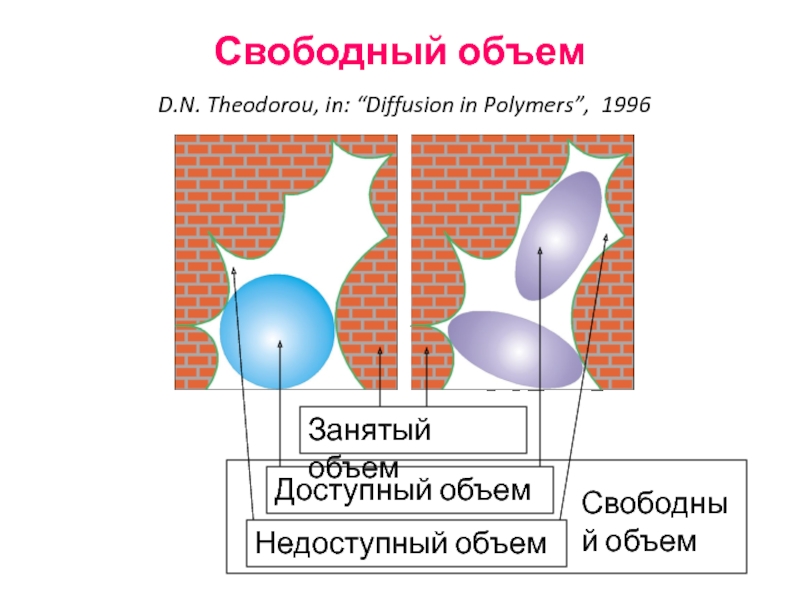
Понятие о свободном объеме:
Это разность между реальным объемом при данной То и занятым объемом (при плотно упакованном слое - без дефектов, с шахматным использованием пустот).
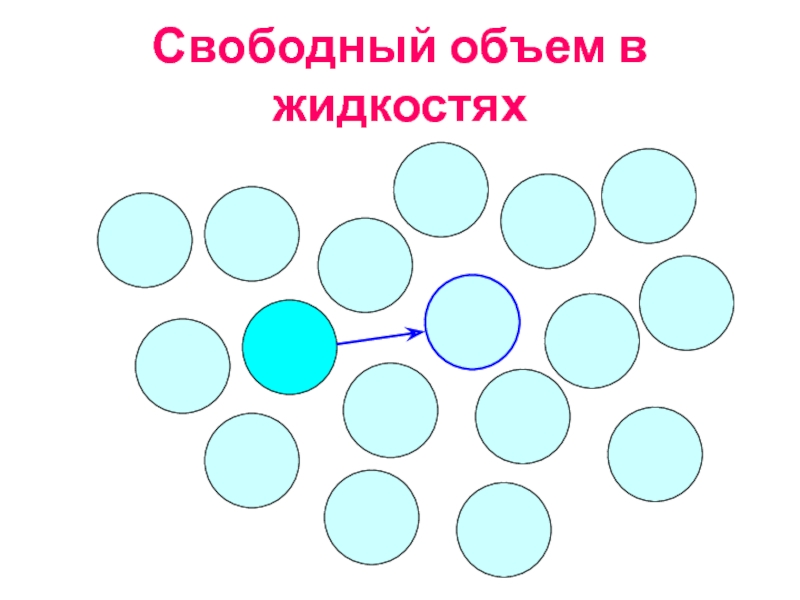
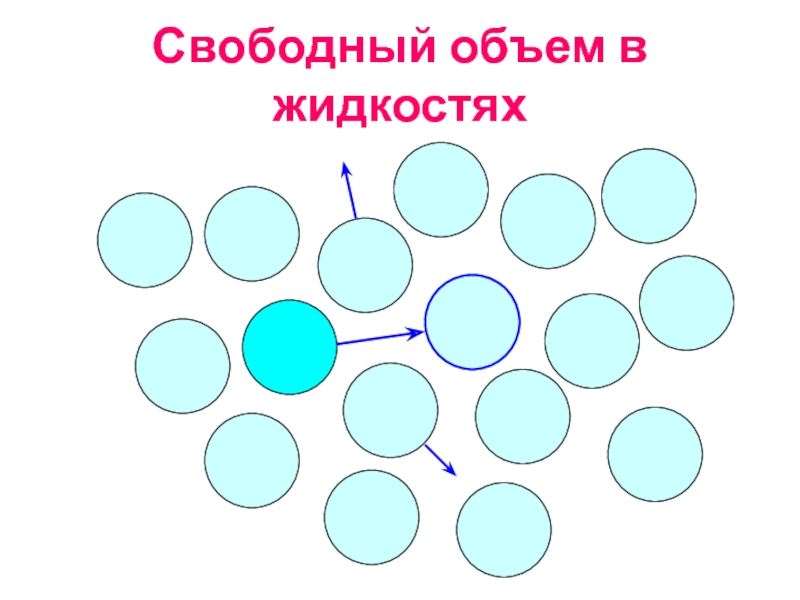
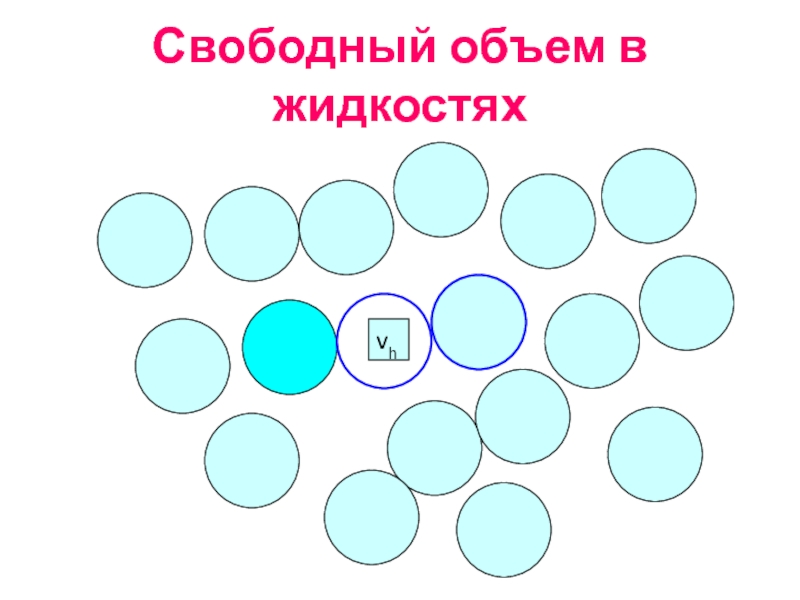
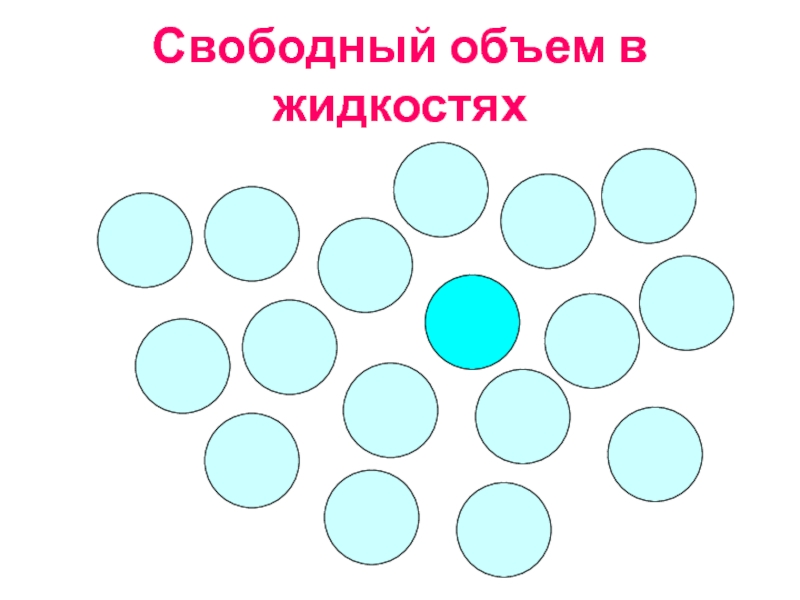
Слайд 17Свободный объем в жидкостях
Флуктуационный свободный объем определяется как
суммарный объем дырок
vf=vh·exp{(Eh+p·vh)/RT}
vh
Eh - энергия образования дырки
Френкель Я.И., Кинетическая теория жидкостей, 1959
Слайд 18Подвижность молекул жидкости
Движение частицы осуществляется, когда по соседству с ней появляется
η=a·exp(γ·vh/vf)
Коэн – Тарнбалл – Дулитл, 1959
С учетом энергетического барьера скачка молекулы:
lnη=А+E0/RT+γ·vh/vf
Слайд 26Геометрическое определение свободного объема
Vf=Vsp-Voc (Vsp=1/ρ);
f=Vf/Vsp (f=FFV=1-Voc/Vsp)
Пустой объем
Vempty=Vsp-Vw;
K=Vw/Vsp;
fempty=1-K
Слайд 29Геометрическое определение свободного объема
Vf=Vsp-Voc; f=Vf/Vsp
Свободный объем (при диффузии)
Voc=Vw+Vdead;
Vdead=Vempty (плотноупакованной
Voc=Vw/K;
Vf=Vsp-VW/K; f=1-Vw/(Vsp·K)
Vf=Vsp-1,3·VW (Бонди)
Слайд 30Теория
свободного объема
M.Cohen, T.Turnbull, 1959
D=A·exp(-B·vh/vf)
А, B, T=const
vf – свободный
vh – минимальный объем «дырки»,
достаточный для перемещения
диффундирующей молекулы
Слайд 31Теория
свободного объема
M.Cohen, T.Turnbull, 1959
D=A·exp(-B/vf)
А, B, T=const
vf=vsp-voc
vf – свободный
=1/ρ
Занятый объем
Расчетная величина
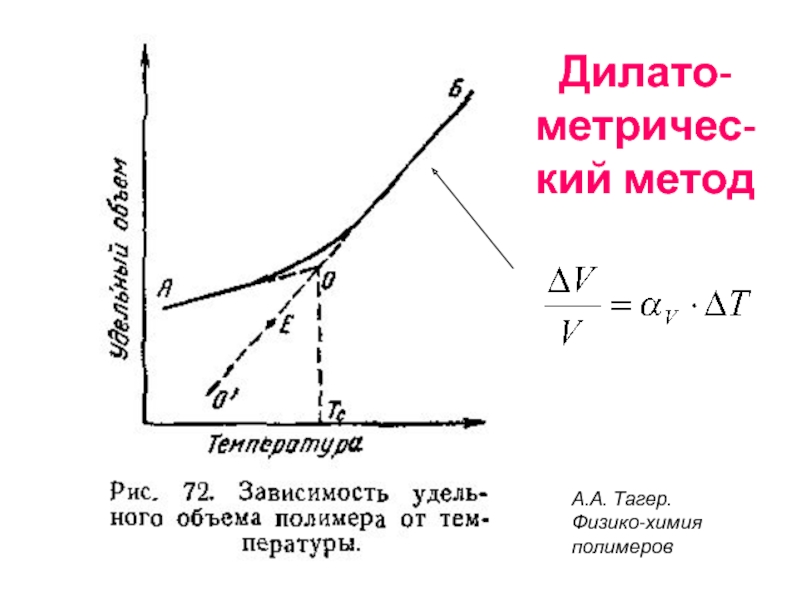
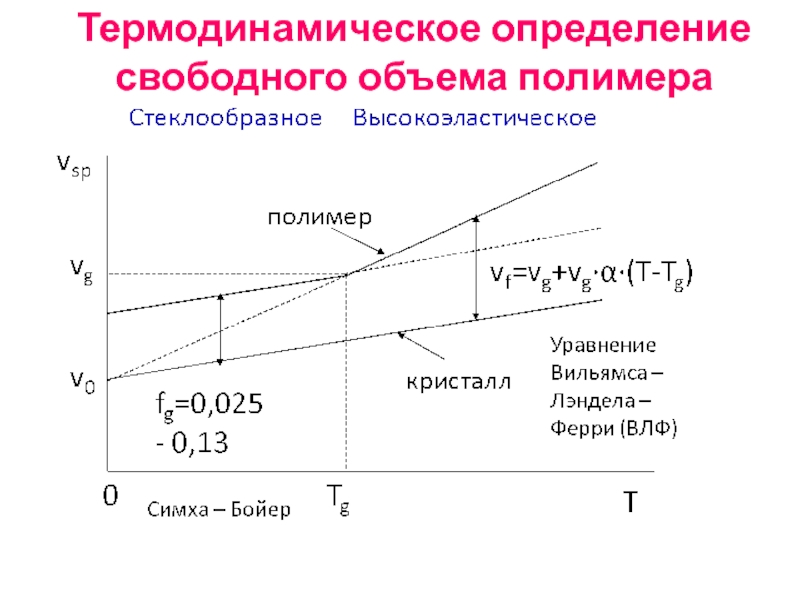
Слайд 32Термодинамическое определение свободного объема полимера
Стеклообразное
Высокоэластическое
T
Tg
0
vsp
vg
v0
кристалл
полимер
vf=vg+vgα(T-Tg)
fg=0,025 - 0,13
Симха
Уравнение Вильямса – Лэндела – Ферри (ВЛФ)
Слайд 33Тепловое расширение выше Тс определяется изменением свободного объема: он более чувствителен
α = (5·10-4 ÷1·10-3) – коэффициент объемного расширения для свободного объема выше Тс очень большой.
При Тс стеклообразных состояниях в первом приближении замораживается один и тот же объем:
где fc - объемная доля свободного пространства.
Таким образом, при охлаждении жидкой системы, когда fc =2.5%, система переходит в стеклообразное состояние (при fc >2.5% возможно перемещение сегмента под действием теплового движения).
Слайд 34Эмпирическое соотношение Дулиттла:
, где
-- вязкость, А и В—константы
тогда:
но происходит изменение доли свободного пространства зависимости от температуры:
,
fc – доля свободного объема при температуре стеклования
Тогда соответственно:
Для температуры стеклования (ниже ее не работает):
отсюда
Из этого эксперимента можно получить:
αf = 4.8·10-4 [К -1], - коэффициент сдвига или перемещения по шкале температур
В первом приближении эти константы характерны для всех стеклообразных систем. При Тс вязкость для этих систем считается 1013 Пз (как только достигает такого значения, то значит тело перешло в стеклообразное состояние
Получаем уравнение, названное уравнением Вильямса-Лендела-Ферри:
Формула применима при температуре: Тc < T < Tc + 100˚С
Слайд 37Наибольшая ньютоновская вязкость
Вязкость, при которой жидкость ЕЩЕ ведет себя как ньютоновская
Уравнение
Уравнение Коэна - Тарнбалла
Слайд 38Зависимость наибольшей ньютоновской вязкости от молекулярной массы
А.А. Тагер. Физико-химия полимеров
Критическая молекулярная
Слайд 40Для газов:
D=AD·exp(-BD/vf)
P=D·S
D – меняется на порядки
S – мало зависит от свойств
P=AP·exp(-BP/vf)
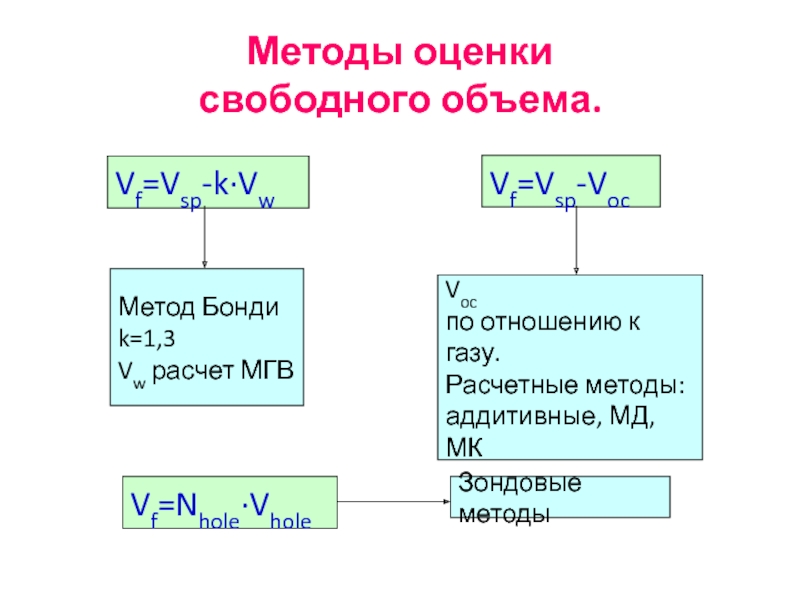
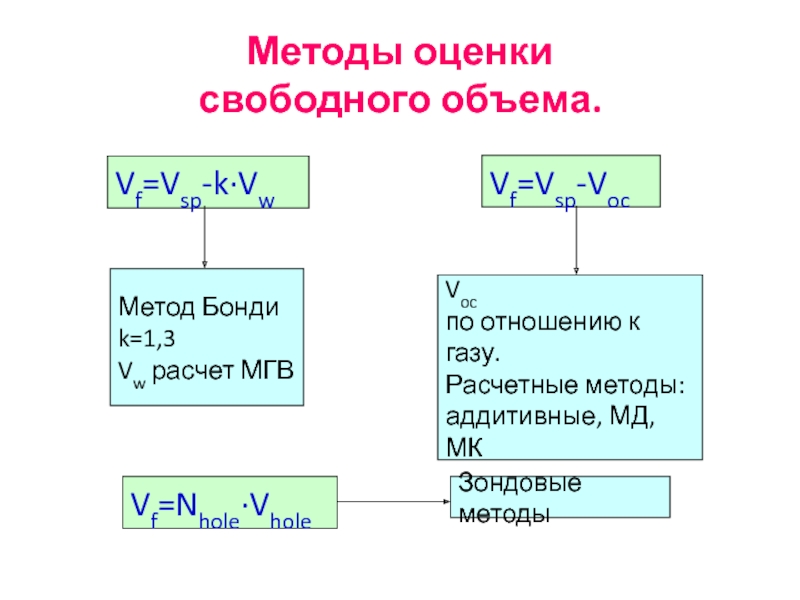
Слайд 42Методы оценки
свободного объема.
Vf=Vsp-k·Vw
Метод Бонди
k=1,3
Vw расчет МГВ
Vf=Vsp-Voc
Vf=Nhole·Vhole
Voc
по отношению к газу.
Расчетные
аддитивные, МД, МК
Зондовые методы
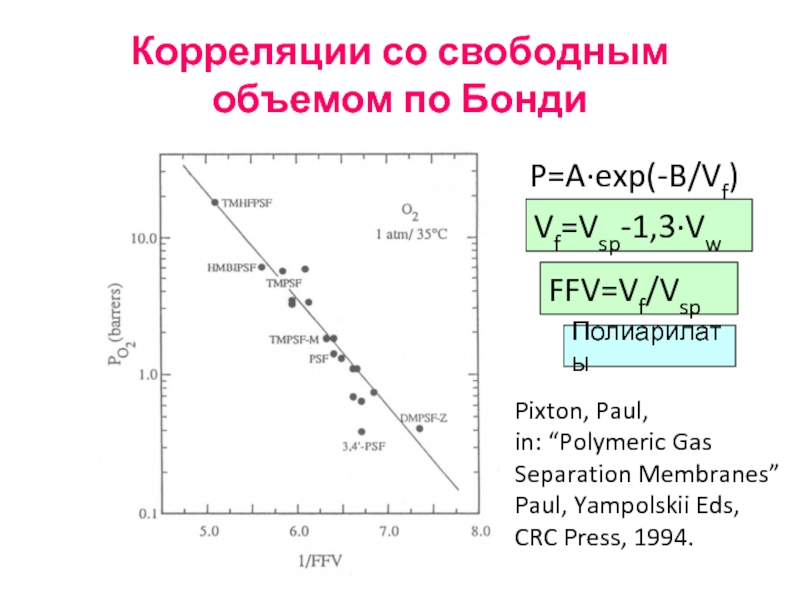
Слайд 43Корреляции со свободным объемом по Бонди
P=A·exp(-B/Vf)
Vf=Vsp-1,3·Vw
Полиарилаты
Pixton, Paul,
in: “Polymeric Gas
Separation
Paul, Yampolskii Eds,
CRC Press, 1994.
FFV=Vf/Vsp
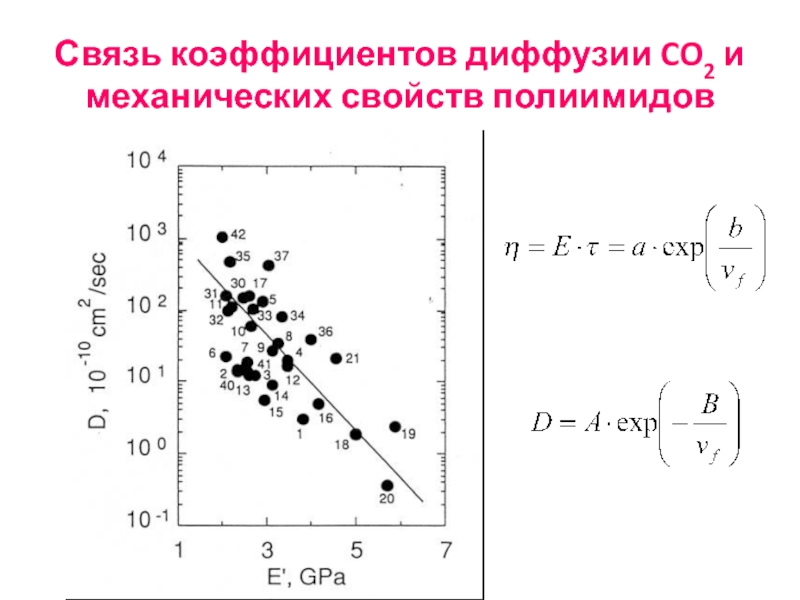
Слайд 44Корреляции со свободным объемом по Бонди
D=A·exp(-B/Vf)
Vf=Vsp-1,3·Vw
Полиимиды
Hirayama, et. al.,
J. Membr.
Слайд 47Методы оценки
свободного объема.
Vf=Vsp-k·Vw
Метод Бонди
k=1,3
Vw расчет МГВ
Vf=Vsp-Voc
Vf=Nhole·Vhole
Voc
по отношению к газу.
Расчетные
аддитивные, МД, МК
Зондовые методы
Слайд 48
Свободный объем
D.N. Theodorou, in: “Diffusion in Polymers”, 1996
Занятый объем
Доступный
Недоступный объем
Свободный объем
Слайд 49Методы оценки
свободного объема.
Vf=Vsp-k·Vw
Метод Бонди
k=1,3
Vw расчет МГВ
Vf=Vsp-Voc
Vf=Nhole·Vhole
Voc
по отношению к газу.
Расчетные
аддитивные, МД, МК
Зондовые методы
Слайд 50Зондовые методы
1. Методы с переменным размером зонда:
Сорбция газов и паров (CH’)
Обращенная
Спиновые зонды
Фотохромные зонды
Электрохромные зонды
Конформационные зонды (ИК)
Проницаемость и диффузия газов
2. Методы с постоянным размером зонда
Аннигиляция позитронов
129Xe-ЯМР
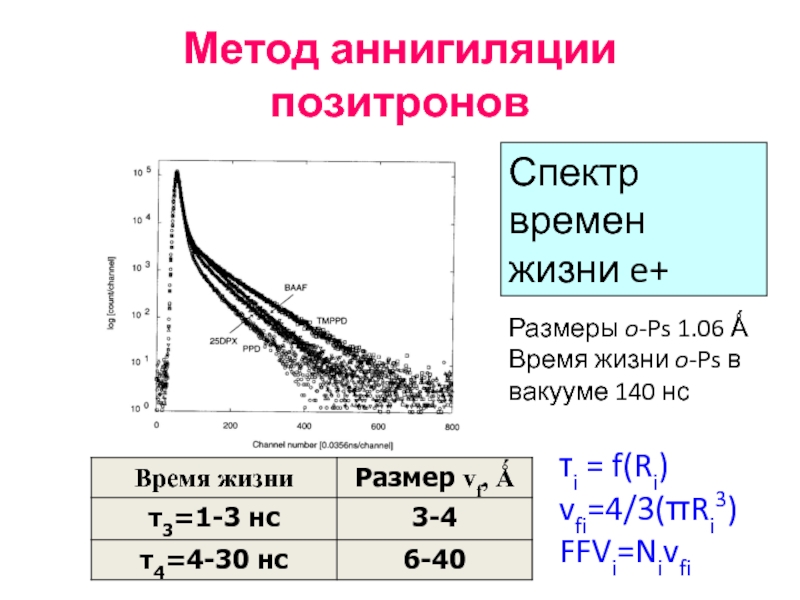
Слайд 51Метод аннигиляции позитронов
Спектр времен жизни e+
Размеры o-Ps 1.06 Ǻ
Время жизни o-Ps
τi = f(Ri)
vfi=4/3(πRi3)
FFVi=Nivfi
Слайд 54Подвижность «дырок»
Изменение характеристик пленки с изменением ее толщины
Следствие релаксационных процессов в
Масштабный эффект
Слайд 59Пластификация
Термодинамическая совместимость с полимером (истинный раствор)
Следовательно, «разбавление» раствора, увеличение подвижности цепей
Отсутствие «сильных» взаимодействий с функциональными группами полимера
Следовательно, ВСЕГДА снижение Тс и увеличение пластичности материала
Для пластификаторов пластмасс важно: нелетучесть (в условиях эксплуатации), отсутствие «выпотевания», нетоксичность, химическая стойкость, температура разложения ниже температуры переработки полимера
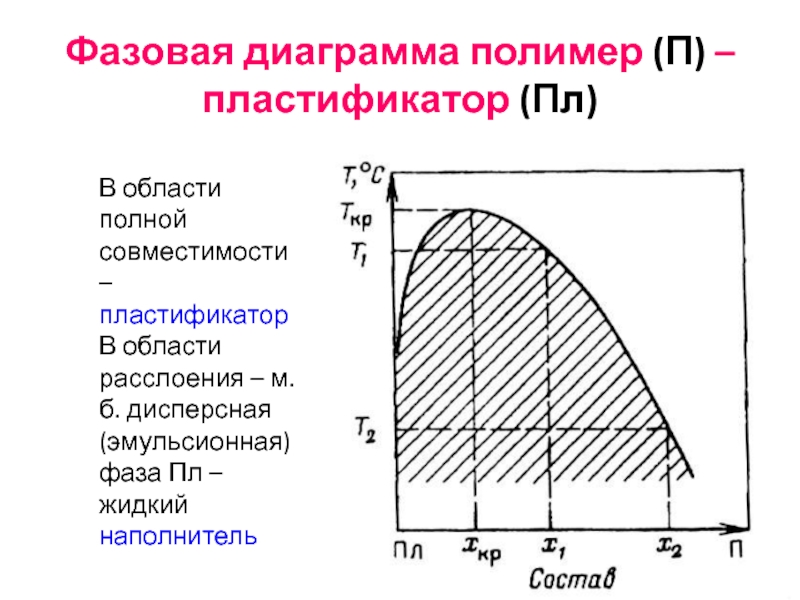
Слайд 62Фазовая диаграмма полимер (П) – пластификатор (Пл)
В области полной совместимости –
В области расслоения – м.б. дисперсная (эмульсионная) фаза Пл – жидкий наполнитель
Слайд 63Антипластификация
Термодинамическая совместимость с полимером (истинный раствор)
Следовательно, «разбавление» раствора, увеличение подвижности цепей
Наличие «сильных» взаимодействий с функциональными группами полимера
Следовательно, увеличение Тс и увеличение жесткости материала
Поэтому, антипластификация может приводить как к снижению, так и к увеличению Тс, а, следовательно, к возможности управления свойствами пластмасс.
Вопрос изучен мало
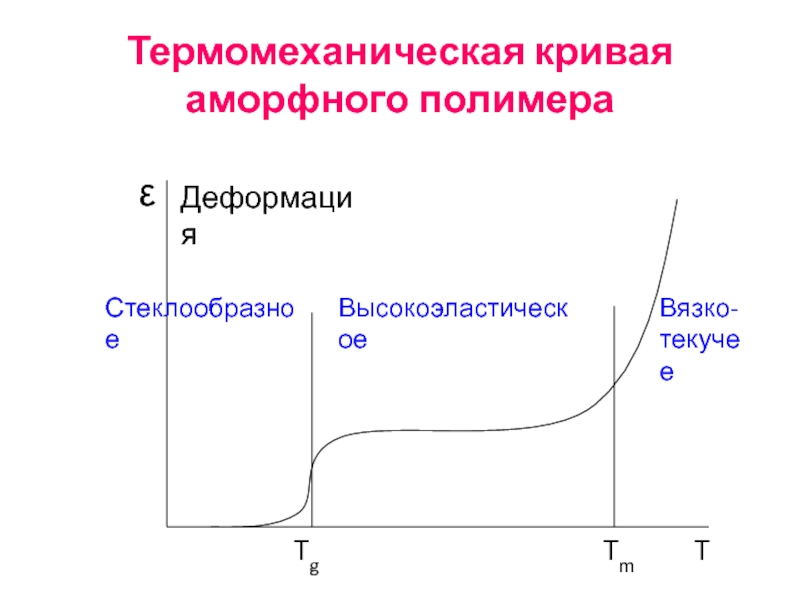
Слайд 64Термомеханическая кривая аморфного полимера
Tg
Tm
T
ε
Стеклообразное
Высокоэластическое
Вязко-
текучее
Деформация
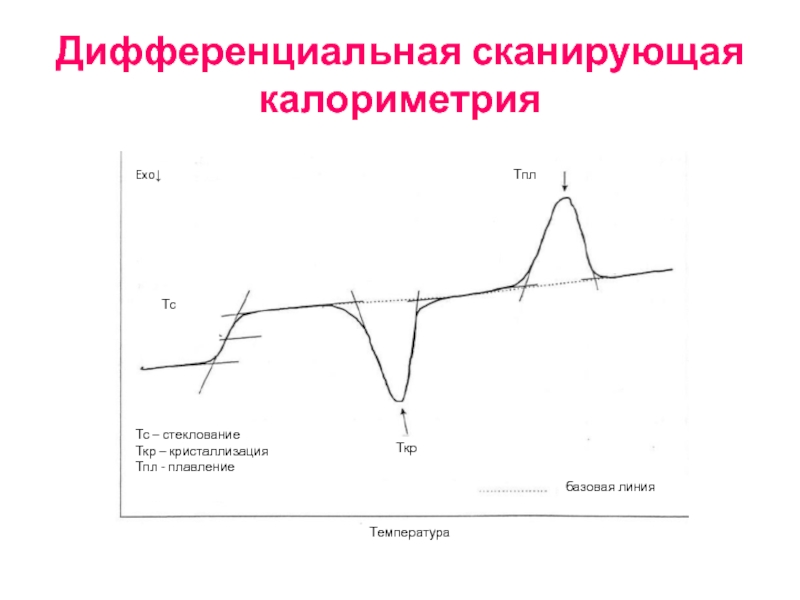
Слайд 66Дифференциальная сканирующая калориметрия
Exo↓
Тс – стеклование
Ткр – кристаллизация
Тпл - плавление
Температура
базовая линия
Тс
Ткр
Тпл
Слайд 68Типы стеклования
Структурное стеклование – при охлаждении ниже Тс.
Механическое стеклование – при
Слайд 70Итак:
«Дырки» в стеклообразном полимере – физические объекты, характерный размер и подвижность
Средний размер «дырок» в стеклообразном полимере определяет его газопроницаемость
Средняя концентрация «дырок» в стеклообразном полимере – величина постоянная
Слайд 71Увеличение плотности с уменьшением толщины пленки
В.Г.Ростиашвили, В.И.Иржак, Б.А.Розенберг,
Стеклование полимеров, Л.,
ПММА
Слайд 72Снижение коэффициентов диффузии с уменьшением толщины пленки
Shishatskii S.M., Yampolskii Yu.P., Peinemann
Слайд 73Снижение проницаемости с уменьшением толщины пленки
K. Dorkenoo, P. Pfromm, J.Polym.Sci., B.
Слайд 74M.McCaig, D.Paul, Polymer, 41(2), 629 (2000)
В.Г.Ростиашвили, В.И.Иржак, Б.А.Розенберг,
Стеклование полимеров,
Диффузия «дырок» (элементов свободного объема) к поверхности образца (пленка, мембрана)
Причины масштабного эффекта
По скорости старения и профилю плотности определяется коэффициент диффузии «дырок» в стеклообразных полимерах
D = 10-14 – 10-16 см2/с
Слайд 75Термомеханическая кривая аморфного полимера
Tg
Tm
T
ε
Стеклообразное
Высокоэластическое
Вязко-
текучее
Деформация
Слайд 78А.А. Тагер. Физико-химия полимеров
Деформация высоко-эластических полимеров
Постоянная скорость сдвига
Слайд 81Высокоэластичность вязкотекучего состояния
При определенных значениях напряжения сдвига вязкая жидкость проявляет высокоэластические
Слайд 82Высокоэластичность вязкотекучего состояния
Эффект Вейсенберга
При больших скоростях деформирования вязкоупругие жидкости способны к
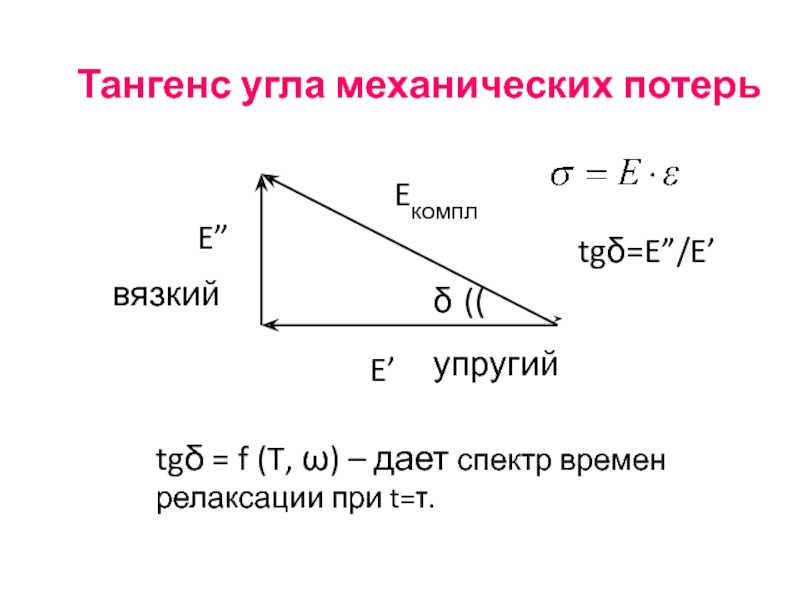
Слайд 84Тангенс угла механических потерь
E’
E”
Eкомпл
упругий
вязкий
((
tgδ=E”/E’
δ
tgδ = f (T, ω) – дает спектр
Слайд 85Итак:
Аморфные полимеры – это жидкости с большой вязкостью и большим временем
Понимание физических свойств полимеров немыслимо без изучения их деформационных и реологических характеристик
Слайд 86Релаксационные состояния аморфных полимеров
Стеклообразное (механически-твердое, но структурно-жидкое)
Высокоэластическое (структурно-жидкое с огромными обратимыми
Вязкотекучее (механически и структурно-жидкое с необратимыми деформациями)