- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Физическое материаловедение презентация
Содержание
- 1. Физическое материаловедение
- 2. ПРОБЛЕМЫ И ДОСТИЖЕНИЯ МАТЕРИАЛОВЕДЕНИЯ Существует тесная зависимость
- 3. продолжение «эффект памяти» – восстановление первоначальной формы
- 4. Атом Атом – наименьшая частица химического элемента,
- 5. продолжение Кванты электромагнитного поля –
- 6. продолжение Согласному одному из законов квантовой механики
- 7. ХИМИЧЕСКАЯ СВЯЗЬ Под химической с вязью понимают
- 8. продолжение Согласно классической теории валентности, каждой связи
- 9. продолжение Так, в образовании ковалентной связи в
- 10. СХЕМА ОБРАЗОВАНИЯ ИОННОЙ СВЯЗИ В МОЛЕКУЛЕ ХЛОРИСТОГО НАТРИЯ
- 11. продолжение Признаком соединений с ионной связью
- 12. МОЛЕКУЛА Молекула – наименьшая частица вещества, обладающая
- 13. ГЕОМЕТРИЧЕСКИЕ ФОРМЫ МОЛЕКУЛ С КООРДИНАЦИОННЫМИ СВЯЗЯМИ (СОЕДИНЕНИЯ
- 14. продолжение Изомерия - явление,
- 15. продолжение В 1940-х годов были созданы методы
- 16. продолжение Молекулы электронейтральны, однако если «центры тяжести»
- 17. ФАЗОВОЕ СОСТОЯНИЕ ВЕЩЕСТВА Физические свойства веществ
- 18. продолжение В веществе выделяется или
- 19. продолжение При фазовых переходах I рода
- 20. Агрегатные состояния Проблема структуры макротел связана с
- 21. продолжение Процесс плавления характеризуется теплотой плавления. Внутри
- 22. твердое тело .Твердое тело характеризуется стабильностью форм,
- 23. продолжение Ребра элементарных ячеек обозначают буквами «a,
- 25. продолжение Любому атому в элементарной ячейке кристал-
- 26. продолжение Твердые материалы являются, как правило, поликристаллическими,
- 27. Особое положение занимает поверхность.
- 28. Типы кристаллических решеток Исходя из вида элементов
- 29. Большая часть солей, окислов, сульфидов об-
- 30. 2. Атомные кристаллы (атомная
- 31. 3. Молекулярные кристаллы (молекулярная решетка) – эле-
- 33. Дефекты кристаллической решетки. В идеальном кристалле элементы
- 34. Если дефект образуется вблизи поверхности
- 35. Дефекты решетки возникают также
- 36. Наряду с локальными дефектами решетки существуют
- 37. В случае образования сплавов могут реализо-
- 38. Силы в кристаллической решетке Между элементами кристаллической
- 39. С увеличением межатомного расстояния
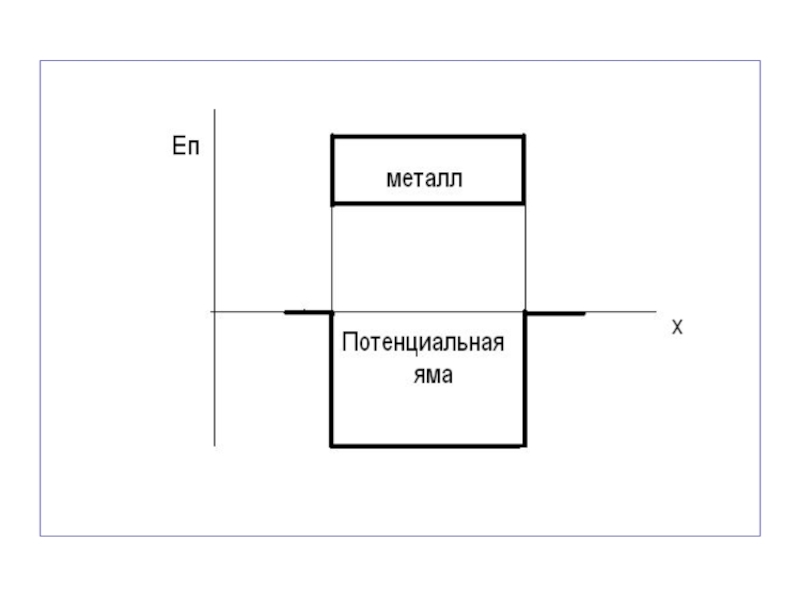
- 40. Металлы и их сплавы. В изолированных атомах
- 41. Еще чаще металлы обладают гранецентрированной кубичес-
- 42. В качестве еще одного примера следует
- 43. Решающее значение для технического применения металлов
- 44. ТЕРМОДИНАМИЧЕСКОЕ РАВНОВЕСИЕ ОБЩИЕ УСЛОВИЯ РАВНОВЕСИЯ Многие металлы
- 45. Гетерогенная смесь всегда многофазна ( смесь жидкой
- 46. Как показывает термодинамическое рассмотрение, для рав –
- 47. В случае, если заданы не «р» и
- 48. МОДЕЛИРОВАНИЕ СТРУКТУРЫ МАТЕРИАЛОВ Моделирование – метод научного
- 49. Химическую активность проявляет фильтрующий материал на основе
- 50. получивших название волновых функций и уровни
- 51. Механические свойства Механические свойства материалов характеризуют возмож-
- 52. Критическому расстоянию α’ соответствует максимальная по абсолютной
- 53. Деформирование - изменение относительного расположения частиц
- 55. Из-за дефектов в материале экспериментальная прочность
- 56. При сдвиге в материале по направлению сдвига
- 57. Для однородных изотропных тел модули упругости одинаковы
- 58. Предел прочности – напряжение, соответствующее максима –
- 59. Динамические характеристики Динамическая прочность – сопротивление материала
- 60. Усталость - процесс накоп- ления повреждений в
- 61. усталости. Усталостный процесс характеризуется зависимос- тью между
- 62. Твердость является механической характеристикой материа- лов, комплексно
- 64. Триботехнические характеристики содержат информацию об эффективности применения
- 65. Основные триботехнические характеристики твердых матери- алов -
- 66. структуры поверхностных слоев материала и протекает с
- 67. Напряжения и деформации При нагружении в металлах
- 68. С возрастанием механических нагрузок напряженно-дефор - мированное
- 69. Схема деформаций металла при сдвиге: а) –
- 70. Схема деформаций металла при сдвиге: г) проявление
- 71. В идеальном кристалле, не имеющем дефектов структуры,
- 72. Термическая обработка Термическую обработку мы разберем на
- 73. Характерный вид графика термической обработки
- 74. от исходной температуры Т(0) до заданной температуры
- 75. превращения и медленное охлаждение, приводящее сплав в
- 76. Наноматериалы Наноструктурные материалы, или наноматериалы, содер- жат
- 77. В 1969 г. советский физикохимик П.А.Рибиндер выдвинул
- 78. В 1981 г. был создан сканирующий туннельный
- 79. В настоящее время считают приоритетными направлению: Молекулярный
- 80. Классификация наноматериалов Консолидированные наноматериалы - конструкционные мате-
- 81. С(70). Их поверхность состоит из 5- и
- 82. Супрамолекулярные структуры в большей мере (лат. supra
- 83. Свойства наноматериалов Свойства наноматериалов в
- 84. Переход от крупнокристаллических к наноструктурным полу –
- 85. Границы раздела между частицами являются препятствиями на
- 86. Схема «конструирования» структуры материала методом нанотехнологии: 1.-
- 87. КОМПОЗИЦИОННЫЕ МАТЕРИАЛЫ Основные определения и классификация Композиционные
- 88. Размер фазовых включений в композите обычно
- 89. Главная функция переходного слоя состоит в том,
- 90. Синергизм (в медицине) - объединенное действие двух лекар-
- 91. б) Металлические композиты (в том числе получаемые
- 92. 2) улучшают технологичность композитов, т.е. их приспособ-
- 93. По размеру фазовых включений разработчики материалов из-
- 96. Теплоемкость. Общие сведения. Под теплоемкостью тела, С,
- 97. Где СР – молярная теплоемкость при постоянном
- 98. Электронная теплоемкость при гелиевых температурах может значительно
- 99. Анализ имеющегося в литературе большого
- 100. Уменьшение теплоемкости при понижении
- 101. Дебай в 1912 г. установил необходимость учета
- 102. Опыт показывает, что с помощью
- 103. Свободные электроны в металле Природа носителей тока
- 104. Как отмечалось выше, при образовании кристаллической ре
- 105. В отсутствие электрического поля в проводнике свободные
- 106. Закон Ома в классической электронной теории Непосредственной
- 107. По второму закону Ньютона а = F/m
- 108. В рамках классической электронной теории доказывается, что
- 109. Затруднения классической теории металлов Классическая электронная теория
- 110. ЭЛЕМЕНТЫ КВАНТОВОЙ ТЕОРИИ ТВЕРДЫХ ТЕЛ Основные положения
- 111. Квантовая теория утверждает, что энергия свободных элект-
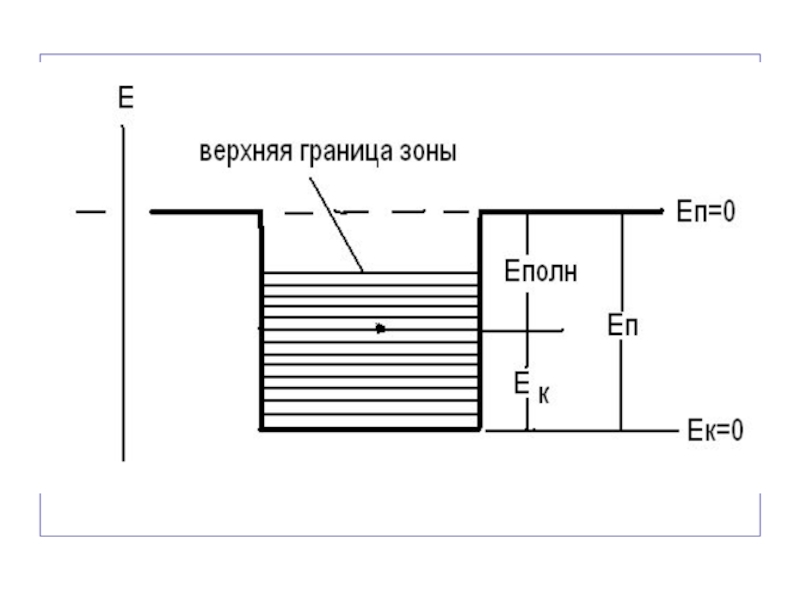
- 112. Квантование энергии свободных электронов в металле Полная
- 114. При образовании из отдельных атомов кристаллического тела
- 115. t
- 116. Заполнение разрешенных энергетических уровне происходит в соответствии
- 117. Если классические частицы должны при температуре 0
- 118. Функция распределения электронов по энергетическим состоя ниям
- 119. Теплоемкость электронов в металле и п/проводнике В
- 121. Так, в рамках модели Лаббе - Фриделя
Слайд 2ПРОБЛЕМЫ И ДОСТИЖЕНИЯ МАТЕРИАЛОВЕДЕНИЯ
Существует тесная зависимость эффективности современного машиностроения от достижений
материаловедения. Наиболее актуальные проблемы современного материаловедения и
успехи на пути их решения:
-повышение прочности материалов – важнейшая задача материаловедения во все времена.
к началу ХХI века прочность основных машиностроительных материалов возросла в 8 ..10 раз
по сравнению с началом ХХ , напряжения, при которых происходит разрушение высокопрочных
сталей, превышает 100 МПа. Перед наукой стоит задача сделать высокопрочные материалы
надежными и недорогими.
-высокопрочные материалы (твердые сплавы, карбиды, бориды, технические алмазы м пр.) в
Значительной мере характеризуют техническую мощь страны . Они не поддаются обработке
традиционными методами . Технологические трудности были преодолены только во второй
ХХ века с помощью явления «сверхпластичности».
-тенденция машиностроения к уменьшению эффективной массы изделий обуславливает
Необходимость разработки материалов высокой прочности с малой плотностью ( сплавы
магния, лития, бериллия). Изделия из этих материалов превосходят конструкции из стали и
титана. В современной технике широко используются газонаполненные материалы.
В некоторых материалах при тепловом воздействии обнаруживается «эффект памяти»
Слайд 3продолжение
«эффект памяти» – восстановление первоначальной формы пластически
деформированного образца в результате нагревания
на основе титана). Механизм этого явления обусловлен структурными
превращениями материала. Используется, в частности, при раскрытии
под действием солнечного тепла антеннах космических кораблей.
Переход авиации на реактивные двигатели придал актуальность
проблеме создания материалов, сохраняющих исходную прочность при
высоких температурах – решается путем переработки металлов в
гранулы методом высокоскоростной кристаллизации при сверхбыстром
охлаждении с последующим прессовании гранул в изделия.
Материалы, устойчивые к воздействию ядерного излучения и
окислительных сред – ядерные реакторы и МГД- генераторы.
Материалы для криогенной техники, сверхпроводящие материалы.
Сверхчистые материалы (ядерная энергетика, полупроводниковая
техника)
Композиционные материалы.
Слайд 4Атом
Атом – наименьшая частица химического элемента, обладающая его свойствами.
Он состоит из
научных представлений отведена роль первичных кирпичиков мироздания.
Протоны и нейтроны составляют положительно за ряженное ядро, а электроны
движутся вокруг ядра. Электрон – первая элементарная частица, открытая
человеком имеет массу покоя и является носителем элементарного
электрического заряда (кванта электричества). Ядро атома и окружающие его
электроны находятся в электростатическом и электромагнитном взаимодействии,
образуя устойчивую пространственную систему. Изолированный атом не имеет
заряда. В результате удаления или присоединения к нему электрона атом
превращается в ион (положительно или отрицательно заряженный).
Энергия атома может принимать лишь определенные (дискретные) значения,
называемые уровнями энергии (энергия атома квантуется). Уровни соответствуют
устойчивым состояниям атома и изменяются скачкообразно путем квантовых
переходов.Последние обусловлены воздействие на атомные частицы(атомы,ионы)
электромагнитного излучения. (Нейтрон – частица нестабильная)
Слайд 5продолжение
Кванты электромагнитного поля – фотоны – являются носителями
возможных при данной частоте поля энергии и импульса. Поглощая фотоны,
атомные частицы переходят в возбужденное состояние, из которого, испуская
фотон, переходят в состояние с меньшей энергией (на более низкий уровень
энергии).Уровень, соответствующий минимальной энергии атома,назван основным
остальные – возбужденными. Совокупность уровней представляют энергетический
спектр атома. Оптические спектры свободных (слабосвязанныз) атомов состоят из
отдельных спектральных линий и группируются в спектральные серии. Они несут
информацию об атомной структуре вещества.
Атомы разных химических элементов отличаются электронной конфигурацией,
т.е. распределением электронов по уровням энергии. Состояние электрона в атоме
характеризуется четырьмя квантовыми числами: главным квантовым числом «n»,
определяющим среднее удаление электрона от ядра (n = 1, 2, 3, …), орбитальным
«l», определяющим форму орбиты электрона в кулоновском поле ядра (l = 0, 1, 2, ..
(n – 1)), магнитным квантовым числом «m», определяющим проекцию момента
импульса на направление внешнего поля (m = -l, …,0, …+l) и спиновым квантовым
числом «S», определяющим собственный момент импульса электрона ( S = + 1/2,
-1/2). Энергия электрона в основном определяется n и l (более n).
Слайд 6продолжение
Согласному одному из законов квантовой механики (принцип Пвули) в одном атоме
любые
чисел. Совокупность возможных квантовых состояний с одинаковым главным
квантовым числом n составляет электронный слой, заполненный не более чем 2n²
электронами, который состоит из оболочек, характеризуемым значениями «l».
Приняты обозначения:
слои …. K, L, M, N, O, P, Q оболочки ….. s, p, d, f
n …………1, 2, 3, 4, 5, 6, 7 l………………..0, 1, 2, 3
Атомы элементов Периодической системы не имеют оболочек с l > 3. Чем
слабее электрон связан с ядром, тем выше уровень его энергии в
соответствующей оболочке.
Большинство химических и физических свойств атомов обусловлено структурой
его внешних электронных оболочек, в которых электроны связаны друг с другом
относительно слабо. Информацию о строении внутренних оболочек получают,
изучая взаимодействие атомов и быстрых частиц или фотонов высокой энергии.
Электростатическое взаимодействие атомов при сближении может привести к
перекрытию их электронных оболочек. Это проявляется в поляризуемости атомов
(способности атома приобретать дипольный момент), обусловлена смещением
электронов относительно ядер. Свойства ионов отличаются от свойств атомов.
Слайд 7ХИМИЧЕСКАЯ СВЯЗЬ
Под химической с вязью понимают взаимодействие между атомными частицами,
обусловленное
электронов независимым от движения ядер, можно представить образование
химической связи как результат притяжения положительно заряженных ядер к
электронному «облаку», сконцентрированному в межядерном пространстве.
Химическая связь - общее определение сил и взаимодействий, обуславливающих
существование двух- и многоатомных соединений – молекул, ионов, радикалов,
кристаллов. Главные особенности химической связи:
значение полной энергии многоатомной системы меньше, чем сумма энергий
несвязанных атомных частиц, из которых она образована;
2) электронные плотности (вероятные количества электронов в элементарном
объеме) заметно отличаются в поле сил химической связи и между несвязанными
атомными частицами, которые сближены на расстояние связи.
Природа химической с вязи определяется электрическим кулоновским
взаимодействием ядер и электронов, однако распределение электронов при
образовании химической связи подчиняется законам квантовой механики. При
образовании связи электроны распределяются так, что силы, стремящиеся
сблизить и оттолкнуть ядра, уравновешиваются.
Слайд 8продолжение
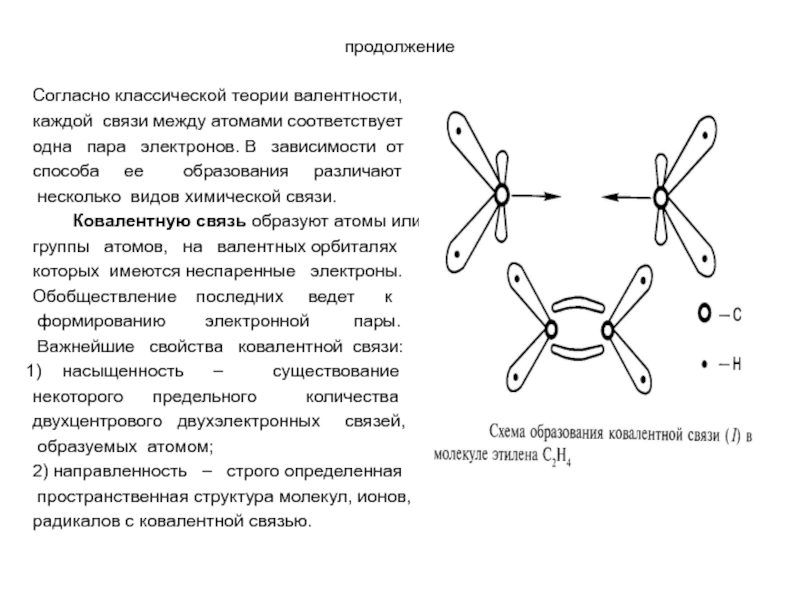
Согласно классической теории валентности,
каждой связи между атомами соответствует
одна пара
способа ее образования различают
несколько видов химической связи.
Ковалентную связь образуют атомы или
группы атомов, на валентных орбиталях
которых имеются неспаренные электроны.
Обобществление последних ведет к
формированию электронной пары.
Важнейшие свойства ковалентной связи:
насыщенность – существование
некоторого предельного количества
двухцентрового двухэлектронных связей,
образуемых атомом;
2) направленность – строго определенная
пространственная структура молекул, ионов,
радикалов с ковалентной связью.
Слайд 9продолжение
Так, в образовании ковалентной связи в молекуле этилена участвуют 4 электрона
атомов
Молекулярные орбитали имеют специфическую форму, которая определена
направленностью ковалентной связи. Электронное облако окружает оба ядра
атомов углерода.
Координационная связь (донорно-акцепторная)–химическая связь, реализуемая в
координационных (комплексных) соединениях. Последние образуются путем
присоединения к центральному атому (комплексообразователю) молекул и ионов -
Так называемых лигандов. Возникновение такой связи обусловлено передачей
электронной пары с целиком заполненной орбитали лиганда на вакантную
орбиталь центрального атома и образованием общей молекулярной орбитали.
Частным случаем координационной связи является водородная связь.
Разнообразие координационных связей обуславливает огромное разнообразие
структурных типов молекул координационных соединений, а также кристаллической
структуры твердых тел.
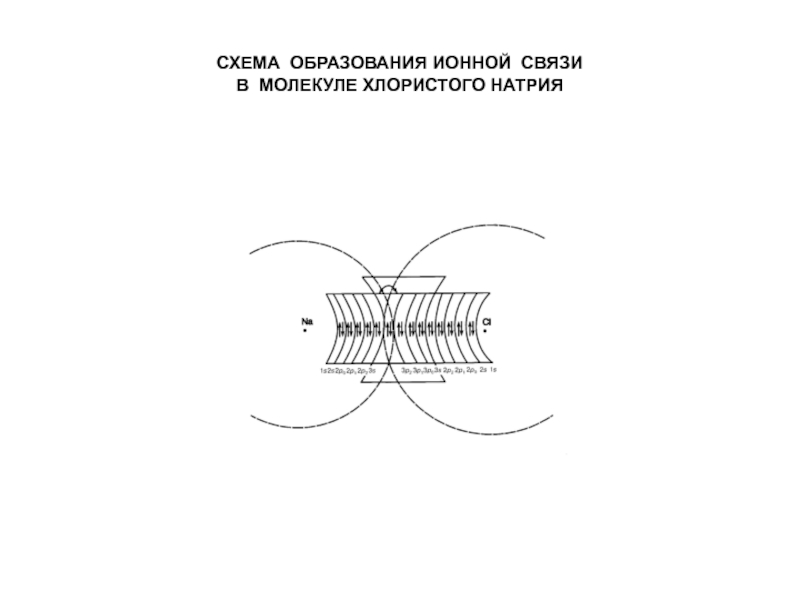
Ионная связь – химическая связь, энергия которой определяется преимущественно
кулоновским взаимодействием (притяжением) противоположно заряженных ионов.
Так, при образовании ионной связи в молекуле NaCl электроны переходят с
3s-орбитали атома Na на 3р-орбиталь атома Cl.
Слайд 11продолжение
Признаком соединений с ионной связью является свойство разлагаться на ионы
Полярных растворителях,т.к.энергия сольватации превышает энергию ионной связи.
Предельный случай делокализации электронных орбиталей – металлическая связь.
Она обусловлена перемещением валентных электронов металла во всем
пространстве, занятом его положительными ионами. Металлы можно представить
как ионной упорядоченный каркас, погруженные в «электронный газ», состоящий
из обобществленных электронов.
Прочность химической связи определяется ее энергией (от 10 до 1000 кДж/моль).
Слайд 12МОЛЕКУЛА
Молекула – наименьшая частица вещества, обладающая всеми его химическими
свойствами и
электрически нейтральна и, как правило, не имеет неспаренных электронов.
Молекулярный ион возникает в результате присоединения к молекуле или
отщепления от нее электрона. В состав молекулы входит от двух до многих сотен
и тысяч атомов (полимеры – макромолекулы). Соответственно размеры молекул
от десятых долей нанометра до нескольких микрон. Структура молекулы каждого
вещества не зависит от способа его получения. Состав молекулы передает брутто-
формула (H2O, CH4, HCl и т.п.)., которую устанавливают химическим анализом.
Структурные формулы отражают последовательность и порядок связей между
атомами. Каждая молекула имеет определенную пространственную форму. Форма
молекул определяется электрическим зарядом и размером ионов (ионные
соединения) или конфигурацией электронных орбиталей (ковалентные связи).
Определенная и более сложная геометрическая структура характерна для молекул
с координационными связями.
Молекулы с одинаковой брутто – формулой могут различаться расположением
атомов в пространстве.
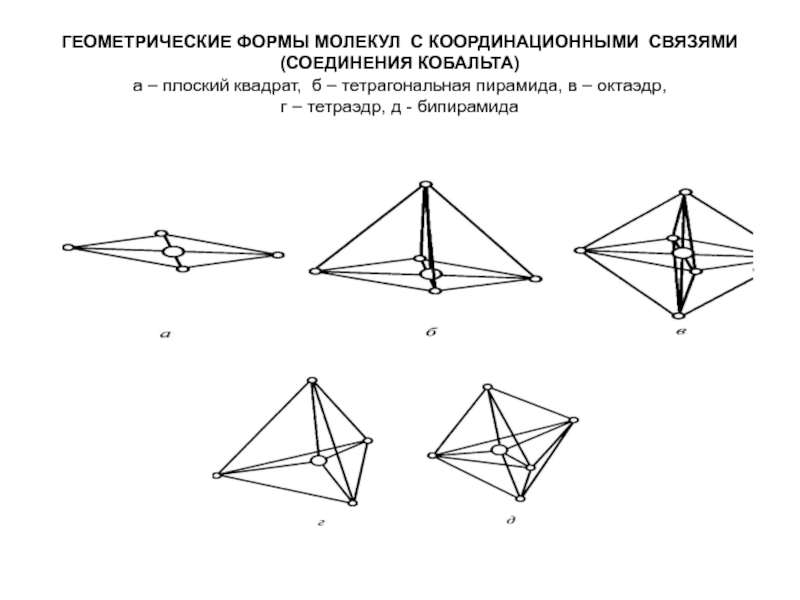
Слайд 13ГЕОМЕТРИЧЕСКИЕ ФОРМЫ МОЛЕКУЛ С КООРДИНАЦИОННЫМИ СВЯЗЯМИ (СОЕДИНЕНИЯ КОБАЛЬТА) а – плоский квадрат, б
Слайд 14продолжение
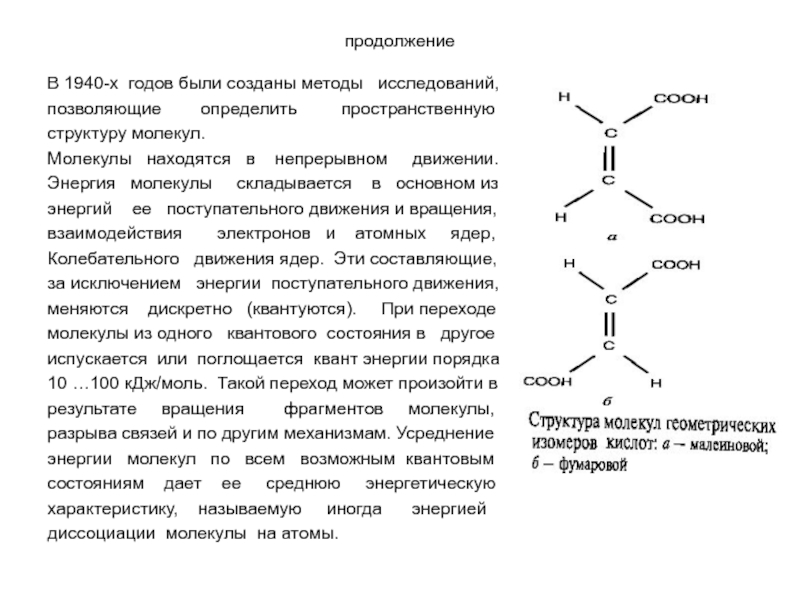
Изомерия - явление, заключающееся в
существовании
одинаковых по составу и молекулярной массе,
Но отличающихся строением и вследствие
этого физическими и химическими свойствами
( соединения - изомеры ). Различают
структурные и пространственные изомеры.
Явление, когда два (или более) структурных
изомера самопроизвольно переходят друг в
друга и между ними существует неустойчивое
равновесие, называется таутометрией. При
установившемся равновесии вещество
содержит одновременно молекулы
таутомеров в определенном соотношении.
Пространственные формы молекул –
конформации - могут возникнуть в
результате вращения фрагментов молекулы
вокруг простых связей.
Слайд 15продолжение
В 1940-х годов были созданы методы исследований,
позволяющие
структуру молекул.
Молекулы находятся в непрерывном движении.
Энергия молекулы складывается в основном из
энергий ее поступательного движения и вращения,
взаимодействия электронов и атомных ядер,
Колебательного движения ядер. Эти составляющие,
за исключением энергии поступательного движения,
меняются дискретно (квантуются). При переходе
молекулы из одного квантового состояния в другое
испускается или поглощается квант энергии порядка
10 …100 кДж/моль. Такой переход может произойти в
результате вращения фрагментов молекулы,
разрыва связей и по другим механизмам. Усреднение
энергии молекул по всем возможным квантовым
состояниям дает ее среднюю энергетическую
характеристику, называемую иногда энергией
диссоциации молекулы на атомы.
Слайд 16продолжение
Молекулы электронейтральны, однако если «центры тяжести» положительных и
отрицательных зарядов
собственным электрическим дипольным моментом. Неполярные молекулы
поляризуются во внешнем электрическом поле. В подавляющем большинстве они
диамагнитны Парамагнитными молекулами являются молекулярные радикалы
(молекулы, имеющие неспаренные электроны).
В результате взаимодействия одинаковых или близких по природе молекул
возникают более сложные образования – ассоациты (димеры, тримеры и т.п.).
Изучение структуры и свойств молекул имеет фундаментальное значение для
естествознания в целом и для материаловедения особенно.
Слайд 17ФАЗОВОЕ СОСТОЯНИЕ ВЕЩЕСТВА
Физические свойства веществ можно изучать на основе анализа
них преобразований энергии. Состояние термодинамической системы, в которое
Она самопроизвольно приходит в течение достаточно большого промежутка
времени при неизменных внешних условиях, называют равновесным. Фаза –
термодинамически равновесное состояние вещества, отличающееся свойствами от
других возможных равновесных состояний того же вещества.Иногда неравновесное
(метастабильное) состояние вещества также называют фазой (метастабильной).
Любой однофазный материал характеризуется отсутствием поверхностей раздела
между составляющими его структурными образованиями, т.е. является гомогенным
Гетерогенный материал содержит как минимум две фазы.
Фазовый переход – переход вещества из одной фазы в другую при изменении
внешних условий. Значение температуры, давления, напряженности магнитного ,
электрического поля или другой физической величины, при которой происходит
фазовый переход называют точкой перехода. Различают фазовые переходы двух
родов.
Фазовые переходы I –го рода – сопровождаются скачкообразным изменением
термодинамичческих характеристик вещества (плотности, концентрации и др.) при
непрерывном изменении его внешних параметров.
Слайд 18продолжение
В веществе выделяется или поглощается определенное количество
называемое теплотой фазового перехода. К переходам I рода относят испарение и,
конденсацию, плавление и затвердевание, сублимацию и конденсацию в твердой
фазе, некоторые структурные переходы в твердых телах.
В отсутствии внешних полей и химических реакций состояние фазы, содержащей
k- компонентов, определяется (k + 1) независимыми параметрами: температурой,
давлением и (k – 1) молекулярными долями компонентов. Функции этих
параметров, характеризующие фазу, называют термодинамическими
параметрами. К последним относят так называемый изобарно – изотермический
потенциал, или потенциал Гиббса: G = H - TS, где H–энтальпия (теплосодержание)
H = U + pV (U – внутренняя энергия системы, p- давление, V – объем системы); T –
Температура; S – ‘энтропия или мера необратимой рассеянной энергии: dS = δQ/T;
где dS – дифференциал энтропии, δQ – количество теплоты, сообщенное системе
в изотермическом процессе.
При температуре абсолютного нуля и фиксированном давлении термодинамически
равновесной является фаза с минимальным значением G. В точке перехода фазы
с одинаковыми значениями G находятся в равновесии.
Слайд 19продолжение
При фазовых переходах I рода может возникать метастабильная фаза, в
вещество может длительное время, не переходя в устойчивую фазу. Например,
жидкость можно нагреть выше точки кипения или переохладить ниже точки
замерзания.Это связано с особенностями кинетики фазовых переходов. Последние
начинаются с возникновения зародышей новой фазы – появления пузырьков пара
при кипении, микрокристалликов при кристаллизации и т.п. Для образования
Зародышей требуется энергия, которая расходуется на создание поверхностей
раздела фаз. Это может задержать переход материала из метастабильной фазы в
более устоичивую.
При фазовых переходах II рода плотность и термодинамические функции веществ
непрерывны, а скачок испытывают производные этих функций по давлению и
температуре, например теплоемкость при постоянном давлении, магнитные
фазовые переходы, переход материала из нормального состояния в
сверхпроводящее и пр.
Фазовые переходы первого рода часто являются агрегатными. Признаком того
или иного агрегатного считают значение величины ε( р, Т) – отношение средней
потенциальной энергии взаимодействия молекул в веществе к их кинетической
энергии.
Слайд 20Агрегатные состояния
Проблема структуры макротел связана с агрегатным состоянием объекта.
агрегатное состояние вещества, в котором частицы не вязаны или слабо связаны
силами взаимодействия и хаотически движутся, заполняя весь объем. Для газов
ε( р, Т) << 1, при этом тело не обладает определенной формой, и заполняет весь
объемом. Ионизированный газ, в котором плотности положительных зарядов и
отрицательных практически одинаковы, - плазму - считают четвертым агрегатным
состоянием вещества. Газ считают идеальным, если силами межмолекулярного
взаимодействия можно пренебречь. Для сжижения газов используют эффект
охлаждения, происходящий при их расширении без теплообмена с окружающей
средой. Если газовая фаза находится в равновесии с жидкой или твердой фазой
того же вещества то это насыщенный пар.
Жидкости – вещества, сочетающие свойства газов и твердых тел. Для них ε( р, Т)
≈ 1. Тепловое движение молекул (атомов) жидкости представляет собой сочетание
сочетание малых колебаний около положения равновесия и перескоков из одного
положения равновесия в другое.Жидкости практически не сжимаемы. Их испарение
фазовый переход 1 рода и характеризуется энергией – теплотой парообразования.
По мере охлаждения движение молекул жидкости замедляется, а когда они
фиксируются в определенных положениях, жидкость превращается в твердое тело
Слайд 21продолжение
Процесс плавления характеризуется теплотой плавления. Внутри жидкости каждая
молекула испытывает притяжение
сила равна нулю. Силы притяжения, приложенные к молекуле, лежащей на поверх –
ности жидкости, не скомпенсированы притяжением сверху, поэтому поверхность
жидкости на границе с газом подобна натянутой пленке. Поверхностное натяжение
жидкости – это работа, которую нужно совершить, чтобы увеличить при данной тем-
пературе на единицу площадь поверхность поверхности раздела жидкости с ее на-
сыщенным паром. Смачивание – явление, возникающее при соприкосновении жид-
кости с поверхностью твердого тела или другой жидкости. Оно является результа-
том молекулярного взаимодействия на границе раздела фаз и обуславливает расте-
кание жидкости по поверхности сопряженного тела, искривление ее свободной по -
верхности вблизи границы соприкосновения (мениск), пропитывание жидкостью по –
ристых твердых тел и порошков и т.д.
Вязкость – или внутреннее трение – свойство текучих веществ оказывать сопротив-
ление перемещение одной их части относительно другой. Текучесть – величина,
обратная вязкости.
Слайд 22твердое тело
.Твердое тело характеризуется стабильностью форм, т.к. образующие его атомы совер-
шают лишь малые(тепловые) колебания около фиксированных положений равновесия.
Для твердых тел ε( р, Т) >> 1. Твердые тела относятся к системам сильно взаимодейст-
вующих частиц. Физические свойства твердых тел в значительной мере определяются
степенью пространственного упорядочения их частиц.
Кристаллы – твердые тела с трехмерной периодической атомной структурой, имеющие
форму правильных симметричных многогранников. Кристаллизация, т.е. образование
кристаллов происходит при нарушении термодинамического равновесия в маточной
среде: жидкостях (раствор или расплав), газовой фазе (пар) или твердое тело.
Кристаллическая решетка – регулярное расположение в кристаллах частиц (атомов,
ионов, молекул), характеризующееся периодической повторяемостью в трех измерени-
ях. При этом достигается уравновешение сил притяжения и отталкивания, соответству-
ющее минимуму потенциальной энергии твердого тела. Для веществ в конденсирован-
ном состоянии (находящихся в жидком и твердом агрегатном состоянии) характерна
согласованность в расположении соседних частиц – ближний порядок, который
проявляется на расстояниях, сравнимых с межатомным. Кристаллические вещества
имеют дальний порядок – строгую повторяемость во всех направлениях одного и того
же структурного элемента на протяжении сотен и тысяч периодов кристаллической ре-
шетки. Представление о строении кристалла дает элементарная ячейка - часть атом-
ной структуры кристалла, путем трансляции которой (т.е. переноса в пространстве пара-
ллельно самой себе построить всю кристаллическую решетку.
Слайд 23продолжение
Ребра элементарных ячеек обозначают
буквами «a, b, c» и называют периода-
ми кристаллической
тороной форме) векторами трансляции.
Каждая атомная плоскость кристалли-
ческой решетки, пересекаясь с осями
координат, отсекает на них отрезки, со-
ответствующие периодам решетки. Ве-
личины, обратные длине этих отрезков,
обозначают буквами h, k, l и называют
кристаллографическими индексами
граней и атомных плоскостей. Большин-
ство кристаллов имеет грани со значени-
ями индексов от 0 до 3, например (100),
(110), (311). Выбор осей координат прои-
зводят по особым правилам а соответст-
вии с симметрией кристаллов и правила-
ми преобразований симметрии (поворо-
тов,отражений,параллельныхпереносов пр
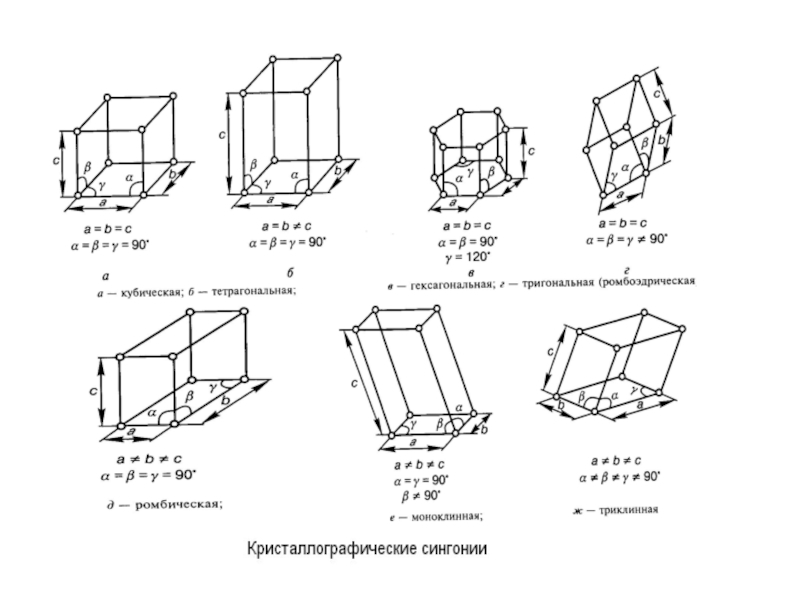
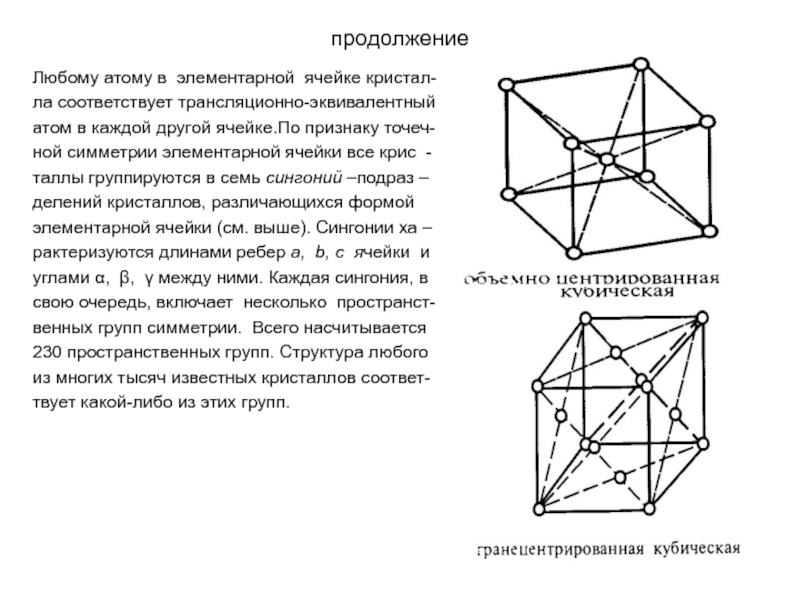
Слайд 25продолжение
Любому атому в элементарной ячейке кристал-
ла соответствует трансляционно-эквивалентный
атом в каждой
ной симметрии элементарной ячейки все крис -
таллы группируются в семь сингоний –подраз –
делений кристаллов, различающихся формой
элементарной ячейки (см. выше). Сингонии ха –
рактеризуются длинами ребер a, b, c ячейки и
углами α, β, γ между ними. Каждая сингония, в
свою очередь, включает несколько пространст-
венных групп симметрии. Всего насчитывается
230 пространственных групп. Структура любого
из многих тысяч известных кристаллов соответ-
твует какой-либо из этих групп.
Слайд 26продолжение
Твердые материалы являются, как правило, поликристаллическими, т.е. состоят из
множества беспорядочно
кристаллитов. Крупные одиночные кристаллы называют монокристаллами. При
неравновесной кристаллизации форма кристаллов отклоняется от формы правиль-
ного многогранника. Эту особенность используют для выращивания монокристаллов
повторяющих форму технических изделий – труб, пластин и т.п.
Для кристаллов характерно упорядоченное расположение атомов, ионов или
молекул; однако оно, как правило, не совершенно из-за разнообразных дефектов
кристаллов.Нарушение порядка неустранимо, что связано с непрерывным тепловым
колебанием. Элементов решетки. Частоты колебаний зависят только от массы эле -
ментов решетки и от действующих между ними сил, амплитуда колебаний растет с
ростом температуры.Колебания не прекращаются даже при абсолютном нуле, ибо
материя и движение неотделимы.
Элементы кристаллической решетки в разных направлениях находятся на разном
расстоянии, поэтому физические свойства в разных направления различны -
анизотропия кристаллов. При нагревании кристаллы расплавляются. Четко опреде-
определенная точка плавления–это температура, при которой амплитуда колебаний
элементов решетки достигает такой величины и соседние элементы решетки начи-
начинают сталкиваться настолько сильно, что кристаллическая решетка
разрушается. Возникает жидкость. Анизотропия, как правило, иччезает.
Слайд 27Особое положение занимает поверхность. Свойства поверхности отличаются от
свойств
ния технологии переработки материалов и повышения работоспособности техниче-
ских изделий.
Полиморфизм – свойство некоторых веществ существовать в нескольких кристал-
лических модификациях с разной структурой.
Устойчивость кристаллической структуры зависит от типа связей между частица-
ми в кристалле
Существуют состояния, отличающиеся от классических агрегатных состояний.
Стеклообразное состояние – промежуточное положение между кристаллом и
жидкостью (нет дальнего порядка, но твердое) – стекло, многие окислы и пр.
Промежуточное состояние между кристаллическим и газообразным (положение мо-
лекул упорядочено, но они совершают и вращательное движение при некоторых
температурах).
Сложные тела могут возникать путем увеличением числа атомов в молекулах –
макромолекулы (белок, целлюлоза, нейлон и т.п.) объединяют тысячи и миллионы
атомов. С увеличением числа атомов в молекуле проявляются качественно новые
физические и химические свойства. Макрамолекулярные вещества не относятся ни
к одному из агрегатных состояний.
Слайд 28Типы кристаллических решеток
Исходя из вида элементов решетки действующих между ними
сил
Ионные кристаллы (ионная решетка) - содержит в качестве
элементов решетки ионы (положительные и отрицательные) с
соответствующим кулоновским взаимодействием.
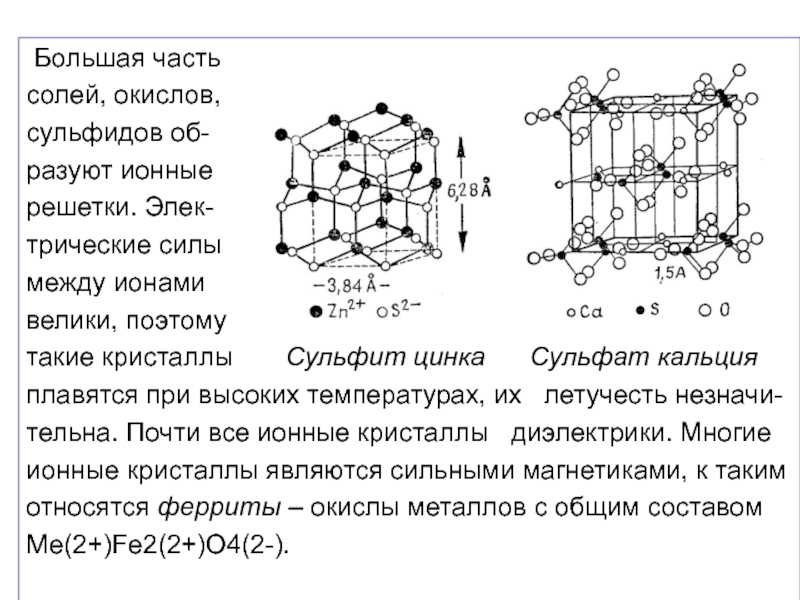
Слайд 29 Большая часть
солей, окислов,
сульфидов об-
разуют ионные
решетки. Элек-
трические силы
между ионами
велики, поэтому
такие
плавятся при высоких температурах, их летучесть незначи-
тельна. Почти все ионные кристаллы диэлектрики. Многие
ионные кристаллы являются сильными магнетиками, к таким
относятся ферриты – окислы металлов с общим составом
Ме(2+)Fe2(2+)O4(2-).
Слайд 302. Атомные кристаллы (атомная решетка) –
нейтральных атомов неметаллических элементов, удержи -
вающих друг друга силами ковалентной связи. К таким крис –
таллам принадлежат алмаз, графит. В
решетке алмаза каждый атом углерода
окружен четырьмя другими атомами,
находящимися от него на одинаковом
расстоянии (~1,54 Ǻ), так что эти 4 атома
образуют вершины тетраидра в центре Алмаз Графит
которого находится рассматриваемый атом. Каждый из этих
четырех атомов находится в центре другого тетраидра. В ал-
мазе не имеется молекул, так как все атомы углерода равно-
равномерно связаны между собой.
Связь между атомами углерода в плоскости такая же боль -
шая, как и в алмазе.
Слайд 313. Молекулярные кристаллы (молекулярная решетка) – эле-
ментами решетки
Ван-дер-Ваальса или силами водородной связи. Молекулы,
находящиеся в узлах решетки, относительно самостоятельны
и связаны между собой слабыми
Ван-дер-Ваальсовыми силами, а
иногда водородными связями.
Поэтому кристаллы с молекуляр-
ной решеткой имеют довольно Двуокись Карбамид
низкую температуру плавления и углерода CO(NH(2))(2)
легко испаряются. Имеются молекулярные кристаллы, эле -
менты которых связаны ориентированными весьма слабыми
силами химической связи.
К таким веществам относится, в частности, лед. Его молеку –
лы соединены между собой посредством водородных связей.
Молекулы воды в кристалле упакованы неплотно, но даже
В столь рыхлой структуре связи, исходящие из атомов
кислорода, ориентированы.
Слайд 32
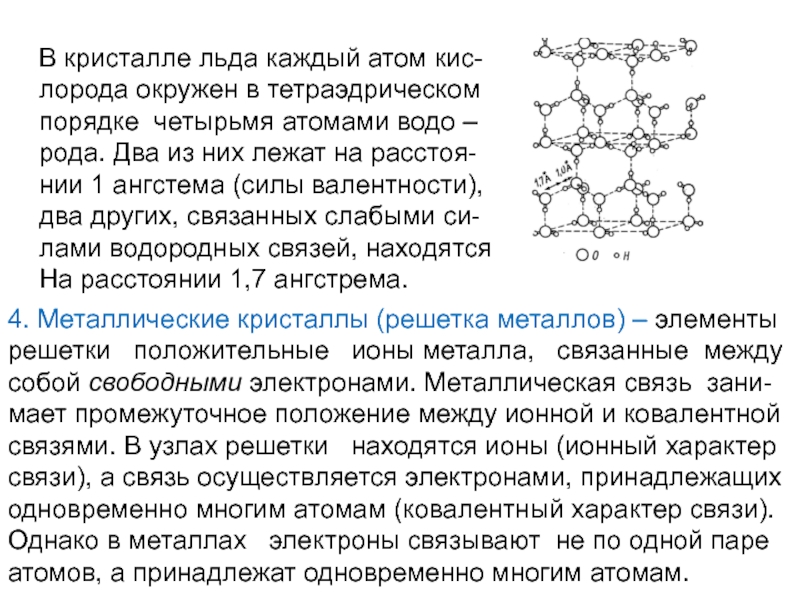
4. Металлические кристаллы (решетка металлов) – элементы
решетки положительные
собой свободными электронами. Металлическая связь зани-
мает промежуточное положение между ионной и ковалентной
связями. В узлах решетки находятся ионы (ионный характер
связи), а связь осуществляется электронами, принадлежащих
одновременно многим атомам (ковалентный характер связи).
Однако в металлах электроны связывают не по одной паре
атомов, а принадлежат одновременно многим атомам.
В кристалле льда каждый атом кис-
лорода окружен в тетраэдрическом
порядке четырьмя атомами водо –рода. Два из них лежат на расстоя-
нии 1 ангстема (силы валентности),
два других, связанных слабыми си-
лами водородных связей, находятся
На расстоянии 1,7 ангстрема.
Слайд 33Дефекты кристаллической решетки.
В идеальном кристалле элементы решетки расположены в
строгом порядке,
такие кристаллы не существуют в действительности. Кроме
беспорядка, связанного с тепловым движением, в реальном
кристалле неизбежны отклонения другого рода, нарушающие
порядок и они означают уже настоящие дефекты решетки.
Особо важную роль играют незанятые узлы решетки (вакант-
ные узлы, дырки). За их образование в первую очередь также
ответственно тепловое движение (энергия отдельных элемен-
тов решетки становится достаточно большой и они вырыва –
ются из предписанного им места, оставив после себя «дырку»
(пустоту).
Слайд 34Если дефект образуется вблизи
поверхности кристалла, то он
достигает и
участие в дальнейшем росте
кристалла (дефект по Шоттки).
Кристалл NaCl
Если элемент решетки покидает
свое место внутри кристалла, то
он вклинивается между другими
элементами решетки, вызывая
образование дырки и межреше –
точное замещение (дефект по Кристалл AgBr
Френкелю).
Дырки могут блуждать, с поверхности могут переходить в
глубину кристалла, создавая т.н. дефекты конфигурации.
Слайд 35
Дефекты решетки возникают также в том случае, если в
отдельных ее узлах или между ними находятся посторонние
атомы или ионы. В т.н. бертоллидах значительное отклонение
от стехиометрии не оказывает скачкообразного изменения
на химические свойства в отличии от дальтонидов. Так в хло-
ристом натрии при отличии отношения масс его составных
частей от 22,989 : 35,453 кроме свойств соли обнаруживаются
свойства металлического натрия или хлора.
Отклонения от стехиометрии имеют существенное значение
для кристаллов металлических сплавов.
Дырки и особенно межрешетчатые включения локально иска-
жают кристаллическую решетку, что влияет на механические
свойства, окраску и т.д.
Слайд 36Наряду с локальными дефектами решетки существуют т.н.
дислокации (замещения), образующиеся по
-либо направлению вследствие
неправильного положения мно –
гих элементов решетки (линей-
ные дефекты решетки). Дисло-
кации возникают в процессе крис-
таллизации под влиянием загряз- Схемы различных
нений, а также при деформации смещений в одной
кристалла. Реальные кристаллы плоскости решетки
состоят из мозаичных блоков, зерен (из-за дислокаций), нес –
колько отличающихся по ориентации, что существенно влия-
ет на механические свойства. Многие твердые вещества в
действительности являются поликристаллическими.
Слайд 37В случае образования сплавов могут реализо-
ваться и другие точечные
лической решетки, например, химические
примеси. Это инородные атомы.
Если эти атомы замещают атомы основного,
то они называются примесями замещения
(рисунки «а» и «б»). Если они внедряются в
Промежутки между узлами кристаллической
решетки, то их называют примесью внедрения
(рисунок «в»).
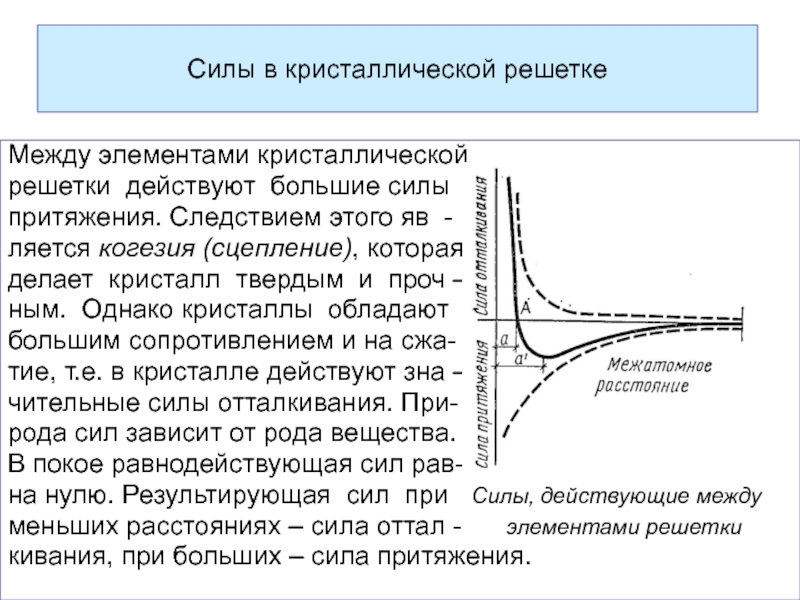
Слайд 38Силы в кристаллической решетке
Между элементами кристаллической
решетки действуют большие силы
притяжения. Следствием этого
ляется когезия (сцепление), которая
делает кристалл твердым и проч –
ным. Однако кристаллы обладают
большим сопротивлением и на сжа-
тие, т.е. в кристалле действуют зна –
чительные силы отталкивания. При-
рода сил зависит от рода вещества.
В покое равнодействующая сил рав-
на нулю. Результирующая сил при Силы, действующие между
меньших расстояниях – сила оттал - элементами решетки
кивания, при больших – сила притяжения.
Слайд 39С увеличением межатомного расстояния сила притяжения
растет только
больших α’ сила притяжения уменьшается и этой силы дос –
точно, чтобы разрушить кристалл - прочность на разрыв.
Как видно из рисунка, кривая равнодействующей силы, дейст-
вующей на атомы, ассиметрична, т.е. сила, действующая на
атом, больше силы притяжения. Вследствие этого средняя
точка колебаний с возрастанием их амплитуды сдвигается из
положения А в сторону больших расстояний между атомами,
т.е. температурное расширение кристаллов – следствие ас -
симетрии кривой результирующей силы. Чем ниже температу-
ра, тем меньше ассиметрия. Коэффициент линейного расши -
рения (β) тем больше, чем меньше крутизна кривой. Ясно, что
чем больше β, тем ниже температура плавления кристалла.
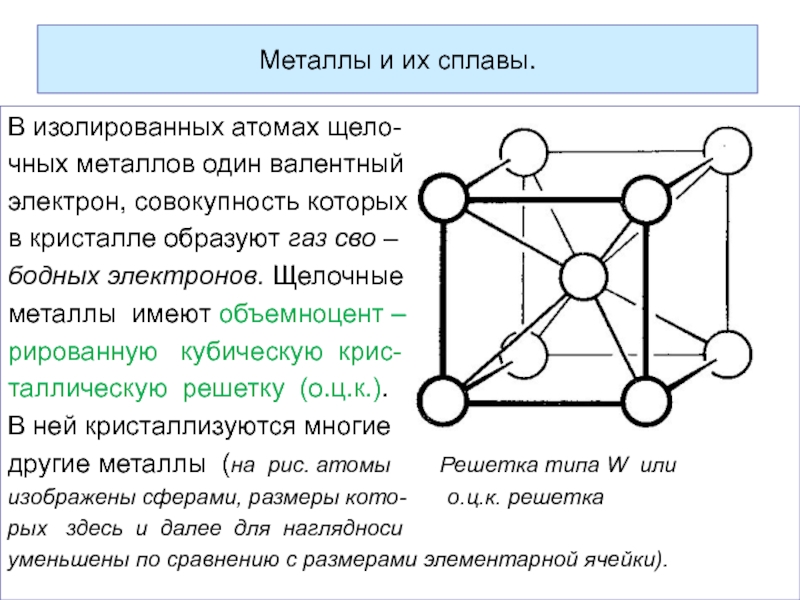
Слайд 40Металлы и их сплавы.
В изолированных атомах щело- -
чных металлов один валентный
электрон,
в кристалле образуют газ сво –
бодных электронов. Щелочные
металлы имеют объемноцент –
рированную кубическую крис-
таллическую решетку (о.ц.к.).
В ней кристаллизуются многие
другие металлы (на рис. атомы Решетка типа W или
изображены сферами, размеры кото- о.ц.к. решетка
рых здесь и далее для наглядноси
уменьшены по сравнению с размерами элементарной ячейки).
Слайд 41
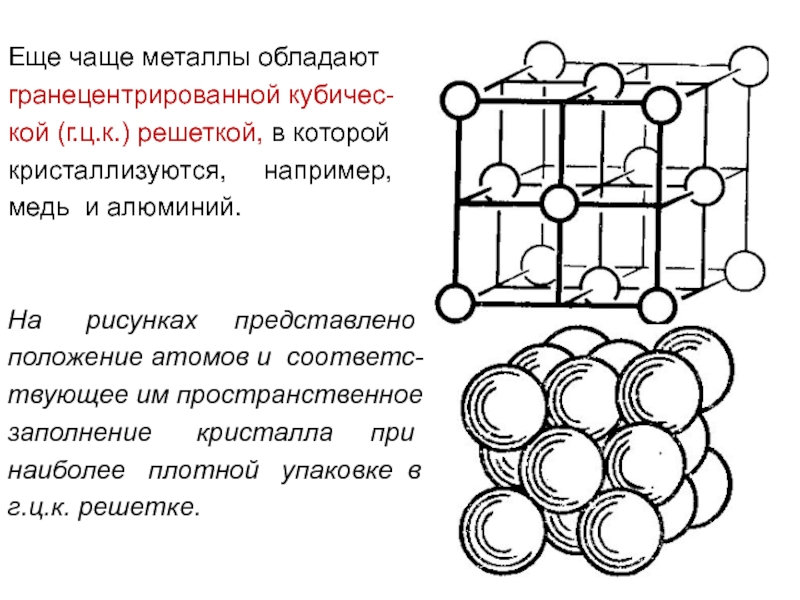
Еще чаще металлы обладают
гранецентрированной кубичес-
кой (г.ц.к.) решеткой, в которой
кристаллизуются,
медь и алюминий.
На рисунках представлено
положение атомов и соответс-
твующее им пространственное
заполнение кристалла при
наиболее плотной упаковке в
г.ц.к. решетке.
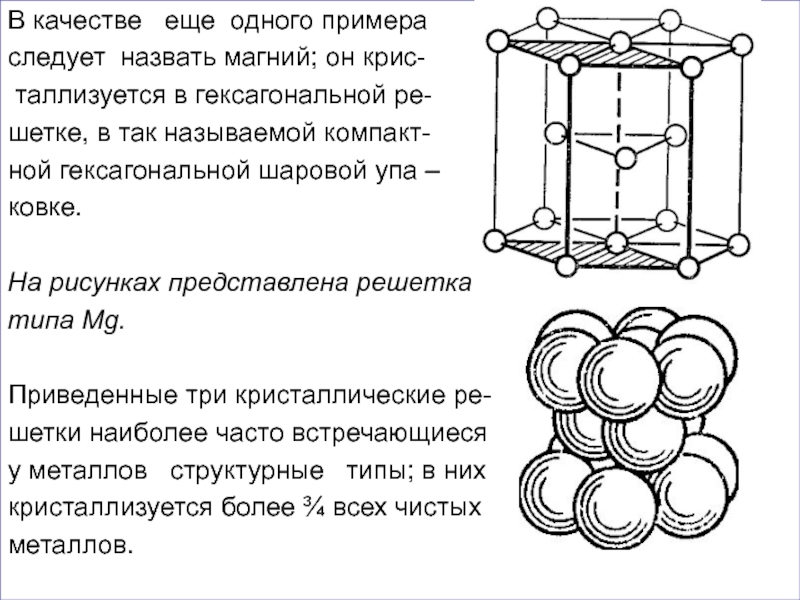
Слайд 42В качестве еще одного примера
следует назвать магний; он крис-
таллизуется
шетке, в так называемой компакт-
ной гексагональной шаровой упа –
ковке.
На рисунках представлена решетка
типа Mg.
Приведенные три кристаллические ре-
шетки наиболее часто встречающиеся
у металлов структурные типы; в них
кристаллизуется более ¾ всех чистых
металлов.
Слайд 43Решающее значение для технического применения металлов
имеет их исключительная способность образовывать
Сплавы позволяют получить такой широкий спектр свойств,
который едва ли достижим другим способом.
Сплав – смесь нескольких металлов, образующих связное те-
ло (смесь порошков – не сплав). В отношении растворимости
два предельных случая:
1. Компоненты сплава не образуют твердых растворов (гете-
рогенная смесь). Пример: медь – свинец.
2. Компоненты сплава обладают неограниченной раствори –
мостью (гомогенный сплав – твердый раствор).
Возможно образование соединений с кристаллической решет-
кой, отличной от решеток исходных компонентов. В этом слу-
чае – интерметаллические соединения или промежуточные
Фазы. Пример: PbMg(2).
Слайд 44ТЕРМОДИНАМИЧЕСКОЕ РАВНОВЕСИЕ
ОБЩИЕ УСЛОВИЯ РАВНОВЕСИЯ
Многие металлы и сплавы в зависимости от внешних
могут иметь различные кристаллические решетки и разную
степень дефектности. Каково состояние системы при данных
условиях?
Под системой будем понимать совокупность веществ, в дан –
ном случае металлов, находящихся в физико-химическом вза-
имодействии. Любую систему можно разделить на произволь-
но малые объемы. Если отдельные объемы не различаются
по составу и свойствам, систему называют гомогенной, в про-
тивном случае она будет гетерогенной. Взятые в отдельности
гомогенные области называют фазами. Гомогенная область
всегда однофазна (слиток меди, твердый раствор Cu – Al.
Слайд 45Гетерогенная смесь всегда многофазна ( смесь жидкой и твер
дой меди
нельзя обнаружить связи между числом фаз системы и чис –
лом ее компонентов.
Состояние системы считается заданным, если известны хи –
мический состав, давление Р и температура Т. Обозначим че-
рез К число компонентов, а через Ф – число фаз. Такие вели-
чины, как объем V, масса М, энергия U, энтропия S, которые
пропорциональны количеству вещества, называют экстенси-
вными величинами, те же, которые не удовлетворяют этому
условию, например, плотность ρ или температура Т – интен –
сивные величины. Частное двух экстенсивных (М/V = ρ) – ин-
тенсивная величина. Экстенсивная величина для гетерогенно
й смеси получается суммированием составляющих:
Ψ = ΣΨi
Слайд 46Как показывает термодинамическое рассмотрение, для рав –
новесия недостаточно, чтобы какая-нибудь из
тояния (скажем, энергия или энтропия) имели экстремальное
значение. Однако принцип экстремальности применим в том
случае, когда на сравниваемые состояния наложены опреде-
ленные ограничения (например, состояния с одинаковым дав-
лением и постоянной температурой). При таких ограничени –
ях равновесное состояние системы определяется условием
минимума термодинамического потенциала Гиббса:
G = U + pV – TS = H – TS,
Н – этальпия. Следовательно, в системе с данным количест-
вом вещества могут происходить лишь такие такие процессы,
при которых термодинамический потенциал не растет. Они
прекращаются, как только G достигает минимума – это озна-
чает наступление термодинамического равновесия.
.
Слайд 47В случае, если заданы не «р» и Т, а используются другие
менные, целесообразно применять другие функции. Напрмер,
для заданных V и Т используют F – свободную энергию (Гель-
гольца): F = U – TS. Найдем дифференциал обеих частей:
dF = dU - TdS - SdT ≤ - pdV – SdT.
Неравенство dU - TdS ≤ - pdV – результат совместного анали-
за 1 и 2 Начал термодинамики. Поскольку dV = dT = 0, то и
dF = 0 и, следовательно, F → min. Это означает, что термо-
динамическому равновесию из всех состояний при данных V и
Т отвечает лишь то, которое обладает минимальной свобод –
ной энергией.
Слайд 48МОДЕЛИРОВАНИЕ СТРУКТУРЫ МАТЕРИАЛОВ
Моделирование – метод научного исследования, состоящий в замене изучаемого
объекта ему подобным, но более простым объектом – моделью. Разработка новых
материалов, как правило, начинается с построения моделей их структуры на атом-
ном, молекулярном и макроуровнях. Различают функциональное моделирование
материалов, моделирование их атомно-молекулярной структуры и структуры компо
зитов на нано-, микро- и макроуровнях. В порядке усложнения эксплуатационных
функций материалы образуют ряд: однофункциональные – многофункциональные
– активые - «умные». Многофункцмональные материалы выполняют в машинах не
одну, а несколько функций. Например, бронза является конструкционным и трибо-
техническим материалом в машиностроении. Многие пластмассы используют для
защиты металлических деталей от коррозии и для создания в изделии электричес-
кой изоляции. Активные материалы, выполняя в машинах присущие обычным тех-
ническим материалам функции, оказывают на сопряженные части машин и окружа-
ющую среду воздействия физической, химической или биологической природы.
Примеры активных материалов. Магнитострикция – изменение размеров и формы
кристаллического тела при намагничивании. Магнитострикционные металлические
материалы, проявляющие эффект Виллари, обратный магнитострикции, являются
активными материалами.При большоим механическом нагружении в них генериру -
ются магнитные поля,которые сигнализируют о высоких уровнях напряжений в узле
Слайд 49Химическую активность проявляет фильтрующий материал на основе углеродной ткани, про-
питанной комплексонами.
координационные соединения. Активный материал механически улавливает содержащиеся
в фильтруемой жидкости твердые частицы загрязнений и химически связывает сольватиро -
ванные в нем ионы тяжелых металлов, которые являются очень опасны в экологическом
смысле и трудноуловимы. Пример биологически активного материала – носитель микроор –
ганизмов в биологических фильтрах.«Умные» материалы – это активные материалы с обрат-
ной связью. Обратная связь – воздействие нового состояния окружающей среды,измененной
материалом, на интенсивность изменяющихся свойств. Одна из современных идей созда-
ния «умного» материала состоит в предании ему способности производить самодиагности –
ку (мониторинг) и осуществлять самовосстановление. Так, при обнаружении микротрещины
в «умном» материале срабатывает механизм самовосстановления путем перераспределе -
ния вещества. Разрабатываются методы самозалечивания микротрещин с помощью частиц
нанометрового диапазона. Моделирование физико-химической структуры материала бази –
руется на методах квантовой механики. Основы квантовой механики были заложены в нача –
ле ХХ века. Планк, Эйнштен, Бор показали, что электроны и атомы имеют стационарные и
возбужденные состояния, переходы между которыми сопровождаются излучением или пог –
лолощением квантов энергии (света). В 1924 г. Луи де Бройль описывать свободное движе –
ние частицы (с энергией Е и импульсом Р) той же функцией ψ(r, t) = C exp I (Pr – Et) / ħ, что и
перемещение волны в пространстве и времени t. Здесь r –радиус–вектор частицы, i –мнимая
единица, С – постоянный множитель, ħ – постоянная Планка. Забегая вперед, заметим, что
тем самым он предсказал дифракцию таких частиц при рассеянии на кристаллах. В 1926 г.
Шредингер разработал дифференциальное уравнение, решением которого являются ψ(r, t) ,
Слайд 50получивших название волновых функций и уровни энергий исследуемой системы частиц.
Были разработаны методы квантовой химии, составившие основу моделирования материа-
лов. Гайтлер и Лондон на примере молекулы водорода дали квантово-механическую интер-
претацию ковалентной связи. Их подход в дальнейшем получил название метода валентных
связей. С его помощью удалось получить приближенные решения уравнений Шредингера
для многоатомных молекул. Позднее был разработан метод молекулярных орбиталей, кото-
рый широко применяется при моделировании материалов, позволяя рассчитать волновые
функции, энергетические уровни и свойства молекул. Одновременно Хартри и Фок разрабо-
тали метод самосогласованного поля. Название этого метода связано с тем, энергетическое
состояние каждой частицы, входящей в молекулу,определяется усредненным полем,которое
создается всеми остальными частицами, т.е. состояние молекулы согласуется с состоянием
ее атомов, ионов, электронов. Был разработан метод конфигурационного воздействия. С его
помощью можно решить уравнение Шредингера для молекулы, находящейся в основном и
возбужденном состоянии. Наконец, была разработана теория кристаллического поля,соглас-
но которой низшие по энергии состояния молекулы описываются как состояния одного атома
находящегося в электрическом поле, созданном другими частицами. Прогресс вычислитель-
ной техники стимулировал развитие методов квантовой химии и позволил с высокой точно-
стью прогнозировать свойства «проектируемых» молекул.
Основы математических методов квантовой химии и их применение в компьютерных экспе-
риментах составляют содержание специальных курсов для студентов соответствующих спе-
циальностей.
Моделирование композиционных материалов, являющихся структурно-неоднородными сре-
дами, базируются на макро- и микромеханическом подходах.
Слайд 51Механические свойства
Механические свойства материалов характеризуют возмож-
ность их использования в изделиях, эксплуатируемых
виях воздействия механических нагрузок. Основными показа-
телями таких свойств служат параметры прочности, твер-
дость и триботехнические характеристики. Они зависят не
только от природы материалов, но и от формы, размеров и
состояния поверхности образцов и условий эксплуатации об-
разцов.
Прочность – свойство материалов сопротивляться разруше-
нию, а также необратимому изменению формы образца под
воздействием внешних нагрузок. Прочность определяется си-
лами взаимодействия атомов, составляющих материал.
Слайд 52Критическому расстоянию α’ соответствует максимальная по
абсолютной величине сила притяжения F(γ). Если
жении образца внешняя сила, действующая на пару атомов,
превосходит F(γ), атомы будут удаляться друг от друга. Чтобы
разделить образец на части, такая сила должна действовать
на каждую пару атомов. Напряжение σТ ,отвечающее силе
F(γ), соответствует теоретической прочности. Если в твер-
дом материале на участке, размер которого соизмерим с меж-
атомным расстоянием, действует напряжение, большее σТ, то
на этом участке образуется трещина. Напряжения особенно
велики у краев трещин, где концентрация напряжений растет
с увеличением размера трещины. Рост трещины продолжает-
ся до тех пор, пока в результате слияния с другой трещиной
одна из трещин не распространится на все сечение образца,
что приведет к его разрушению.
Слайд 53Деформирование - изменение относительного расположения
частиц в материале. Наиболее простые его
ние, сжатие, изгиб, кручение, сдвиг. Деформация - изменение
формы и размеров образца в результате деформирования.
Параметры деформирования - относительное удлинение:
ε = (L – L0)/L0, (L и L0 - длина образца исходная и после де-
формирования, угол сдвига - изменение прямого угла между
лучами, исходящими из одной точки в образце, при его дефо-
рмировании. Для описания деформирования твердых тел
произвольной формы используют тензор деформации. Его
образуют шесть величин: относительные удлинения микро –
объема материала в направлениях осей прямоугольной сис –
темы координат и углы сдвига этих осей при деформировании
тела. Деформацию называют упругой, если она исчезает пос-
ле снятия нагрузки, или пластической, если не исчезает.
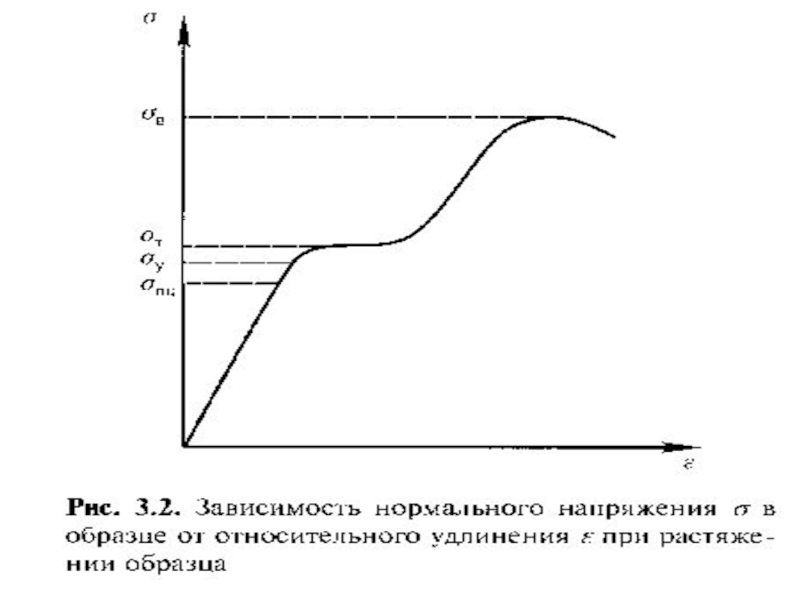
Слайд 55Из-за дефектов в материале экспериментальная прочность
значительно меньше теоретической, поскольку нагрузка
пределяется неравномерно по сечению образца. Материалы
характеризуются технической прочностью, основные характе-
ристики которой удобно рассмотреть с помощью выше приве-
денной диаграммы растяжения. Предел пропорциональности-
это характеристика, обозначаемая σПП , является верхней гра-
ницей области напряжений, где реализуется закон Гука.
Предел упругости - напряжение, при котором остаточные де-
формации достигают значения, установленного техническими
условиями (σУ ). Он ограничивает область упругой деформа –
ции. При простом растяжении (сжатии) σ = Е ε, где Е – модуль
Юнга или модуль продольной упругости, который характери-
зует сопротивление материалов упругой дефоормации (растя
жению, сжатию); ε – относительная деформация.
Слайд 56При сдвиге в материале по направлению сдвига и по нормали
к нему
G – модуль сдвига, характеризующий упругость материала
при изменении форму образца, объем которого остается пос-
тоянным; γ – угол сдвига. При всестороннем сжатии в мате –
риале по всем направлениям действует нормальное напря –
жение σ = КΔ, где К – модуль объемной упругости, который
характеризует сопротивление материала изменению объема
образца, не сопровождающемуся изменением формы; Δ –
относительное объемное сжатие.
Постоянной величиной, характеризующей упругость материа-
ла при одноосном растяжении, является коэффициент Пуас-
сона: ν = l ε´l/ ε, где ε´ - относительное поперечное сжатие, ε-
относительное продольное удлинение образца.
Слайд 57Для однородных изотропных тел модули упругости одинаковы
по всем направлениям и
G = Е/[2(1 + ν)], К = Е/[3(1 - 2 ν)].
Следовательно, упругие свойства изотропных материалов оп-
ределяются двумя независимыми постоянными «Е» и «ν».
Для большинства металлов ν = 0,3. Для несжимаемого мате-
риала ν = 0,5, поэтому G = Е/3 и К → ∞. У анизотропных ма –
териалов «Е», «G» и «ν» зависят от направления действия
нагрузки.
Предел текучести – напряжение, при котором в образце начи-
нает развиваться пластическая деформация. Она отвечает
нижнему положению площадки текучести на диаграмме σ =
= f (ε) для материалов, разрушению которых предшествует
заметная пластическая деформация (либо условный предел
текучести, определяемый ТУ).
Слайд 58Предел прочности – напряжение, соответствующее максима –
льному (в момент разрушения образца)
Отношение наибольшей силы, действующей на образец, к ис-
ходной площади его поперечного сечения называют услов-
ным пределом прочности, а также временным сопротивле-
нием, разрушающим напряжением. Истинный предел проч-
ности – отношение растягивающей силы непосредственно
перед разрывом к наименьшей площади поперечного сече-
ния образца в шейке.
Слайд 59Динамические характеристики
Динамическая прочность – сопротивление материала нагруз-
кам, значение, направление и
быстро изменяются во времени. При этом появляется запаз-
дывание текучести - явления, при котором при мгновенном
(очень быстром)приложении нагрузки, вызывающей текучесть
материала при статическом напряжении, пластическая дефор-
мация возникает не тотчас, а по истечении некоторого проме-
жутка времени – периода запаздывания текучести t. Если наг-
рузку снять до истечения этого периода, остаточная дефор-
мация не возникает, т.е. материал деформируется упруго.
Ударная вязкость измеряется работой разрушения надрезан-
ного образца при ударном изгибе и служит для оценки t.
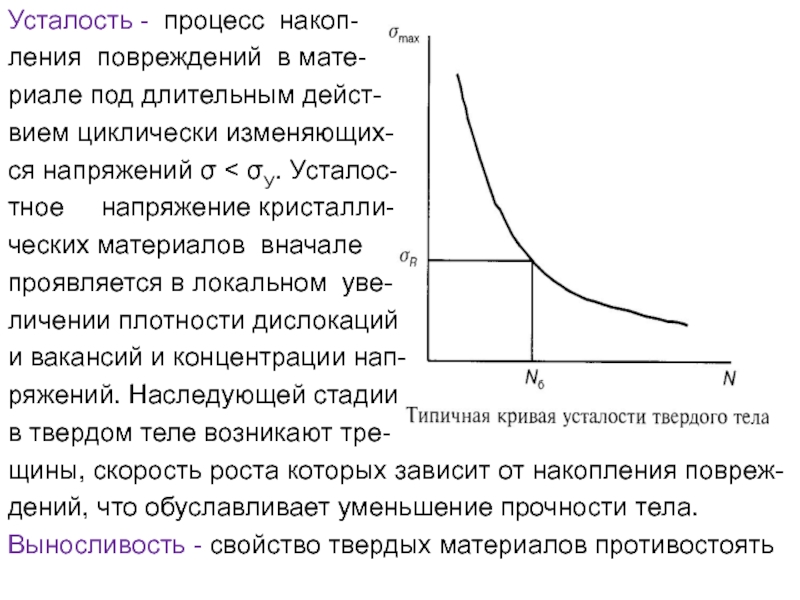
Слайд 60Усталость - процесс накоп-
ления повреждений в мате-
риале под длительным дейст-
вием циклически
ся напряжений σ < σУ. Усталос-
тное напряжение кристалли-
ческих материалов вначале
проявляется в локальном уве-
личении плотности дислокаций
и вакансий и концентрации нап-
ряжений. Наследующей стадии
в твердом теле возникают тре-
щины, скорость роста которых зависит от накопления повреж-
дений, что обуславливает уменьшение прочности тела.
Выносливость - свойство твердых материалов противостоять
Слайд 61усталости. Усталостный процесс характеризуется зависимос-
тью между накопленным в образце повреждением и
циклов нагружения, график которой называют кривой устало-
сти. Цикл нагружения – совокупность переменных значений
напряжений и деформаций, происходящих за один период их
изменения, повторяющийся в процессе длительного нагруже-
ния образца. Предел выносливости – наибольшая величина
напряжения σR, которая не приводит к разрушению образца
при базе испытаний N(б).
На выносливость образца влияют концентрация повреждений
на поверхности образца, температура и физико – химическая
активность среды.
Усталостные повреждения зарождаются в местах нарушения
регулярности структуры материала, из которого изготовлен
образец. Характеристики усталости подчиняются теории ве –
роятности как и нерегулярности структуры.
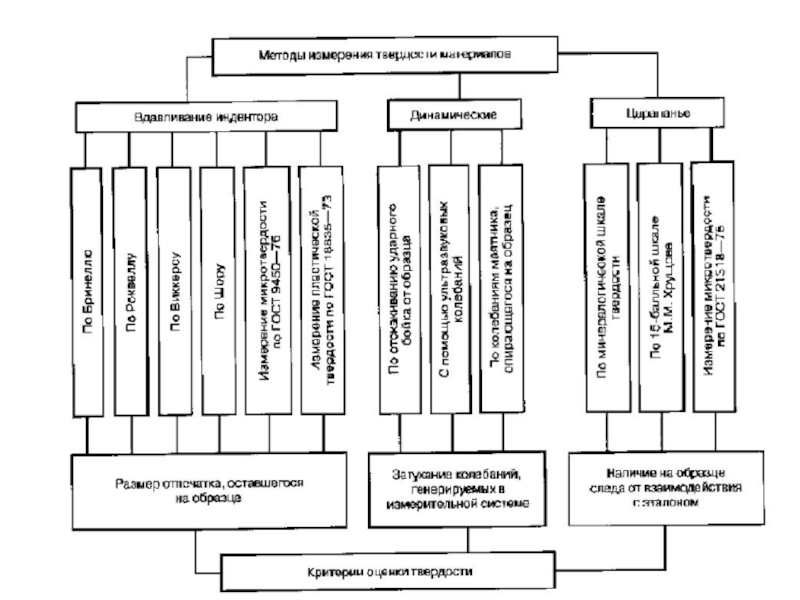
Слайд 62Твердость является механической характеристикой материа-
лов, комплексно отражающей их прочность, пластичность, а
также свойства поверхностного слоя образцов. Она выража –
ется сопротивлением материала местному пластическому де-
формированию, возникающему при внедрении в образец бо-
лее твердого тела – индентора. В зависимости от способа
внендрения и свойств индентора твердость материалов оце –
нивают по различным критериям, в соответствии с одним из
трех методов: а) вдавливание индентора, б) динамические
инденторы, в) царапание. Существует несколько ГОСТов оп-
ределения твердости материалов (см. ниже диаграмму).
Слайд 64Триботехнические характеристики содержат информацию об
эффективности применения материалов в узлах трения. Про-
блемы
ностроении.
Внешнее трение - сопротивление относительному перемеще-
нию двух соприкасающихся тел, находящихся в одной или в
разных фазах, в плоскости их касания, которое сопрвождает-
ся рассеянием энергии.
Изнашивание - процесс разрушения и отделения материала с
поверхности твердого тела и (или) накопления его остаточной
деформации при трении, проявляющейся в изменении разме-
ров и (или) формы тела. Износ - результат изнашивания.
Смазывание - действие смазочного материала, в результате
которого уменьшается сила трения и (или) интенсивность
изнашивания.
Слайд 65Основные триботехнические характеристики твердых матери-
алов - износостойкость, прирабатываемость и коэффициент
трения.
Износостойкость
ление изнашиванию в определенных условиях трения. Вели –
чину износа выражают в единицах длины, объема или массы.
Отношение величины износа «u» к интервалу времени «t», в
течение которого он возник, или к пути «L», на котором проис-
ходило изнашивание, представляют собой соответственно
скорость изнашивания ν = u/t и интенсивность изнашива –
ния I = u/L. Износостойкость материалов оценивают величи –
ной, обратной скорости и интенсивности изнашивания. Выде-
ляют три стадии изнашивания: I – начальное изнашивание,
Наблюдаемое при приработке деталей узлов трения, которое
сопровождается изменением геометрии поверхности трения,
Слайд 66структуры поверхностных слоев материала и протекает с за-
медляющейся скоростью; II –
изнашивание, для которого характерна небольшая и постоян-
ная скорость изнашивания, III – резкое возрастание скорости
изнашивания (катастрофическое изнашивание).
Прирабатываемость – свойство твердого материала умень-
шать силу трения, температуру и интенсивность изнашивания
в процессе приработки, т.е. начальный период трения пары.
Обеспечение износостойкости связано с предупреждением
катастрофического изнашивания. Существует классификация
видов изнашивания (абразивное, адгезионное, усталостное и
прочие). Основная причина всех видов изнашивания – работа
сил трения. Как правило, предсказать триботехнические ха –
рактеристики материалов, зная другие параметры механичес-
ких свойств (напр., деформационно-прчностные) нельзя.
Слайд 67Напряжения и деформации
При нагружении в металлах и сплавах возникают механичес-
кие напряжения,
ное состояние. Равновесное состояние материала может
стать неравновесным вследствие неравномерного нагрева-
ния, неоднородных структурных превращений в материале
или под воздействием физических полей. В зависимости от
масштаба элементов структуры материала, на которых лока-
лизованы напряжения, последние разделяют на три катего-
рии: микронапряжения 1-го рода, уравновешенные в объеме
всего образца; 2-го рода, уравновешенные в объеме кристал-
литов (зерен) или их частей и 3-го рода, локализованные в
объеме кристаллической ячейки при нарушении ее порядка.
Слайд 68С возрастанием механических нагрузок напряженно-дефор -
мированное состояние металлического материала изменяет-
ся следующим
ция, затем она превращается в пластическую и, наконец, при
превышении определенного порога напряжений наступает
разрушение материала.
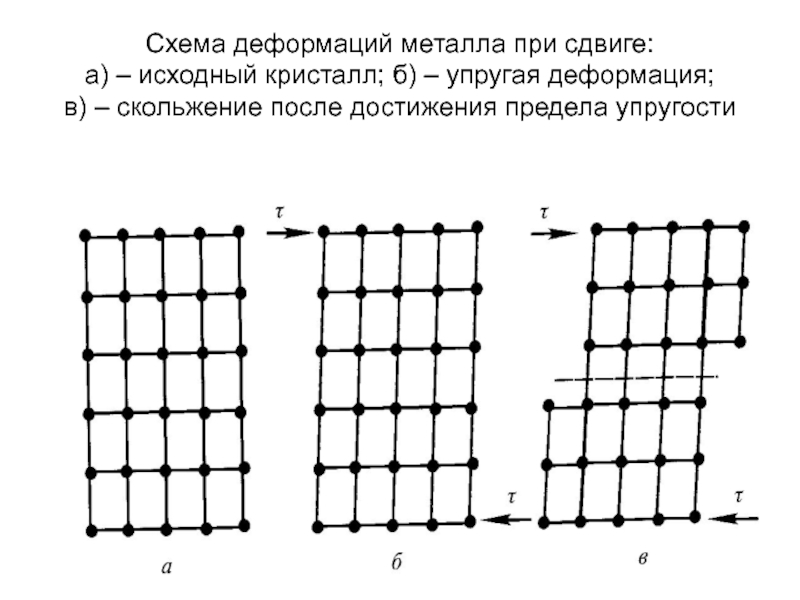
Механизм упругой деформации металлов состоит в незначи –
тельном и полностью обратимом смещении атомов, которое
нарушает баланс сил их взаимодействия в кристаллической
решетке.
Пластичческая деформация монокристаллов металла связа-
на с необратимыми смещениями атомов в его кристалличес –
кой решетке, в результате которого части кристалла сдвига –
ются относительно друг друга (скольжение) или перестраива-
ются в кристаллическую структуру, зеркально симметричную
относительно неискаженной части.
Слайд 69Схема деформаций металла при сдвиге: а) – исходный кристалл; б) – упругая
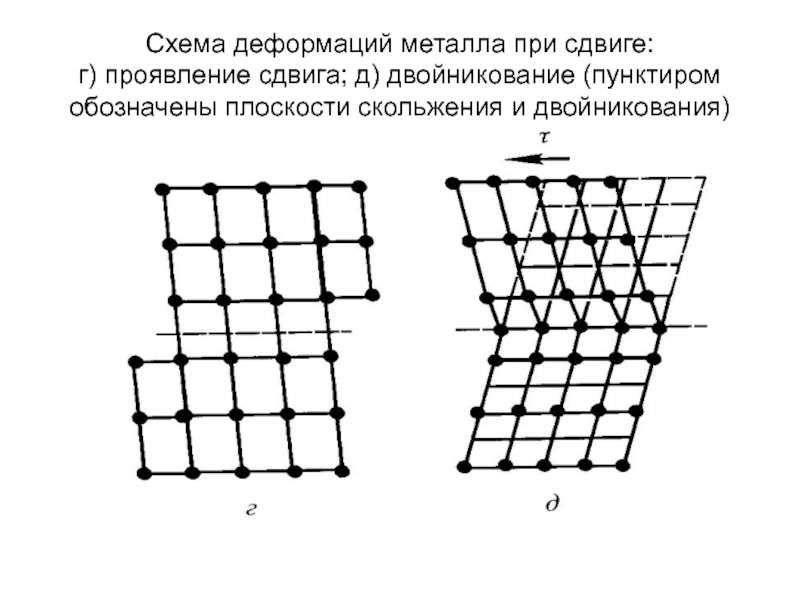
Слайд 70Схема деформаций металла при сдвиге: г) проявление сдвига; д) двойникование (пунктиром обозначены
Слайд 71В идеальном кристалле, не имеющем дефектов структуры, для
сдвига атомного слоя на
ются очень большие касательные напряжения, вызывающие
одновременный разрыв связей у всех пар атомов в плоскости
скольжения. Это критическое напряжение соответствует теоре-
тической прочности кристалла:
τ(к) = σ/2π = 0,16σ,
где σ – модуль упругости при сдвиге.
В технических металлах для сдвига кристаллов на одно меж-
атомное расстояние требуется напряжение в ~ 1000 раз мень-
шее, что объясняется наличием дефектов структуры.
Слайд 72Термическая обработка
Термическую обработку мы разберем на примере стали – ши-
роко широко
боткой называют процесс , состоящий из операций нагрева-
ния изделий и заготовок до определенной температуры, вы –
держке при этой температуре и охлаждении с заданной ско –
ростью. Термическая обработка позволяет изменять в жела-
тельном направлении структуру и свойства металлического
материала, причем диапазон изменений может быть очень
широким. Термическую обработку часто сочетают с химичес –
ким воздействием или пластической деформацией металла,
что расширяет возможности термической обработки. Т.о. ос-
нована на протекании процессов перекристаллизации.
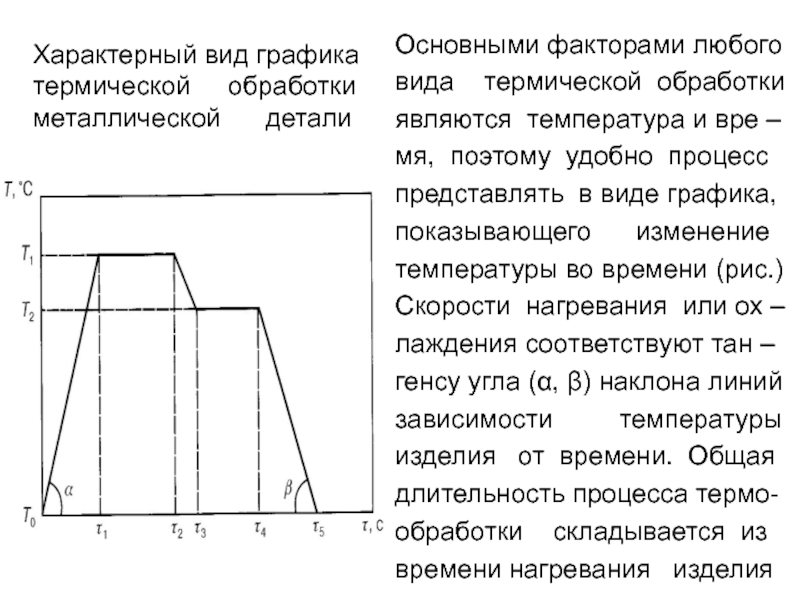
Слайд 73Характерный вид графика
термической обработки
металлической детали
Основными факторами любого
вида
являются температура и вре –
мя, поэтому удобно процесс
представлять в виде графика,
показывающего изменение
температуры во времени (рис.)
Скорости нагревания или ох –
лаждения соответствуют тан –
генсу угла (α, β) наклона линий
зависимости температуры
изделия от времени. Общая
длительность процесса термо-
обработки складывается из
времени нагревания изделия
Слайд 74от исходной температуры Т(0) до заданной температуры Т(1),
времени выдержки при этой
ния до заданной температуры Т(2). Далее деталь выдержива-
ют при температуре Т(2) и охлаждают до температуры Т(0). В
результате термической обработки в металлах и сплавах про-
исходят структурные изменения, обуславливающие равновес-
ное (стабильное) или неравновесное (метастабильное) сос-
тояния их структуры. Существуют чисто термическая обработ-
ка и ее сочетание с пластической деформацией и химическим
воздействием. Наибольшее распространение получили сле –
дующие виды термической обработки.
Отжиг 1-го рода- нагревание, выдержка, охлаждение изделия
с целью снятия остаточных напряжений и искажений кристал-
лической решетки.
Отжиг 2-го рода- нагревание выше температуры фазового
Слайд 75превращения и медленное охлаждение, приводящее сплав в
равновесное состояние.
Закалка- нагревание до
пература фазового превращения, выдержка при этой темпера
туре и быстрое охлаждение, после которого фиксируется сос-
тояние сплава, соответствующее температуре фазового прев-
ращения.
Отпуск- нагревание закаленного изделия до температуры ни-
же критической температуры фазового превращения и охлаж-
дение. Это приводит к снятию остаточных напряжений после
закалки. Отпуск, проводимый при комнатной температуре или
несколько ее превышающей, называют старением.
Слайд 76Наноматериалы
Наноструктурные материалы, или наноматериалы, содер-
жат структурные элементы (кристаллы, волокна, слои, поры)
размер
одном направлении. Благодаря уникальным свойствам нано-
материалов проблемы их создания стали предметом актуаль-
ного и перспективного направления современного материало-
ведения. Наноматериалы получают нетрадиционными мето-
дами, совокупность которых получило название нанотехноло-
гия.
История наноматериаловедения началась с идей американс-
кого физика Р.Фейнмана, который предложил «конструиро-
вать материалы методами молекулярной архитектуры (1959 г)
Слайд 77В 1969 г. советский физикохимик П.А.Рибиндер выдвинул кон-
цепцию упрочнения материалов посредством
структурных компонентов. Термин «нанотехнология» впервые
был использован в 1974 г. японцем Танигуче при обсуждении
проблем обработки хрупких материалов. Американский мате-
риаловед Глейтер ввел (1981) понятие «нанокристаллические
материалы» и предложил метод их получения путем испаре-
ния – конденсации металлов, вакуумной консолидации in situ
(месте нахождения) ультрадисперсных частиц и формирова-
нии из них материалов при высоких давлениях.В это же время
при производстве транзисторов были впервые использованы
тонкие пленки толщиной порядка 10 нм. Событием стало соз-
дание на этой основе так называемого полевого транзистора-
униполярного транзистора, в котором изменение тока проис-
ходит под действием перпендикулярного ему электрического
поля, создаваемого входным сигналом.
Слайд 78В 1981 г. был создан сканирующий туннельный микроскоп, с
помощью которого стало
нометровом масштабе.
Интерес к наноматериалам вызван следующим:
методы нанотехнологии позволяют получить принципиально
Новые материалы с характеристиками, значительно превос-
ходящими сегодняшний уровень лучших материалов;
нанотехнология объединила усилия специалистов в области
физики, химии, материаловедения, биологии, медицины, ком-
пьютерной техники, экономики, социологии и пр., что не могло
не привести к замечательным результатам;
решение проблем нанотехнологии выявило много пробелов в
теоретическом и прикладном материаловедении.
Во многих странах, в том числе и в России, приняты государс-
твенные программы, предусматривающие развитие наномате
риаловедения и нанотехнологии..
Слайд 79В настоящее время считают приоритетными направлению:
Молекулярный дизайн материалов с заданными свойствами;
Нанопроцессоры
и логические операции, заданные программой преобразова-
ния информации) с низким уровнем энергопотребления;
Нанопроцессоры с рекордной производительностью;
Миниатюрные запоминающие устройства с огромным объе-
мом памяти;
Новые лекарственные препараты, применяемые в сверхма-
лых дозах и методы их адресной доставки к определенным
органам;
Новые методы мониторинга (оперативного контроля) окружа-
ющей среды и организма человека с ромощью наносенсоров
(чувствительных элементов).
Оборот мирового рынка наноматериалов в 2002 достиг $300
млрд, через 10 лет - $1 трлн.
Слайд 80Классификация наноматериалов
Консолидированные наноматериалы - конструкционные мате-
риалы, разновидности фольги и покрытия из
сплавов, состоящие из наночастиц, прочность связи между
которыми достаточно высока. Конструкционные материалы
получают методами порошковой металлургии, разновидности
фольги – интенсивным пластическим деформированием тон –
кого слоя наночастиц, покрытия – конденсацией металлов из
газовой фазы. Полупроводниковые наноматериалы использу-
ют в консолидированном виде и в виде отдельных наночас-
тиц, вхоодящих в состав коллоидных систем.
Фуллерены - новая (обнаружена в 1980 –е гг.) аллотропная
форма углерода, имеющая шарообразые молекулы С(60) или
Слайд 81С(70). Их поверхность состоит из 5- и 6-угольников, образован
ных атомами С.
Название фуллеренам дано по имени американского архитек-
тора Р.Б.Фллерона, разработавшего конструкцию куполооб-
разной крыши («геодезический купол»), составленный из 5-
и 6-угольников, наподобие футбольного мяча. В 1991 г. япо –
нец С.Ишима обнаружил углеродные нанотрубки - тубулены в
продуктах электродугового испарения графита.
Нанопористые материалы различной природы характеризуют-
ся наличием в их структуре пор размером менее 100 нм. Их
основное назначение – системы фильтрования, а именно
мембранные фильтроэлементы.
Катализаторы, используемые при гетерогенном (контактном)
катализе, тем более активны, чем больше их удельная повер-
хность – это нанодисперсные частицы активного вещества,
закрепленные на пористых носителях.
Слайд 82Супрамолекулярные структуры в большей мере (лат. supra –
над, выше) –
называемого нековалентного синтеза полимеров с образова –
нием слабых (ван-дер-ваальсовых, водородных и др.) связей
между молекулами и их ансамблями. Чаще всего их модифи-
цируют ионами металлов, придавая фотохимическую, элект-
рохимическую активность и другие свойства.
Дендримеры - (от греческого dendr – дерево) высокомолеку –
лярные структуры, состоящие из центральной молекулы, от
которой растут и разветвляются макромолекулярные ветви.
Дендримеры имеют нанометровые размеры, в их структуре
есть полости («молекулярные контейнеры»), в которые можно
помещать наночастицы, например, лекарственных веществ.
Таким образом, удается адресно доставлять лекарства к
заданным органам человека.
Слайд 83Свойства наноматериалов
Свойства наноматериалов в большой мере определяются
размерными эффектами
когда размеры наночастицы соизмеримы с одной из характер-
ных длин – длиной свободного пробега носителей заряда,
длиной волны де Бойля, диффузной длиной и т.д. Именно
размерные эффекты обуславливают немонотонность зависи-
мостей свойство – размер наночастицы. Существенное влия-
ние на эти зависимости оказывает распределение в наночас-
тице дефектов, примесей, нанопор и механических напряже-
ний. Механизмы проявления размерных эффектов внутри н
ночастицы и на поверхностях раздела наноматериала, состо-
ящего из этих частиц, различны.
Слайд 84Переход от крупнокристаллических к наноструктурным полу –
проводникам сопровождается увеличением ширины запре
щенной зоны. С уменьшением размера частицы увеличивает-
ся доля составляющих ее атомов, которые расположены в ее
поверхностном слое. Это также обуславливает изменение
электрических свойств наноматериалов, а также влияет на их
оптические и магнитные свойства. Наличие большого количе-
ства атомов на поверхности раздела оказывает большое вли-
яние на температурные характеристики наноматериалов.
Экспериментально установлено повышение теплоемкости,
понижение температуры плавления наноматериалов на осно-
ве металлов и керамики, а также температуры стеклования
полимерных наноматериалов по сравнению с анологичными
макроматериалами.Следовательно,переход к наноструктурам
позволяет регулировать физические свойства материалов.
Слайд 85Границы раздела между частицами являются препятствиями
на пути распространия дислокаций и трещин,
вает повышение твердости в 5 … 6 раз для металлических и
в 2 … 3 раза для керамических наноматериалов. Наноматери-
алы в большинстве случаев термодинамически неравновесны
из-за обилия поверхностей раздела, наличия нестабильных
фаз, микропор и механических напряжений. Это эволюциони-
рует наноструктуры и приводит к изменению их свойств. Ста-
билизация наноструктур является актуальной проблемой на-
номатериаловедения.
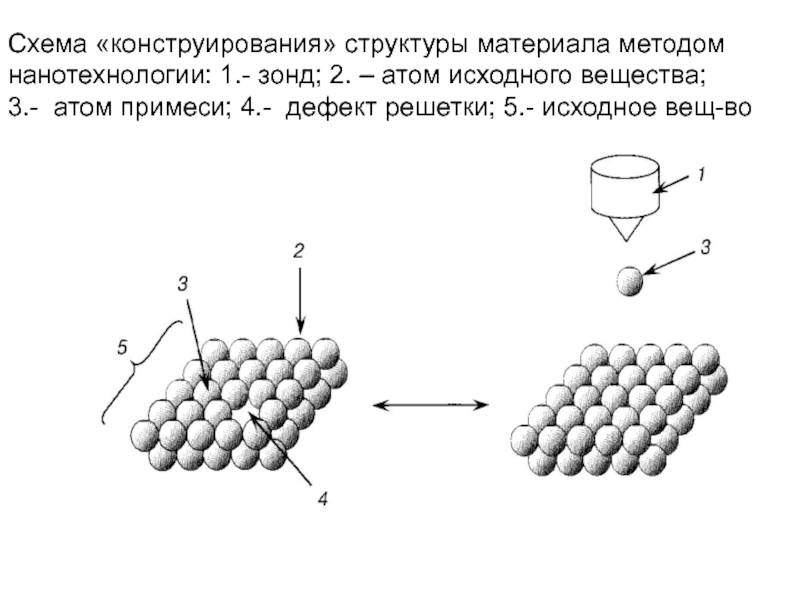
Методы нанотехнологии в классическом варианте предполо –
гают «конструирование» материала с заданными свойствами
путем манипуляций с отдельными атомами или молекулами.
Схема такого процесса показана ниже. С помощью зонда уда-
ляют из исходного ансамбля частиц атом примеси и «вставля-
ют в вакантные места решетки атомы нужного элемента
Слайд 86Схема «конструирования» структуры материала методом нанотехнологии: 1.- зонд; 2. – атом
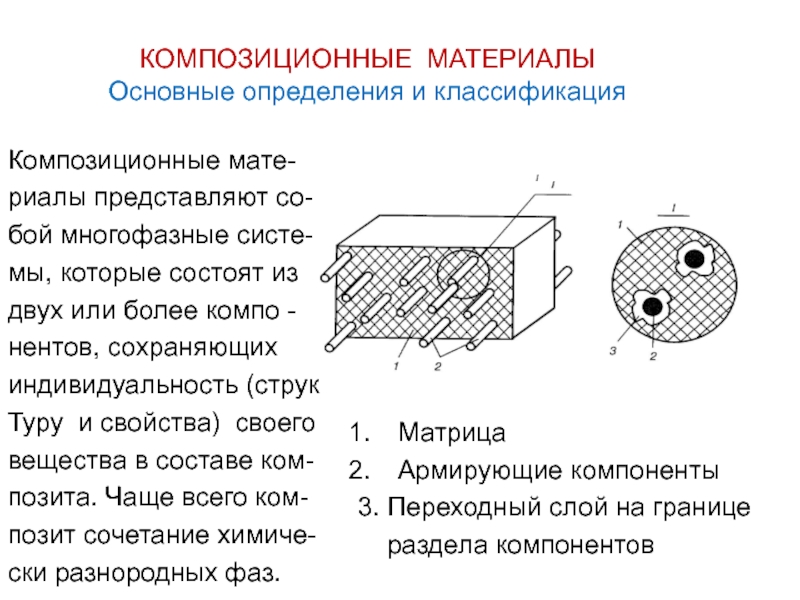
Слайд 87КОМПОЗИЦИОННЫЕ МАТЕРИАЛЫ
Основные определения и классификация
Композиционные мате-
риалы представляют со-
бой многофазные систе-
мы, которые
двух или более компо -
нентов, сохраняющих
индивидуальность (струк
Туру и свойства) своего
вещества в составе ком-
позита. Чаще всего ком-
позит сочетание химиче-
ски разнородных фаз.
Матрица
Армирующие компоненты
3. Переходный слой на границе
раздела компонентов
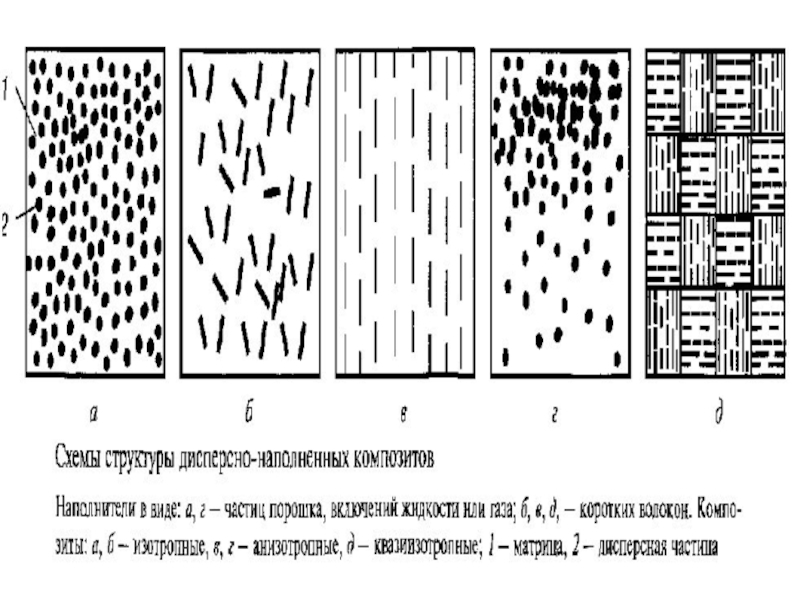
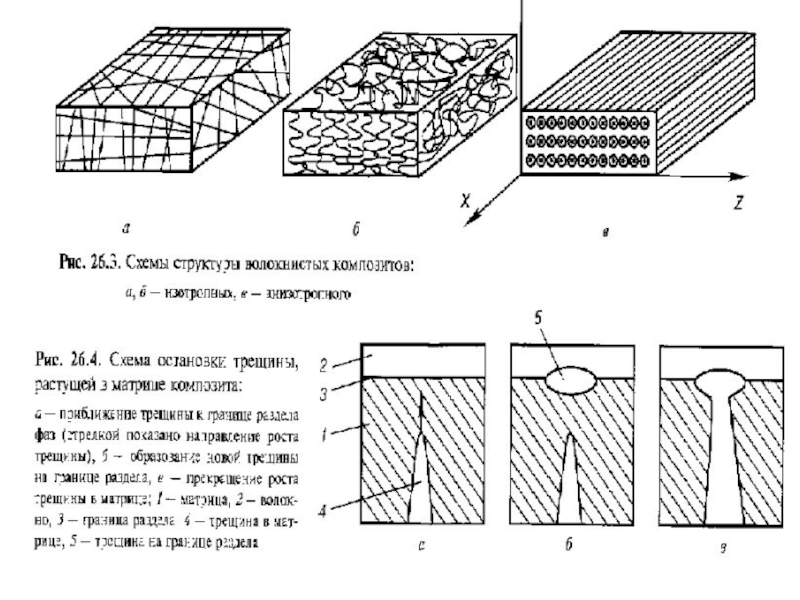
Слайд 88Размер фазовых включений в композите обычно превышает
разрешающую способность
мкм). Переходные поверхностные слои (на рис. обозначены 3)
расположены на границах раздела матрицы и наполнителей.
Свойства вещества переходного слоя (иногда его называют
третьей фазой) отличаются от свойств вещества основных
фаз. К идее о целесообразности 3-го фазы как средстве улуч-
шения взаимодействия несовместимых веществ пришел еще
Платон (428 – 348 гг до нашей эры). Древнегреческий философ
разрабатывал эту идею для объяснения того, как Вселенная
может быть построена из несовместимых земли, воды, огня и
воздуха. Свойства переходного слоя, прежде всего прочность
сцепления (адгезия) с компонентами, в большей мере опреде-
ляют эксплуатационные характеристики композита и их ста –
бильность во времени. При нагружении напряжения достигают
наибольших значений на границах раздела компонентов.
Слайд 89Главная функция переходного слоя состоит в том, чтобы сни -
зить локальные
дачу нагрузки на границе раздела. Поэтому переходный слой
не должен разрушаться под действием усадочных напряже -
ний, которые появляются при отверждении матрицы, а также
термических напряжений, возникающих при эксплуатации ком-
позита из-за разницы в температурных коэффициентах линей-
ного расширения матрицы и наполнителей.
В материаловедении используют термин аддитивность, кото-
рый означает, что величина какого-либо параметра сложного
объекта равна сумме значений этого параметра, соответству-
ющих его частям. Применяя этот термин, можно утверждать,
что свойства композита не аддитивны свойствам его компоне-
тов. Композиты разрабатывают потому, что им присущ
синергизм.
.
Слайд 90Синергизм (в медицине) - объединенное действие двух лекар-
ственных препаратов, которое является более
сумма действий этих двух лекарств
Т.о., значение каждого из основных параметров композита
превышает сумму соответствующих значений всех его компо-
нентов.
Композиты встречаются природные и искуственные и синте-
тические.
По назначению композиты разделяют на общетехнические и
специального назначения. Первые предназначены для восп –
приятия и передачи механической нагрузки. Вторые выполня-
ют в составе изделий специальные функции: снижают трение
и изнашивание, звуко- и теплоизоляция и т.п.
По материалу матрицы различают:
а) Полимерные композиты (термопластичные, на основе
смесей полимеров);
Слайд 91б) Металлические композиты (в том числе получаемые мето
дом порошковой металлургии и
неоднородных фаз);
в) Керамические и другие неорганические композиты (на ос-
нове неорганических полимеров, на минеральной, углеродной
оксидной и других неорганических матрицах);
г) Комбинированные (полиматричные) композиты.
По природе компонентов, вводимых в матрицу, композиты раз-
деляют на наполненные и армированные.
Наполненные композиты содержат в матрице наполнители –
дисперсные частицы неорганических или органических ве –
ществ, которые могут находиться в любой фазе. Наполнители
выполняют в композитах следующие функции: 1) изменяют ме-
ханические показатели композитов и придают им специальные
свойства (электрические, химические, звукопоглощающие и пр
Слайд 922) улучшают технологичность композитов, т.е. их приспособ-
ленность к переработке в изделия
ные компоненты улучшают прессуемость порошковых смесей,
активные добавки усиливают адгезию компонентов т.п.);
3) снижают стоимость изделий, т.к. наполнители, как правило,
дешевле связующих.
Армированные композиты имеют в составе арматуру (армиру-
ющие элементы) более прочную, чем матрица. С помощью
наполнителей прочность изделий можно увеличить в 1,5 … 2
раза, а путем армирования – на порядок и более. Вклад арми-
рующих элементов в свойства композитов нередко является
определяющим. Поэтому в названиях композитов часто нахо-
дит отражение химическая природа арматуры – графитоплас-
ты, металлокерамика, стекловолокниты и т.п. В состав компо-
зитов могут входить и наполнители, и армирующие элементы.
Слайд 93По размеру фазовых включений разработчики материалов из-
Начально отличали композиты от
материалов. Типичным признаком композита являлись разли-
чимые в его структуре невооруженным глазом разнородные
включения. По мере совершенствования технологии получе-
ния материалов компоненты становились все более мелкими
и различать их приходилось с помощью микроскопа (~ 1 мкм).
В настоящее время возникла тенденция формирования ком –
позиционных материалов из частиц нанометрового размера.
Благодаря значительному поверхностному слою свойства на-
ночастицы значительно отличаются от свойств материала ее
составляющего. Высокая прочность композитов, высокая уда-
рная вязкость обусловлены тем, что сила удара поглащается
миллионами наночастиц, что приводит к диссипации (рассеи-
ванию) энергии во множестве микротрещин, которые не нару-
шают целостность композита.
Слайд 96Теплоемкость. Общие сведения.
Под теплоемкостью тела, С, понимают количество теплоты
зи данной температуры. Теплоемкость – величина скалярная.
Часто для анализа пользуются понятием удельной теплоем-
кости (расчет ведется на 1 кг) или молярной теплоемкостью
(расчет на 1 моль). Ниже мы чаще всего будем иметь дело с
молярной теплоемкостью. Из определением молярной тепло-
емкости можно записать:
СР = δQ/(m/µ)dT = δA/(m/µ)dT + dU/(m/µ)dT = pdV/(m/µ)dT + dU/(m/µ)dT, (1.1)
Слайд 97Где СР – молярная теплоемкость при постоянном давлении, δQ – теплота,
Слайд 98Электронная теплоемкость при гелиевых температурах может
значительно превышать теплоемкость кристаллической ре
решетки. Однако при более высоких температурах электрон -
ная теплоемкость составляет лишь малую долю решеточной
теплоемкости. Экспериментально обычно определяют тепло-
емкость при постоянном давлении, СР, которая превышает
теплоемкость при постоянном объеме, СV, за счет работы,
производимой при расширении против внутреннего давления
Для идеального газа разность СР – CV = R (R – газовая посто-
янная). Поскольку коэффициенты расширения конденсиро –
ванных сред меньше, чем газовых систем, то и разность СР –
CV для твердых тел (в том числе и металлов) будет меньше.
Она находится с помощью измерений сжимаемости, опреде –
ния температур плавления и т.д.
Слайд 99
Анализ имеющегося в литературе большого количества экс -периментальных данных
В частности, теплоемкость твердых тел составляет при ком -натной температуре ~ 25 Дж/моль К (закон Дюлонга – Пти). С повышением температуры теплоемкости зачастую незначи -тельно увеличивается (прежде всего за счет роста электрон -ной теплоемкости). С понижением температуры теплоемкость уменьшается, стремясь к нулю при Т → 0 К. Правило Неймана – Коппа указывает на то, что во многих случаях теплоемкость соединений складывается аддитивно из теплоемкостей их компонентов. Объяснение уменьшения теплоемкости с пони -жением температуры нельзя объяснить в рамках классичес -кой статистической механики. Напротив, классическая статис -тика обосновывает закон Дюлонга – Пти. Согласно этой тео -рии, внутренняя энергия одного моля U = 3RT, а СV, соответст- венно, равна dU/dT = 3R ≈ 25 Дж/мольК.
Слайд 100Уменьшение теплоемкости при понижении температуры –
чисто квантовый
в 1907 г. Он предположил, что средняя энергия линейного
гармонического осциллятора равна не kТ (k – постоянная
Больцмана), а как это предложил в 1900 г. М.Планк:
< Е > = ħω/(exp(ħω/kT) – 1),
где ω – собственная частота осциллятора. Такой подход поз-
волил рассчитать вклад в теплоемкость за счет колебаний
осциллятора, Сω:
Сω = R(Ө/Т)2exp(Ө/Т)/( exp(N) – 1)2 ,
где Ө = ħω/T получило название характеристической темпе –
ратуры Эйнштейна. Эта модель получила хорошую экспери –
ментальную проверку для газовых систем. Однако для крис -
таллических конденсированных структур модель не дает
хорошего согласия с опытом.
Слайд 101Дебай в 1912 г. установил необходимость учета связей атомов в кристалле.
Для низких температур: CV РЕШ= 233,8R(Т/ ӨD)3.
Для высоких температур CV РЕШ= 3R – (3/20)R(ӨD/T)2.
Где ӨD = ħωO/T носит название характеристической темпера- туры Дебая (функции Дебая).
Слайд 102
Опыт показывает, что с помощью этой функции можно в боль- шинстве
CV РЕШ = βТ3.
Слайд 103Свободные электроны в металле
Природа носителей тока в металлах долгое время была
вестна. Для выяснения этого вопроса были предприняты спе-
циальные опыты.
Рикке, пропуская длительное время ток через составной про-
водник (медь – алюминий), установил, что носители тока сво-
бодные частицы, не связанные с атомами вещества и одина-
ковые для всех металлов. Друде и Лоренц предположили, что
это свободные электроны, а Мандельштамм и Папалекси
(Россия, 1913 г.) и Толмэн и Стюарт (США, 1916) эксперимен-
тально (методом регистрации разности потенциалов с концов
резко заторможенного проводника) показали это.
Как отмечалось выше, при образовании кристаллической
Слайд 104Как отмечалось выше, при образовании кристаллической ре –
шетки валентные электроны легко
мов и становятся свободными. Атомы, «потерявшие» элект-
роны, превращаются в положительно заряженные ионы. Мож-
Но оценить концентрацию свободных электронов :
n = (D/A)NA,
где D – плотность металла, А – масса килоатома, NA – число
Авогадро.
По порядку величины концентрация свободных электронов
составляет (1028 – 1029) 1/м3 .
В основе классической электронной теории лежит модель
идеального электронного газа.
Предполагается, что электроны не взаимодействуют на расс-
тоянии ни друг с другом, ни с ионами решетки.
Слайд 105В отсутствие электрического поля в проводнике свободные
электроны двигаются хаотично, случайно
ми решетки. В результате столкновений между решеткой и
электронным газом устанавливается тепловое равновесие.
Скорость хаотического движения можно оценить из уравнения
(mv2/2) = (3/2)kT и v ≈ 105 м/с.
При наличии электрического поля на хаотическое движение
накладывается упорядоченное движение (дрейф) в направ -
лении, противоположном направлению поля.
Вектор плотности тока j, концентрация n, средняя дрей -
вовая скорость и заряд электрона е связаны между
собой: j = nе.
По порядку величины ~ 0,5·10-3 м/с,
Слайд 106Закон Ома в классической электронной теории
Непосредственной причиной электрического сопротивления,
по представлениям классической
ханические столкновения свободных электронов с ионами
кристаллической решетки.
Друде полагал, что при каждом столкновении электрон пол –
ностью теряет свою скорость направленного движения (абсо–
лютно неупругий удар), на некоторое время «захватывается»
ионом (иначе он не сможет отдать всю энергию за один удар
его масса много меньше массы иона). В промежутках между
столкновениями электрон движется равноускоренно со сред –
ней «дрейвовой» скоростью = umax/2 = a<τ> , где a – ускор-
ение электрона, <τ> - среднее время свободного пробега.
Слайд 107По второму закону Ньютона а = F/m = Ee/m где Е
ность поля в проводнике, e и m – заряд и масса электрона.
<τ> = <λ>/( +
т.к.
бодного пробега электрона,
го движения электрона. Тогда = e<λ>E/2m
j = nе, можно записать: j = (ne2<λ>/2m
(ne2<λ>/2m
Величина 1/σ = R - электросопротивление металла.
При соударении электрона с узлом кристаллической решетки
электрон передает часть энергии, связанной с направленным
движением решетки, в результате чего металл нагревается
(джоулево тепло). Можно показать, что тепловая энергия, вы-
деляющаяся в единице объема металла в единицу времени
численно равна w = σE2.
Слайд 108В рамках классической электронной теории доказывается, что
теплопроводность металла также, как и
обусловлена свободными электронами (закон Видемана –
Франца).
Слайд 109Затруднения классической теории металлов
Классическая электронная теория не в состоянии объяснить
ряд
1.Опыт показывает, что электросопротивление в широком ин–
тервале температур пропорционален температуре в первой
степени. Согласно теории, R ~ (Т)1/2 .
2. Согласно теории, теплоемкость кристаллической решетки
равно 3R (R – газовая постоянная). У металла, кроме того,
есть свободные электроны – их теплоемкость равна (3/2)R,
т.е. теплоемкость металлов должна быть в 1,5 раза больше,
чем диэлектрика. На практике они практически одинаковы.
3. Чтобы согасовать теоретические и экспериментальные зна-
чения R, нужны комбинации с <λ>.
4. Сверхпроводимость не объясняется никак.
Слайд 110ЭЛЕМЕНТЫ КВАНТОВОЙ ТЕОРИИ ТВЕРДЫХ ТЕЛ
Основные положения теории
Идея о двойственной, корпускулярно
электронов. Согласно классическим представлениям – элект-
рон – частица с резко очерченными границами. По квантовым
представлениям – электрон обладает не только свойствами,
присущими микроскопическим телам, - корпускулярными
свойствами, но и свойствами, присущими волнам - волновыми
свойствами.
2. Идея о дискретности значений энергии электронов. Класси-
ческая электронная теория металлов постулирует, что энер –
гия свободных электронов в металле (полная или кинетичес –
кая) является функцией теплового состояния системы, может
меняться непрерывно, принимая какие угодно значения.
Слайд 111Квантовая теория утверждает, что энергия свободных элект-
ронов в металле может принимать
торые, дискретные значения, изменения ее происходят пор –
циями – квантами.
3. Идея о неразличимости электронов в металле. По класси-
ческой статистике Максвелла – Больцмана частицы, образую-
щие макроскопическую систему, обладают индивидуальнос –
тью, могут быть пронумерованы. Квантовая теория полагает,
что частицы неразличимы и подчиняются не классической
статистике Максвелла – Больцмана, а квантовой статистике
Ферми – Дирака.
4.Принцип Паули. По квантовой теории состояние электрона и
в атоме и в кристалле определяется набором четырех кванто-
вых чисел. Согласно принципу в атоме, в кристалле не может
быть даже двух электронов с одинаковыми набором чисел.
Слайд 112Квантование энергии свободных электронов в металле
Полная энергия любого свободного электрона в
сумма потенциальной и кинетической энергий. Металл
Представляет для свободных электронов своеобразную потен
циальную яму, поскольку на электрон, покинувший металл,
действуют силы зеркального отображения и двойного элект-
рического слоя. Поскольку силы, действующие на любой сво-
бодный электрон, покидающие металл одинаковы, то и потен-
циальная энергия всех свободных электронов в металле оди-
накова. По знаку она отрицательна. Ход потенциальной энер-
гии в металле и за его пределами представлен на следующем
рисунке.
Слайд 114При образовании из отдельных атомов кристаллического тела
атомы сближаются на столь малые
ронные оболочки перекрываются, между атомами начинается
взаимодействие. Это взаимодействие приводит к тому, что
соответствующие энергетические уровни отдельных атомов
смещаются относительно друг друга – в результате вместо
одного одинакового для всех атомов уровня возникает N (N -
число атомов,объединившихся в кристалл) весьма близких,но
не совпадающих уровней. Образуется полоса или зона разре-
шенных энергетических уровней. Ширина образовавшейся по-
лосы может достигать нескольких электрон – вольт. Расстояние между соседними уровнями в зонах очень мало
порядка 10-22 – 10-23 эВ. В любом твердом теле зоны разре-
шенных значений энергии разделены зонами запрещенных
энергии.
Слайд 116Заполнение разрешенных энергетических уровне происходит
в соответствии с принципом Паули.
Особую роль
на, образовавшаяся в результате расщепления самого верх-
него занятого электронами уровня (в изолированном атоме на
нем находятся валентные электроны). Число возможных кван-
товых состояний в валентной зоне больше числа электронов,
поэтому часть энергетических уровней оказываются свобод –
ными. Валентную зону в металлах и сплавах называют еще
зоной проводимости, поскольку электроны именно этой зоны
ответственны за тепло- и электропроводность в указанных
материалах. Заполнение валентной зоны начинается с самых
низких уровней. Итак, свободные электроны в металле обла-
дают одинаковой потенциальной, но разной кинетической, а
следовательно, и полной энергией.
Слайд 117Если классические частицы должны при температуре 0 К за-
нимать нулевой
неподвижны, то по квантовой теории это невозможно(принцип
Паули) и электроны при 0 К обладают колоссальной энергией
не теплового происхождения. Максимальная кинетическая
Энергия свободных электронов называется энергией Ферми.
На рисунке схематично изо-
бражены энергетические зо-
ны металла, п/проводника и
диэлектрика. При Т≠ 0 К в зо
не проводимости п/провод-
ника появляются электрон-
ны. Их появление обуслов-
лено тепловым движением.
Слайд 118Функция распределения электронов по энергетическим состоя
ниям была найдена Ферми и Дираком.
Густота
деляется плотностью состояний. Плотность состояний - это
число возможных квантовых состояний, приходящихся на
единичный интервал энергии в единице объемы металла.
Следует отметить, что кинетические свойства электронной
подсистемы определяются электронами, находящимися вбли
зи уровня Ферми.
Слайд 119Теплоемкость электронов в металле и п/проводнике
В рамках классической электронной теории Друде
рассматривая электроны как идеальный газ, молярную элек-
тронную теплоемкость можно определить:
CVЭЛ = (3/2)R.
В 1028 г. А.Зоммерфельд предложил модель, согласно кото-
рой распределение свободных электронов в металле описы-
вается распределением Ферми - Дирака, а нераспределени-
ем Больцмана, как это следует из теории Друде. В рамках мо-
дели Зоммерфельда
CVЭЛ = ((πk)2NА/2µ)T = γТ,
где NА – число Авогадро, µ - энергия Ферми, γ – коэффициент
электронной теплоемкости.
Слайд 120
ти связан с плотностью электронных состояний вблизи уровня
Ферми g0(µ) (при Т = 0 К) выражением:
γ = (2/3) (πk)2 g0(µ).
Таким образом, для молярной теплоемкости металла CV име
ем при низких температурах (Т ≤ ӨD/12):
CV = CVЭЛ + CVРЕШ = γТ + βТ3.
Особенности электронного строения переходных металлов и
их соединений, обладающих высокой плотностью электрон-
ных состояний вблизи уровня Ферми, приводят к тому, что
температурные зависимости электронной теплоемкости этих
материалов в области низких температур могут носить не тра-
диционный характер.
Слайд 121Так, в рамках модели Лаббе - Фриделя для случая почти пус-
той
ронная теплоемкость пропорциональна температуре и может
быть описана выражением:
CVЭЛ = (π2/6kQTµ}T,
Где Q – число электронов, содержащихся в рассматриваемой
подполосе, а Tµ - температура Ферми.
При этом высокотемпературный предел электронной тепло-
емкости оказывается равным:
CVЭЛ ∞ = (1/2) kQ.
Подобное поведение теплоемкости электронов может быть
связано с весьма низкой температурой снятия вырождения.
Температурный интервал, пределах которого меняется элек-
тронная теплоемкость от CVЭЛ = γТ до CVЭЛ ∞ = const весьма
узок.