- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Стационарные процессы теплопроводности (продолжение) презентация
Содержание
- 1. Стационарные процессы теплопроводности (продолжение)
- 2. Дифференциальное уравнение теплопроводности изменение
- 3. Распределение температуры в пластине
- 4. Распределение температуры в пластине
- 5. Распределение температуры в пластине
- 6. Распределение температуры в пластине с
- 7. Распределение температуры в пластине с
- 8. Распределение температуры в пластине с
- 9. Распределение температуры в пластине с
- 10. Частный случай Перепад
- 11. Распределение температуры в пластине с
- 12. Распределение температуры в пластине с
- 13. Частный случай - нет внутреннего
- 14. Частный случай - 2
- 15. Поле температуры в цилиндрической стенке
- 16. Поле температуры в цилиндрической стенке
- 17. Поле температуры в цилиндрической стенке
- 18. Поле температуры в цилиндрической стенке с
- 19. Поле температуры в цилиндрической стенке с
- 20. Поле температуры в сплошном цилиндре
- 21. Поле температуры в сплошном цилиндре
- 22. Поле температуры в шаре с тепловыделением
- 23. Поле температуры в шаре с тепловыделением
- 24. из граничных условий Распределение
- 28. Перенос тепла в ребрах Через
- 39. Учет зависимости теплопроводности от температуры
- 40. Учет зависимости теплопроводности от температуры
- 41. Учет зависимости теплопроводности от температуры (цилиндрическая геометрия)
- 44. Обмуровка трубопроводов Хромитовая масса
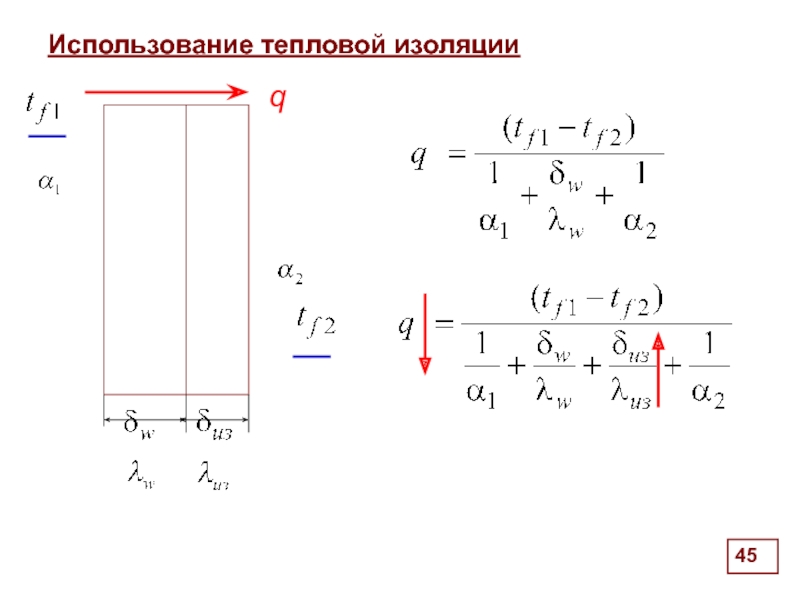
- 45. Использование тепловой изоляции q
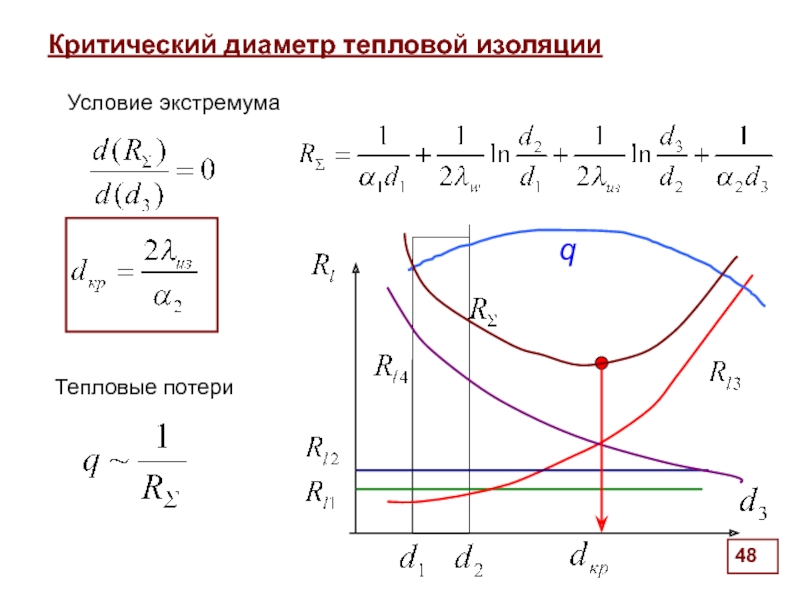
- 46. Критический диаметр тепловой изоляции
- 47. Критический диаметр тепловой изоляции
- 48. Критический диаметр тепловой изоляции
- 49. Критический диаметр тепловой изоляции
Слайд 2
Дифференциальное уравнение теплопроводности
изменение
температуры
во времени
изменение темп. поля,
вызванное движением среды
изменение темп.
поля
в
интенсивность
внутренних
источников тепла
Слайд 3
Распределение температуры в пластине
стационарная
задача
0
0
неподвижная
среда
0
нет внутреннего
тепловыделения
Найти:
стационарное распределение температуры
в пластине
без внутреннего тепловыделения
при Г.У. 1 рода
Слайд 4
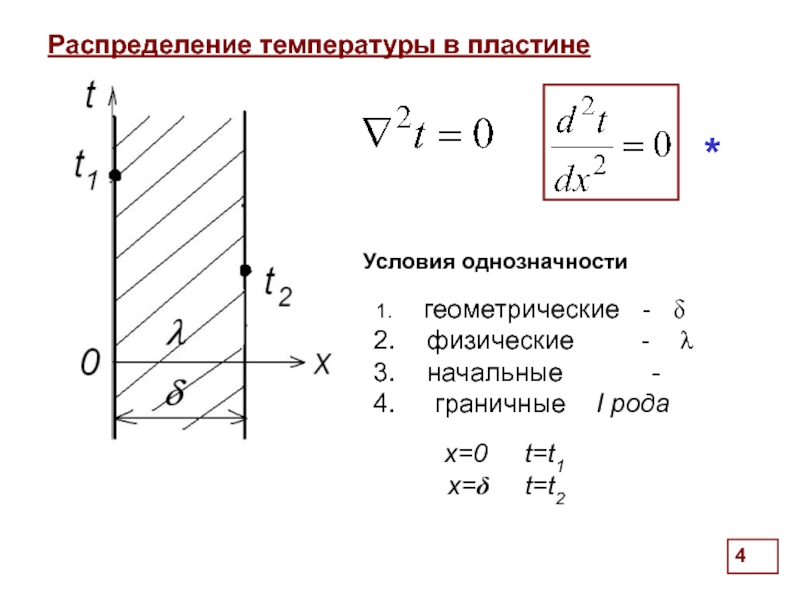
Распределение температуры в пластине
геометрические - δ
физические
начальные -
граничные I рода
x=0 t=t1
x=δ t=t2
Условия однозначности
*
Слайд 5
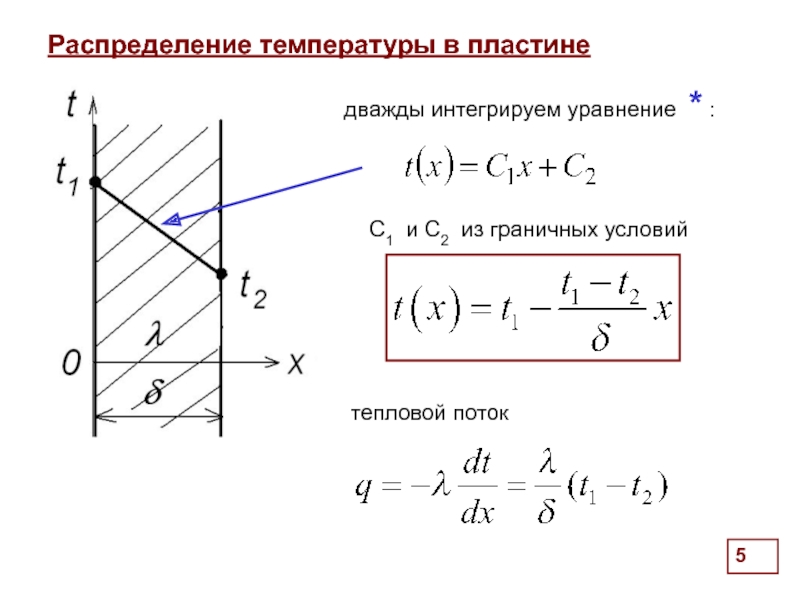
Распределение температуры в пластине
дважды интегрируем уравнение * :
С1 и
тепловой поток
Слайд 6
Распределение температуры в пластине с внутренним тепловыделением
дифференциальное уравнение теплопроводности
температура
Бесконечная плоская пластина толщиной с внутренними источниками тепла Вт/м3, равномерно распределенными по сечению
Слайд 7
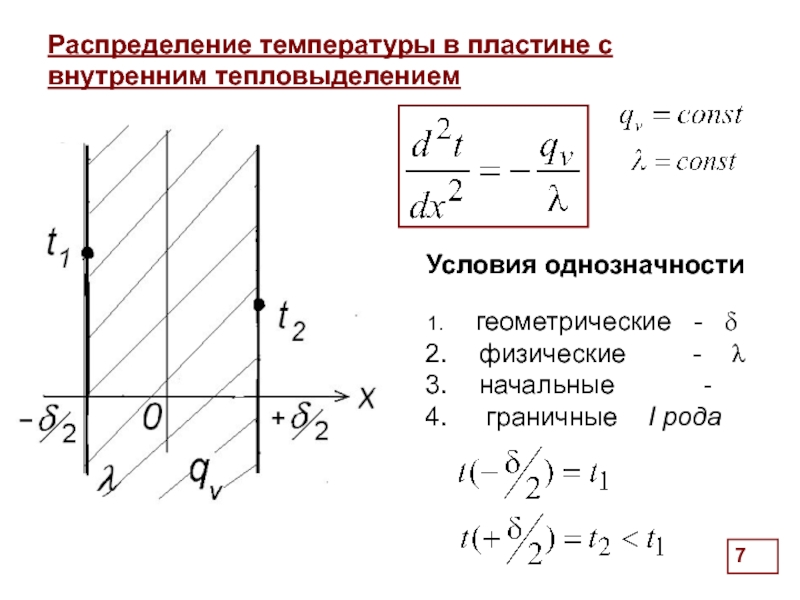
Распределение температуры в пластине с внутренним тепловыделением
геометрические -
физические - λ
начальные -
граничные I рода
Условия однозначности
Слайд 8
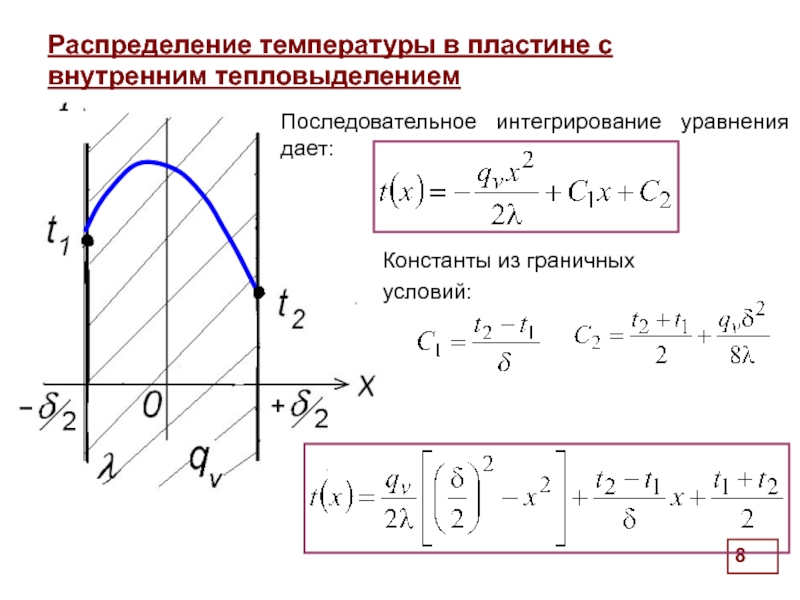
Распределение температуры в пластине с внутренним тепловыделением
Последовательное интегрирование уравнения дает:
Константы из граничных условий:
Слайд 9
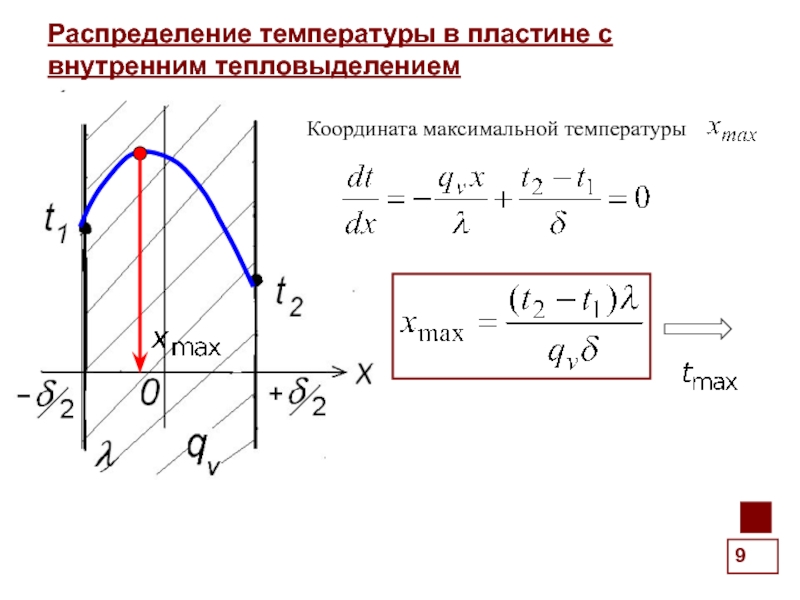
Распределение температуры в пластине с внутренним тепловыделением
Координата максимальной температуры
Слайд 11
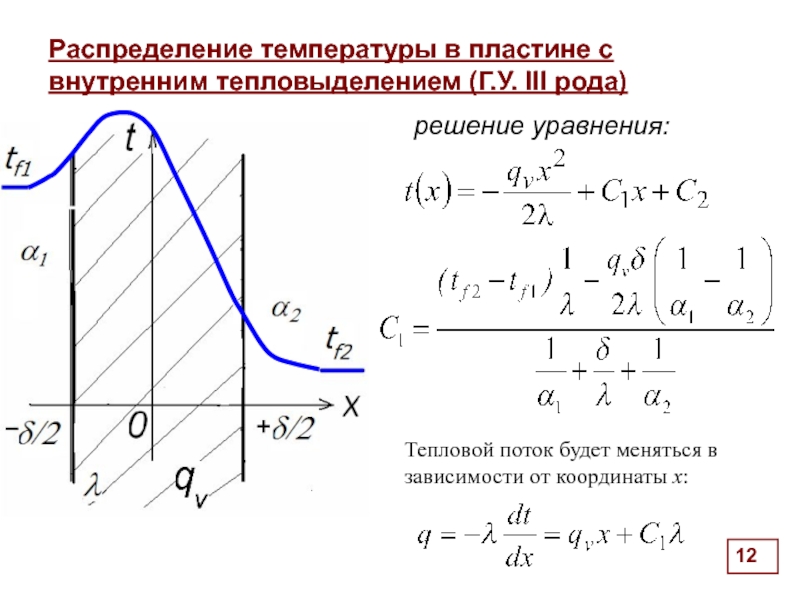
Распределение температуры в пластине с внутренним тепловыделением (Г.У. III рода)
граничные условия
заданы коэффициенты теплообмена на границах и температуры жидкостей, омывающих поверхности
Слайд 12
Распределение температуры в пластине с внутренним тепловыделением (Г.У. III рода)
решение уравнения:
Тепловой
Слайд 13
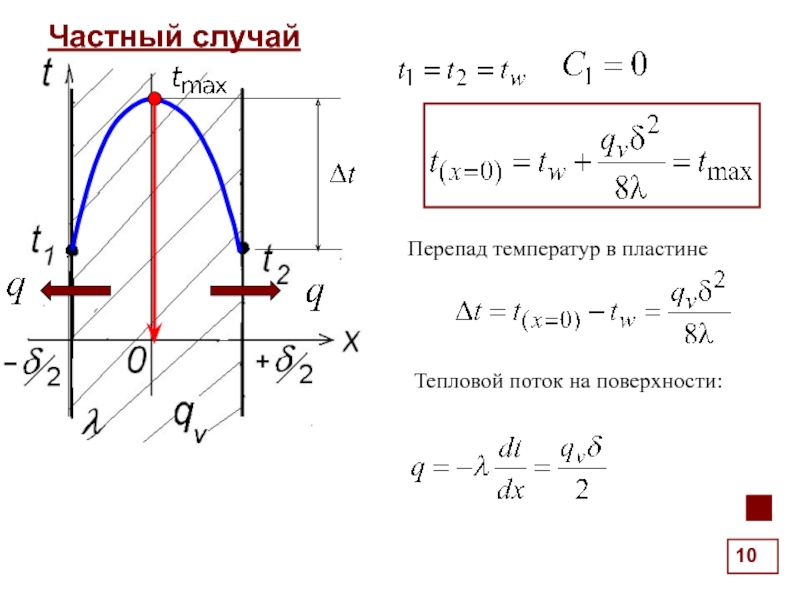
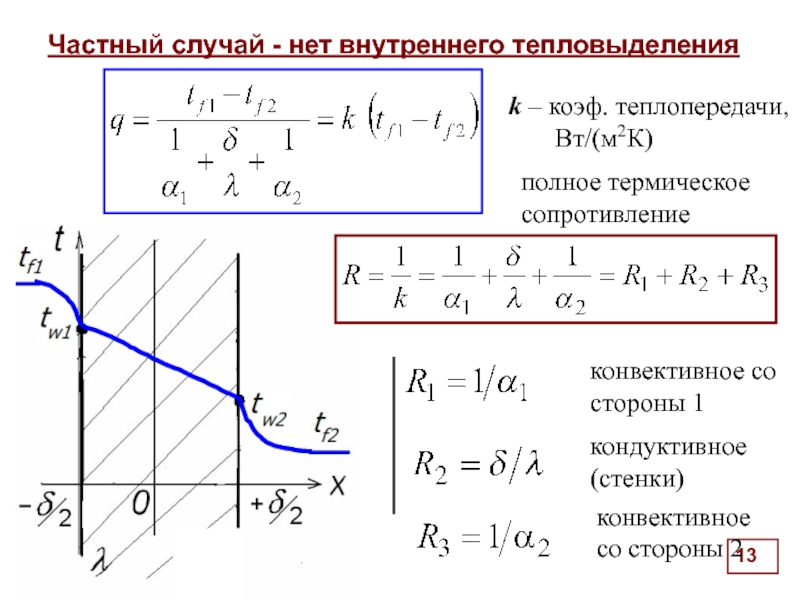
Частный случай - нет внутреннего тепловыделения
полное термическое сопротивление
конвективное со стороны 1
кондуктивное
конвективное со стороны 2
k – коэф. теплопередачи,
Вт/(м2К)
Слайд 14
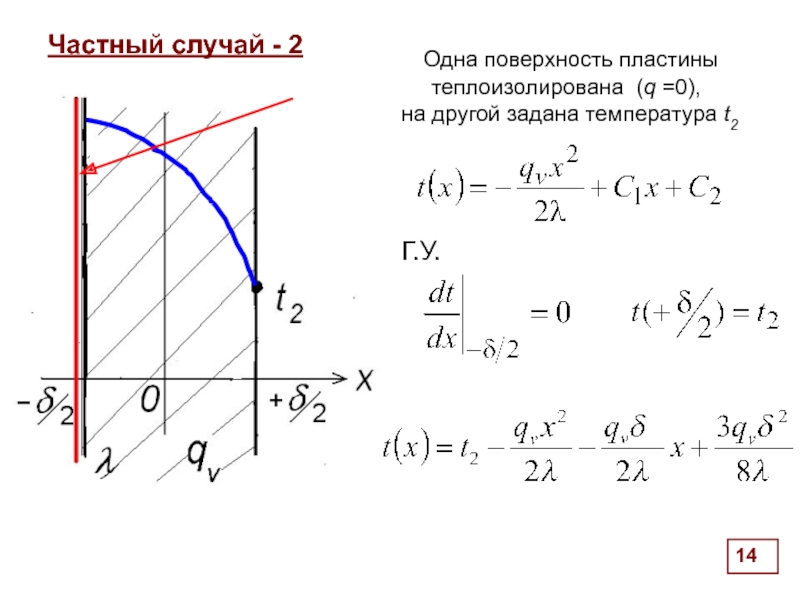
Частный случай - 2
Одна поверхность пластины теплоизолирована (q =0),
на другой задана температура t2
Г.У.
Слайд 15
Поле температуры в цилиндрической стенке без тепловыделения
геометрические - r1,
физические - λ
начальные -
граничные I рода
Условия однозначности
Слайд 17
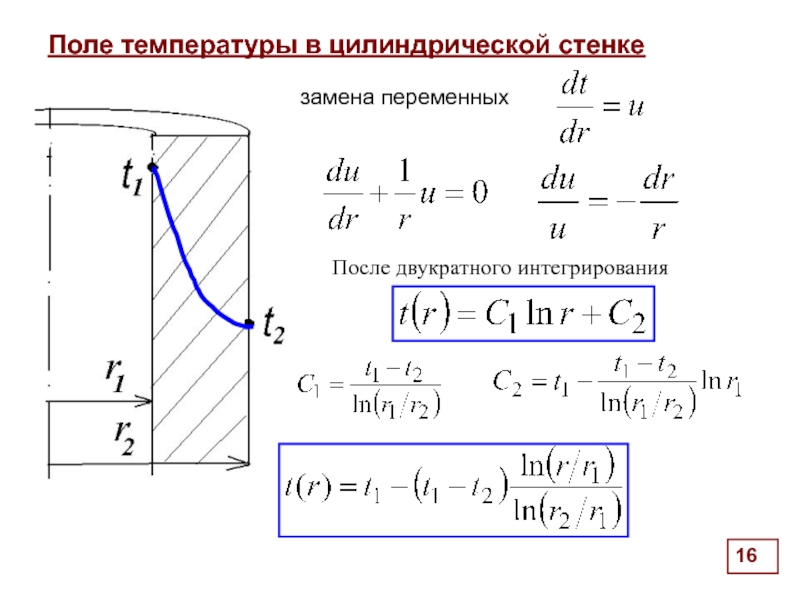
Поле температуры в цилиндрической стенке
Логарифмический закон изменения температуры по радиусу является
Количество тепла, проходящее через цилиндрическую поверхность
в единицу времени
Тепловой поток, отнесенный к единице длины трубы (линейный тепловой поток)
из решения уравнения
Слайд 18
Поле температуры в цилиндрической стенке с внутренним тепловыделением
цилиндрическая стенка с внутренним
наружным r2 , с постоянным коэффициентом
теплопроводности и равномерно распределенными
источниками тепла
при
или
при
используем метод подстановки
умножаем на
tf
Слайд 19
Поле температуры в цилиндрической стенке с внутренним тепловыделением
Подставляем сюда r1
Из второго
Распределение температуры в цилиндрической стенке при заданных Г.У.
Температура внешней поверхности
Плотность теплового потока на r2
Перепад температур в стенке
Слайд 20
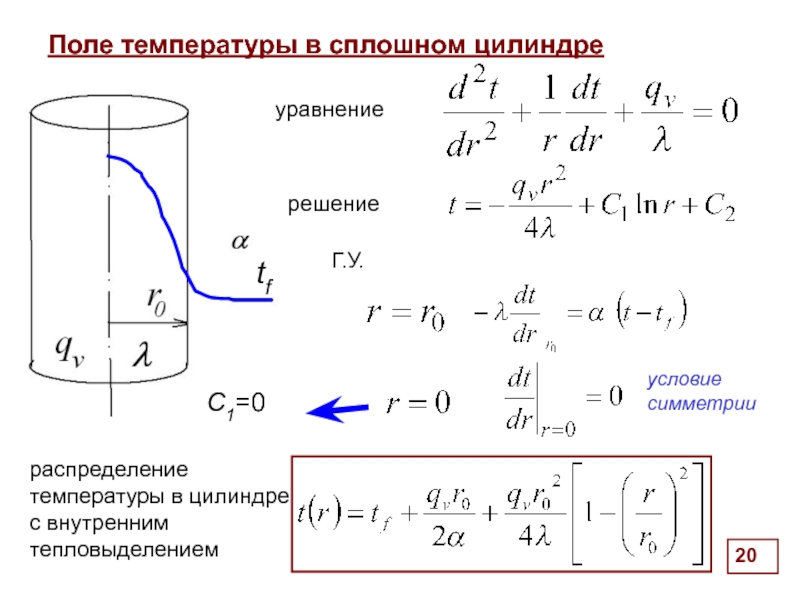
Поле температуры в сплошном цилиндре
распределение температуры в цилиндре
с внутренним тепловыделением
С1=0
условие симметрии
tf
уравнение
решение
Г.У.
Слайд 21
Поле температуры в сплошном цилиндре
температура внешней поверхности цилиндра
перепад температур в цилиндре
плотность теплового потока на поверхности цилиндра
tf
Слайд 22
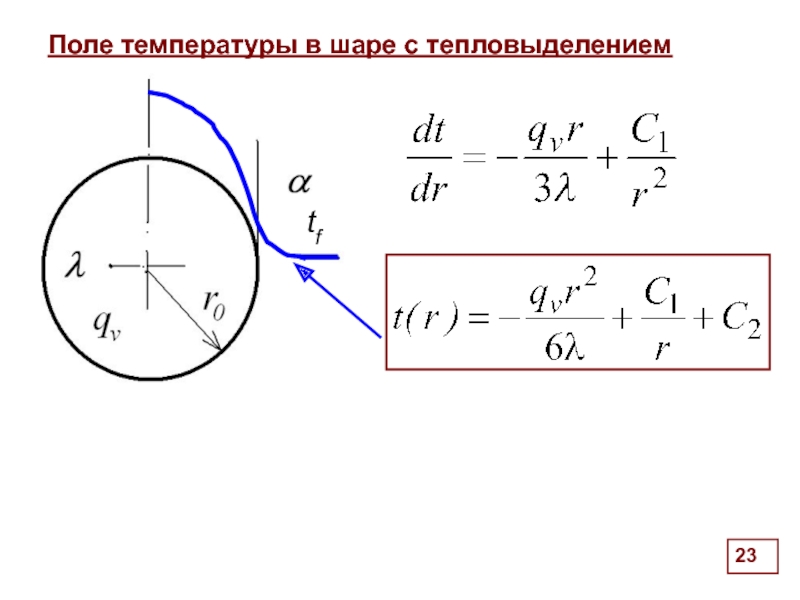
Поле температуры в шаре с тепловыделением
Граничные условия:
*
подстановка
умножение всех членов уравнения (*) на
tf
Слайд 24из граничных условий
Распределение температур в шаре:
перепад температур в
плотность теплового потока
на поверхности шара
Поле температуры в шаре с тепловыделением
Слайд 25
Перенос тепла в ребрах
Закон Ньютона-Рихмана
Увеличение поверхности теплообмена - оребрение
Слайд 26
Перенос тепла в ребрах
Через сечение x передается количество тепла:
Кипящая вода
Свободная конвекция в воздухе
полное термическое сопротивление
Полное термическое сопротивление имеет порядок большего термического сопротивления, там и делают оребрение
пренебрегаем
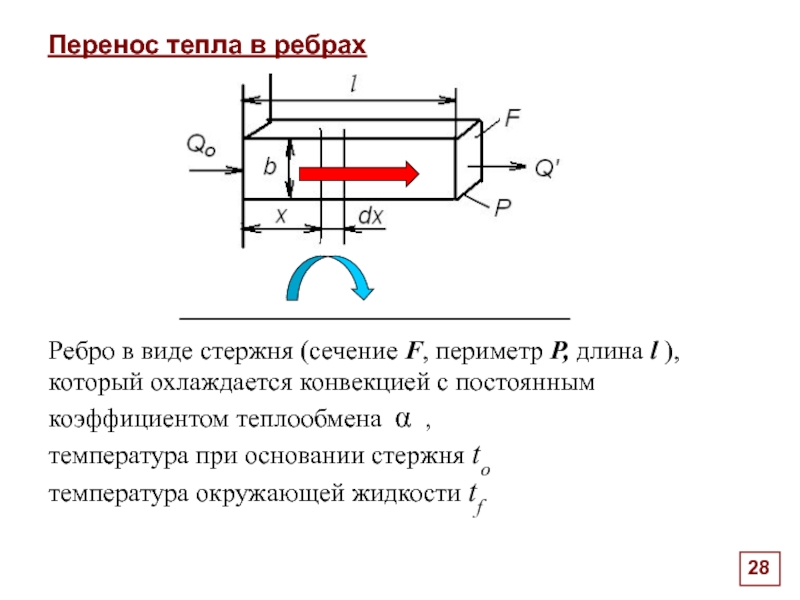
Слайд 28Перенос тепла в ребрах
Через сечение x передается количество тепла:
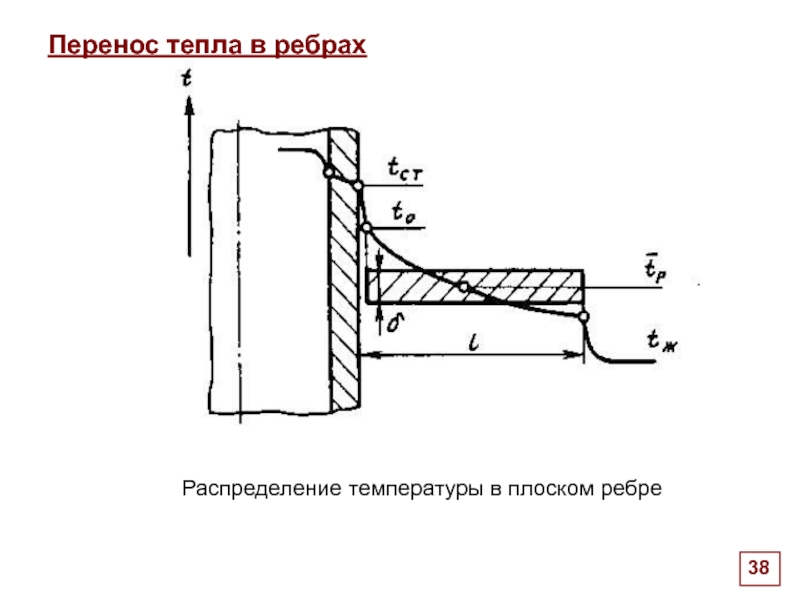
Ребро в виде стержня (сечение F, периметр P, длина l ), который охлаждается конвекцией с постоянным коэффициентом теплообмена α ,
температура при основании стержня to
температура окружающей жидкости tf
Слайд 29
Перенос тепла в ребрах
Через сечение x передается количество тепла:
На длине dx отводится тепло конвекцией,
изменение потока тепла
По закону Ньютона-Рихмана
Через сечение х передается количество тепла
Слайд 30
Перенос тепла в ребрах
Через сечение x передается количество тепла:
Частное решение уравнения:
Общее решение
Вводим переменную
Слайд 31
Перенос тепла в ребрах
Через сечение x передается количество тепла:
С1 и С2 определяются из Г.У., которые могут быть
различными в зависимости от длины ребра и его формы.
Число Био
(Biot)
Если длина стержня больше его толщины, то отводом тепла с торца (Q') можно пренебречь
эквивалентный диаметр
при
w
Слайд 32
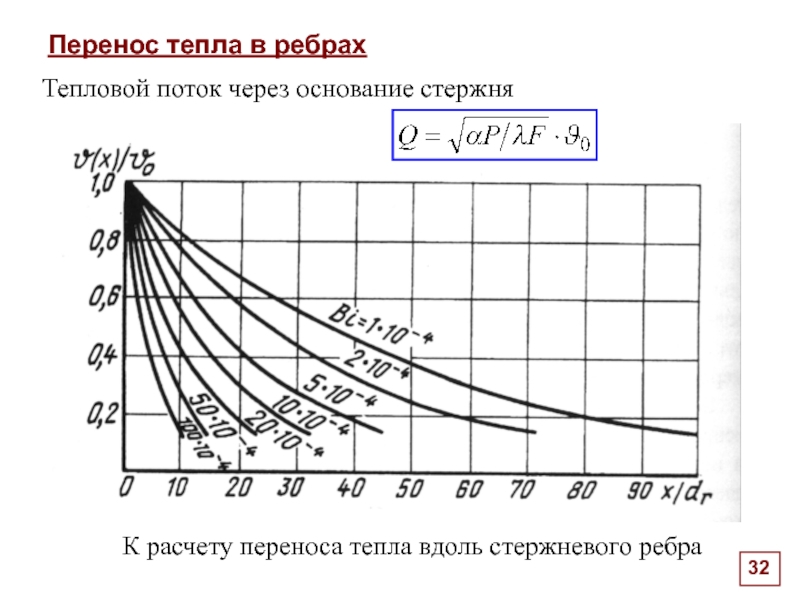
Перенос тепла в ребрах
К расчету переноса тепла вдоль стержневого ребра
Тепловой поток через основание стержня
Слайд 33
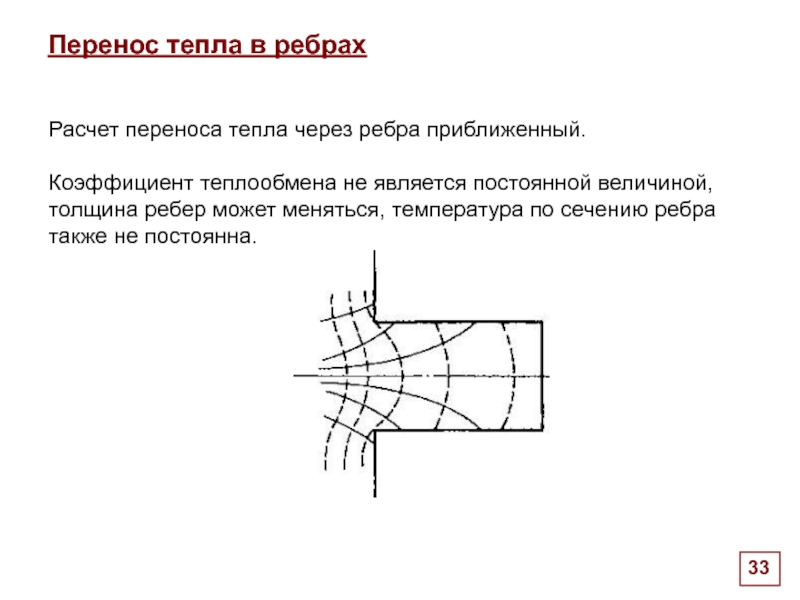
Перенос тепла в ребрах
Через сечение x передается количество тепла:
Расчет переноса тепла через ребра приближенный.
Коэффициент теплообмена не является постоянной величиной, толщина ребер может меняться, температура по сечению ребра также не постоянна.
Слайд 34
Перенос тепла в ребрах
Коэффициент эффективности ребра - отношение теплового потока от ребра ( ) к тепловому потоку от идеального ребра с бесконечно большим коэффициентом теплопроводности ( ):
Допущение о бесконечно большой теплопроводности приводит к выводу, что температура ребра по длине будет постоянной
Слайд 35
Перенос тепла в ребрах
Через сечение x передается количество тепла:
Коэффициент эффективности ребра с постоянным поперечным сечением и тепловой изоляцией на торце
комплекс, имеющий размерность длины
Критерий Био
термическое сопротивление ребра
конвективное термическое сопротивление
Слайд 36
Перенос тепла в ребрах
быстро снижается с ростом числа Bi.
Ребро с большим значением Bi рассеивает тепло хуже, чем ребро с меньшим числом Bi
для ребер надо выбирать материал с высокой теплопроводностью
Если мал, то поверхность без ребра будет отдавать тепло
более интенсивно, чем поверхность с ребрами.
При больших Bi кондуктивное термическое сопротивление велико
по сравнению с конвективным термическим сопротивлением, и поэтому температура существенно падает вдоль ребра.
Если Bi велико, то площадь, занятая ребрами с малой тепло-
проводностью, "изолирует" поверхность отвода тепла.
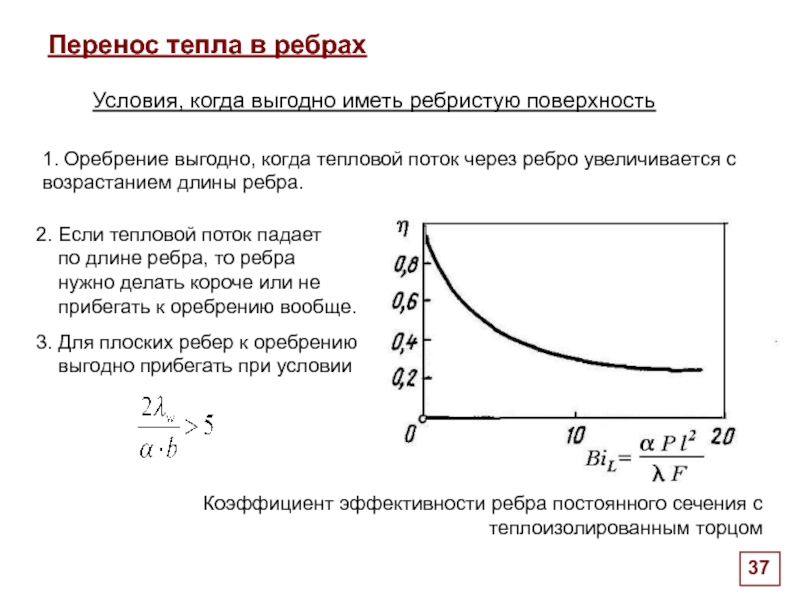
Важно установить условия, когда выгодно иметь
ребристую поверхность
?
Слайд 37
Перенос тепла в ребрах
Коэффициент эффективности ребра постоянного сечения с теплоизолированным торцом
3. Для плоских ребер к оребрению
выгодно прибегать при условии
Условия, когда выгодно иметь ребристую поверхность
1. Оребрение выгодно, когда тепловой поток через ребро увеличивается с возрастанием длины ребра.
2. Если тепловой поток падает
по длине ребра, то ребра
нужно делать короче или не
прибегать к оребрению вообще.
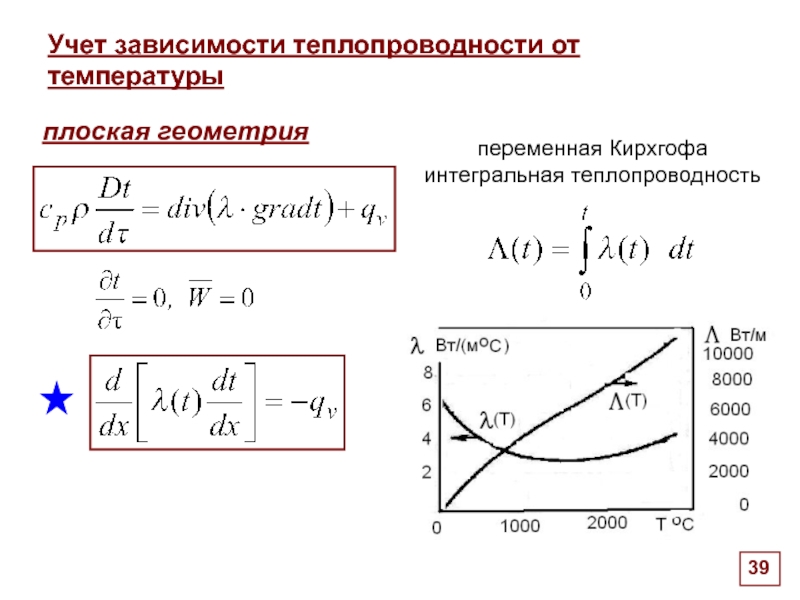
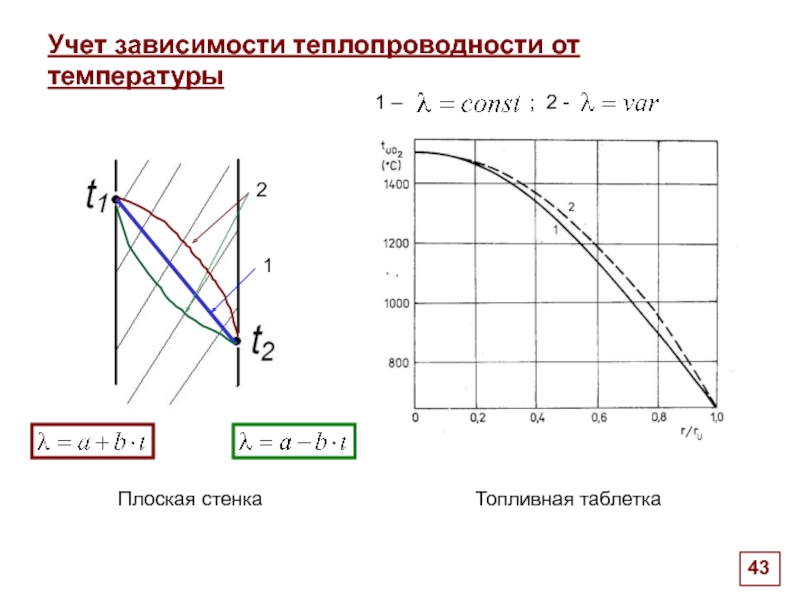
Слайд 39Учет зависимости теплопроводности от температуры
переменная Кирхгофа
интегральная теплопроводность
плоская геометрия
Слайд 40Учет зависимости теплопроводности от температуры
решаем относительно , затем находим температуру
Т.к. производная от интеграла по верхнему пределу
есть подинтегральная функция, т.е.
Слайд 41Учет зависимости теплопроводности от температуры (цилиндрическая геометрия)
уравнение теплопроводности для сплошного цилиндра
(таблетка топлива радиусом R)
с переменным
тепловыделением :
После интегрирования
обеих частей уравнения в пределах от 0 до r :
Интегрирование в пределах
от r до R :
Для постоянного тепловыделения:
.
Слайд 42
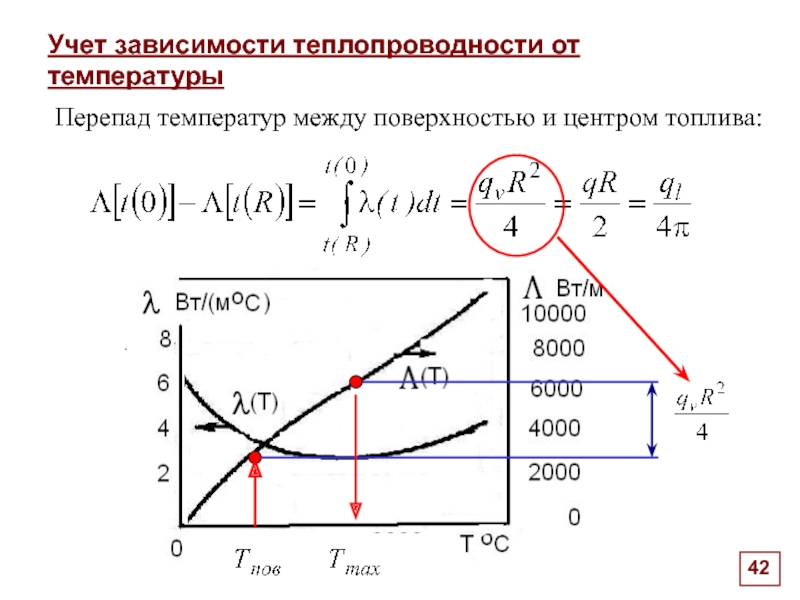
Учет зависимости теплопроводности от температуры
Перепад температур между поверхностью и центром топлива:
.
Слайд 43
Учет зависимости теплопроводности от температуры
Топливная таблетка
1 – ; 2 -
Плоская стенка
1
2
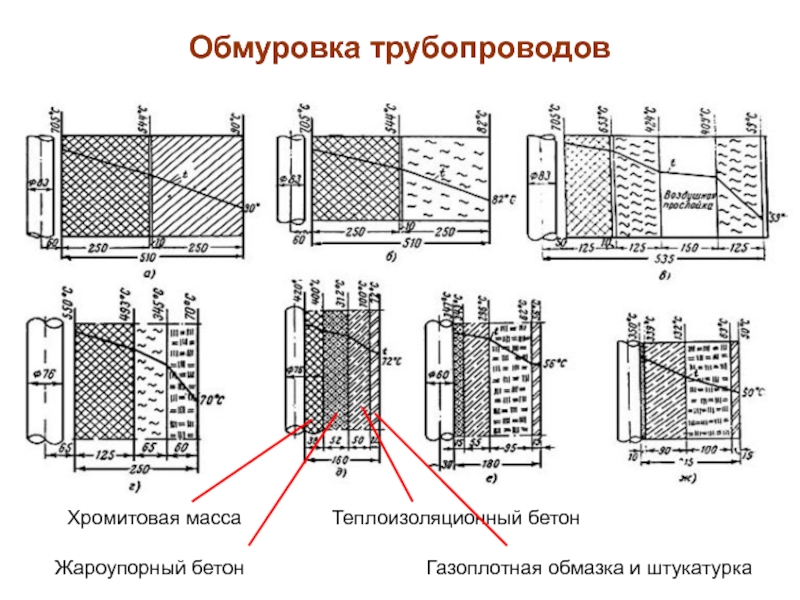
Слайд 44Обмуровка трубопроводов
Хромитовая масса
Жароупорный бетон
Теплоизоляционный бетон
Газоплотная
Слайд 49
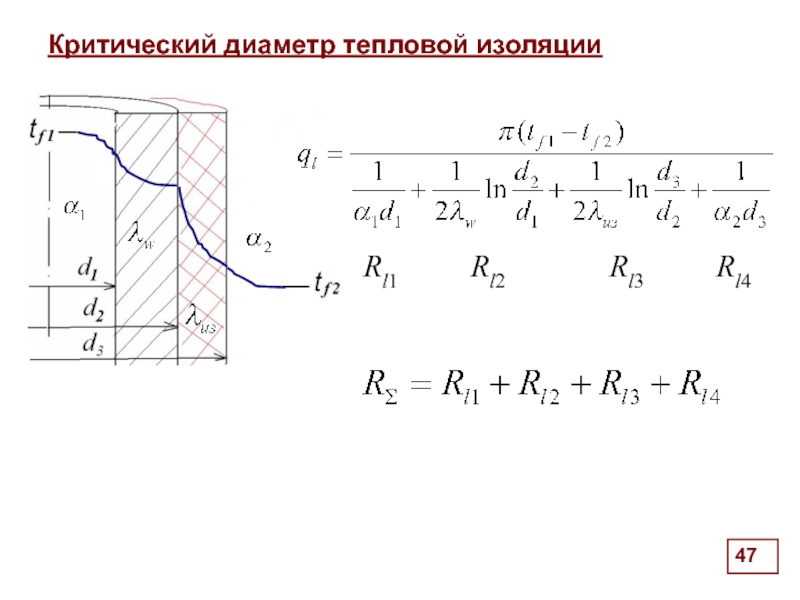
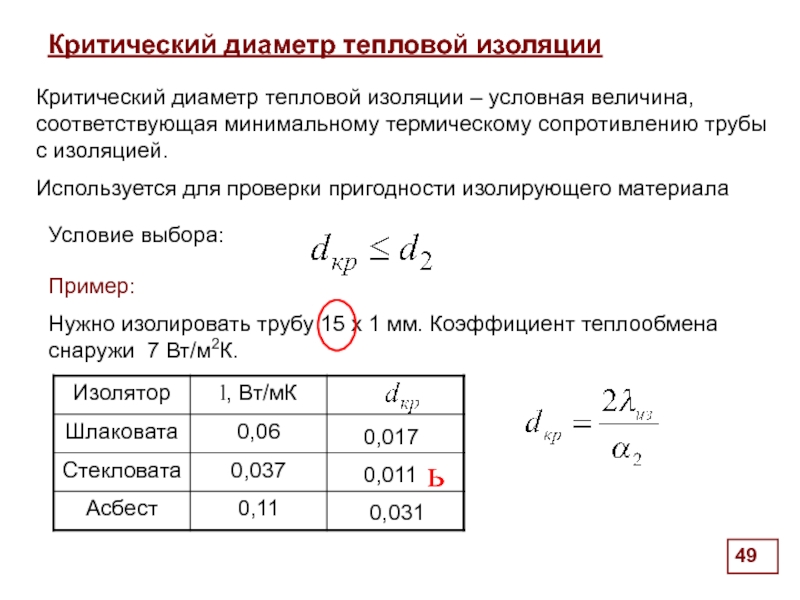
Критический диаметр тепловой изоляции
Критический диаметр тепловой изоляции – условная величина, соответствующая
Используется для проверки пригодности изолирующего материала
Пример:
Нужно изолировать трубу 15 х 1 мм. Коэффициент теплообмена снаружи 7 Вт/м2К.
0,017
0,011
0,031
Условие выбора:
ь