- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Статика. Виды равновесия. Равновесие тел имеющих площадь опоры. Законы равновесия. (10 класс) презентация
Содержание
- 1. Статика. Виды равновесия. Равновесие тел имеющих площадь опоры. Законы равновесия. (10 класс)
- 2. Содержание Статика Первое условие равновесия Момент
- 3. Статика Раздел механики, в котором изучается
- 4. Первое условие равновесия Твердое тело находится
- 5. Задача №1 Электрическая лампа подвешена на шнуре
- 6. А В Задача №2 К концу двухметрового
- 7. Задача №3 На бельевой веревке длиной 10м
- 8. А В С Задача №4 Найти
- 9. 2 3 4 y х 1-ый
- 10. Задача №1 2 3 4
- 11. А В Задача №2 С
- 12. Задача №3 ℓ/2
- 13. А В С Задача №4
- 14. Момент силы Правило моментов 10 класс
- 15. Что такое равновесие? Как читается условие равновесия абсолютно твердого тела?
- 16. Второе условие равновесия Кратчайшее расстояние от оси
- 17. Плечо силы Однородный куб опирается одним ребром
- 18. Момент силы Чему равен момент силы
- 19. Второе условие равновесия Твердое тело находится в
- 20. Условия равновесия Твердое тело находится в равновесии,
- 21. Задача №1 Электрическая лампа подвешена на шнуре
- 22. Задача №6 К балке массой 200кг и
- 23. Задача №1 Дано: m=1кг α= 60о 2
- 24. Задача №6 АВ=5м М=200кг m=250кг АС=3м
- 25. Виды равновесия 10 класс
- 26. Что такое равновесие? При каком условии
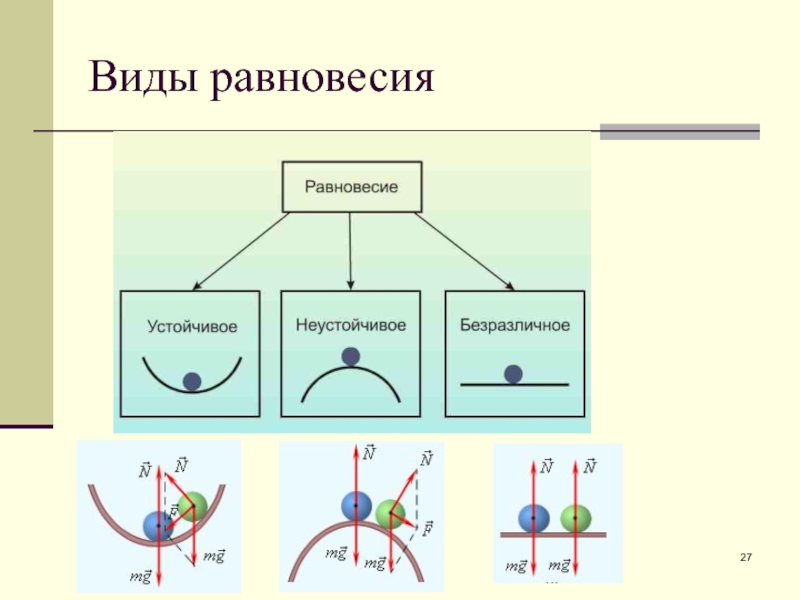
- 27. Виды равновесия
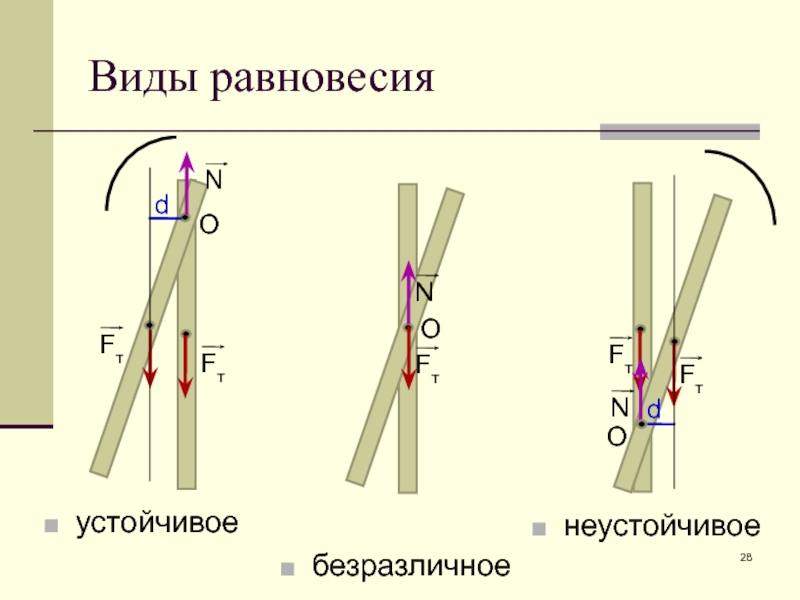
- 28. устойчивое d Виды равновесия неустойчивое безразличное О d
- 29. Условия устойчивости равновесия Тела находятся в состоянии
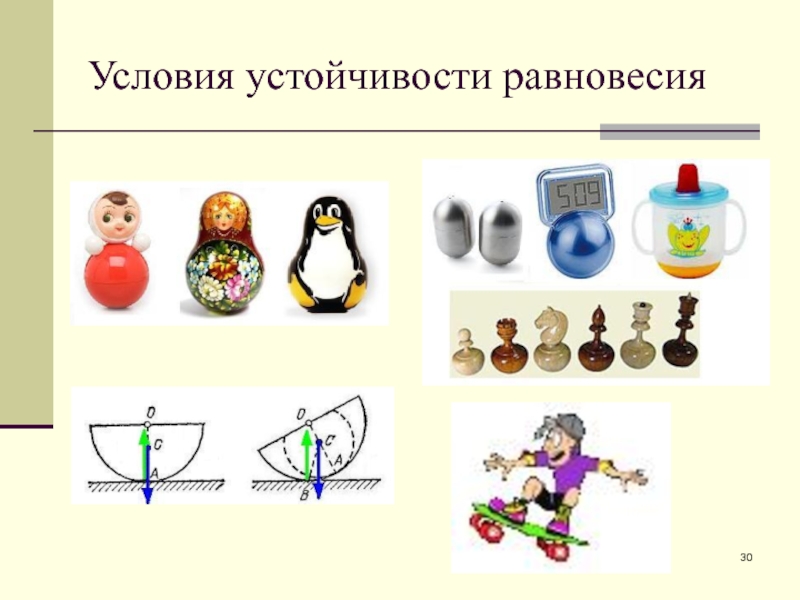
- 30. Условия устойчивости равновесия
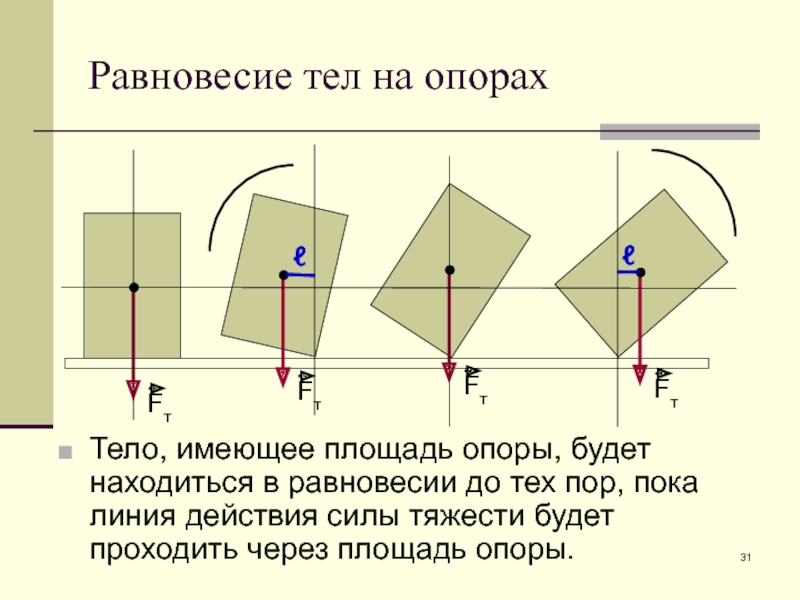
- 31. Равновесие тел на опорах Тело, имеющее
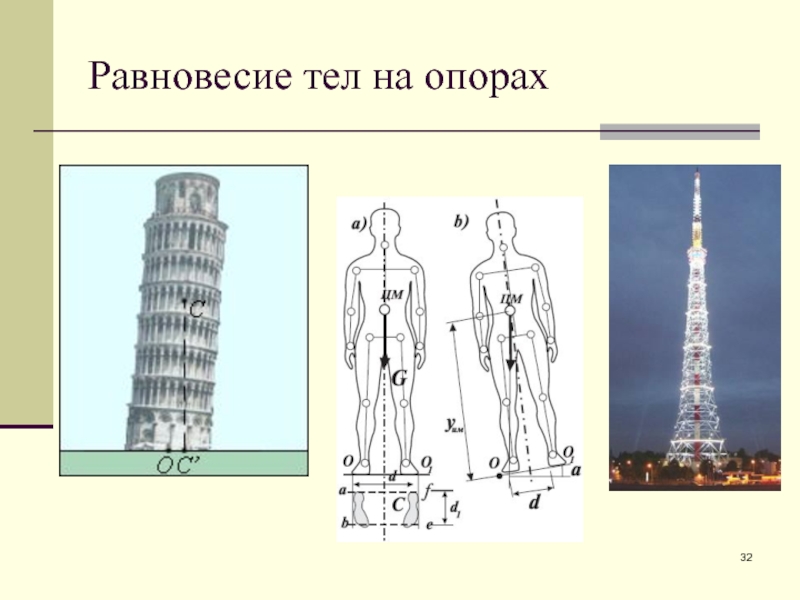
- 32. Равновесие тел на опорах
- 33. Устойчивость транспорта
- 34. Решение задач по теме «Статика»
- 35. На столе лежат три книги. Значения сил
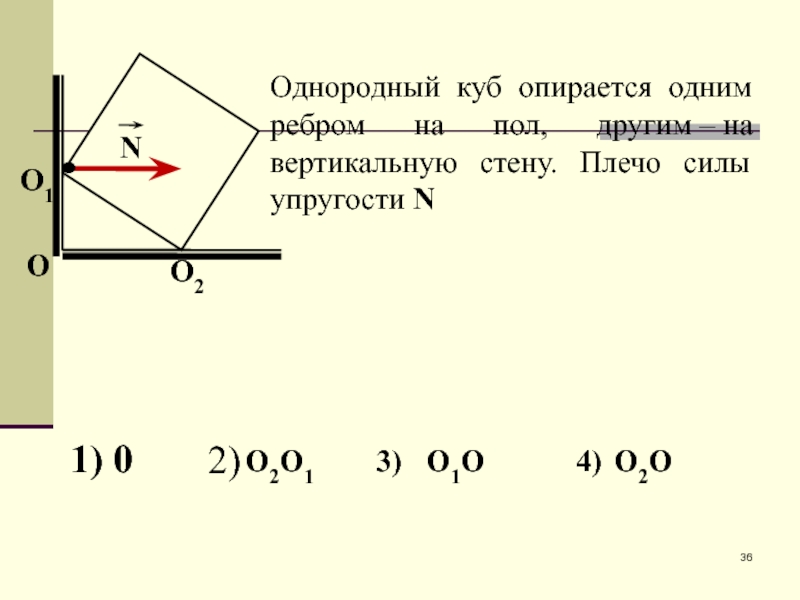
- 36. Однородный куб опирается одним ребром на пол,
- 37. Труба массой М = 1
- 38. На рисунке схематически изображена металлическая труба, прислонённая
- 39. Чему равен момент силы тяжести груза массой
- 40. При решении задач на равновесие тел:
- 41. К гвоздю, вбитому в стенку, привязана нить,
- 42. Решение: Изобразим силы, действующие на катушку на
- 43. Цилиндр массой m = 150 кг удерживается
- 44. 2T + mg + N =
- 45. Задача №3 Однородный шар радиуса R подвешен
- 46. mg N Fтр T Α Решение:
- 47. Задача №4. Какой минимальной горизонтальной силой можно
- 48. F O mg Fтр N Решение:
- 49. Тонкостенная полусфера массой M и радиусом R
- 50. Решение: Под действием веса мухи полусфера
Слайд 2Содержание
Статика
Первое условие равновесия
Момент силы
Второе условие равновесия
Виды равновесия
Равновесие тел имеющих площадь
Слайд 3Статика
Раздел механики, в котором изучается равновесие абсолютно твердых тел, называется
Равновесие тела – это состояние покоя или равномерного и прямолинейного движения тела.
Абсолютно твердое тело – тело, у которого деформации, возникающие под действием приложенных к нему сил, пренебрежимо малы.
Слайд 4
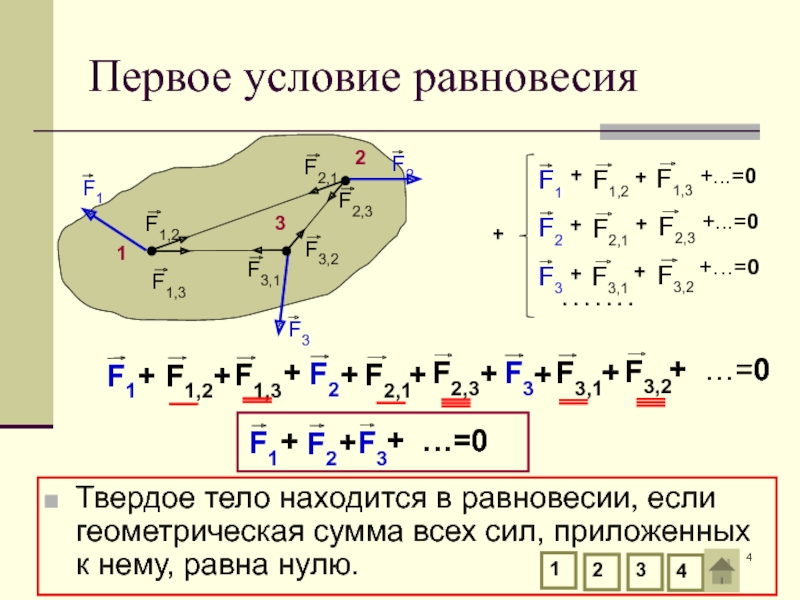
Первое условие равновесия
Твердое тело находится в равновесии, если геометрическая сумма всех
1
2
3
+
. . . . . . .
1
2
3
4
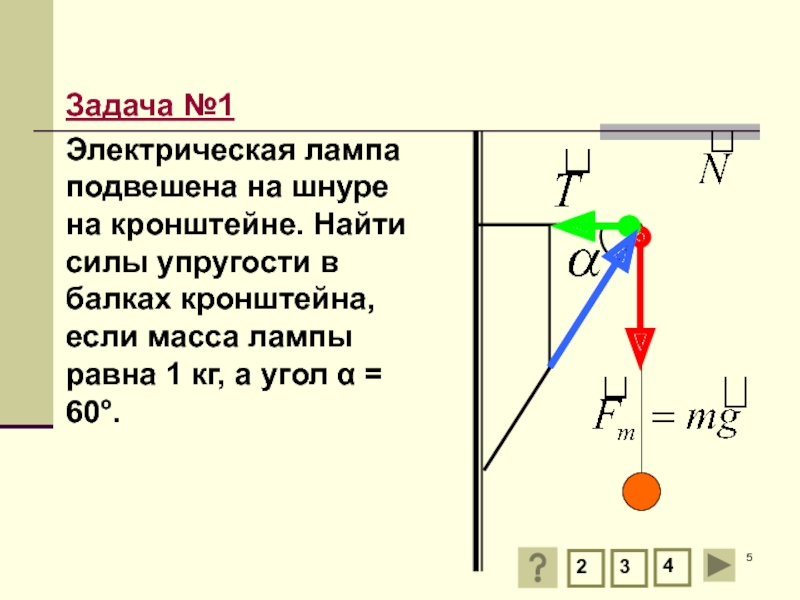
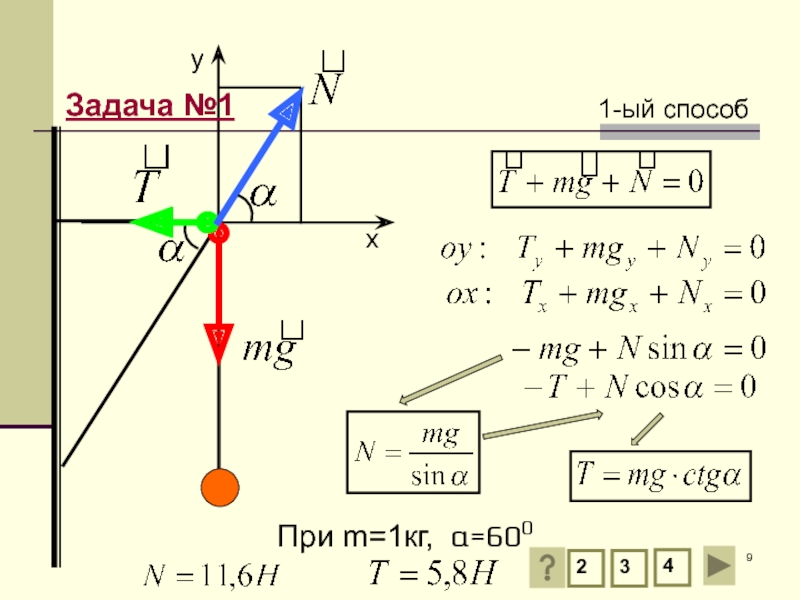
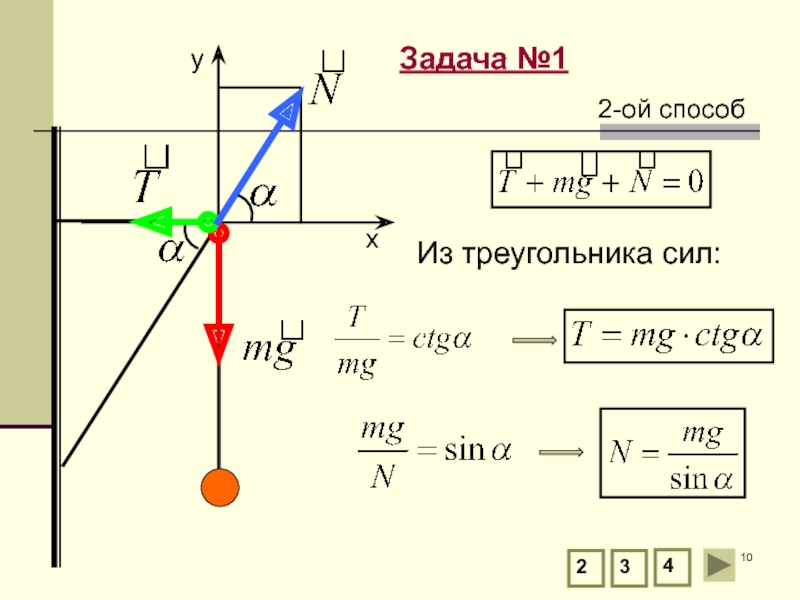
Слайд 5Задача №1
Электрическая лампа подвешена на шнуре на кронштейне. Найти силы упругости
2
3
4
Слайд 6А
В
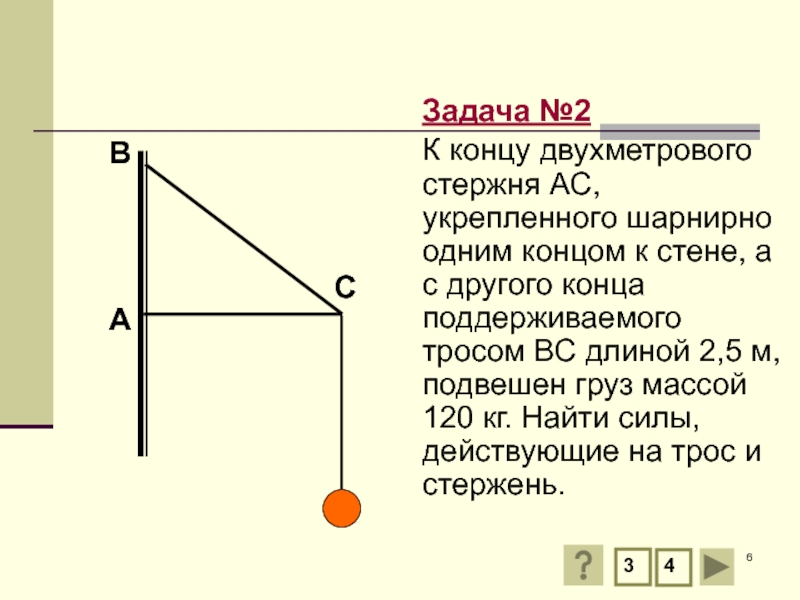
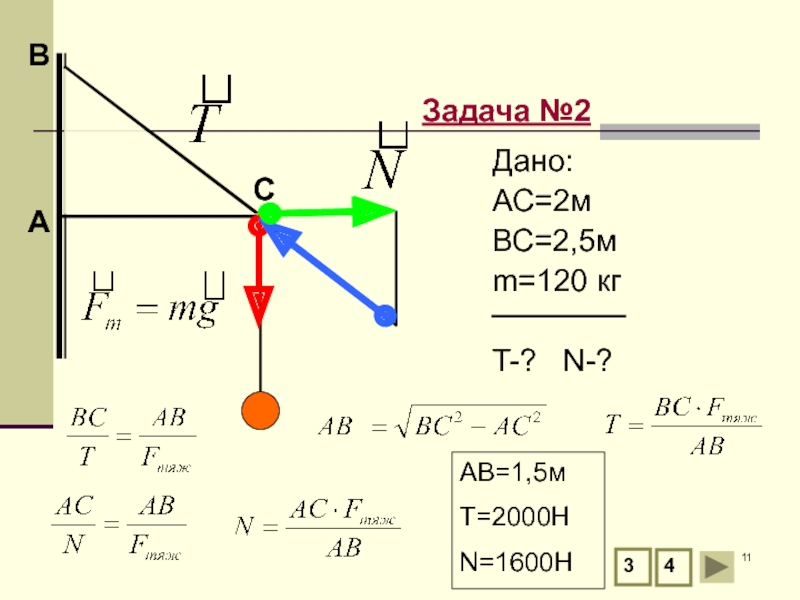
Задача №2
К концу двухметрового стержня АС, укрепленного шарнирно одним концом к
С
3
4
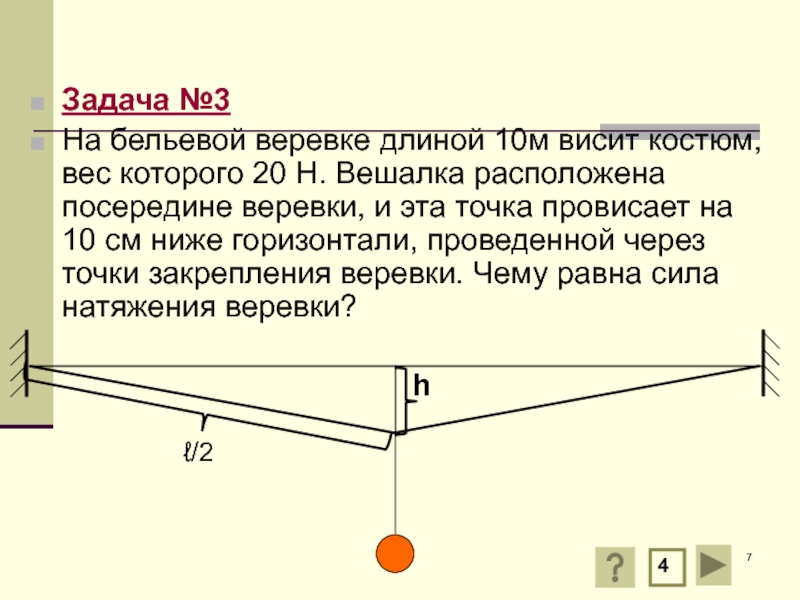
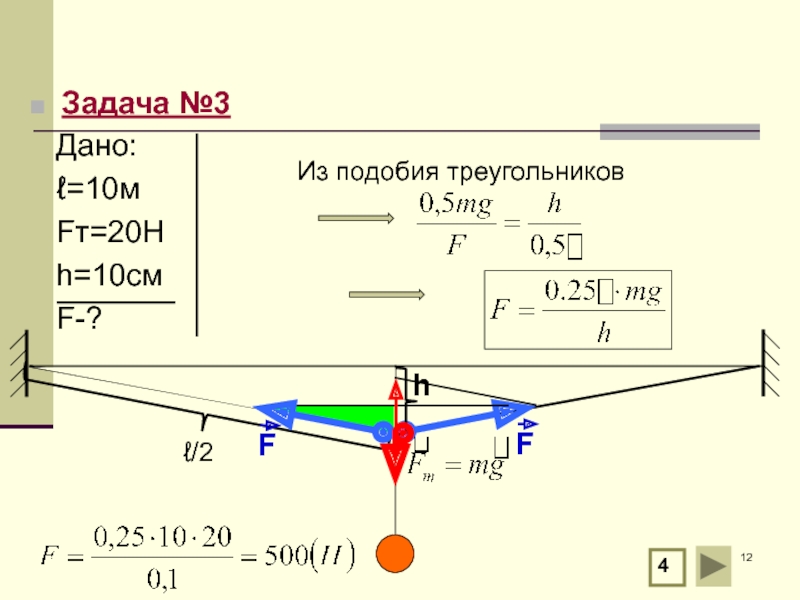
Слайд 7Задача №3
На бельевой веревке длиной 10м висит костюм, вес которого 20
ℓ/2
4
Слайд 8
А
В
С
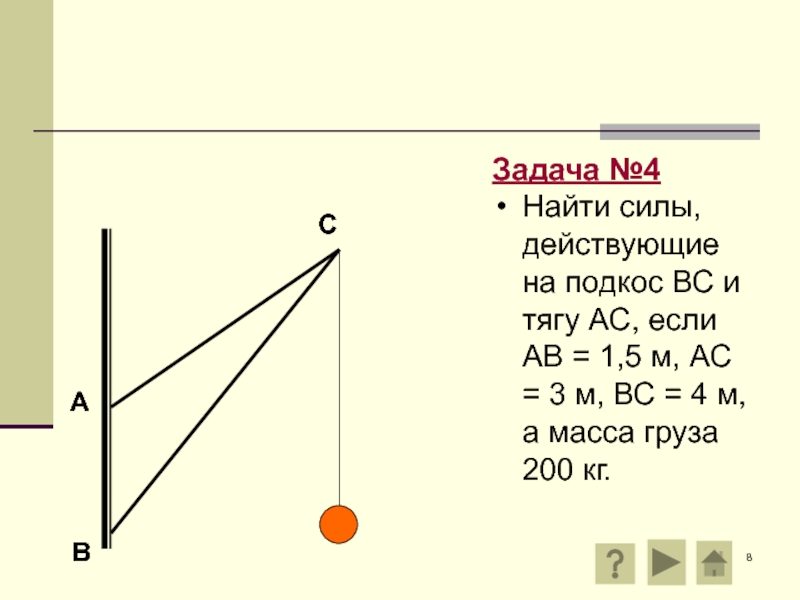
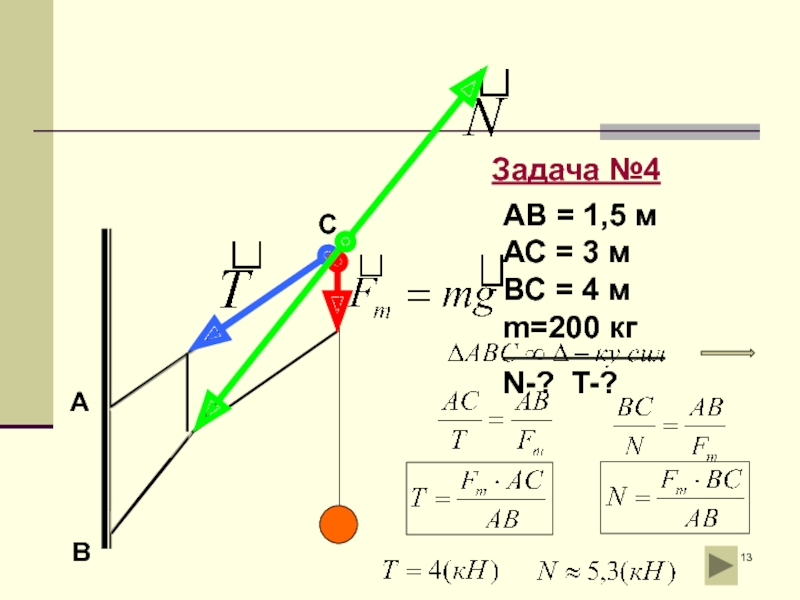
Задача №4
Найти силы, действующие на подкос ВС и тягу АС, если
А
В
С
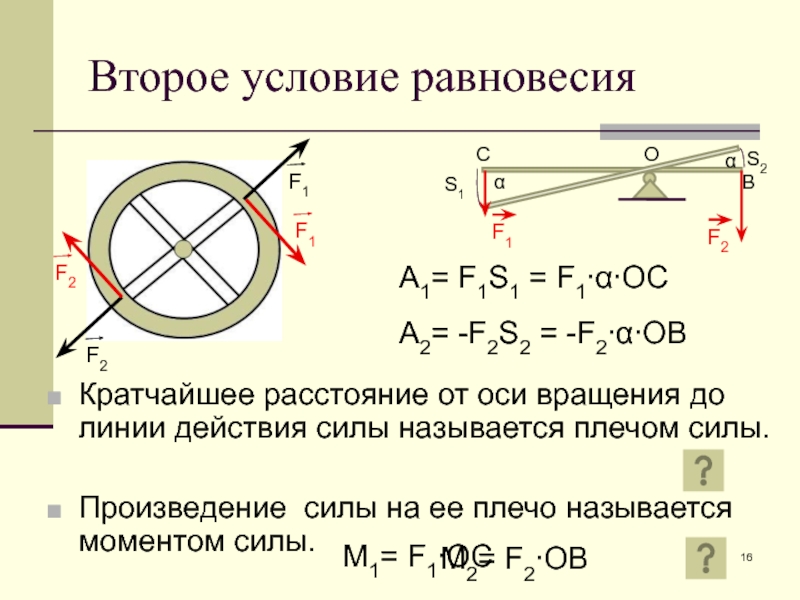
Слайд 16Второе условие равновесия
Кратчайшее расстояние от оси вращения до линии действия силы
Произведение силы на ее плечо называется моментом силы.
α
α
S1
S2
О
С
В
A1= F1S1 = F1∙α∙OC
A2= -F2S2 = -F2∙α∙OB
M1= F1∙OC
M2= F2∙OB
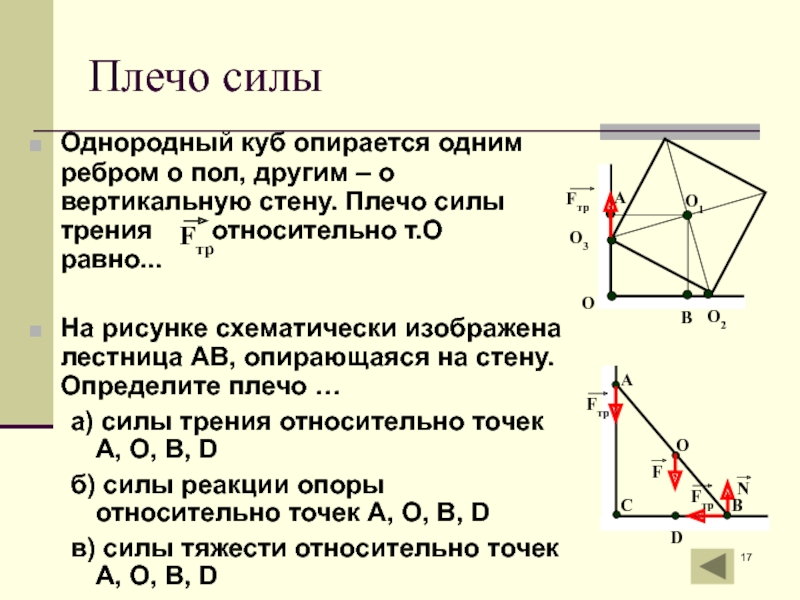
Слайд 17Плечо силы
Однородный куб опирается одним ребром о пол, другим – о
На рисунке схематически изображена лестница АВ, опирающаяся на стену. Определите плечо …
а) силы трения относительно точек А, О, В, D
б) силы реакции опоры относительно точек А, О, В, D
в) силы тяжести относительно точек А, О, В, D
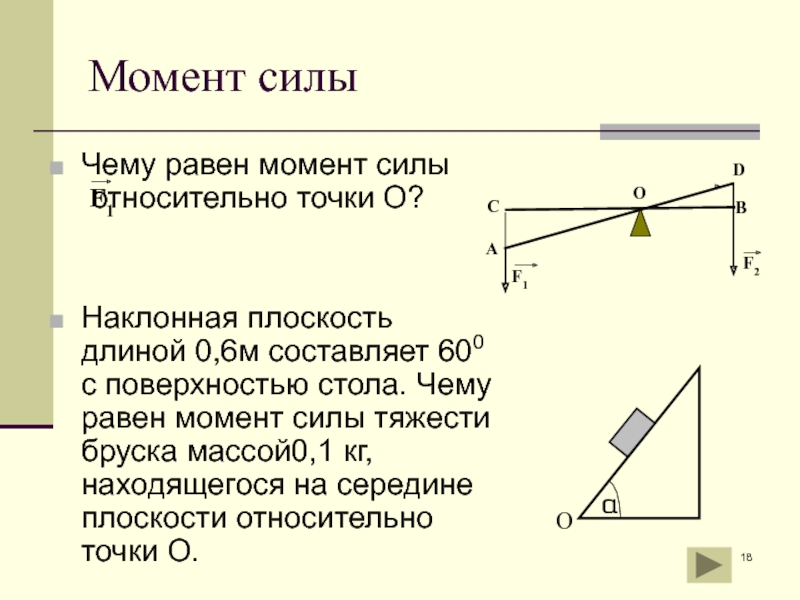
Слайд 18Момент силы
Чему равен момент силы
Наклонная плоскость длиной 0,6м составляет 600 с поверхностью стола. Чему равен момент силы тяжести бруска массой0,1 кг, находящегося на середине плоскости относительно точки О.
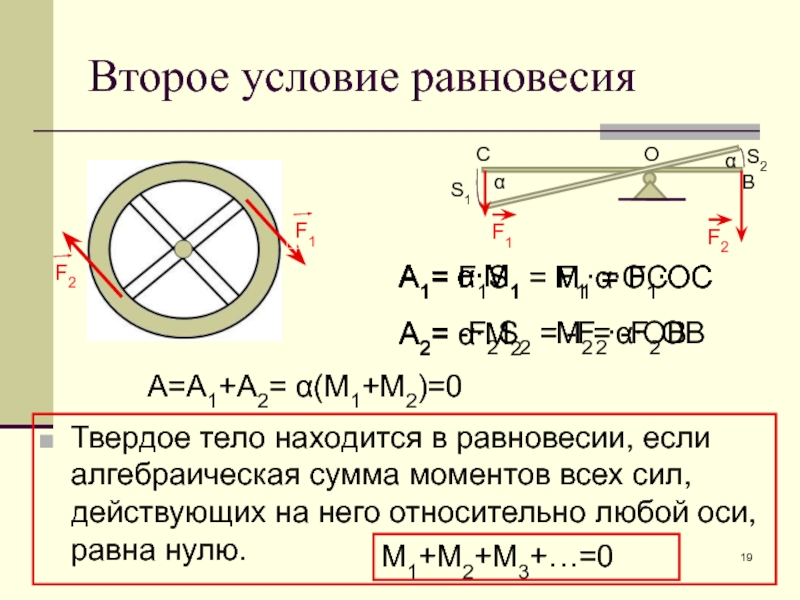
Слайд 19Второе условие равновесия
Твердое тело находится в равновесии, если алгебраическая сумма моментов
α
α
S1
S2
О
С
В
A1= F1S1 = F1∙α∙OC
A2= -F2S2 = -F2∙α∙OB
A1= α∙М1
М1 = F1∙OC
A2= α∙М2
М2= -F2ОВ
А=A1+А2= α(М1+М2)=0
М1+М2+М3+…=0
A1= α∙М1
М1 = F1∙OC
A1= α∙М1
Слайд 20Условия равновесия
Твердое тело находится в равновесии, если геометрическая сумма всех сил,
Твердое тело находится в равновесии, если алгебраическая сумма моментов всех сил, действующих на него относительно любой оси, равна нулю.
М1+М2+М3+…=0
1
2
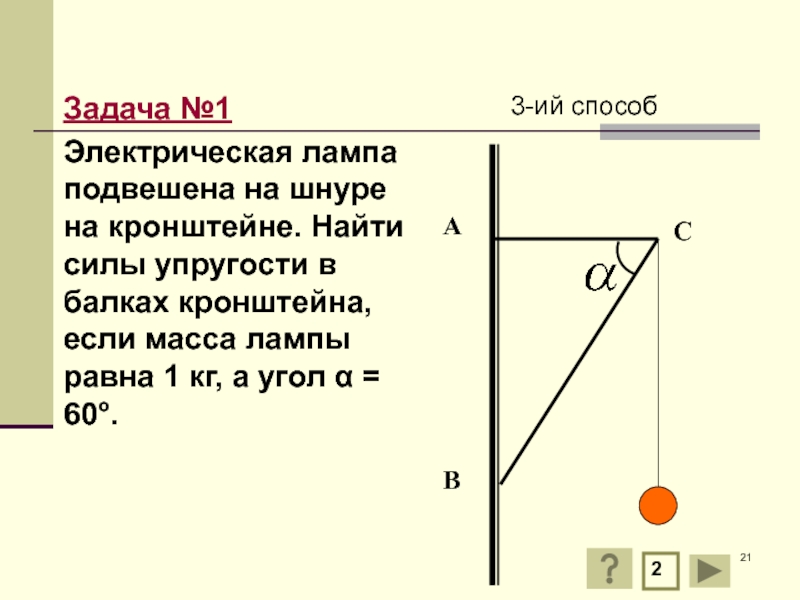
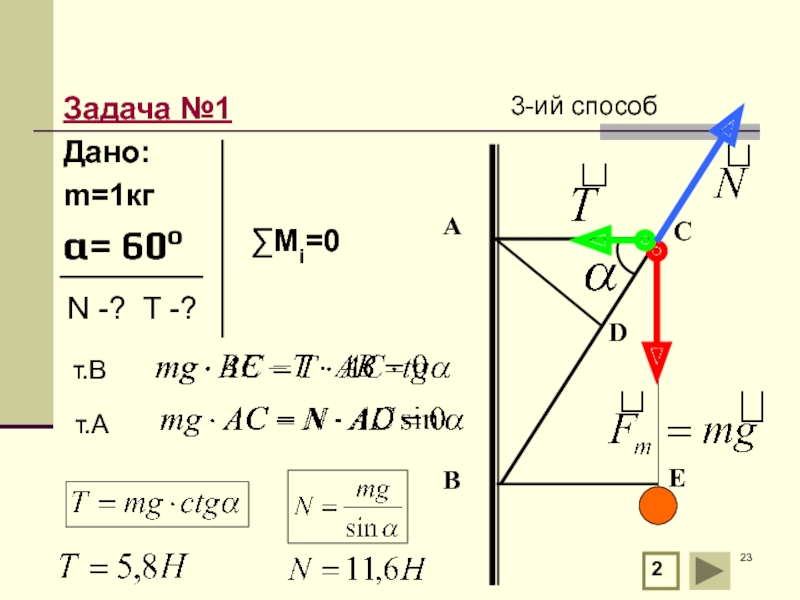
Слайд 21Задача №1
Электрическая лампа подвешена на шнуре на кронштейне. Найти силы упругости
А
В
С
3-ий способ
2
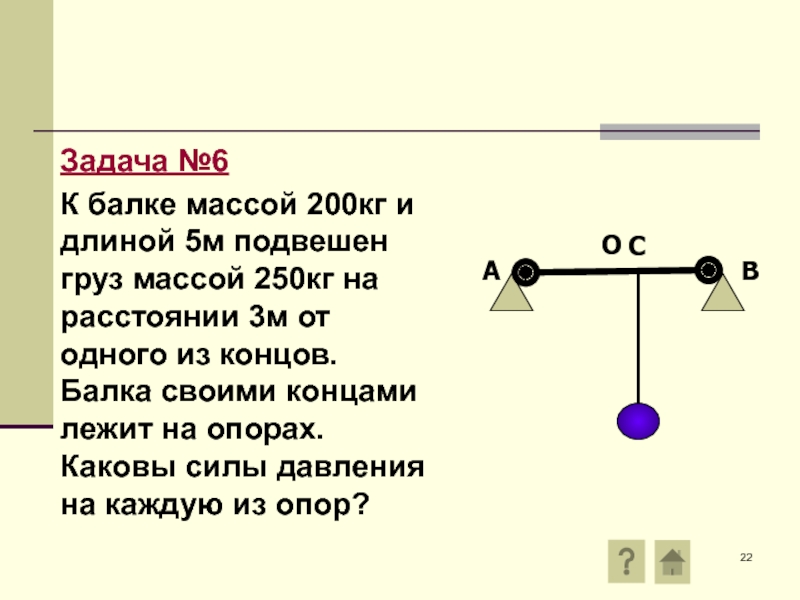
Слайд 22Задача №6
К балке массой 200кг и длиной 5м подвешен груз массой
O
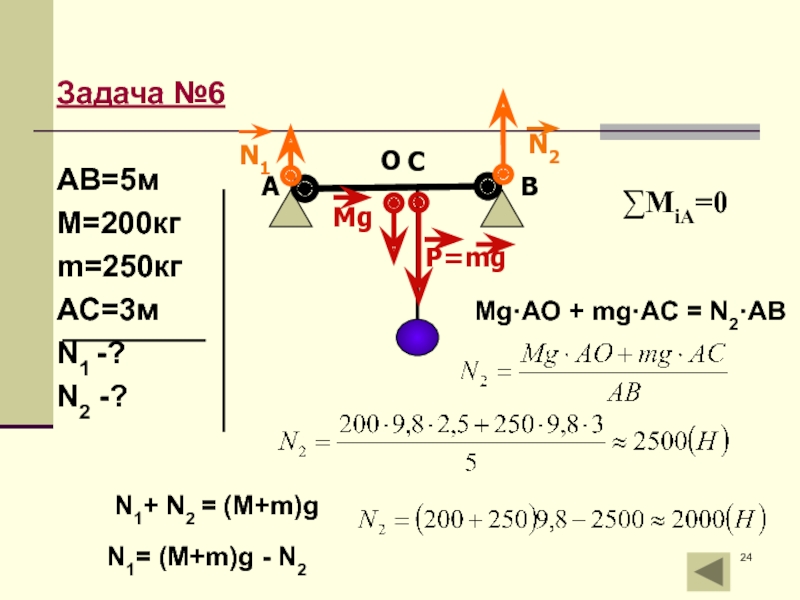
Слайд 24Задача №6
АВ=5м
М=200кг
m=250кг
АС=3м
N1 -?
N2 -?
∑МiA=0
O
Mg·AO + mg·AC = N2·AB
N1+ N2 =
N1= (M+m)g - N2
Слайд 26Что такое равновесие?
При каком условии твердое тело будет находиться в состоянии
При каком условии твердое тело способное вращаться будет находиться в состоянии равновесия?
Слайд 29Условия устойчивости равновесия
Тела находятся в состоянии устойчивого равновесия, если при малейшем
Тела находятся в состоянии неустойчивого равновесия, если при малейшем отклонении от положения равновесия возникает сила или момент силы, удаляющие тело от положения равновесия.
Тела находятся в состоянии безразличного равновесия, если при малейшем отклонении от положения равновесия не возникает ни сила, ни момент силы, изменяющие положение тела.
Слайд 31
Равновесие тел на опорах
Тело, имеющее площадь опоры, будет находиться в равновесии
Слайд 35На столе лежат три книги. Значения сил тяжести, действующих на каждую
1) 0
2) 12 Н
3) 5 Н
4) 9 Н
Слайд 36Однородный куб опирается одним ребром на пол, другим – на вертикальную стену. Плечо
2)
О2О1
3)
О1О
4)
О2О
1) 0
Слайд 37 Труба массой М = 1 т лежит на земле.
1) 10 кН
3) 15 кН 4) 20 кН
2) 5 кН
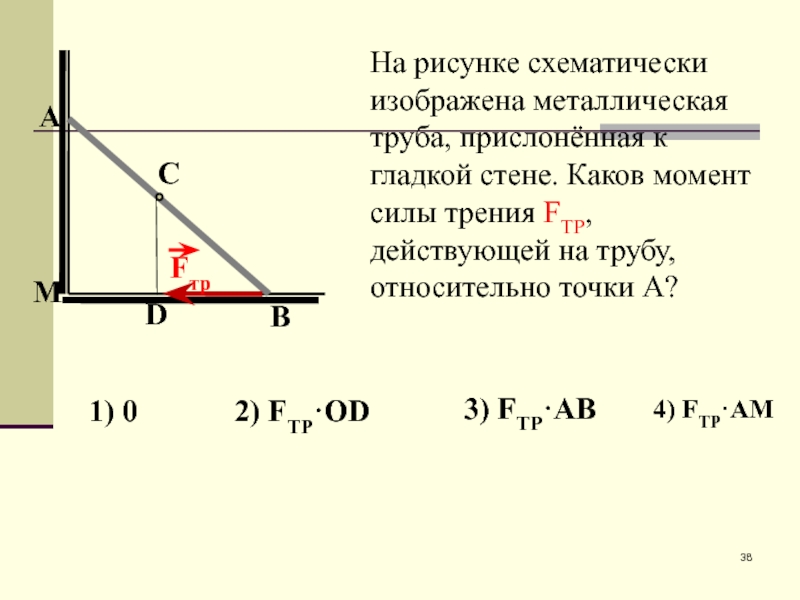
Слайд 38На рисунке схематически изображена металлическая труба, прислонённая к гладкой стене. Каков
1) 0
2) FТР·OD
3) FТР·AB
4) FТР·AM
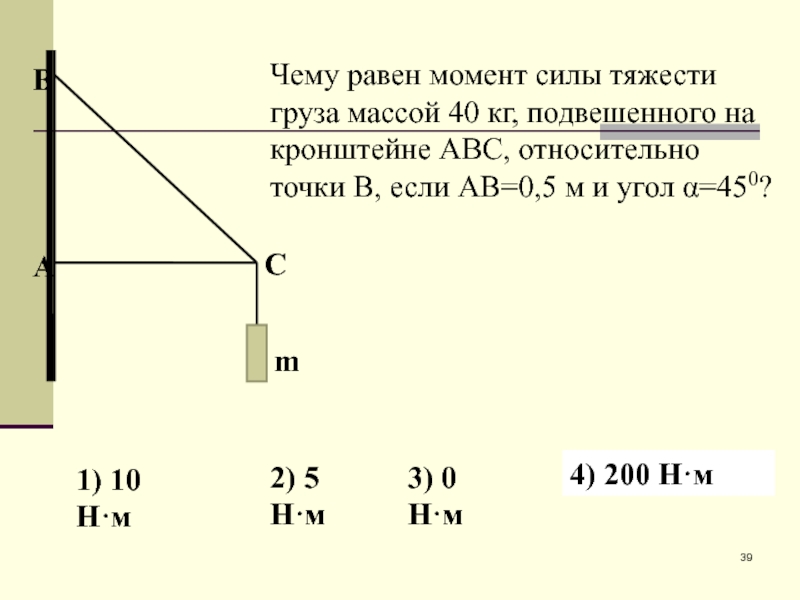
Слайд 39Чему равен момент силы тяжести груза массой 40 кг, подвешенного на
1) 10 Н·м
2) 5 Н·м
3) 0 Н·м
4) 200 Н·м
Слайд 40
При решении задач на равновесие тел:
Сделать рисунок, показать все силы, действующие
2. Для тела, не имеющего оси вращения, записать первое условие равновесия в векторной форме ∑F = 0, затем записать это условие равновесия в проекциях на оси координат и получить уравнение в скалярной форме.
3. Для тела, с закрепленной осью вращения, следует определить плечи всех сил относительно этой оси и использовать второе условие равновесия (правило моментов): ∑М = 0.Если из условия задачи следует, что ось вращения тела не закреплена, то необходимо использовать оба условия равновесия. При этом положение оси вращения следует выбирать так, чтобы через нее проходило наибольшее число линий действия неизвестных сил.
4. Решить полученную систему уравнений и определить искомые величины.
Слайд 41К гвоздю, вбитому в стенку, привязана нить, намотанная на катушку. Катушка
Задача №1
α
решение
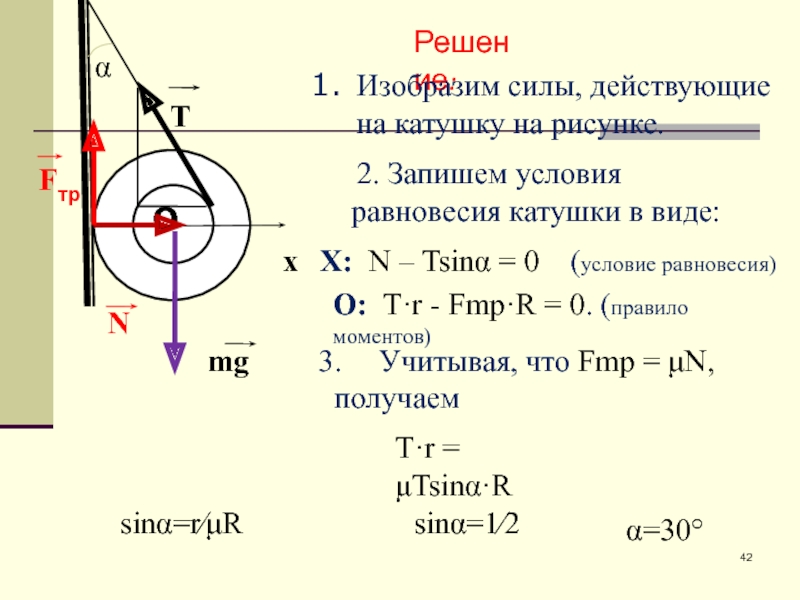
Слайд 42Решение:
Изобразим силы, действующие на катушку на рисунке.
mg
N
Fтр
T
2. Запишем условия равновесия
x
X: N – Tsinα = 0 (условие равновесия)
α
О: T·r - Fmp·R = 0. (правило моментов)
Учитывая, что Fmp = μN,
получаем
T·r = μTsinα·R
sinα=1⁄2
α=30°
sinα=r⁄μR
Слайд 43Цилиндр массой m = 150 кг удерживается на наклонной плоскости с
Задача №2
α
A
R
решение
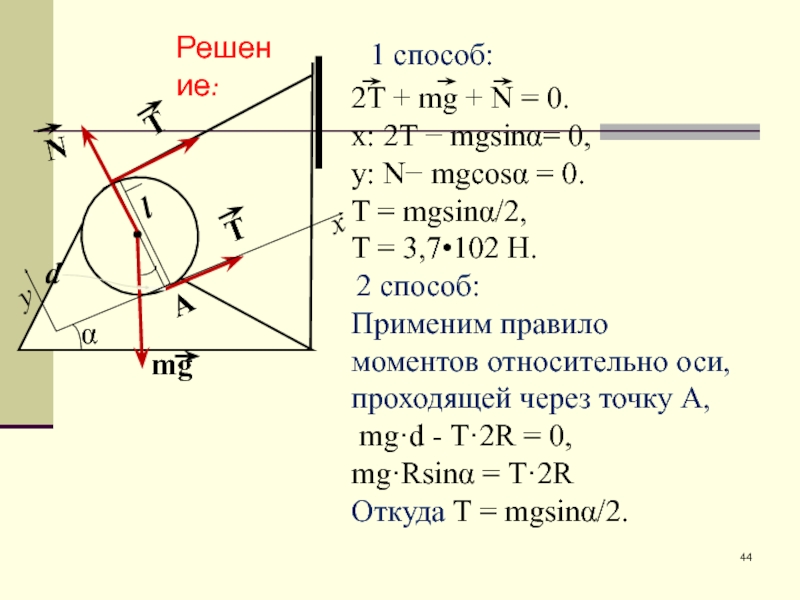
Слайд 44
2T + mg + N = 0.
x: 2T − mgsinα= 0,
y:
T = mgsinα/2,
T = 3,7•102 H.
x
y
1 способ:
2 способ:
Применим правило моментов относительно оси, проходящей через точку A,
mg·d - T·2R = 0,
mg·Rsinα = T·2R
Откуда T = mgsinα/2.
Решение:
Слайд 45Задача №3 Однородный шар радиуса R подвешен на нити длиной ℓ, конец
решение
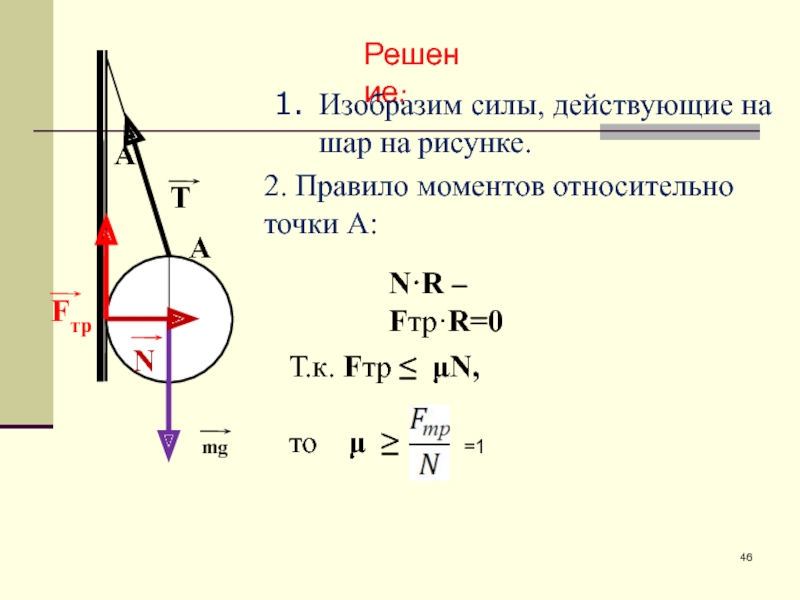
Слайд 46mg
N
Fтр
T
Α
Решение:
А
2. Правило моментов относительно
точки А:
N·R – Fтр·R=0
Изобразим силы, действующие
=1
Слайд 47Задача №4.
Какой минимальной горизонтальной силой можно опрокинуть через ребро куб, лежащий
F
решение
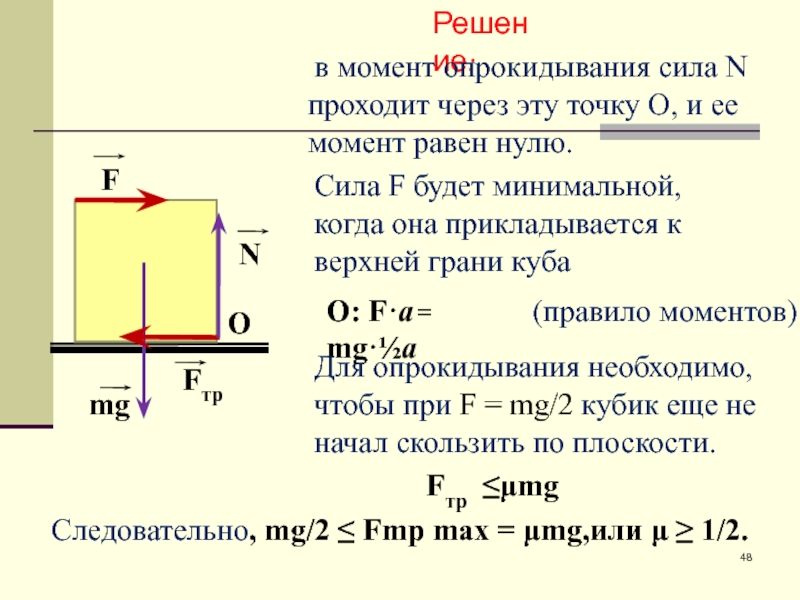
Слайд 48F
O
mg
Fтр
N
Решение:
в момент опрокидывания сила N проходит через эту точку О,
Сила F будет минимальной, когда она прикладывается к верхней грани куба
О: F·a= mg·½а
Для опрокидывания необходимо, чтобы при F = mg/2 кубик еще не начал скользить по плоскости.
Следовательно, mg/2 ≤ Fmp max = μmg,или μ ≥ 1/2.
(правило моментов)
Слайд 49Тонкостенная полусфера массой M и радиусом R покоится на горизонтальном столе.
решение
Задача №5.
Слайд 50
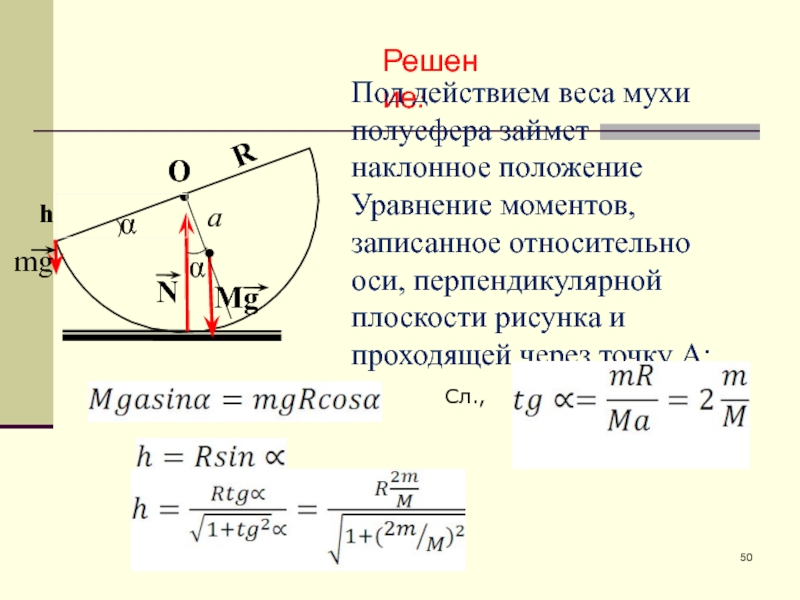
Решение:
Под действием веса мухи полусфера займет наклонное положение
Уравнение моментов, записанное
Сл.,