Синусоїдальний струм презентация

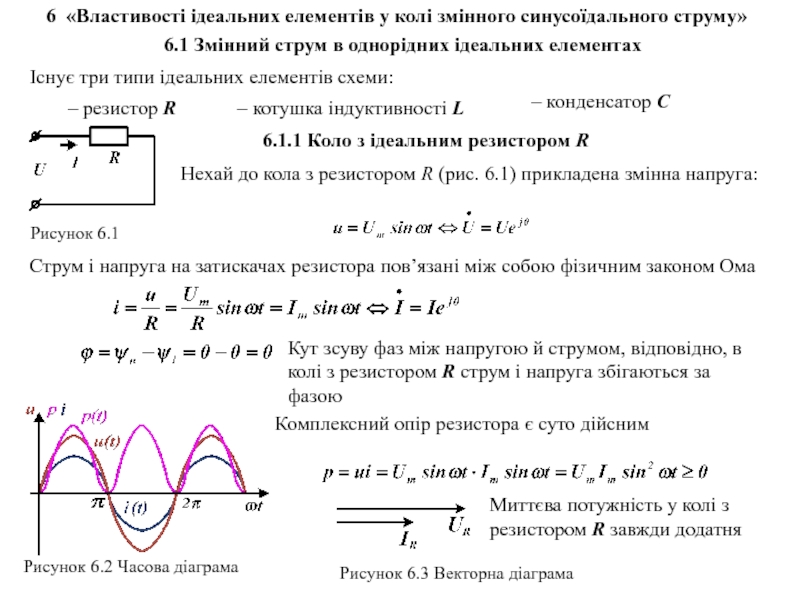
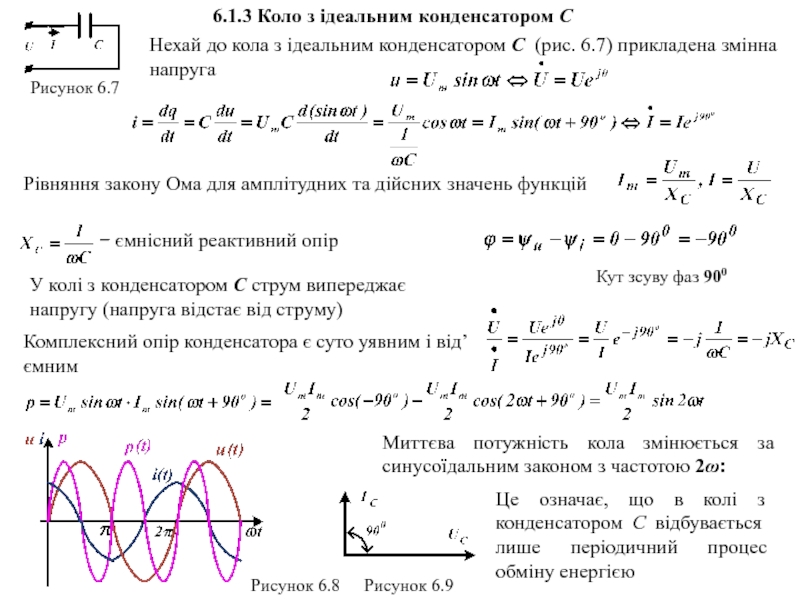
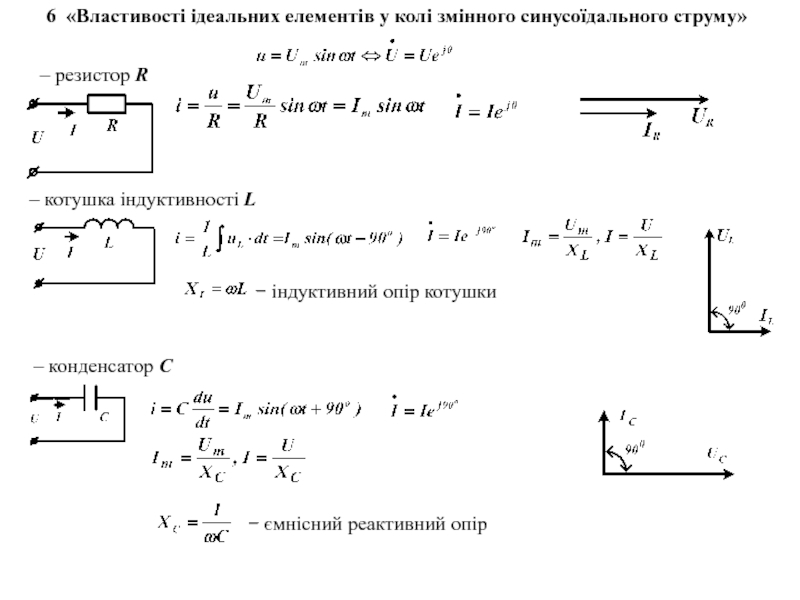
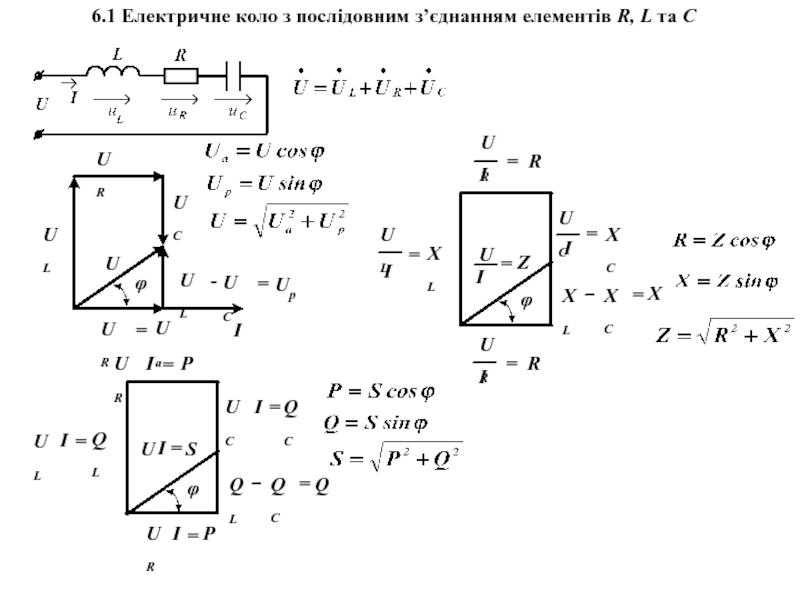
i(t)=Im sin(ωt+ψi ),

u(t)=Umsin(ωt+ψu)

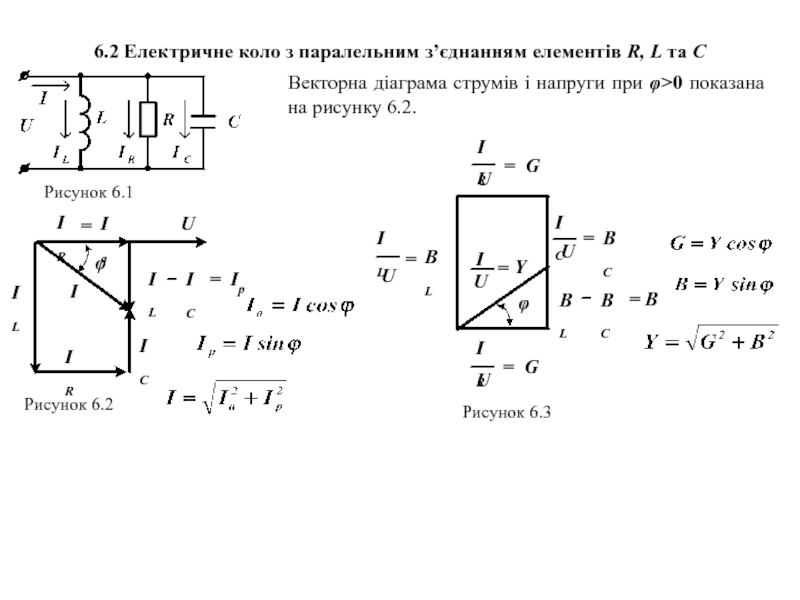
Рисунок 5.1

Т – називається періодом

– частота.

[с-1] або [рад/с] – кутова частота

u(t), i(t) або u, i − миттєві значення функцій, тобто їх значення в довільно обраний момент часу

Um, Im − амплітудні (максимальні) значення функцій

(ωt+ψ) − фаза, що визначається в момент часу

ψu, ψi – початкові фази функцій, що визначають їх значення в момент t=0, залежать від вибору початку відліку часу

ϕ = ψu−ψi – кут зсуву фаз (різниця початкових фаз) між напругою і струмом, не залежить від вибору початку відліку часу

5 Синусоїдальний струм

Основні поняття

5.1 Змінний струм (напруга) і характеризують його величини

Для змінного синусоїдального струму (напруги) середнє значення визначають за половину періоду (Т/2) між двома нульовими значеннями

Діючі значення змінного струму (напруги) визначається як середньоквадратичне значення функції за період

В електроенергетиці прийнято всі теоретичні розрахунки та експериментальні вимірювання виконувати для діючих значень струмів і напруг.

коефіцієнт амплітуди

коефіцієнт форми

а) довжина вектора в масштабі дорівнює амплітуді функції Im;

б) початкове положення вектора при t = 0 визначається початковою фазою Ψ

в) вектор рівномірно обертається з кутовою швидкістю ω, рівний кутовий частоті функції

Рисунок 5.2

Нехай задані два струми, записані у вигляді синусоїдальних функцій

Знайдемо їх суму у вигляді векторної діаграми (рис. 5.3)

Рисунок 5.3

1) алгебраїчній

2) тригонометричній

3) показниковій

j – уявне одиничне число

I – модуль комплексного числа

Ψ − аргумент комплексного числа

Ia – дійсна частина комплексного числа

Ip – уявна частина комплексного числа

Наведемо чисельні співвідношення, які найбільш часто зустрічаються

Зобразимо вектор струму на комплексній площині

Припустимо, що задані два числа, які записані в алгебраїчній і показниковій формах.

Додавання (віднімання) комплексних чисел проводиться в алгебраїчній формі

Множення (ділення) комплексних чисел може виконуватися

в алгебраїчній формі

в показниковій формі

Піднесення до степеня (добування кореня) комплексного числа виконується тільки в показниковій формі

Існує три типи ідеальних елементів схеми:

– резистор R

– котушка індуктивності L

– конденсатор C

6.1.1 Коло з ідеальним резистором R

Рисунок 6.1

Нехай до кола з резистором R (рис. 6.1) прикладена змінна напруга:

Струм і напруга на затискачах резистора пов’язані між собою фізичним законом Ома

Кут зсуву фаз між напругою й струмом, відповідно, в колі з резистором R струм і напруга збігаються за фазою

Комплексний опір резистора є суто дійсним

Миттєва потужність у колі з резистором R завжди додатня

Рисунок 6.2 Часова діаграма

Рисунок 6.3 Векторна діаграма

Струм та напруга на затискачах котушки пов’язані між собою законом електромагнітної індукції

Рівняння закону Ома для амплітудних та дійсних значень функцій

− індуктивний реактивний опір котушки

кут зсуву фаз 900 .

У колі з котушкою L струм відстає від напруги (напруга випереджає струм)

Комплексний опір котушки є суто уявним і додатнім

Миттєва потужність кола змінюється за синусоїдальним законом з частотою 2ω:

Це означає, що в колі з котушкою L відбувається лише періодичний процес обміну енергією .

Рисунок 6.5

Рисунок 6.6

− ємнісний реактивний опір

Рівняння закону Ома для амплітудних та дійсних значень функцій

Кут зсуву фаз 900

У колі з конденсатором С струм випереджає напругу (напруга відстає від струму)

Комплексний опір конденсатора є суто уявним і від’ємним

Миттєва потужність кола змінюється за синусоїдальним законом з частотою 2ω:

Це означає, що в колі з конденсатором С відбувається лише періодичний процес обміну енергією

Рисунок 6.8

Рисунок 6.9

– конденсатор C

− індуктивний опір котушки

− ємнісний реактивний опір

S

QC

Q

UR

I

=

P

6.1 Електричне коло з послідовним з’єднанням елементів R, L та C

Нехай у заданій схемі з послідовним з’єднанням елементів R, L та C (рис. 6.10) протікає змінний струм

рівняння в комплексній формі

где

− комплексний опір,

− реактивний опір

− модуль комплексного опору або повний опір

− аргумент комплексного опору або кут зсуву фаз між напругою та струмом на вході схеми

При φ>0, при цьому коло має активно-індуктивний характер

при φ<0 – коло має активно-ємнісний характер.

Рівняння закону Ома для послідовної схеми матиме вигляд

− в комплексній формі,

− в звичайній формі для модулів

Векторна діаграма струмів і напруги при φ>0 показана на рисунку 6.2.

Рисунок 6.2

U

Ip

φ

IR

IL

IC

=

IR

=

Ia

IL

IC

I

I

φ

IR

IL

IC

=

BL

U

=

BL

U

=

G

U

=

BC

=

U

Y

BC

B

IR

U

=

G

Рисунок 6.3

I1=3 A, I2=4 A, I3=4 A, I4=3 A.

За заданим показаннями амперметрів знайти значення струмів I5, I, I6.

рівняння в комплексній формі

− комплексна провідність

− активна провідність

− індуктивна провідність

− ємнісна провідність

− реактивна (еквівалентна) провідність

− модуль комплексної провідності або повна провідність

− аргумент комплексної провідності або кут зсуву фаз між напругою та струмом на вході схеми

При (ВL–BC) >0 и φ>0 – коло в цілому має активно-індуктивний характер

при (ВL–BC) <0 и φ<0 – коло в цілому має активно-ємнісний характер

Для послідовної схеми (рис. 7.1) справедливі співвідношення

Для паралельної схеми (рис. 7.2) справедливі співвідношення

Порівнюючи праві частини рівнянь отримаємо співвідношення між параметрами еквівалентних схем

7 «Еквівалентні перетворення електричних кіл змінного струму»

активної складової Uа, яка збігається з вектором струму I,

й реактивної складової Uр, перпендикулярної до вектора струму (рис. 7.3).

Рисунок 7.4

Якщо сторони трикутника напруг поділити на струм I, то отримаємо новий трикутник опорів, подібний вихідному, гіпотенузою

якого є повний опір,

катетами – активний опір R

і реактивний опір X.

З трикутника опорів (рис. 7.4) слідують співвідношення:

Паралельній схемі заміщення (рис. 7.2) відповідає представлення вектора струму у вигляді суми двох складових:

активної складової Iа, яка збігається з вектором напруги U,

й реактивної складової Iр, перпендикулярної до вектора U (рис. 7.5).

Рисунок 7.5

З отриманого трикутника струмів (рис. 7.5) слідують співвідношення:

Рисунок 7.6

Y – повна провідність

G – активна провідність

B - реактивна провідність

Якщо сторони трикутника струмів (рис 7.5) поділити на напругу U, то отримаємо новий трикутник провідностей (рис. 7.6), подібний вихідному.

Символічний метод обчислення кіл синусоїдального струму заснований на законах Кірхгофа та законі Ома в комплексній формі

Рівняння, що виражають закони Кірхгофа в комплексній формі, мають цілком такий же вигляд, як і відповідні рівняння для кіл постійного струму.

Перший закон Кірхгофа в комплексній формі:

Другий закон Кірхгофа в комплексній формі:

Розглянемо застосування законів Кірхгофа для розгалуженого електричного кола (рис. 8.1),

параметри:

X3=50 Oм.

U=120 B

X1=100 Oм

R1= 25 Oм

X2=50 Oм

R2= 20 Oм

Визначити струми у гілках електричного кола.

Скласти рівняння балансу потужності

Розв’язання

1 Запишемо вираз для визначення еквівалентного опору кола:

2 Приймемо початкову фазу джерела за нуль, запишемо:

3 Визначимо перший струм за законом Ома:

Символічний метод обчислення кіл синусоїдального струму заснований на законах Кірхгофа та законі Ома в комплексній формі

Рівняння, що виражають закони Кірхгофа в комплексній формі, мають цілком такий же вигляд, як і відповідні рівняння для кіл постійного струму.

Перший закон Кірхгофа в комплексній формі:

Другий закон Кірхгофа в комплексній формі:

Розглянемо застосування законів Кірхгофа для розгалуженого електричного кола (рис. 8.1),

параметри:

X3=50 Oм.

U=120 B

X1=100 Oм

R1= 25 Oм

X2=50 Oм

R2= 20 Oм

Визначити струми у гілках електричного кола.

Скласти рівняння балансу потужності

Розв’язання

1 Запишемо вираз для визначення еквівалентного опору кола:

6 Складаємо рівняння балансу потужності

2 Приймемо початкову фазу джерела за нуль, запишемо:

3 Визначимо перший струм за законом Ома:

6 Складаємо рівняння балансу потужності

2 Приймемо початкову фазу джерела за нуль, запишемо:

3 Визначимо перший струм за законом Ома:

та електричним полем конденсатора

Умова для резонансного режиму через параметри елементів схеми:

В резонансному режимі коливання енергії між магнітними й електричними полями замикаються всередині кола

Обмін енергією між джерелом та колом відсутній

Електричне коло по відношенню до джерела енергії веде себе як суто активний опір R (активна провідність G).

схеми з боку виводів джерела енергії повинні мати чисто активний характер

- вхідний опір Zвх=Rвх

- вхідна провідність Yвх=Gвх

Умова резонансу напруг:

Xэ= XL − XC =0

або

− резонансна або власна частота.

З отриманої рівності слідує, що резонансного режиму в колі можна досягти зміною параметрів елементів L та C або частоти джерела ω.

В резонансному режимі повний опір схеми має мінімальне значення й рівне активному опору:

Струм максимальний і збігається за фазою з напругою джерела: I=U/R; ϕ = 0.

Напруга на резисторі рівна напрузі джерела: UR=IR=U.

Напруга на реактивних елементах рівні за модулем, протилежні за фазою й взаємно компенсують один одного:

Напруги на реактивних елементах

можуть значно перевищувати напругу джерела U за умови, що XL=XC>>R.

Властивості такого кола як коливального контуру характеризують наступні параметри:

− хвильовий опір,

− добротність контура.

900

UL

U

UС

-900

I

U

I

Резонансні характеристики

Резонансними характеристиками називаються залежності режимних параметрів від частоти: UL, UC, I, ϕ = f(ω)

XC

Z

R

X

XC

XL

XL

=

-

Частотні характеристики

Частотними характеристиками контура називаються залежності опорів окремих елементів та ділянок від частоти XL (ω), XC (ω), Z(ω), XC (ω)

Умова резонансу струмів:

− резонансна (власна) частота.

В резонансному режимі повна провідність схеми рівна активній провідності й має мінімальне значення:

Струм джерела також мінімальний й збігається за фазою з напругою джерела (ϕ = 0):
I =UY = Ug.

Струми в гілках з реактивними елементами

IL= − UbL,

IC =UbC

протилежні за фазою й компенсують один одного

рівні за модулем,

Струм в резисторі R рівний струму джерела (I=IR=Ug).

За умови, що bL=bC>>g

струми в реактивних елементах IL = IC

можуть значно перевищувати струм джерела I

Електричне коло з паралельним з’єднанням елементів R, L та C в техніці отримало назву паралельного коливального кола.

− хвильова провідність;

− добротність контура.

I

IR

IL

IC

=

-bL

bC

b

bC

bL

Частотні характеристики провідностей окремих елементів

Резонансні характеристики паралельного контура

IL (ω), IC (ω), IR (ω), I (ω)

bL (ω), bC (ω), b (ω)

b

I

U

I1

I2

R1

X1

R2

Так як гілки з реактивними елементами з’єднанні паралельно, то в колі може виникнути резонанс струмів.

Вхідна комплексна провідність схеми:

Запишемо умову резонансу

Запишемо вираз для визначення активних та реактивних складових струмів у гілках:

I1р

U

I2а

I2р

I2

I1

I1а

I2а

I1а

I

Ф12

Якщо магнітне поле, яке створюється однією з котушок, перетинає площину витків (зчеплене з витками) другої котушки, то такі котушки прийнято називати індуктивно зв’язаними

Ф11 — частина магнітного потоку, яке створюється струмом i1, який зчеплений лише з витками котушки w1.

Ф22 — частина магнітного потоку, яке створюється струмом i2, який зчеплений лише з витками котушки w2.

Ф12 — частина магнітного потоку, який створюється струмом i1, який зчеплений з витками обох котушок (взаємний потік).

Ф21 — частина магнітного потоку, який створюється струмом i2, який зчеплений з витками обох котушок (взаємний потік).

Ф1 = Ф11 + Ф12 — сумарний магнітний потік, який створюється струмом i1.

Ф2 = Ф22 + Ф21 — сумарний магнітний потік, який створюється струмом i2.

Власною індуктивністю котушки L називається відношення її власного потокозчеплення струму в ній:

Взаємною індуктивністю М називається відношення взаємного потокозчеплення 2-ї котушки до струму в 1-й або навпаки:

Ступінь магнітного зв’язку між котушками характеризується коефіцієнтом зв’язку:

При протіканні одночасно за обома котушкам постійних струмів i1 та i2 їх власні й взаємні магнітні потоки можуть збігатися за напрямком (співнапрямленні), й тоді виникає посилення магнітного поля, або можуть не збігатися (протилежно напрямленні), тоді виникає послаблення маг­нітного поля.

Якщо при обраних напрямках струмів в котушках їх власні й взаємні потоки збігаються, то такі напрямки струмів прийнято називати співнапрямленними (в протилежному випадку − зустрічними).

На схемах електричних кіл однойменні виводи котушок позначаються однаковими символьними знаками (зірочка, точка), а наявність взаємного магнітного зв’язку − дугою зі стрілками на кінцях

При протіканні по котушкам змінних синусоїдальних струмів у них за законом електромагнітної індукції будуть наводитися одночасно ЕРС самоіндукції та ЕРС взаємної індукції, які в сумі врівноважать прикладені до котушок напруги:

− диференціальна форма рівнянь 2-го закону Кірхгофа

− комплексна форма рівнянь 2-го закону Кірхгофа

- індуктивні опори котушок індуктивності,

- опір взаємоіндукції.

При співнапрямленному включенні власні й взаємні магнітні потоки будуть складуватися, а при зустрічному — відніматись.

За другим законом Кірхгофа:

− диференціальна форма,

− комплексна форма

I

IXМ

IX1

IX2

IR1

IR2

U1

U2

U

IXМ

I

IXМ

IX1

IX2

IR1

IR2

U1

U2

U

IXМ

З комплексного рівняння слідує:

Розв’язуючи разом останні рівняння, отримаємо:

Дві котушки з опорами R1 та R2, індуктивностями L1 та L2 й взаємною індуктивністю М з’єднанні паралельно, причому однойменні виводи приєднанні до одного й того ж вузла

Для обраних додатних напрямків струмів за законами Кірхгофа запишемо наступні вирази:

У цих рівняннях комплексні напруги

так як додатні напрямки струмів у гілках відносно однойменних виводів однакові.

взяті зі знаком плюс,

Розв’язав рівняння, отримаємо вхідний опір кола

Тут струми й однаково орієнтовані відносно однойменних затискачів, тому включення котушок узгоджене.

Запишемо вирази

Перетворимо рівняння для напруг між виводами 1–3 й 2–3:

додамо доданок

додамо доданок

Після перетворень отримаємо наступні вирази:

Підставимо третій струм у рівняння для напруг:

Зобразимо схему, відповідно перетвореним рівнянням.

L1

L2

L3

М13

М12

М23

L1

L2

L3

М13

М23

+М12

+М12

-М12

L2

L3

+М12

+М12

-М12

+М13

+М13

-М13

+М23

-М23

-М23

I1

I2

I3

M12

M23

e1

e2

X3

Запишемо систему рівнянь за законами Кірхгофа в диференціальній формі

Комплексна форма запису системи рівнянь:

Метод контурних струмів

e1

e2

С3

Метод контурних струмів

Обчислення опорів гілок:

e1

e2

С3

Метод двох вузлів

- комплексні провідності гілок

b

а

струми гілок

Потужність джерел

Потужність споживачів