Сергей Петрович
ауд. 246 м.к
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Синтез зубчатых передач презентация
Содержание
- 1. Синтез зубчатых передач
- 2. Основная теорема зацепления. Плоские ЗП с круглыми
- 3. Основная теорема зацепления. Пусть в данный момент
- 4. Основная теорема зацепления.
- 5. Основная теорема зацепления. Проекции скоростей VM1 и
- 6. Основная теорема зацепления. где α1 и α2
- 7. Основная теорема зацепления. Тогда: Или
- 8. Основная теорема зацепления. Окончательно получим: что
- 9. Эвольвента окружности. Эвольвентой окружности называется кривая, которую
- 10. Эвольвента окружности.
- 11. Основные свойства эвольвенты окружности. Нормаль к эвольвенте
- 12. Основные свойства эвольвенты окружности. Расстояние по нормали
- 13. Параметрические уравнения эвольвенты окружности в полярных координатах.
- 14. Параметрические уравнения эвольвенты окружности в полярных координатах.
- 15. Параметрические уравнения эвольвенты окружности в полярных координатах.
- 16. Параметрические уравнения эвольвенты окружности в полярных координатах.
- 17. Удовлетворение эвольвентных профилей зубьев следствию из основной
- 18. Удовлетворение эвольвентных профилей зубьев следствию из основной теоремы зацепления.
- 19. Удовлетворение эвольвентных профилей зубьев следствию из основной
- 20. Удовлетворение эвольвентных профилей зубьев следствию из основной
- 21. Удовлетворение эвольвентных профилей зубьев следствию из основной
- 22. Удовлетворение эвольвентных профилей зубьев следствию из основной
- 23. Удовлетворение эвольвентных профилей зубьев следствию из основной
- 24. Удовлетворение эвольвентных профилей зубьев следствию из основной
- 25. Удовлетворение эвольвентных профилей зубьев следствию из основной
- 26. Удовлетворение эвольвентных профилей зубьев следствию из основной
- 27. Зацепление зубчатого колеса с зубчатой рейкой. Пусть
- 28. Зацепление зубчатого колеса с зубчатой рейкой.
- 29. Зацепление зубчатого колеса с зубчатой рейкой. То
- 30. Зацепление зубчатого колеса с зубчатой рейкой. В
Слайд 1Теория механизмов и машин
Лекция 11
Синтез зубчатых передач.
Лектор: ассистент каф. 202
Светличный
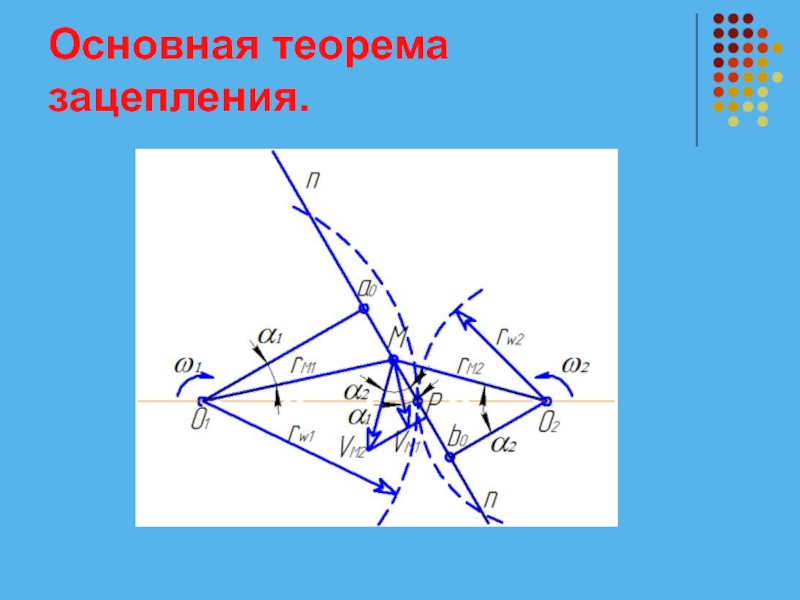
Слайд 2Основная теорема зацепления.
Плоские ЗП с круглыми зубьями обеспечивают вращательные движения с
постоянным передаточным отношениями. Это достигается выбором для профилей специальных кривых.
Геометрические условия, которым должны удовлетворять эти кривые, определяются основной теоремой зацепления: Общая нормаль к соприкасающимся (взаимо огибаемым) профилям зубьев делит линию осей колес на части, обратно пропорциональные угловым скоростям.
Геометрические условия, которым должны удовлетворять эти кривые, определяются основной теоремой зацепления: Общая нормаль к соприкасающимся (взаимо огибаемым) профилям зубьев делит линию осей колес на части, обратно пропорциональные угловым скоростям.
Слайд 3Основная теорема зацепления.
Пусть в данный момент времени в точке М соприкасаются
профили зубьев двух колес, вращающихся вокруг осей О1 и О2 с угловыми скоростями ω1 и ω2 .
Общая нормаль к профилям зубьев nn пересекает линию осей О1 О2 в точке р.
Скорость точки М в системе первого и второго колес:
Общая нормаль к профилям зубьев nn пересекает линию осей О1 О2 в точке р.
Скорость точки М в системе первого и второго колес:
Слайд 5Основная теорема зацепления.
Проекции скоростей VM1 и VM2 на общую нормаль n-n
должны быть равны, так как в противном случае зубья или внедряются друг в друга или разъединяются:
или
или
Слайд 6Основная теорема зацепления.
где α1 и α2 – углы, образованные векторами VM1
и VM2 с общей нормалью n-n.
Опустим из точек О1 и О2 перпендикуляры на общую нормаль n-n. Величины этих перпендикуляров соответственно равны:
Опустим из точек О1 и О2 перпендикуляры на общую нормаль n-n. Величины этих перпендикуляров соответственно равны:
Слайд 8Основная теорема зацепления.
Окончательно получим:
что и требовалось доказать.
Следствие: Для постоянства передаточного отношения
соприкасающиеся части профилей зубьев должны быть очерчены по таким кривым, чтобы в любой момент времени их контакта общая нормаль к ним проходила через одну и ту же точку р на линии осей, называемую полюсом зацепления.
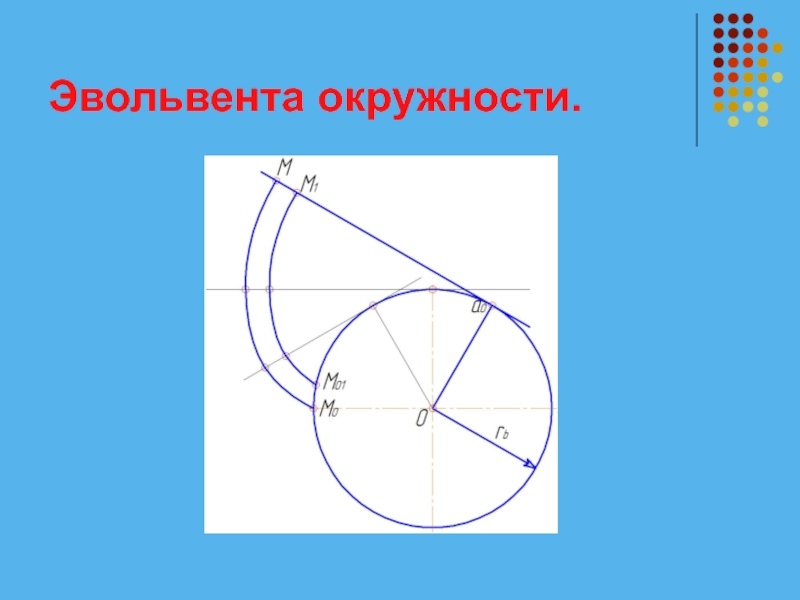
Слайд 9Эвольвента окружности.
Эвольвентой окружности называется кривая, которую описывает точка прямой линии, катящейся
по окружности без скольжения.
Окружность по которой перекатывается прямая, называется основной окружностью, а сама прямая – производящей прямой.
Основная окружность является эволютой, т.е. геометрическим местом центров кривизны эвольвенты.
Окружность по которой перекатывается прямая, называется основной окружностью, а сама прямая – производящей прямой.
Основная окружность является эволютой, т.е. геометрическим местом центров кривизны эвольвенты.
Слайд 11Основные свойства эвольвенты окружности.
Нормаль к эвольвенте в любой точке является касательной
к основной окружности (Ма0 – нормаль к эвольвенте в точке М).
Радиус кривизны эвольвенты в любой ее точке равен длине касательной к основной окружности, проведенной из этой точки (ρМ= Ма0).
Радиус кривизны эвольвенты в любой ее точке равен длине касательной к основной окружности, проведенной из этой точки (ρМ= Ма0).
Слайд 12Основные свойства эвольвенты окружности.
Расстояние по нормали между равноотстоящими (эквидистантными) эвольвентами равно
длине меньшей дуги основной окружности между точками возврата М0 и М01:
Эвольвента имеет две ветви, симметричные относительно прямой проходящей через центр окружности и точку возврата.
Эвольвента имеет две ветви, симметричные относительно прямой проходящей через центр окружности и точку возврата.
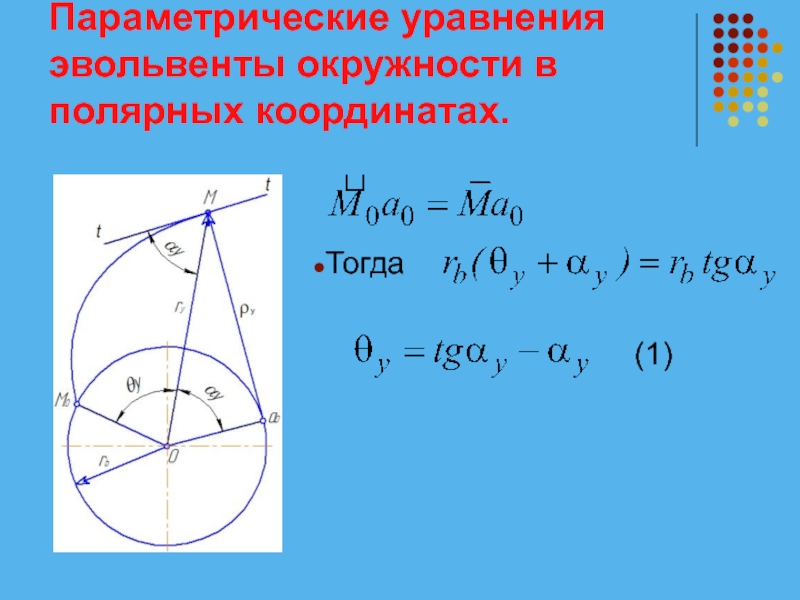
Слайд 13Параметрические уравнения эвольвенты окружности в полярных координатах.
Полярными координатами произвольной точки М
эвольвенты окружности являются эвольвентный угол θy и радиус-вектор ry.
Острый угол αy между касательной к эвольвенте в рассматриваемой точке и радиус-вектором этой точки называется углом профиля. Очевидно, что ∠МОа0 = αy.
Выражение для эвольвентного угла определяется из условия перекатывания производящей прямой по основной окружности:
Острый угол αy между касательной к эвольвенте в рассматриваемой точке и радиус-вектором этой точки называется углом профиля. Очевидно, что ∠МОа0 = αy.
Выражение для эвольвентного угла определяется из условия перекатывания производящей прямой по основной окружности:
Слайд 15Параметрические уравнения эвольвенты окружности в полярных координатах.
Тригонометрическая функция
называется эвольвентной функцией и сокращенно обозначается invαy (инвалюта αy ).
Выражение для радиуса-вектора находится из треугольника Оа0М:
Выражение для радиуса-вектора находится из треугольника Оа0М:
(2)
Слайд 16Параметрические уравнения эвольвенты окружности в полярных координатах.
Зависимости (1) и (2) представляют
собой уравнения эвольвенты в полярных координатах с параметром αy. Радиус кривизны эвольвенты равен:
(3)
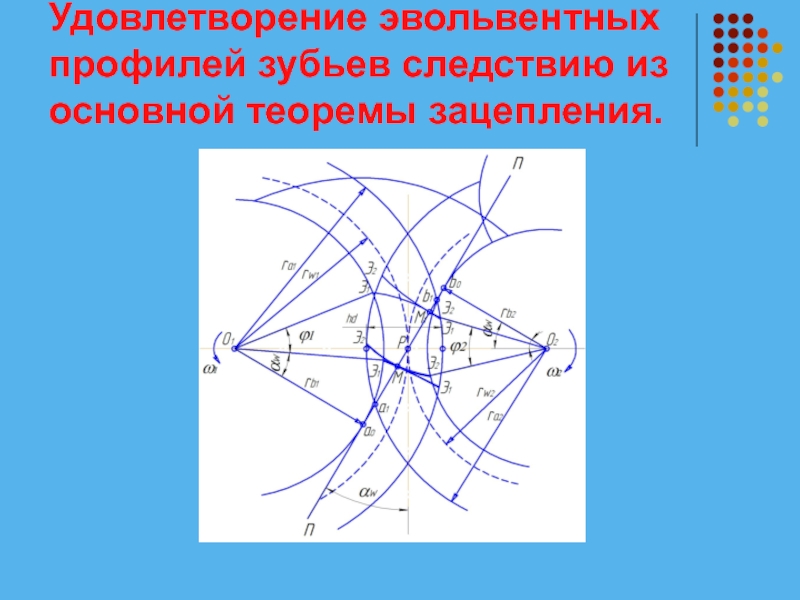
Слайд 17Удовлетворение эвольвентных профилей зубьев следствию из основной теоремы зацепления.
Докажем, что если
профили зубьев очерчены по эвольвентам окружностей, то передача вращения будет происходить с постоянным передаточным отношением, т.е будет удовлетворятся следствие из основной теоремы зацепления.
Пусть О1 и О2 – оси вращения зубчатых колес. Разделим линию О1О2 точкой р на части, обратно пропорциональные угловым
Пусть О1 и О2 – оси вращения зубчатых колес. Разделим линию О1О2 точкой р на части, обратно пропорциональные угловым
Слайд 19Удовлетворение эвольвентных профилей зубьев следствию из основной теоремы зацепления.
скоростям ω1 и
ω2. Радиусами rw1=O1p и rw2=O2p проведем начальные окружности.
Через точку р под произвольным углом к линии О1О2 проведем прямую n-n. Из точек О1 и О2 опустим перпендикуляры О1а0 и О2b0 на линию n-n и радиусами О1а0 и О2b0 опишем окружности. Эти окружности примем за основные окружности зубчатых колес (rb1= О1а0, rb2= О2b0), прямую n-n – за производящую прямую.
Через точку р под произвольным углом к линии О1О2 проведем прямую n-n. Из точек О1 и О2 опустим перпендикуляры О1а0 и О2b0 на линию n-n и радиусами О1а0 и О2b0 опишем окружности. Эти окружности примем за основные окружности зубчатых колес (rb1= О1а0, rb2= О2b0), прямую n-n – за производящую прямую.
Слайд 20Удовлетворение эвольвентных профилей зубьев следствию из основной теоремы зацепления.
Возьмем на прямой
n-n между точками а0 и b0 точку М.
При качении прямой n-n по основной окружности первого колеса точка М опишет эвольвенту Э1Э1, при качении прямой n-n по основной окружности второго колеса точка М опишет эвольвенту Э2Э2.
Примем эти эвольвенты за соприкасающиеся профили зубьев, ограничив их окружностями вершин радиусами ra1 и ra2.
При качении прямой n-n по основной окружности первого колеса точка М опишет эвольвенту Э1Э1, при качении прямой n-n по основной окружности второго колеса точка М опишет эвольвенту Э2Э2.
Примем эти эвольвенты за соприкасающиеся профили зубьев, ограничив их окружностями вершин радиусами ra1 и ra2.
Слайд 21Удовлетворение эвольвентных профилей зубьев следствию из основной теоремы зацепления.
В данный момент
времени эвольвенты Э1Э1 и Э2Э2 касаются в точке М и имеют общую нормаль а0Мb0, которая делит линию осей О1О2 на части обратно пропорциональные угловым скоростям, т.е:
Пусть за время t первое колесо повернулось на угол ϕ1, а второе колесо – на угол ϕ2.
Пусть за время t первое колесо повернулось на угол ϕ1, а второе колесо – на угол ϕ2.
Слайд 22Удовлетворение эвольвентных профилей зубьев следствию из основной теоремы зацепления.
Профили в колес
в новом положении имеют контакт в точке М1, которая будет также находится на линии n-n, так как в противном случае соприкасающиеся эвольвенты не имели бы общей нормали в точке касания.
Но если точка М1 лежит на прямой , являющейся общей нормалью к эвольвентным профилям зубьев в их новом положении, то, следовательно, для нового положения сохраняется прежнее передаточное отношение.
Но если точка М1 лежит на прямой , являющейся общей нормалью к эвольвентным профилям зубьев в их новом положении, то, следовательно, для нового положения сохраняется прежнее передаточное отношение.
Слайд 23Удовлетворение эвольвентных профилей зубьев следствию из основной теоремы зацепления.
Так как промежуток
времени t взят произвольно, то можно заключить, что в любой момент времени эвольвентные профили зубьев будут обеспечивать движение с постоянным передаточным отношением, т. е. удовлетворять следствию из основной теоремы зацепления.
Прямая n-n является линией зацепления.
Эвольвентные профили зубьев могут касаться друг друга лишь в пределах участка а0b0.
Прямая n-n является линией зацепления.
Эвольвентные профили зубьев могут касаться друг друга лишь в пределах участка а0b0.
Слайд 24Удовлетворение эвольвентных профилей зубьев следствию из основной теоремы зацепления.
Участок а0b0 называется
предельным участком линии зацепления.
Точки а0 и b0– предельными точками линии зацепления.
За пределами участка а0b0 эвольвенты пересекаются. Поэтому величины радиусов вершин зубьев ra1 и ra2 следует назначать такими, чтобы окружности вершин пересекали линию зацепления на участке а0b0.
Точки а0 и b0– предельными точками линии зацепления.
За пределами участка а0b0 эвольвенты пересекаются. Поэтому величины радиусов вершин зубьев ra1 и ra2 следует назначать такими, чтобы окружности вершин пересекали линию зацепления на участке а0b0.
Слайд 25Удовлетворение эвольвентных профилей зубьев следствию из основной теоремы зацепления.
Участок линии зацепления
а1b1, заключенный между окружностями вершин зубьев, называется активным участком линии зацепления.
Участки профилей зубьев, участвующие в зацеплении, называются активными профилями зубьев.
Участок линии осей О1О2, заключенный между окружностями вершин, называется глубиной захода hd.
Участки профилей зубьев, участвующие в зацеплении, называются активными профилями зубьев.
Участок линии осей О1О2, заключенный между окружностями вершин, называется глубиной захода hd.
Слайд 26Удовлетворение эвольвентных профилей зубьев следствию из основной теоремы зацепления.
Угол между линией
зацепления и перпендикуляром к линии осей колес называется углом зацепления αw
Соотношение между радиусом начальной и основной окружностей определяется выражением:
Соотношение между радиусом начальной и основной окружностей определяется выражением:
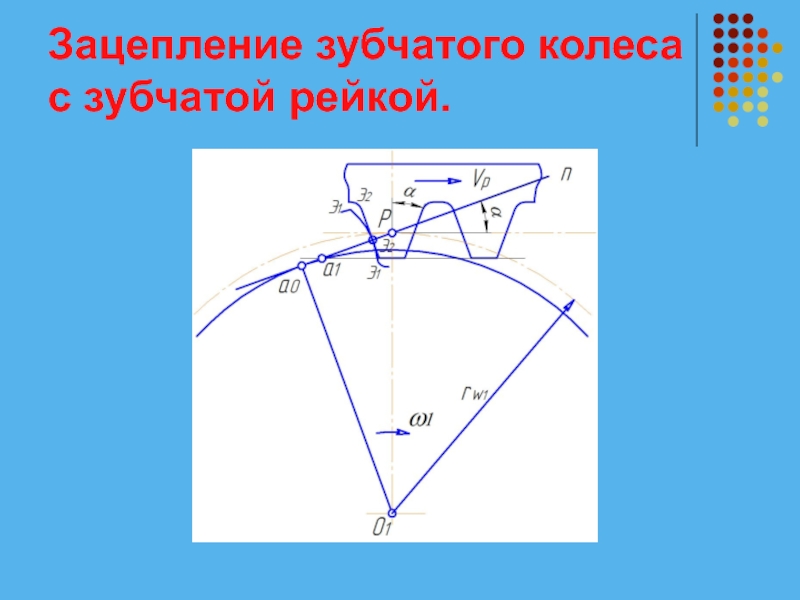
Слайд 27Зацепление зубчатого колеса с зубчатой рейкой.
Пусть радиус начальной окружности второго колеса
rw2 увеличивается и в пределе стремится к бесконечности , тогда и
Вследствие этого радиус кривизны в любой точке эвольвентного профиля зуба второго колеса и эвольвента Э2Э2 вырождается в прямую линию, перпендикулярную линии зацепления n-n.
Вследствие этого радиус кривизны в любой точке эвольвентного профиля зуба второго колеса и эвольвента Э2Э2 вырождается в прямую линию, перпендикулярную линии зацепления n-n.
Слайд 29Зацепление зубчатого колеса с зубчатой рейкой.
То есть второе зубчатое колесо превращается
в зубчатую рейку, в которой все окружности будут представлены прямыми линиями, а контур зуба получается в виде равнобедренной трапеции. Зацепление зубчатого колеса с зубчатой рейкой называется реечным зацеплением.
Линия зацепления имеет здесь только одну предельную точку а0.
Линия зацепления имеет здесь только одну предельную точку а0.
Слайд 30Зацепление зубчатого колеса с зубчатой рейкой.
В реечной передаче начальная окружность первого
колеса перекатывается без скольжения по начальной прямой рейки, при этом эвольвентный профиль зуба Э1Э1 зуба колеса огибает прямолинейный профиль Э2Э2 зуба рейки.
Реечная передача служит для преобразования вращательного движения колеса с угловой скоростью ω1 в поступательное движение рейки со скоростью vр (или наоборот).
Реечная передача служит для преобразования вращательного движения колеса с угловой скоростью ω1 в поступательное движение рейки со скоростью vр (или наоборот).