- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сильный взрыв в воздухе презентация
Содержание
- 1. Сильный взрыв в воздухе
- 2. Рассмотрим сначала, как распространяется фронт ударной волны.
- 3. Из соображений размерности получим (1) При
- 4. Мощность этого взрыва – 1 мегатонна
- 5. Граничные условия на фронте ударной волны На
- 6. Для двухатомного газа (воздух) внутренняя энергия равна
- 7. Исключая давление из системы (4), получим
- 8. Определим из (4) скорость газа сразу за
- 9. Определим также давление сразу за фронтом ударной
- 10. Автомодельные переменные Введем автомодельную переменную ,
- 11. Баланс энергии Полная энергия газа внутри ограниченной
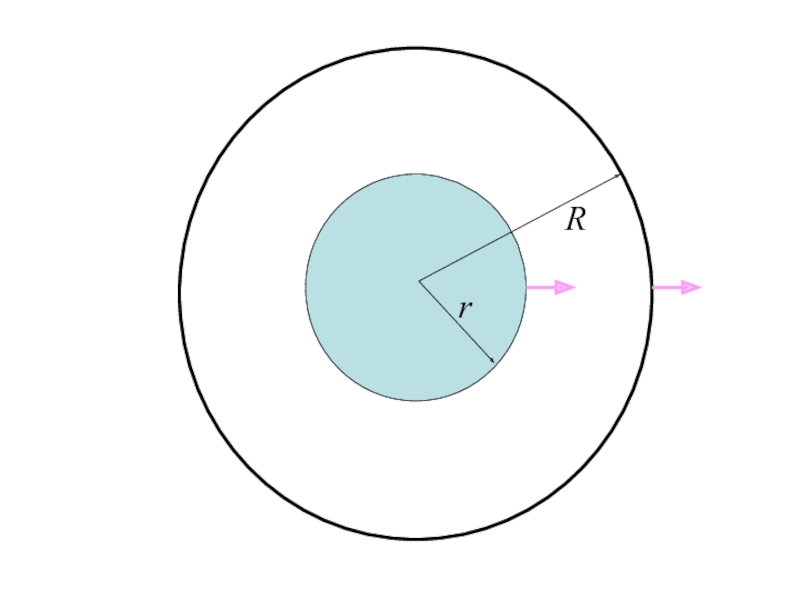
- 12. R r
- 13. За время dt через единицу сферической поверхности
- 14. С другой стороны, за это же время
- 15. Подставляя автомодельные зависимости, приведенные выше,
- 16. На малых расстояниях r
- 18. Уравнение непрерывности Обратимся теперь к уравнению непрерывности
- 19. Отсюда (константа пропорциональности выбрана так,
- 20. Видно, что ввиду очень
- 21. G(x) Зависимость плотности воздуха от расстояния до центра взрыва
- 22. Давление в области взрыва Давление воздуха выражалось
- 23. Для определения давления воспользуемся уравнением Навье-Стокса, записав
- 24. Получим обыкновенное дифференциальное уравнение первого порядка
- 25. Из этого рисунка видно, что давление
- 26. давление
- 27. Перед фронтом ударной волны давление в воздухе
- 29. Спасибо за внимание
Слайд 1Владимир Павлович Крайнов,
кафедра теоретической физики МФТИ, 10.09.2016
Лекция 2. Сильный взрыв в
Слайд 2Рассмотрим сначала, как распространяется фронт ударной волны. Радиус фронта R является
Слайд 3Из соображений размерности получим
(1)
При численном решении для воздуха коэффициент в этой
Для скорости фронта ударной волны получаем
(2)
(она, естественно, убывает со временем).
Слайд 4
Мощность этого взрыва – 1 мегатонна
тротилового эквивалента: Е = 4.18·1015
Это соответствует преобразованию в энергию
47 г урана-235 (Е = Мс2)
Слайд 5Граничные условия на фронте ударной волны
На фронте ударной волны непрерывна плотность
(3)
Слайд 6Для двухатомного газа (воздух) внутренняя энергия равна
(здесь мы воспользовались уравнением
(4)
Слайд 7Исключая давление из системы (4), получим
Исключая отношение скоростей из этой системы,
Сильная ударная волна сжимает воздух в 6 раз!
Слайд 8Определим из (4) скорость газа сразу за фронтом в лабораторной системе
(5)
Разумеется скорость частиц газа за фронтом в лабораторной системе
меньше скорости фронта: частицы газа не могут обогнать фронт.
Слайд 9Определим также давление сразу за фронтом ударной волны, исходя из системы
(5)
Далее обратимся к решению уравнений движения для внутренней области взрыва. Методика решения основана на введении автомодельной переменной, что делается в большинстве задач гидродинамики с малым числом параметров.
Слайд 10Автомодельные переменные
Введем автомодельную переменную ,
где радиус фронта ударной волны определяется
Скорость воздуха внутри области взрыва в соответствии с (2) ищем в виде , а давление -
Слайд 11Баланс энергии
Полная энергия газа внутри ограниченной ударной волной сферы постоянна. Вследствие
Радиальная скорость перемещения точек этой сферы в соответствии с (2) равна
Слайд 13За время dt через единицу сферической поверхности с этим радиусом проходит
(7)
Отметим, что здесь фигурирует скорость газа V в лабораторной системе координат. Поток энергии включает и слагаемое с давлением, соответствующее совершаемой работе, так как давление и плотность изменяются при переходе через границу сферы радиуса r, как это было ранее для фронта ударной волны (см. (3)).
Слайд 14С другой стороны, за это же время указанная поверхность расширяется на
Энергия движущегося газа, заключенная в этой области, равна
(8)
Она не содержит члена с работой, в отличие от (7). Приравнивая (7) и (8) друг другу, находим уравнение баланса энергии:
Слайд 15
Подставляя автомодельные зависимости, приведенные выше, перепишем это уравнение в виде
Отсюда находим
(9)
Слайд 16На малых расстояниях r
Из (9) тогда следует, что
Для скорости газа получим
(10)
Слайд 17 Если
то согласно
Видно, что расхождение между этой скоростью газа и скоростью газа в окрестности точки взрыва
невелико. Это оправдывает сделанное выше приближение для скорости газа.
Слайд 18Уравнение непрерывности
Обратимся теперь к уравнению непрерывности (в сферической системе координат)
Подставляя выражение
перепишем это уравнение в виде
Слайд 19Отсюда
(константа пропорциональности выбрана так, чтобы плотность газа на внутренней поверхности
Слайд 20
Видно, что ввиду очень резкой зависимости от расстояния r практически внутри
Слайд 22Давление в области взрыва
Давление воздуха выражалось через безразмерную автомодельную переменную соотношением
На
Слайд 23Для определения давления воспользуемся уравнением Навье-Стокса, записав его в сферической системе
(11)
Подставляем в это уравнение величины, выраженные через автомодельную переменную :
Тогда все слагаемые в (11) содержат r/t2
Слайд 24Получим обыкновенное дифференциальное уравнение первого порядка
Его решение при условии
Отношение давления внутри области взрыва к давлению на фронте ударной волны равно
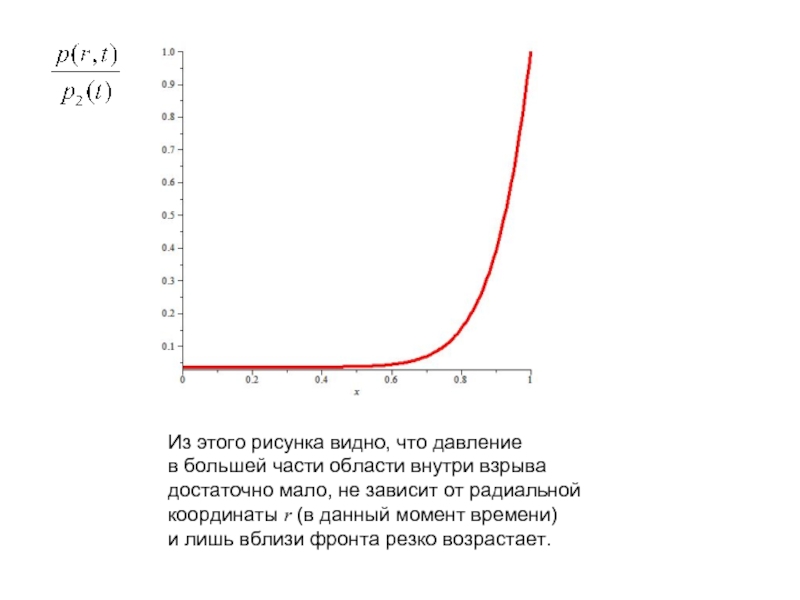
Слайд 25Из этого рисунка видно, что давление
в большей части области внутри
достаточно мало, не зависит от радиальной
координаты r (в данный момент времени)
и лишь вблизи фронта резко возрастает.
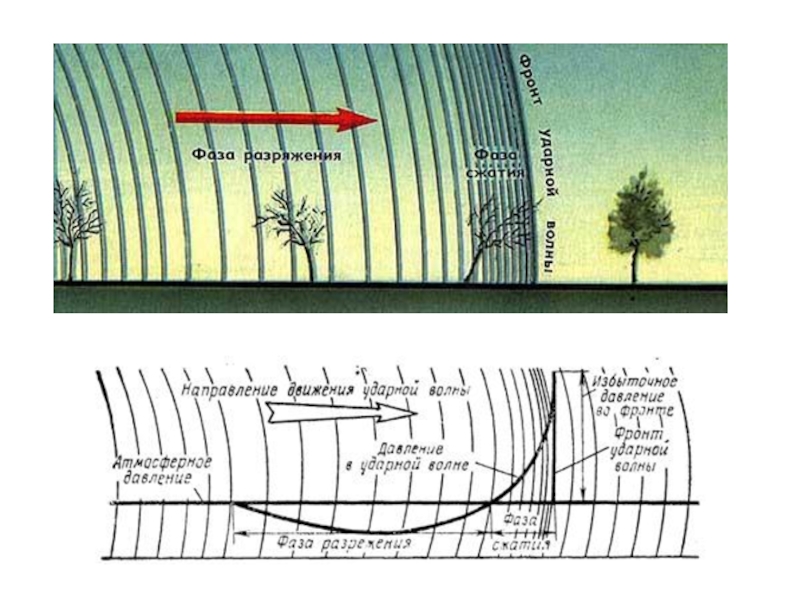
Слайд 27Перед фронтом ударной волны давление в воздухе равно атмосферному давлению. С
Фаза разрежения внутри области взрыва