- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сила давления жидкости на плоские и криволинейные стенки презентация
Содержание
- 1. Сила давления жидкости на плоские и криволинейные стенки
- 2. 1. Сила давления жидкости на плоскую стенку
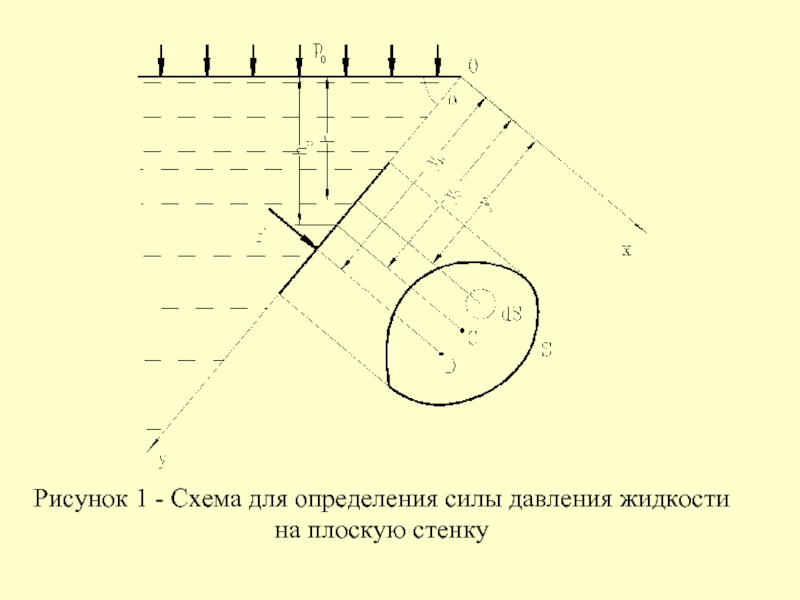
- 3. Рисунок 1 - Схема для определения силы давления жидкости на плоскую стенку
- 4. Давление в каждой точке стенки направлено по
- 5. Для получения полной силы давления F проинтегрируем
- 6. Таким образом, полная сила давления жидкости на
- 7. Найдем точку приложения силы давления на плоскую
- 8. Выразим координату точки приложения силы yD и
- 9. 2. Сила давления жидкости на криволинейные стенки
- 10. Рисунок 2 - Схема для определения силы
- 11. На рисунке показана реакция стенки на жидкость,
- 12. По вычисленным составляющим Fz и Fx найдем
Слайд 2 1. Сила давления жидкости на плоскую стенку
Найдем силу давления жидкости
Сила характеризуется тремя параметрами:
– направлением:
– величиной;
– точкой приложения.
Слайд 4 Давление в каждой точке стенки направлено по нормали к ней, следовательно,
Ось 0x направим по линии пересечения стенки со свободной поверхностью жидкости, а ось 0y – перпендикулярно к этой линии в плоскости стенки.
Вычислим элементарную силу давления, приложенную к бесконечно малой площадке dS:
где p0 – давление на свободную поверхность;
h – глубина расположения площадки dS.
Слайд 5 Для получения полной силы давления F проинтегрируем полученное выражение по всей
Полученный интеграл представляет собой статический момент площади S относительно оси 0x и равен произведению этой площади на координату ее центра масс (точка С), то есть
Следовательно,
где hC, pC – глубина расположения центра масс площадки и давление в этой точке.
Слайд 6 Таким образом, полная сила давления жидкости на плоскую стенку равна произведению
При давлении на свободную поверхность, отличном от нормального (атмосферного), сила давления на поверхность стенки определяется по выражению
где рман. и рвак. – манометрическое и вакуумметрическое давление
Слайд 7 Найдем точку приложения силы давления на плоскую стенку.
Сила F0 будет
Слайд 8 Выразим координату точки приложения силы yD и подставим значения сил Fж
где – момент инерции площади S относительно оси 0x.
Учитывая, что
где Jx0 – момент инерции площади S относительно горизонтальной оси, лежащей в плоскости стенки и проходящей через ее центр масс.
Отсюда, точка приложения силы Fж имеет координату
ИЛИ
Слайд 9 2. Сила давления жидкости на криволинейные стенки
Если поверхность имеет произвольную форму,
– жидкость расположена сверху;
– жидкость расположена снизу.
Слайд 10Рисунок 2 - Схема для определения силы давления жидкости на криволинейную
y
x
z
Слайд 11 На рисунке показана реакция стенки на жидкость, которая, как известно, равна
Fz = ρgVт.д., где Vт.д. – объем тела давления;
Объем тела давления – это объем жидкости, ограниченный рассматриваемой стенкой и вертикальной проекцией, проведенной через контур рассматриваемой стенки.
Условие равновесия в горизонтальном направлении:
Fx = ρ g hC Szy.
где Szy – площадь проекции стенки на вертикальную плоскость zOy
Слайд 12 По вычисленным составляющим Fz и Fx найдем величину силы давления жидкости
Угол наклона силы давления к горизонтальной плоскости