- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Реологические свойства биологических объектов. Гемодинамика презентация
Содержание
- 1. Реологические свойства биологических объектов. Гемодинамика
- 3. Биореология. Вязкость. Биореология – наука о деформациях
- 5. Физический смысл вязкости Физический смысл вязкости находят
- 8. Ньютоновские и неньютоновские жидкости Ньютоновскими называют жидкости,
- 11. Методы измерения вязкости крови Совокупность методов измерения
- 12. Метод Стокса Вискозиметр Гесса Ротационный метод вискозиметрии
- 17. Уравнение неразрывности Условие неразрывности струи: при стационарном
- 24. Гемодинамика – раздел биомеханики, который изучает законы
- 25. Основные положения гемодинамики Основной причиной движения крови
- 27. Работа и мощность сердца Работа, совершаемая сердцем,
- 29. Ударным объемом Vуд называют объем крови, который
- 30. Измерение артериального давления Одним из основных гемодинамических
- 31. Среднее артериальное давление
- 33. Клинический метод измерения АД Клинический метод измерения
- 36. Физическая функция каждого элемента сердечно-сосудистой системы
- 37. Сердечно-сосудистая система замкнута, поэтому для обеспечения течения
- 38. Крупные сосуды являются согласующим элементом между сердцем
- 39. Механические характеристики сосудов Прохождение крови по сосудам
- 40. Закон Гука Упругие деформации в теле подчиняются закону
- 45. Уравнение Лапласа Т= (Рвн - Рнар )∙r/h
- 46. Пульсовая волна Пульсовой волной называют волну повышенного
- 49. Задача 1. Скорость пульсовой волны в артериях
- 50. Решение. v= √E⋅h/(2ρ∙r). Следовательно: E⋅h=2ρ∙r∙v2, откуда:
- 51. Задача 2. 2. Как изменится
- 52. 3.Скорость потока крови в капиллярах равна примерно
- 53. 4. Найти скорость верхнего слоя жидкости, вязкость
- 54. Решение. Решение Согласно
- 55. СПАСИБО ЗА ВНИМАНИЕ!
Слайд 1Лекция 4. Реологические свойства биологических объектов. Гемодинамика
Биологические жидкости и их характеристики
Уравнение
Ньютоновские и неньютоновские жидкости
Вязкость крови и методы ее измерения
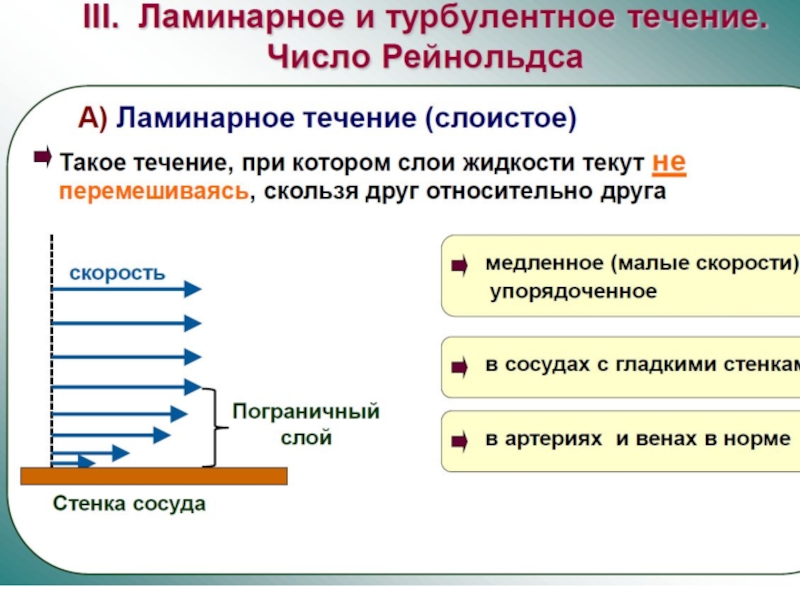
Характер течения жидкости. Число Рейнольдса
Объемная скорость течения.Уравнение Пуазейля. Гидравлическое сопротивление сосудов
Слайд 3Биореология. Вязкость.
Биореология – наука о деформациях и текучести жидких сред организма.
При
Слайд 5Физический смысл вязкости
Физический смысл вязкости находят из уравнения Ньютона.
Вязкостью называют силу,
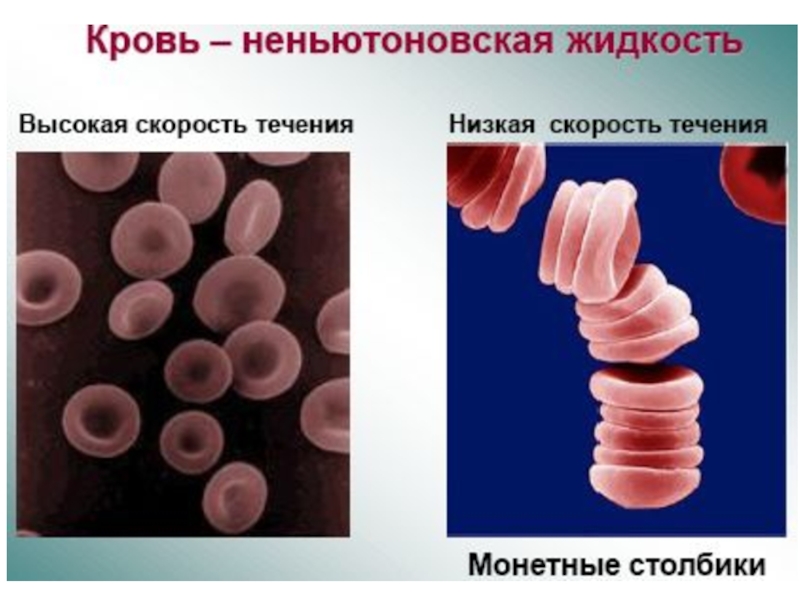
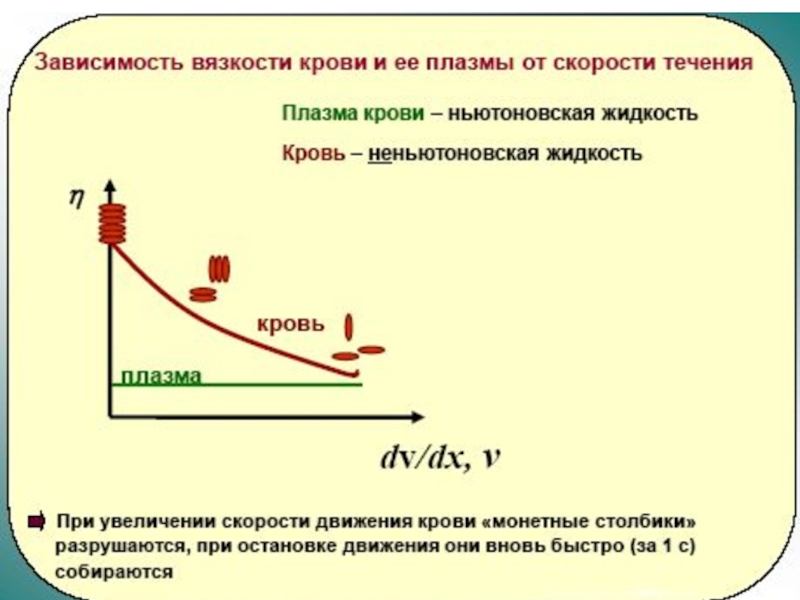
Слайд 8Ньютоновские и неньютоновские жидкости
Ньютоновскими называют жидкости, коэффициент вязкости которых зависит только
Неньютоновскими называют жидкости, коэффициент вязкости которых зависит не только от природы вещества и температуры, но также и от условий течения жидкости, в частности от градиента скорости.
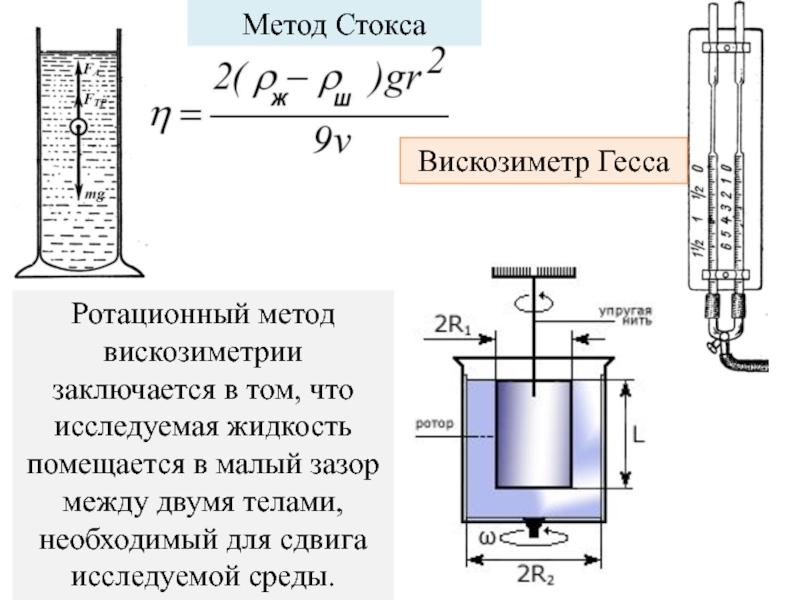
Слайд 11Методы измерения вязкости крови
Совокупность методов измерения вязкости жидкости называется вискозиметрией. Прибор
Слайд 12Метод Стокса
Вискозиметр Гесса
Ротационный метод вискозиметрии заключается в том, что исследуемая жидкость
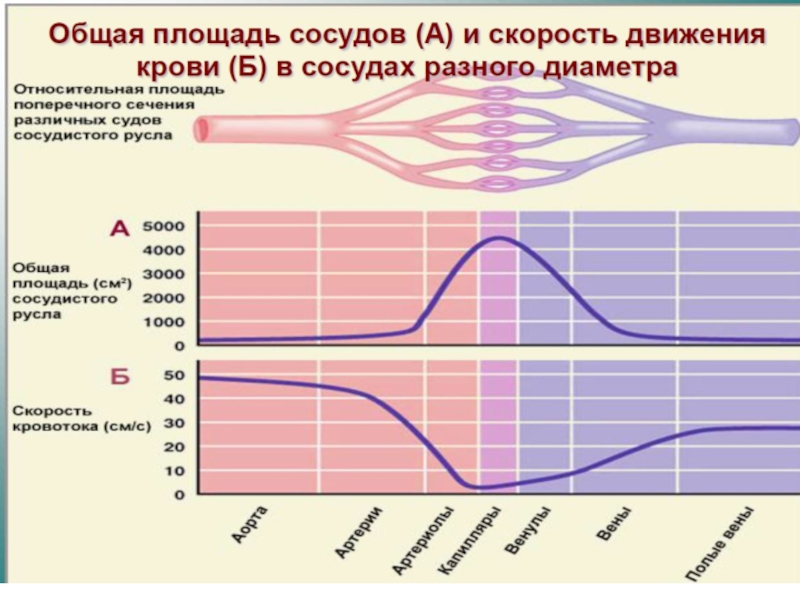
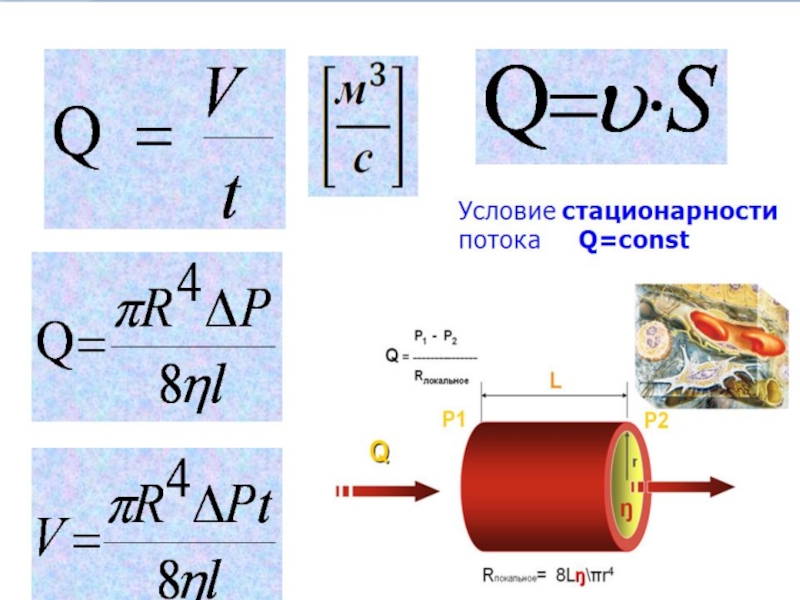
Слайд 17Уравнение неразрывности
Условие неразрывности струи: при стационарном течении несжимаемой жидкости через любые
Q1=Q2=Q3=(Sn⋅ vn)=…=const
v2=(S1⋅ v1)/S2 =(r1/r2 )2∙v1=(d1/d2 )2∙v1
Слайд 24Гемодинамика – раздел биомеханики, который изучает законы движения крови по сосудам.
Основной
Разность давлений обеспечивает такой важный гемодинамический параметр как объемная скорость кровотока.
Слайд 25Основные положения гемодинамики
Основной причиной движения крови по сосудам является разность давлений
Слайд 27Работа и мощность сердца
Работа, совершаемая сердцем, затрачивается на преодоление сил давления
Слайд 29Ударным объемом Vуд называют объем крови, который выталкивается из левого желудочка
Среднее давление в норме 13⋅103 Па, средняя скорость движения крови в аорте составляет 0,5 м/с. При ЧСС= 60 уд/мин за одно сокращение сердце выполняет работу в 1 Дж, а мощность сердца равна 3,3 Вт
Работа и мощность сердца
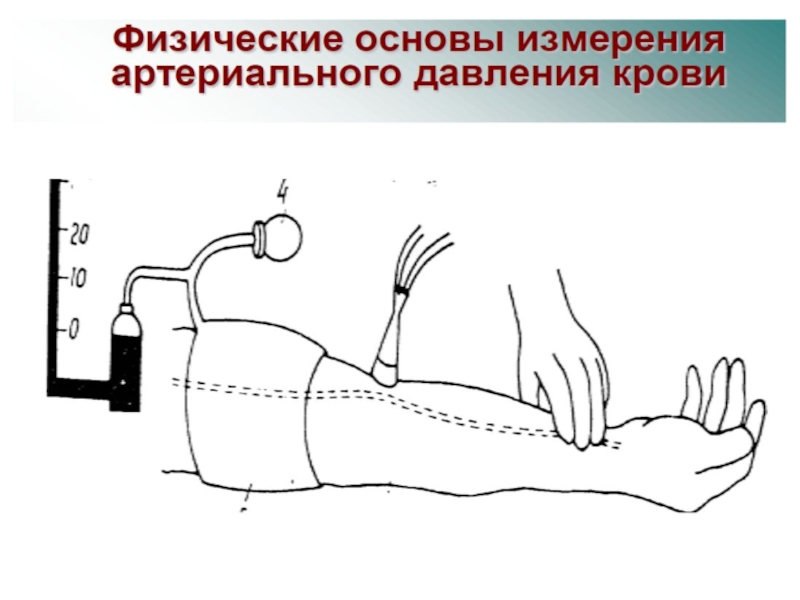
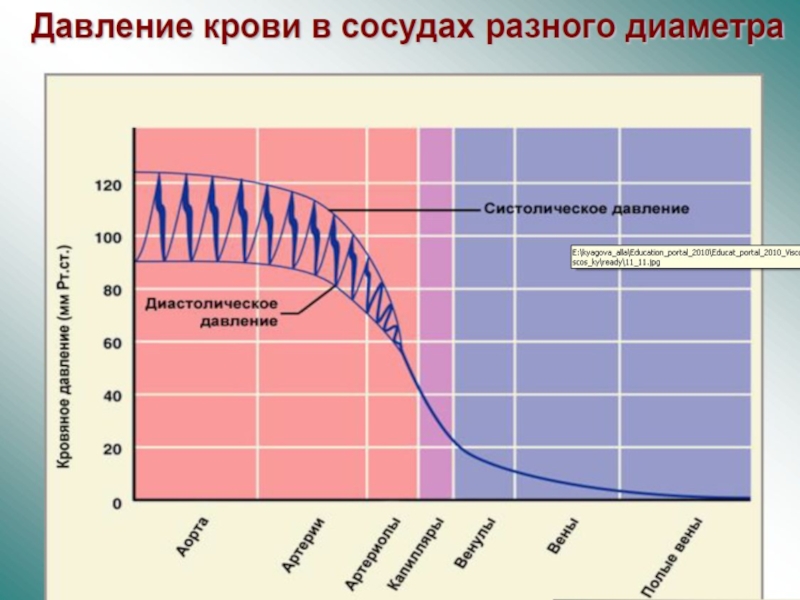
Слайд 30Измерение артериального давления
Одним из основных гемодинамических показателей является артериальное давление.
Давление -
Максимальное Рс и минимальное Рд давление находят при помощи метода Короткова или осцилляторным методом. Среднее давление крови находят по формуле:
Слайд 33Клинический метод измерения АД
Клинический метод измерения АД основан на регистрации систолического
Слайд 36Физическая функция каждого элемента сердечно-сосудистой системы
Основная функция сердечно-сосудистой системы -
Слайд 37Сердечно-сосудистая система замкнута, поэтому для обеспечения течения крови в ней должен
Слайд 38Крупные сосуды являются согласующим элементом между сердцем и мелкими сосудами. При
Слайд 39Механические характеристики сосудов
Прохождение крови по сосудам вызывает их деформацию ─ изменение размеров или
.Упругая деформация ─ деформация, которая исчезает после снятия внешней нагрузки (т.е. тело полностью восстанавливает форму и размеры).
Пластическая деформация ─ деформация, которая не исчезает после снятия внешней нагрузки (т.е. тело не восстанавливает форму и размеры).
Слайд 40Закон Гука
Упругие деформации в теле подчиняются закону Гука (закону упругих деформаций): механическое напряжение (σ
σ = ε⋅E;
где: ε =Δl/l0= (l - l0)/l0 – относительная деформация; E – модуль упругости (модуль Юнга)
Слайд 45Уравнение Лапласа
Т= (Рвн - Рнар )∙r/h
Где Т- тонус сосуда;
Рвн -
Рнар - наружное давление;
r – радиус сосуда;
h – толщина стенки сосуда
Слайд 46Пульсовая волна
Пульсовой волной называют волну повышенного давления, вызванную выбросом крови из
Слайд 49Задача 1.
Скорость пульсовой волны в артериях составляет 10 м/с. Чему равен
Слайд 50Решение.
v= √E⋅h/(2ρ∙r). Следовательно:
E⋅h=2ρ∙r∙v2, откуда:
E =(2ρ∙r∙v2)/h
Проверка размерности:
[Па] =[кг∙м∙м2/ м4∙с2] = [Па]
Ответ: E =( 2∙1,05·103∙8∙102 =1,68∙106 Па
Слайд 51Задача 2.
2. Как изменится скорость распространения пульсовой волны в сосуде при
Решение
Слайд 523.Скорость потока крови в капиллярах равна примерно v1 = 30 мм/мин,
Решение
Согласно уравнению неразрывности:
S2/S1 =v1/v2=(45/0,05)=900
Слайд 534. Найти скорость верхнего слоя жидкости,
вязкость которой составляет 1 мПа⋅с, если
при
действует силой 20мН на 200м2 дна русла.
Решение.
Согласно уравнению Ньютона:
F=(η⋅S⋅vв)/h.
vв = (F ⋅ h)/(η⋅S)=(20⋅10-3 ⋅5)/(200⋅10-3)=
=0,5(м/с). Ответ: vв = 0,5(м/с).
Слайд 54
Решение.
Решение
Согласно формуле для числа Рейнольдса: Re=(ρ⋅v⋅d)/η; откуда: d=(Re⋅η)/(ρ⋅v)
m=(ρ⋅V)=(ρ⋅v⋅π⋅d2⋅t)/4; т.о.: ρ⋅v=4m/(π⋅d2⋅t), тогда:
d= 4m/(Re⋅η⋅π⋅t)=(4⋅0,36)/(2⋅103⋅4⋅10-3⋅3,14⋅2)
≈0,029(м). Ответ: d≈0,029(м)
5.Какой диаметр аорты, если при прохождении через нее крови массой 0,36 кг за 2 с течение сохранялось ламинарным? Вязкость крови 4 мПас, а критическое число Рейнольдса 2000.









































![Решение. v= √E⋅h/(2ρ∙r). Следовательно:E⋅h=2ρ∙r∙v2, откуда:E =(2ρ∙r∙v2)/hПроверка размерности:[Па] =[кг∙м∙м2/ м4∙с2] = [Па] Ответ: E =( 2∙1,05·103∙8∙102](/img/tmb/3/266871/caa4f10dc146f96abe41ce9bc0cc208a-800x.jpg)










