- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Рекуррентные оптимальные алгоритмы фильтрации случайных процессов. Фильтр Калмана-Бьюси презентация
Содержание
- 1. Рекуррентные оптимальные алгоритмы фильтрации случайных процессов. Фильтр Калмана-Бьюси
- 2. На предыдущих лекциях мы обсудили вопросы дискретной фильтрации случайных последовательностей .
- 3. Содержание Случайные процессы и методы их описания.
- 4. Случайные процессы и методы их описания
- 8. Спектральная плотность, соответствующая этой функции, имеет вид
Слайд 1Санкт-Петербург, 2016
Неделя 10
Рекуррентные оптимальные алгоритмы фильтрации случайных процессов. Фильтр Калмана-Бьюси
Методы обработки
Автор: д.т.н., профессор Степанов Олег Андреевич
Слайд 2На предыдущих лекциях мы обсудили вопросы дискретной фильтрации случайных последовательностей
.
Слайд 3Содержание
Случайные процессы и методы их описания.
Понятие формирующего фильтра и его свойства.
Постановка
Связь непрерывных и дискретных алгоритмов фильтрации.
Слайд 5
Случайным процессом x(t) в скалярном случае называется такая функция времени
Корреляционная функция случайного процесса
. (1)
Стационарным процессом в широком смысле называется такой процесс, у которого математическое ожидание от времени не зависит, а корреляционная функция зависит от разности аргументов
; . (2)
Случайные процессы и методы их описания
Определение случайного процесса
Слайд 6
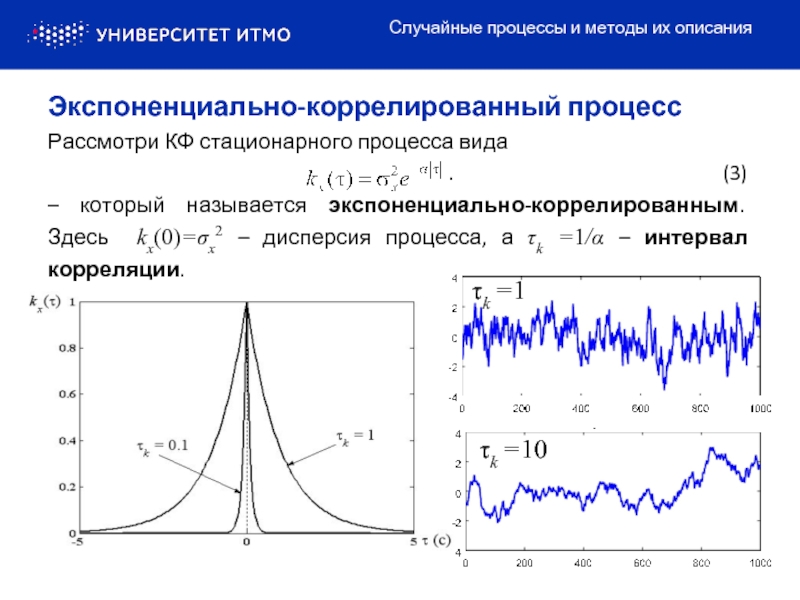
Рассмотри КФ стационарного процесса вида
. (3)
– который
τk =1
τk =10
Экспоненциально-коррелированный процесс
Случайные процессы и методы их описания
Слайд 7
Спектральная плотность также используется для описания стационарных процессов и представляет
. (4)
Справедливо и обратное представление
. (5)
В силу четного характера функций Sx (ω) и kx(τ), приведенные соотношения можно записать:
(6)
(7)
Спектральная плотность случайного процесса
Случайные процессы и методы их описания
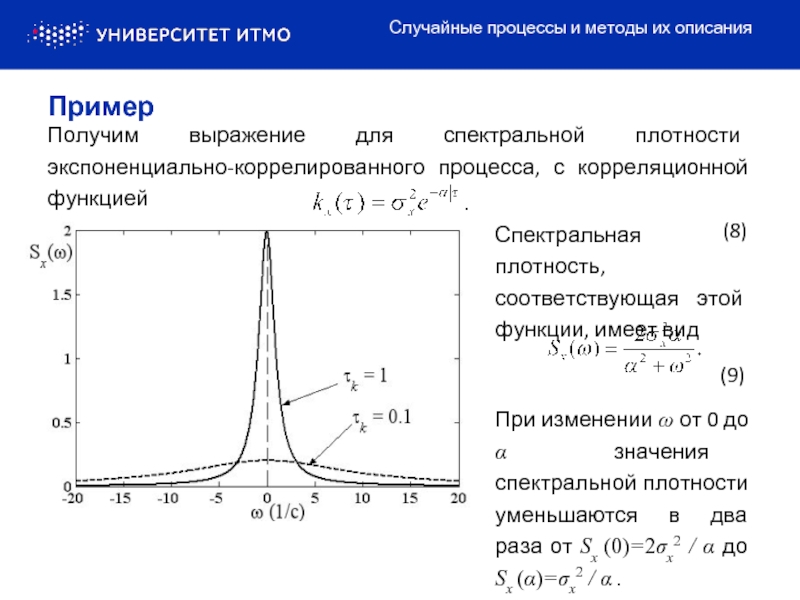
Слайд 8Спектральная плотность, соответствующая этой функции, имеет вид
(9)
При изменении
Получим выражение для спектральной плотности экспоненциально-коррелированного процесса, с корреляционной функцией
(8)
Пример
Случайные процессы и методы их описания
Слайд 9
ω
Sx (ω)
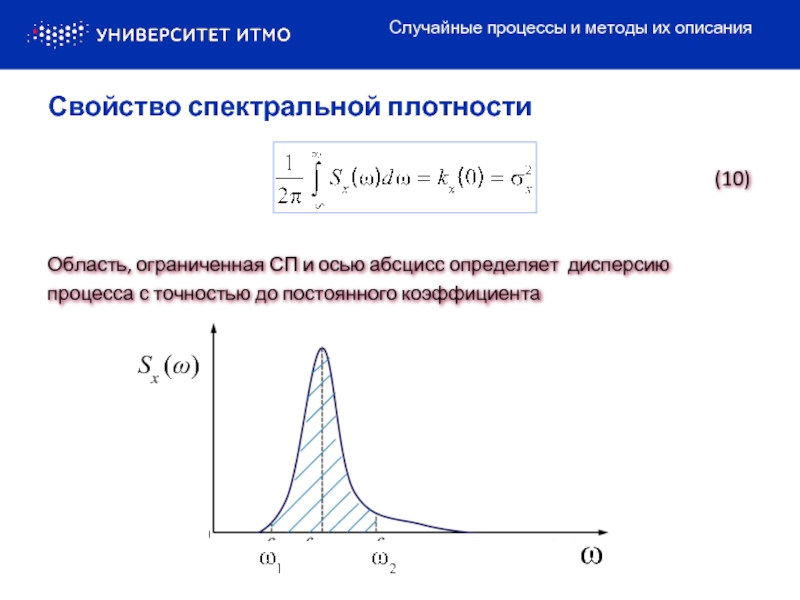
Область, ограниченная СП и осью абсцисс определяет дисперсию процесса
(10)
Случайные процессы и методы их описания
Свойство спектральной плотности
Слайд 10
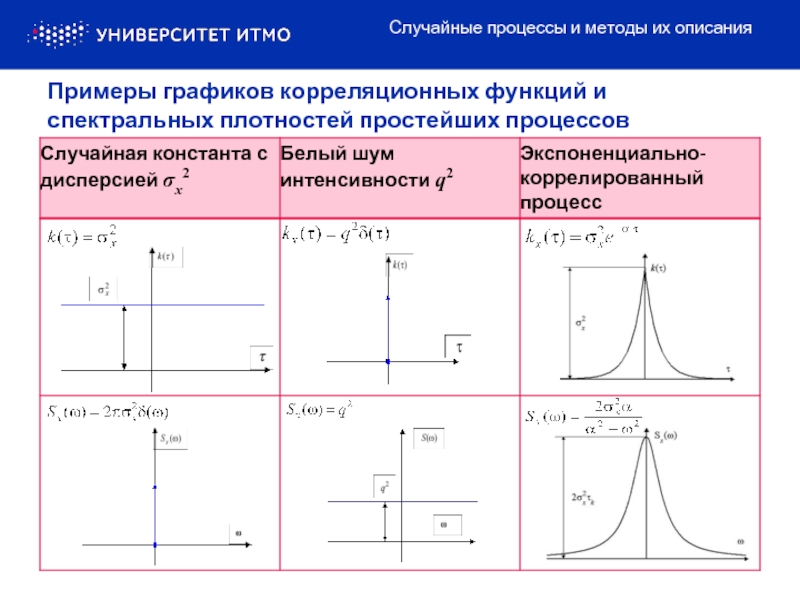
Процесс с постоянной спектральной плотностью во всем диапазоне частот,
Корреляционная функция БШ имеет вид
(11)
вид который вытекает из следующего представления о дельта-функции
(12)
Особенности БШ:
дисперсия БШ бесконечна;
значения процесса в разные моменты времени не коррелированны.
Случайные процессы и методы их описания
Белый шум