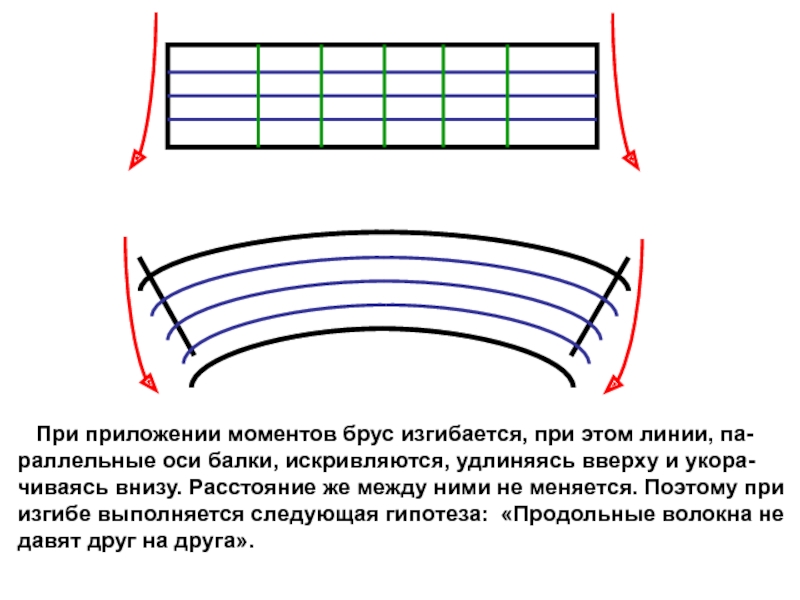
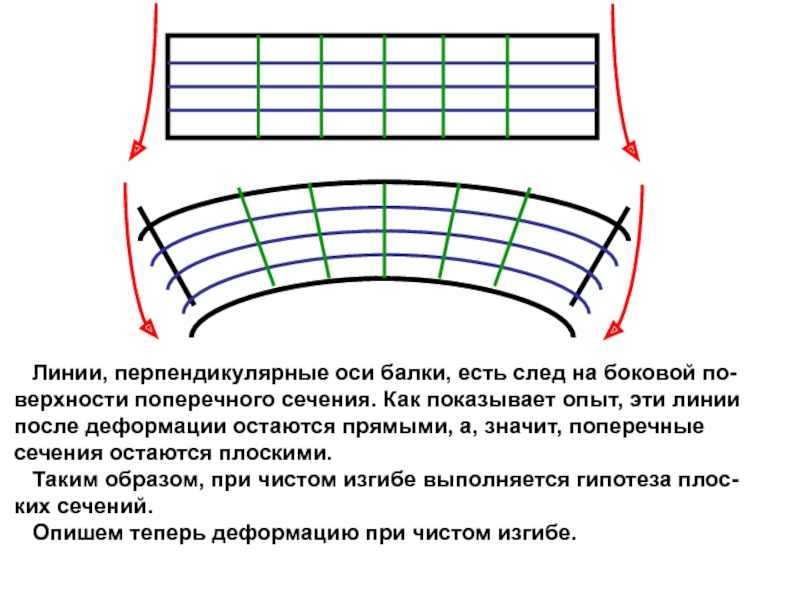
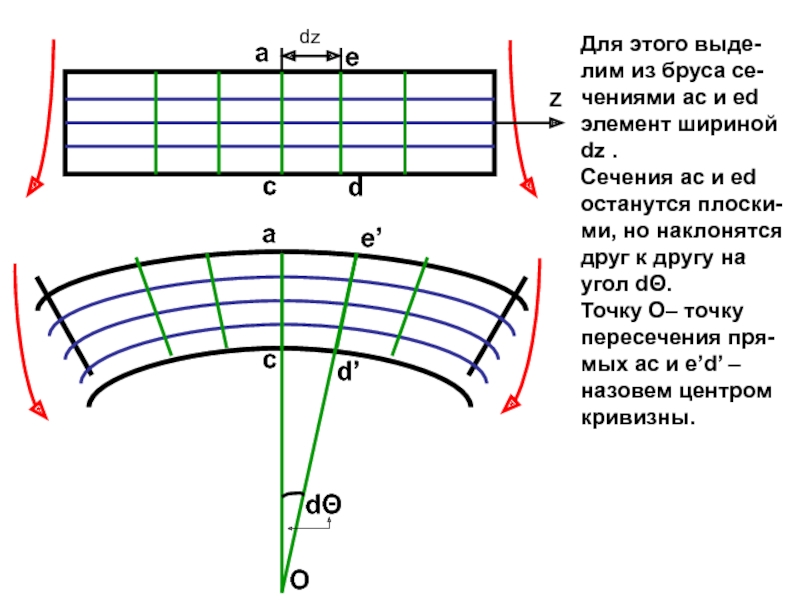
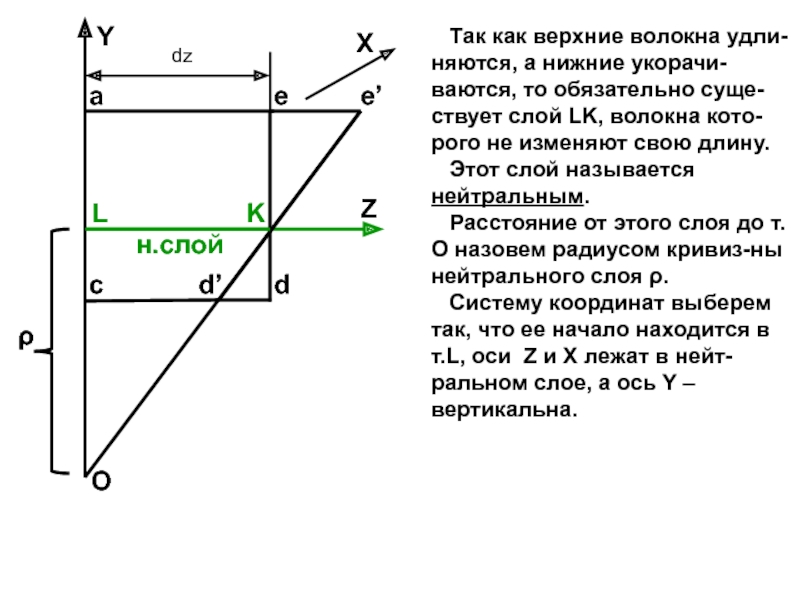
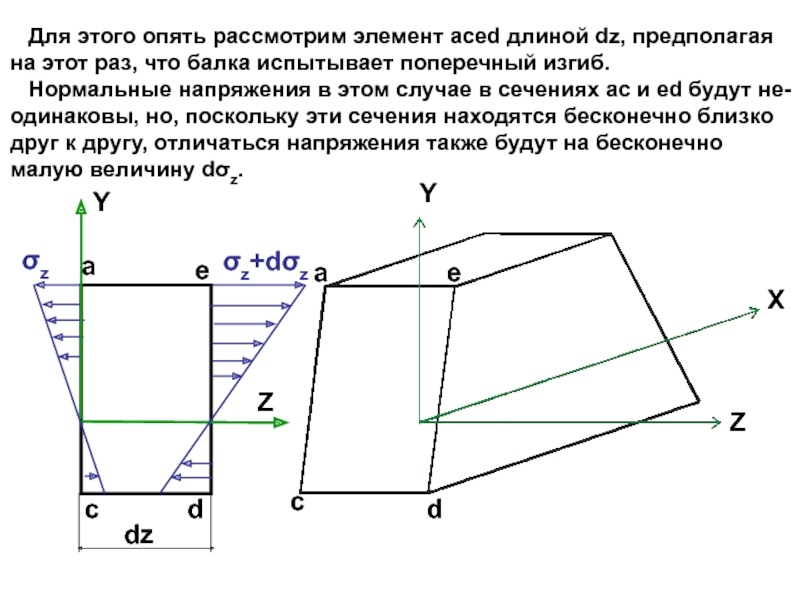
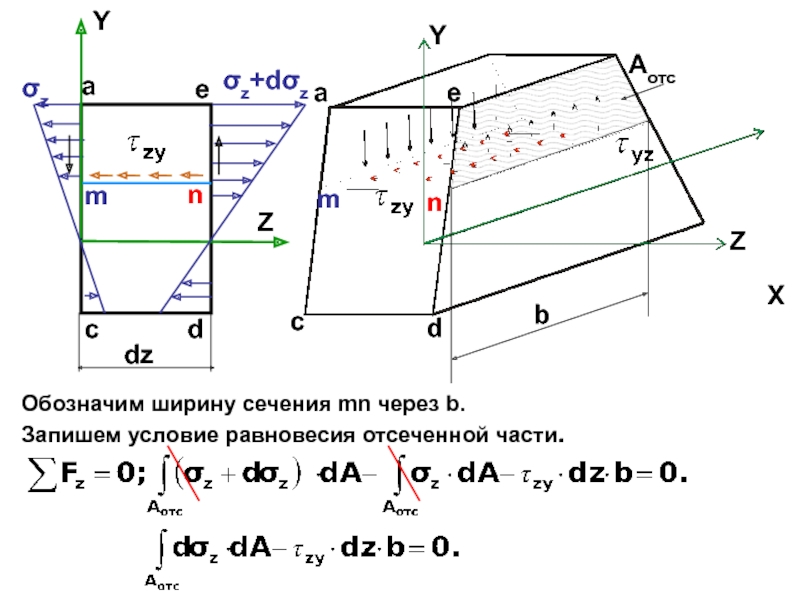
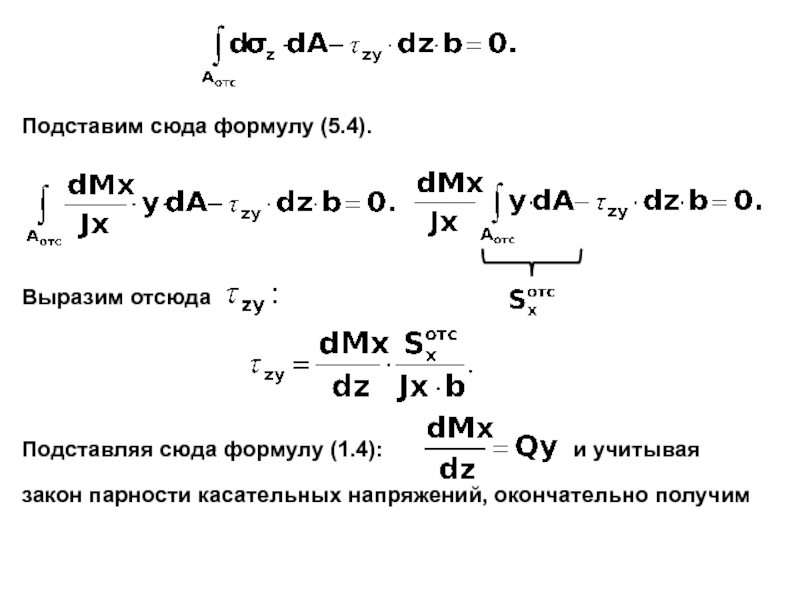
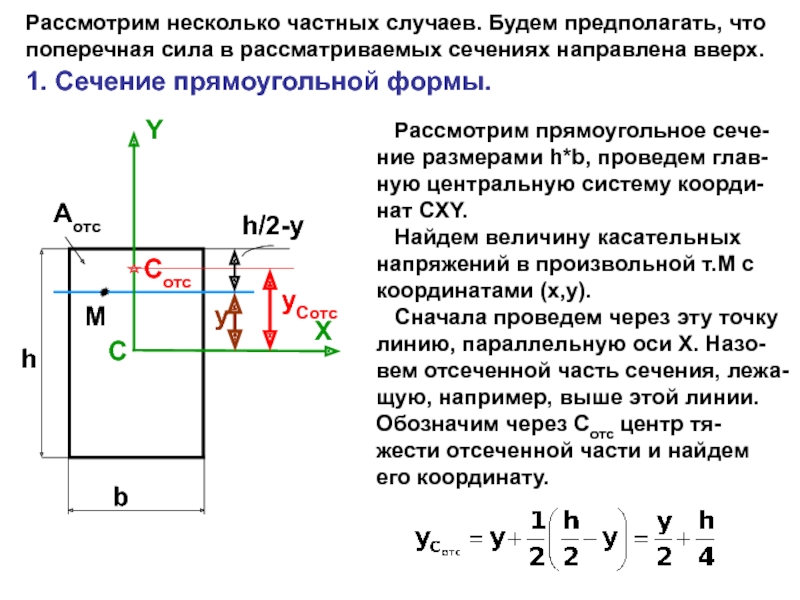
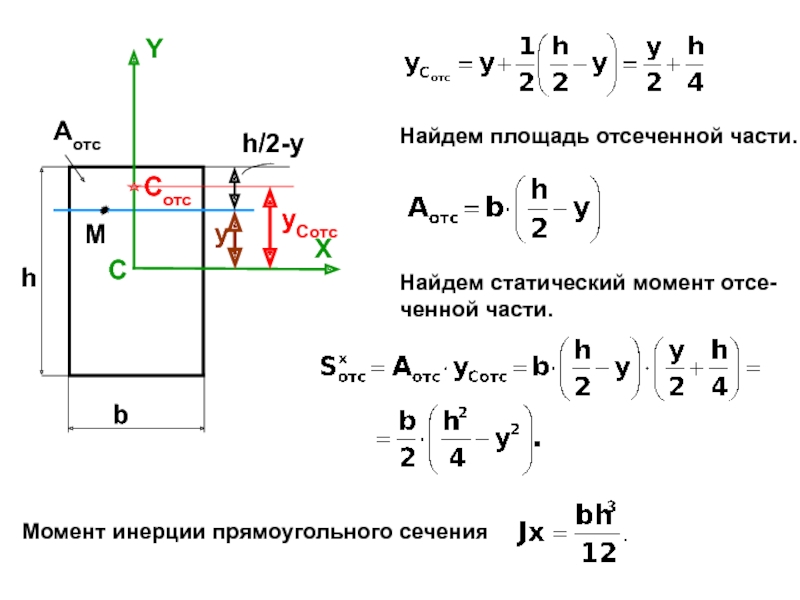
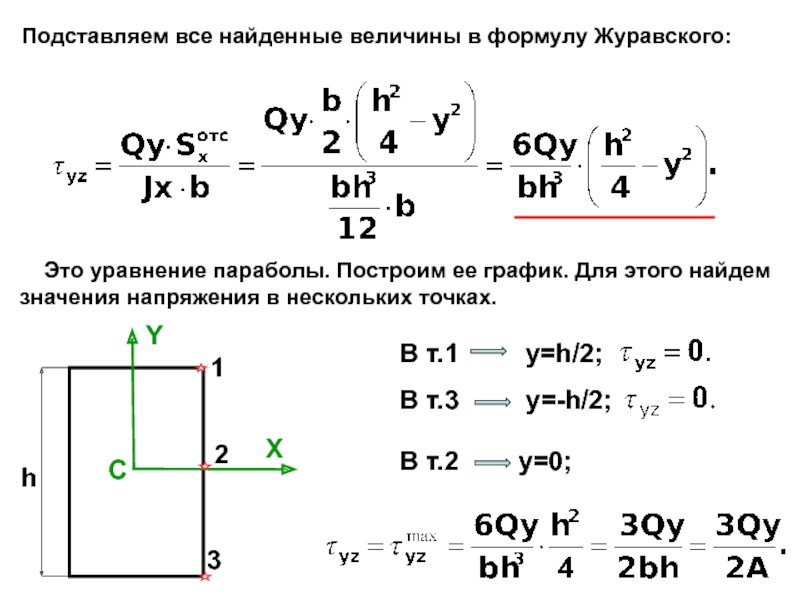
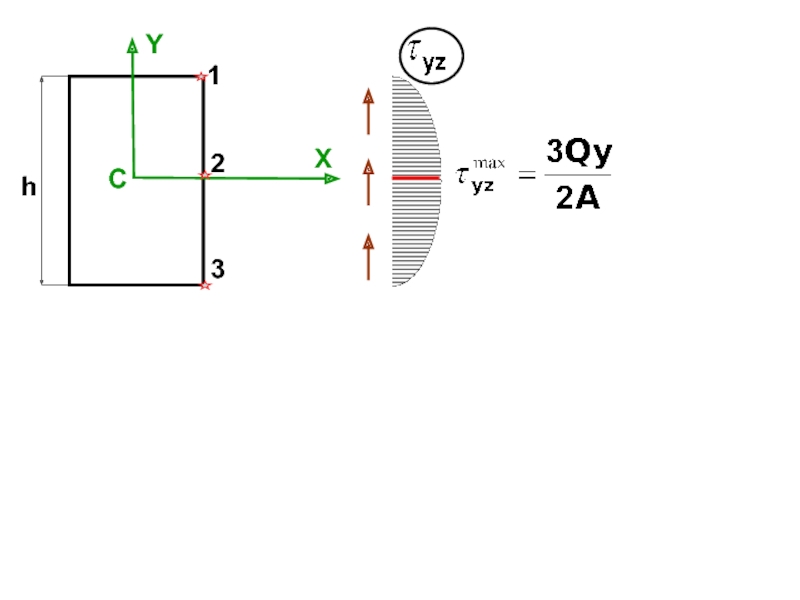
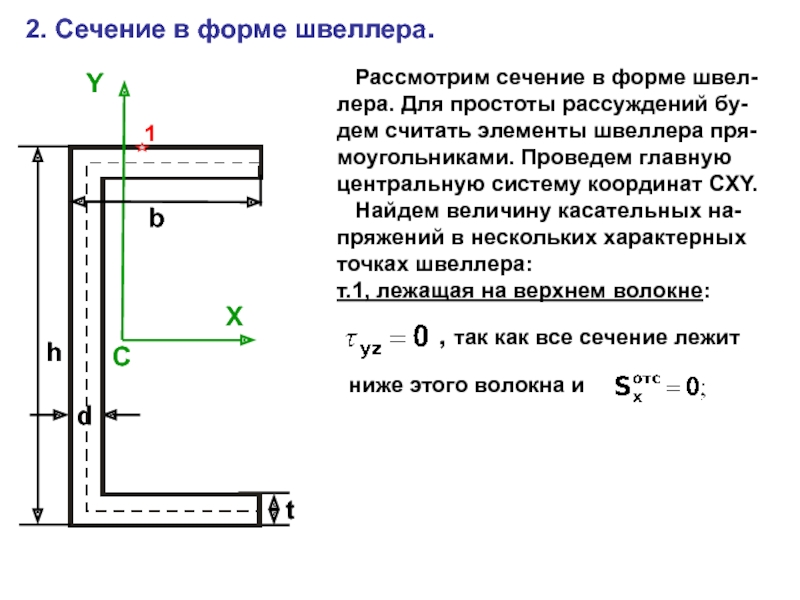
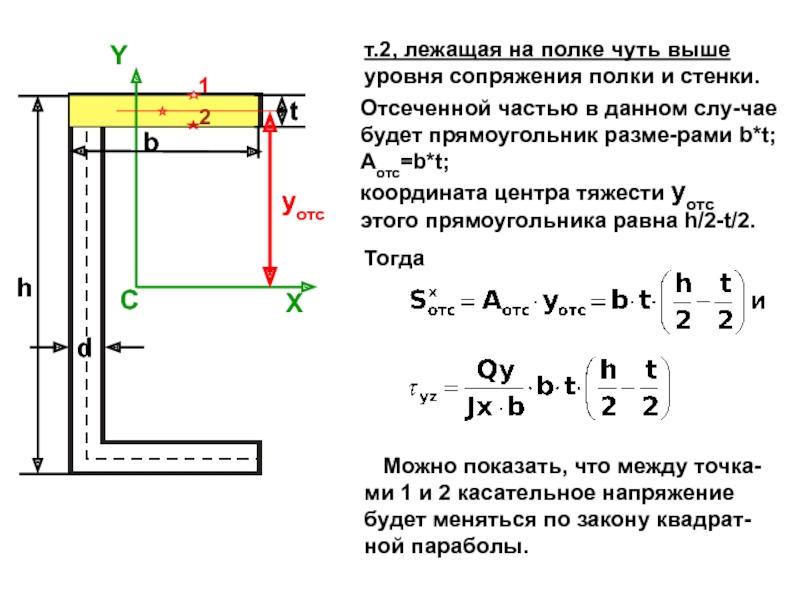
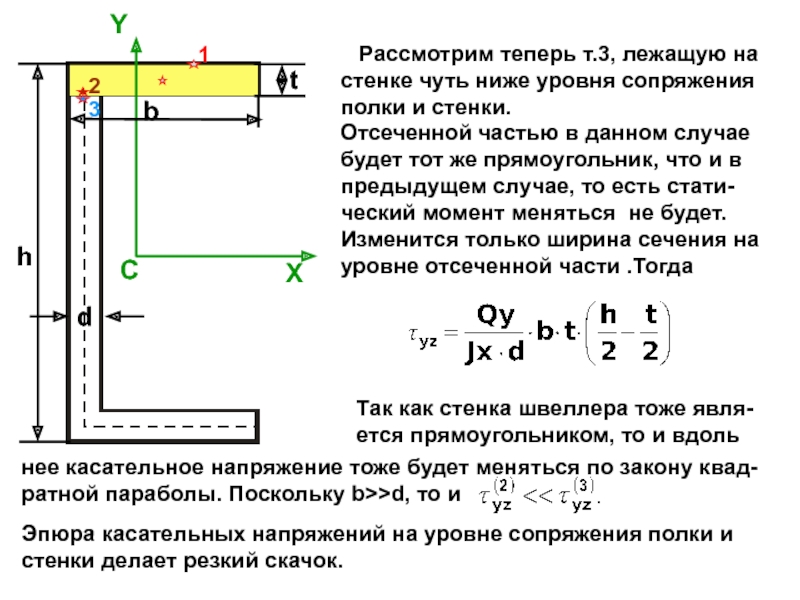
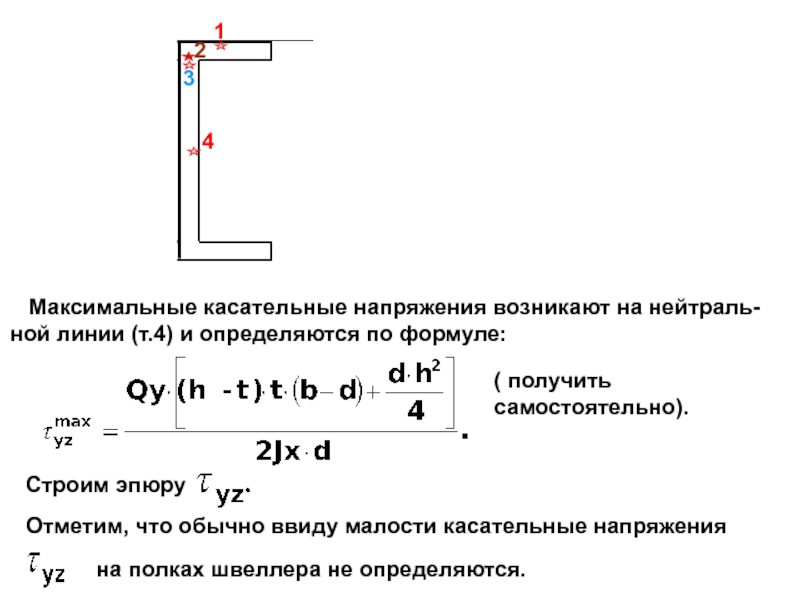
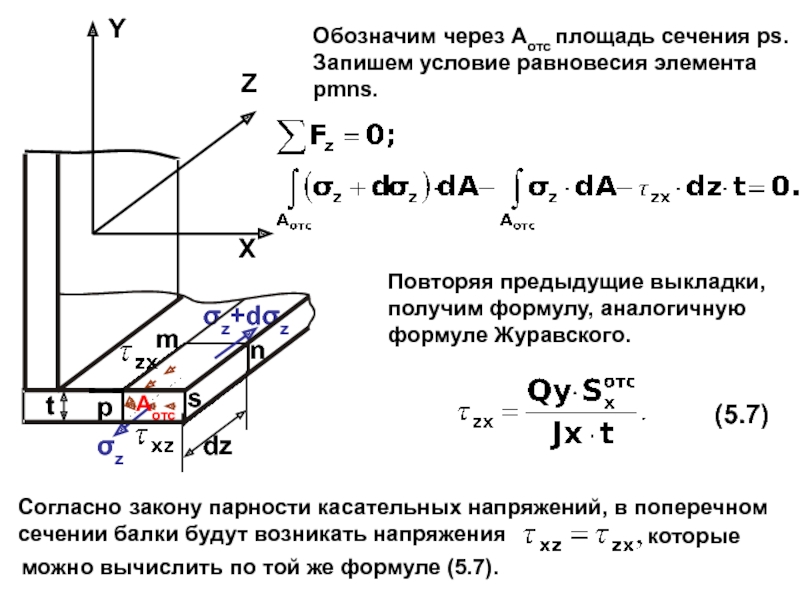
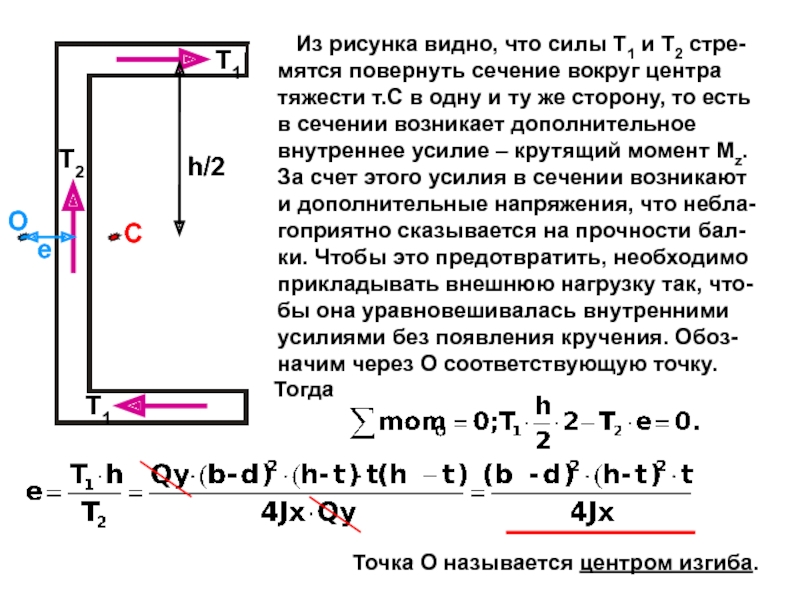
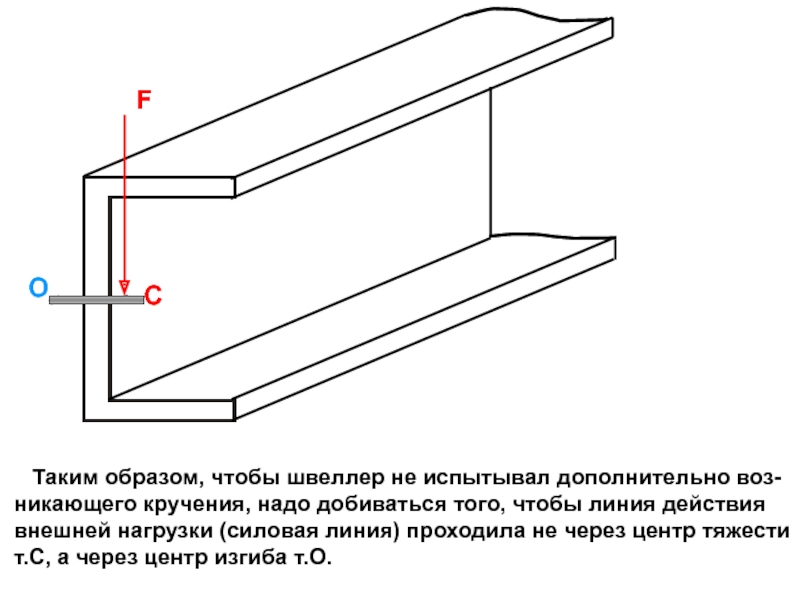
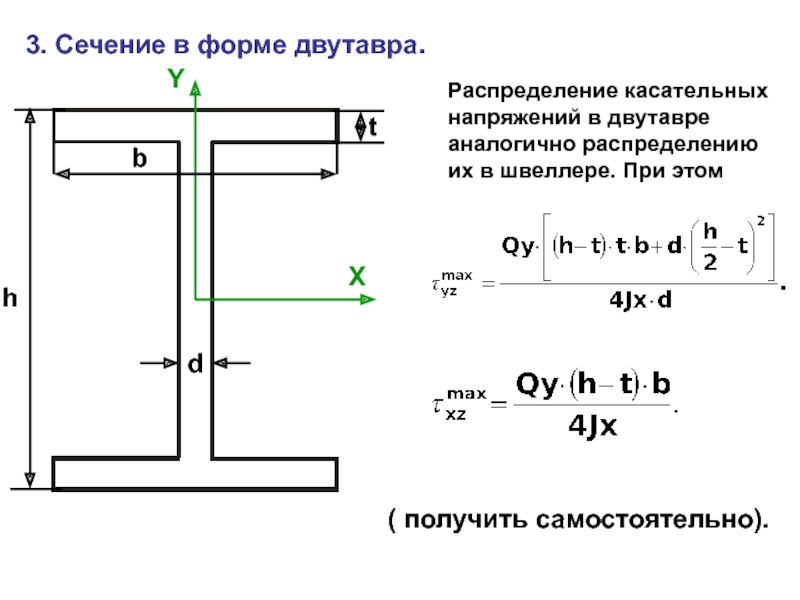
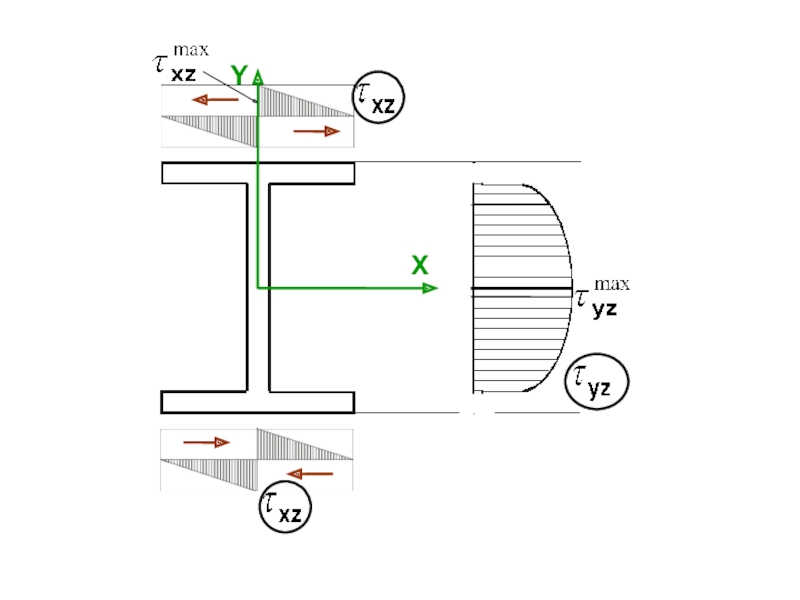
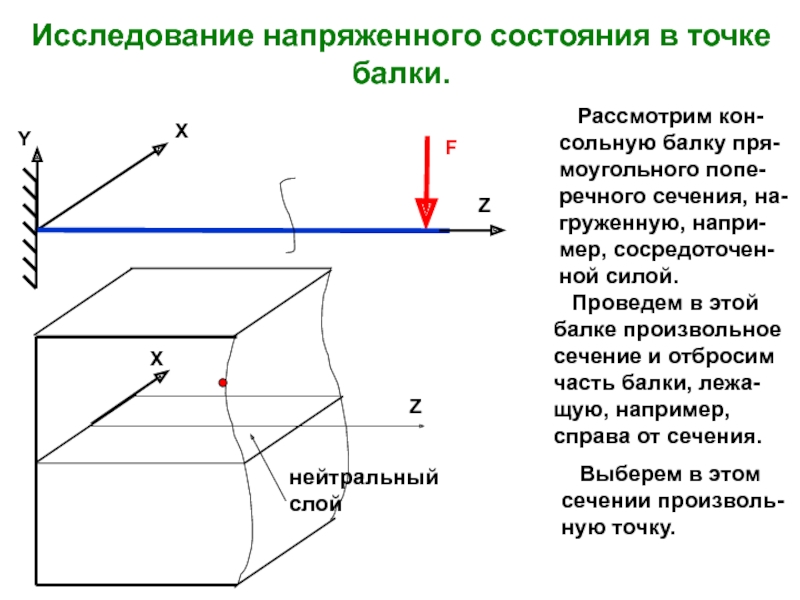
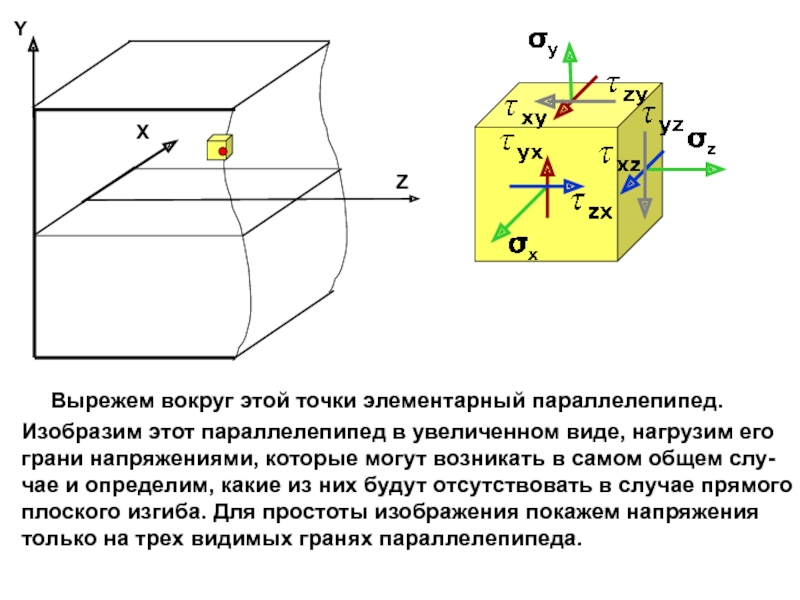
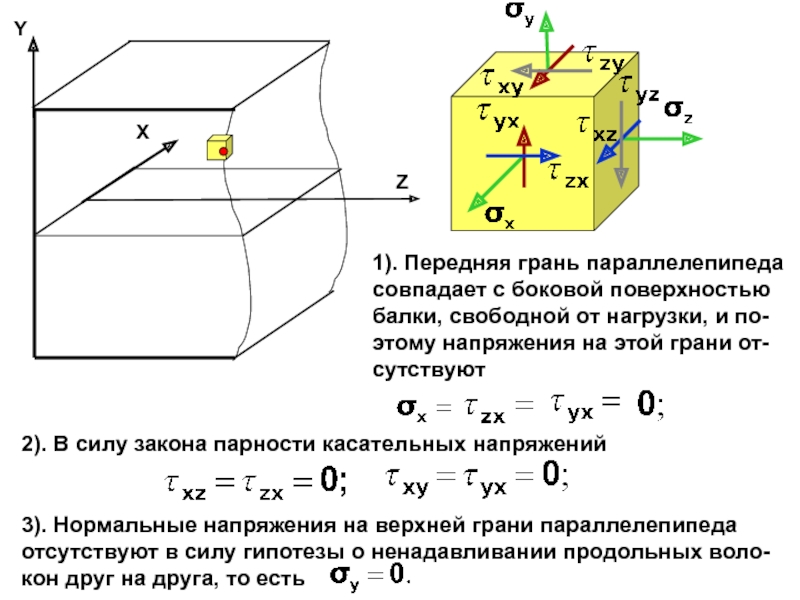
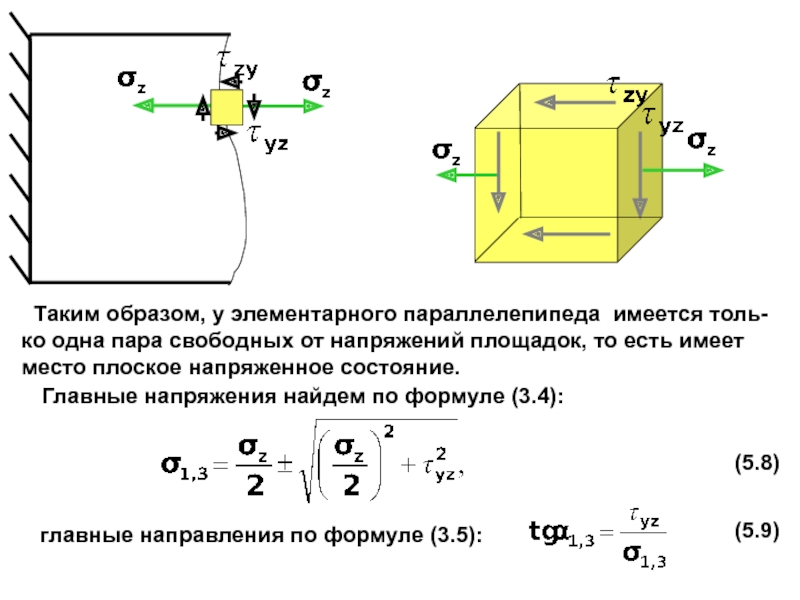
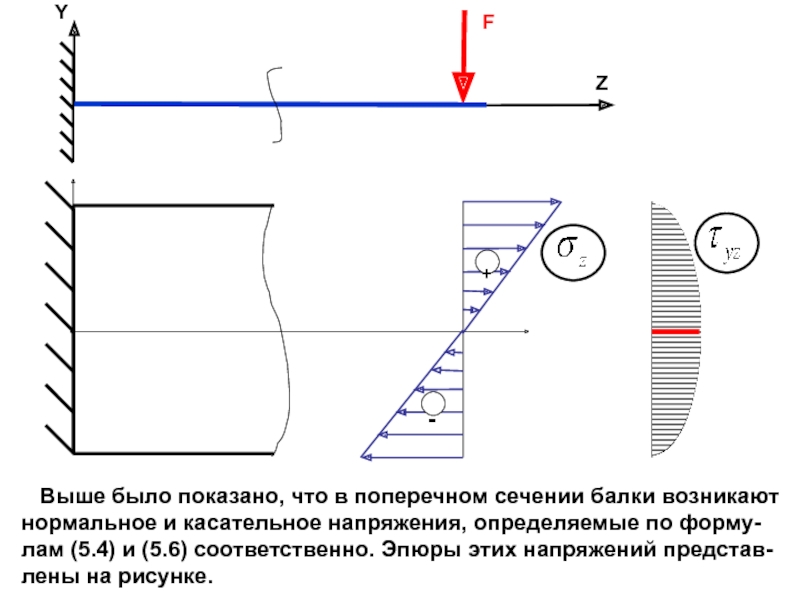
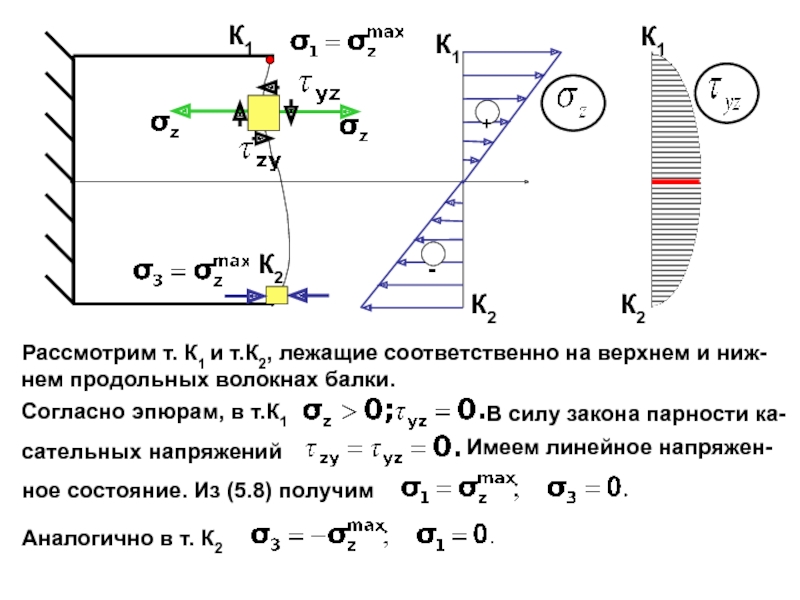
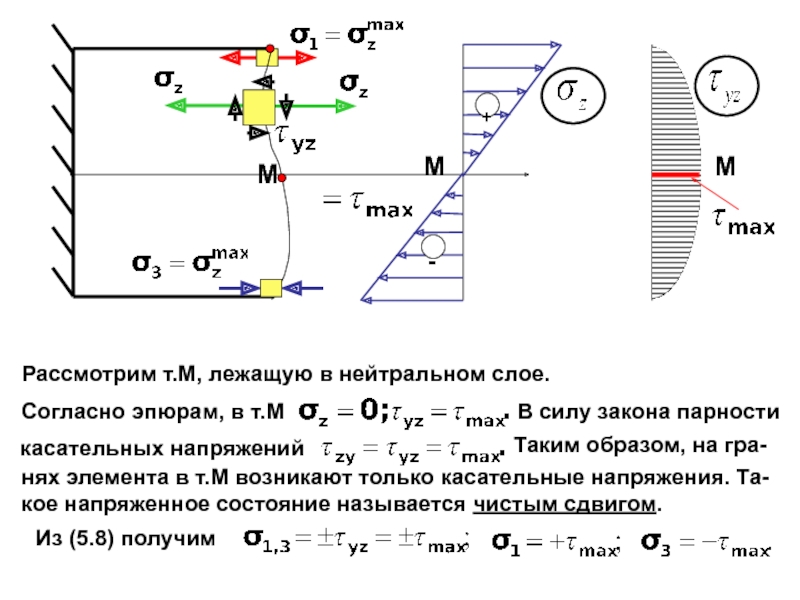
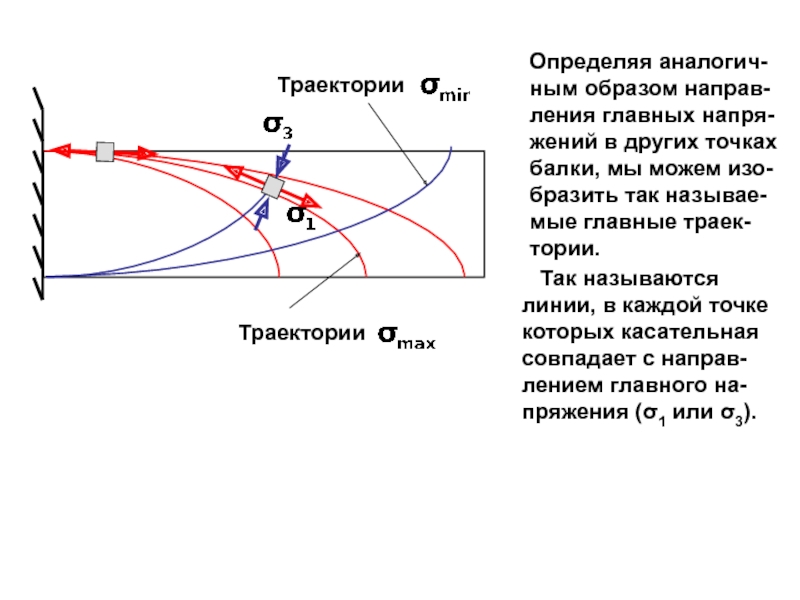
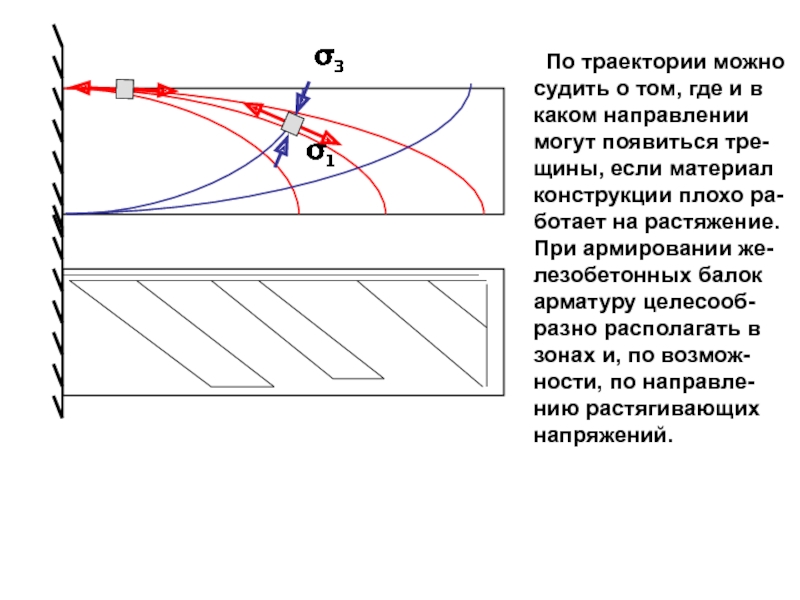
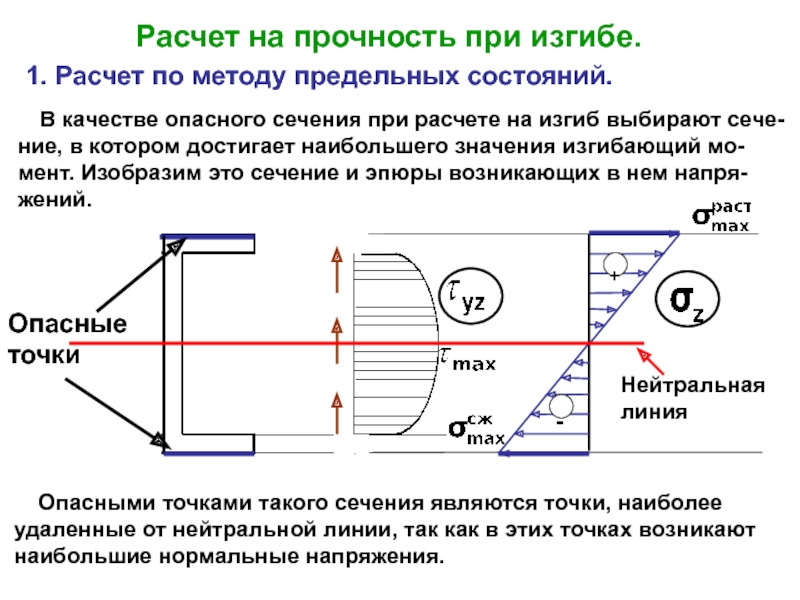
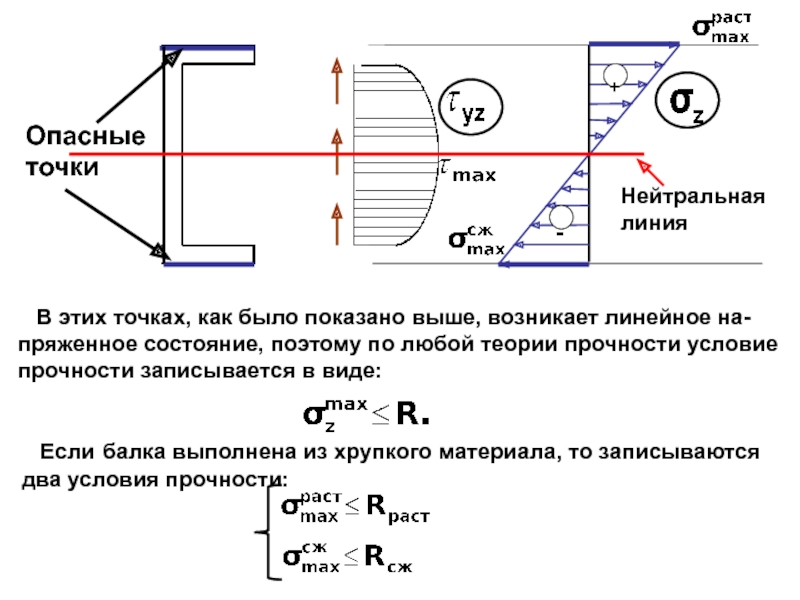
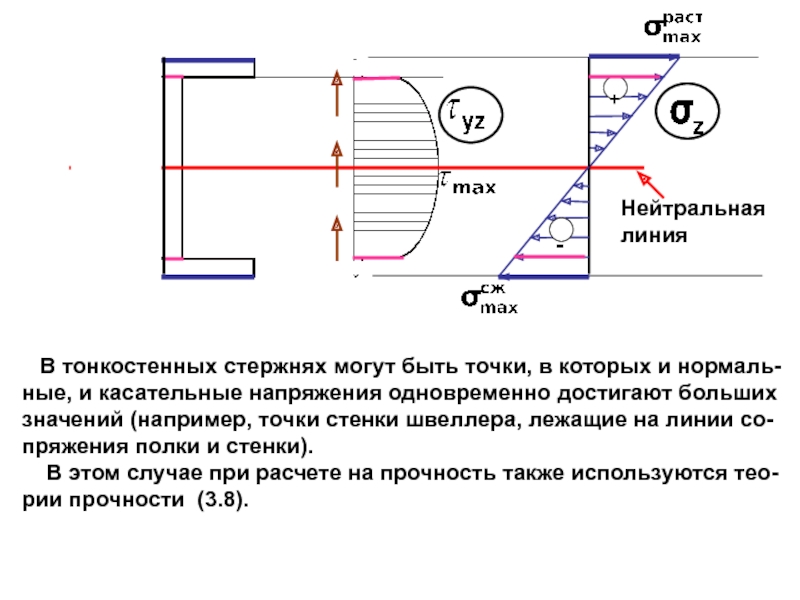
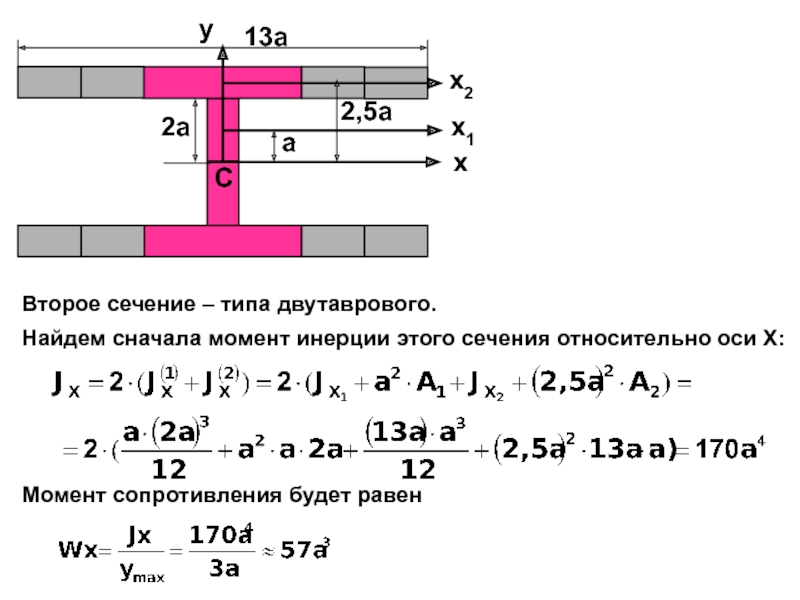
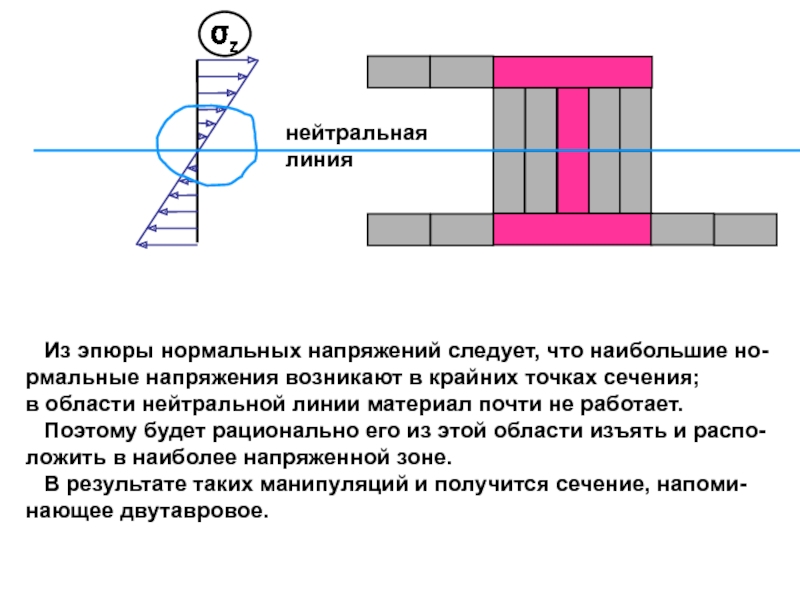
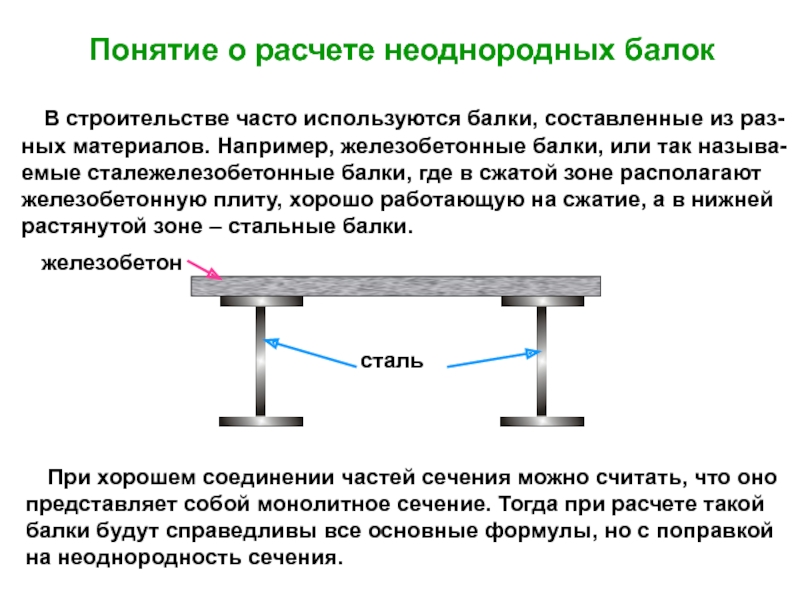
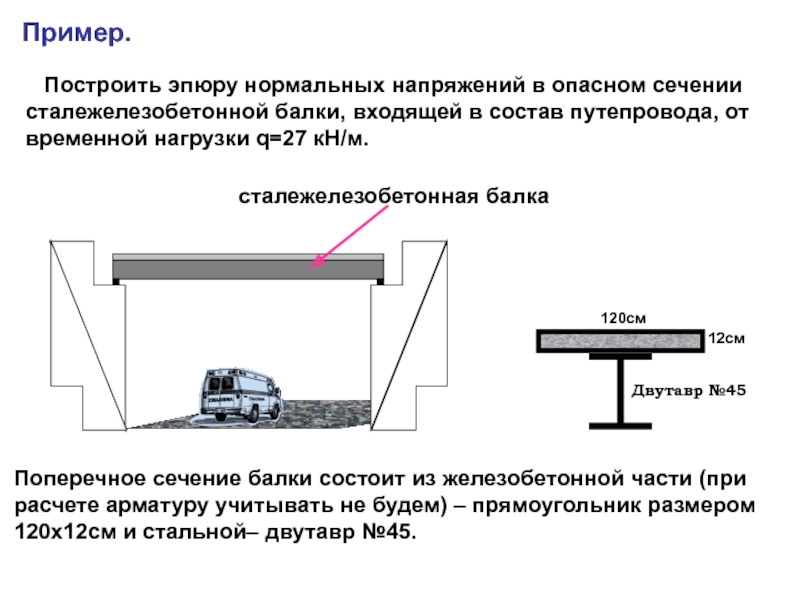
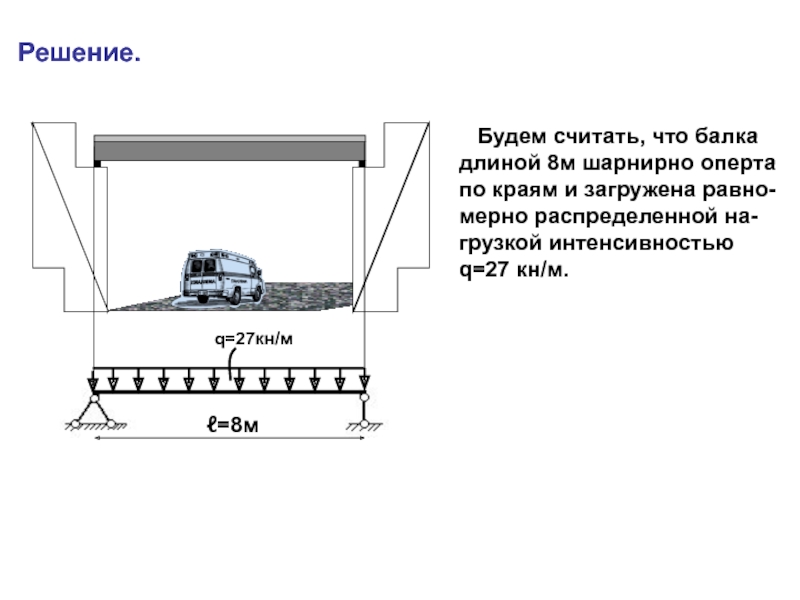
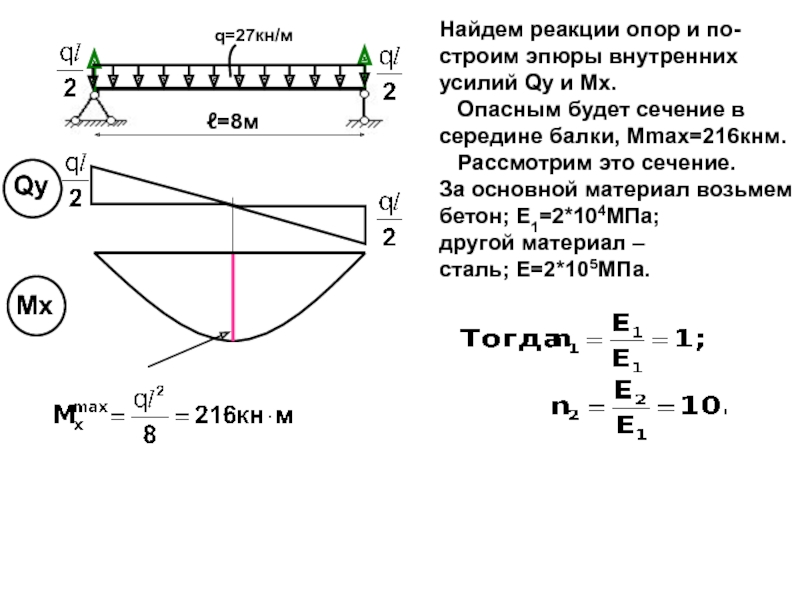
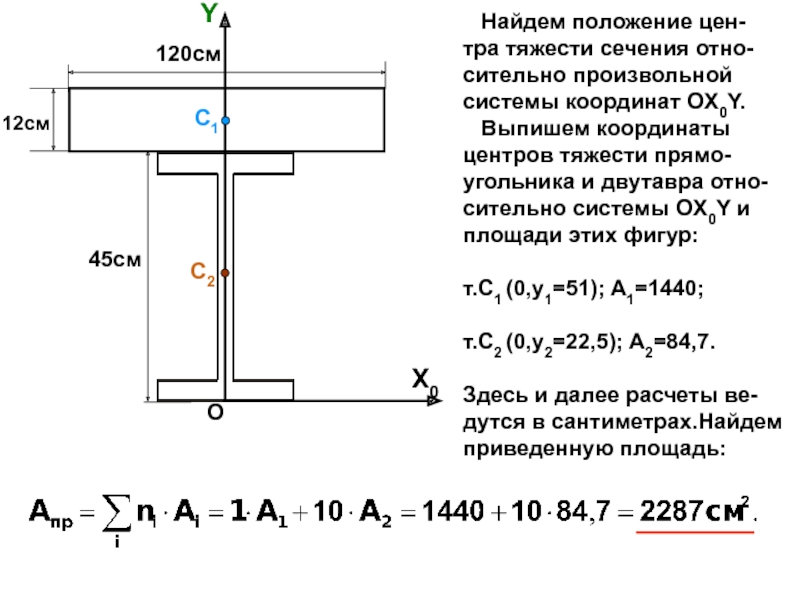
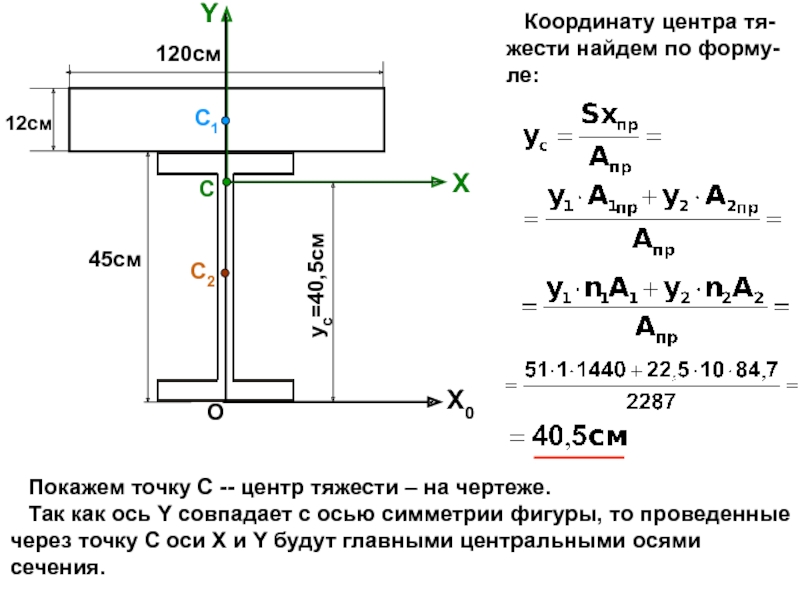
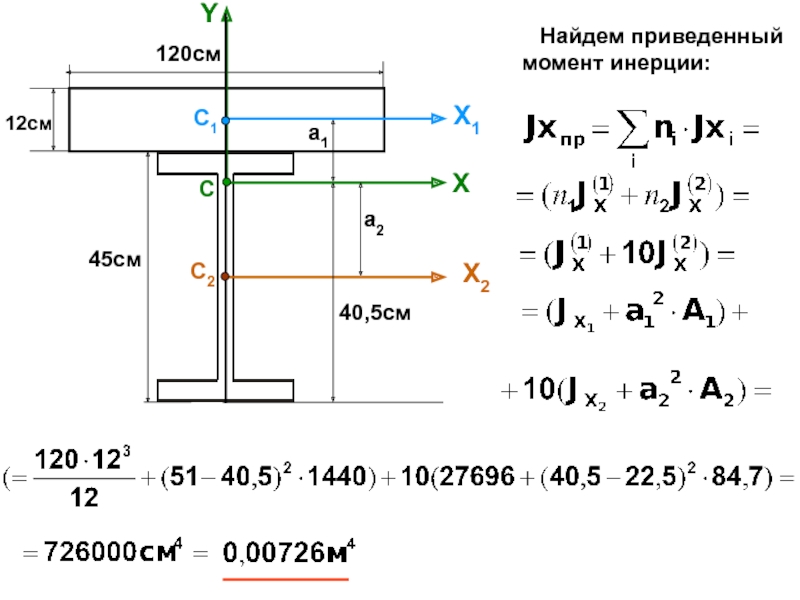
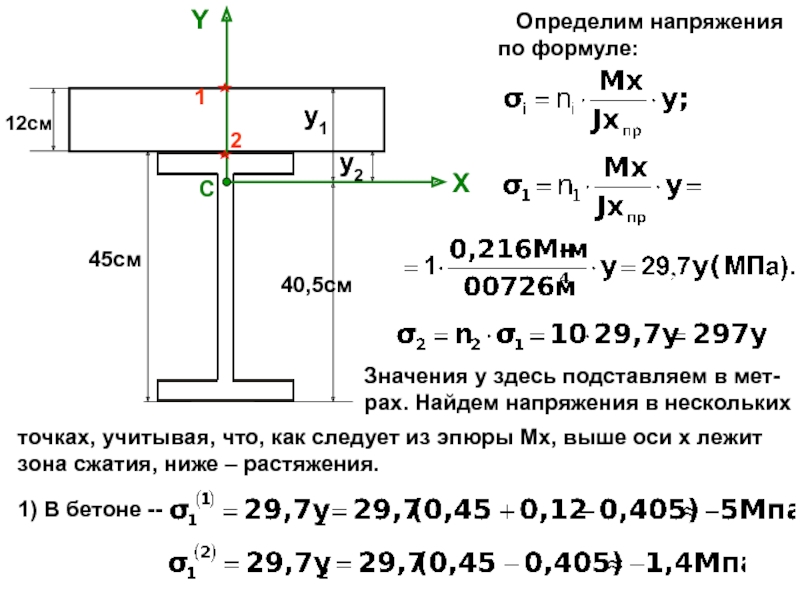
случаях:
1) если балка короткая;
2) если она нагружена большими сосредоточенными силами,
приложенными на малых расстояниях от опор. В таких бал-
ках поперечные силы могут иметь значительную величину,
в то время, как изгибающие моменты оказываются сравни-
тельно небольшими;
3) если балка деревянная. Для деревянных балок расчет на
прочность по касательным напряжениям может иметь реша-
ющее значение, так как дерево плохо сопротивляется ска-
лыванию вдоль волокон.
Условие прочности в точках, лежащих на нейтральной линии (ус-
ловие прочности по касательным напряжениям), проверяют, если
поперечная сила достигает наибольшего значения в опасном сече-нии балки.
Отметим, что точно также будет записываться условие прочности
во всех случаях состояния чистого сдвига.