- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Расчет криволинейных стержней презентация
Содержание
- 1. Расчет криволинейных стержней
- 2. Интеграл Мора можно использовать для определения перемещений
- 3. Пример: Для кривого бруса в форме четверти
- 4. Изгибающий момент от внешних сил
- 5. Задана плоская рама, состоящая из двух прямолинейных
- 6. Основная система Эквивалентная система 1 2 3
- 7. При расчете интегралов Мора будем учитывать только
- 8. F x2 Во втором стержне момент будет
- 9. x3 x1 F M0 q x2
- 10. x3 x1 X1=1 x2
- 11. x3 x1 X2=1 x2
- 12. x3 x1 X3=1 x2 От единичной
- 13. Система канонических уравнений метода сил для три
- 15. Решаем систему уравнений методом обращения матрицы Рассчитываем действительные значения внутренних силовых факторов (изгибающего момента)
- 16. Проверка правильности решения Сущность проверки правильности решения
- 17. x3 x1 X1=1 x2 От единичной
- 18. x3 x1 X2=1 x2 От единичной
- 19. x3 x1 X3=1 x2 От единичной
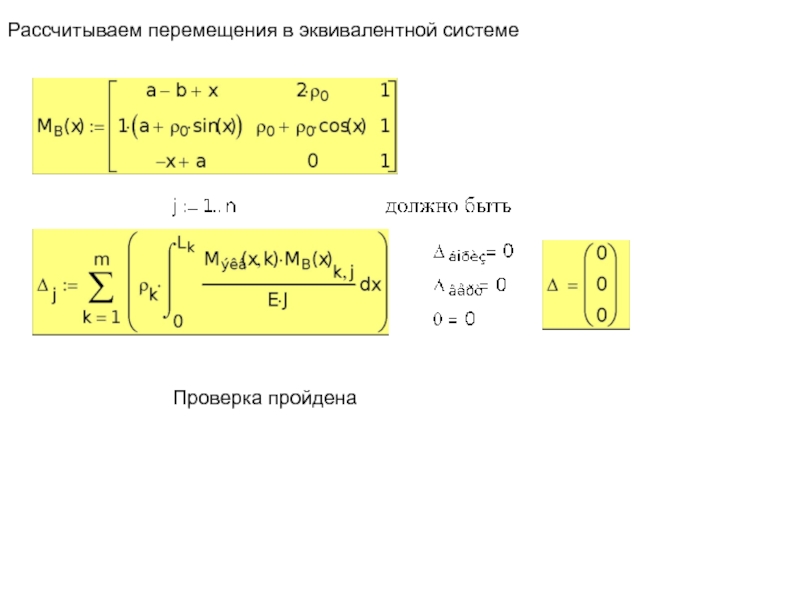
- 20. Рассчитываем перемещения в эквивалентной системе Проверка пройдена
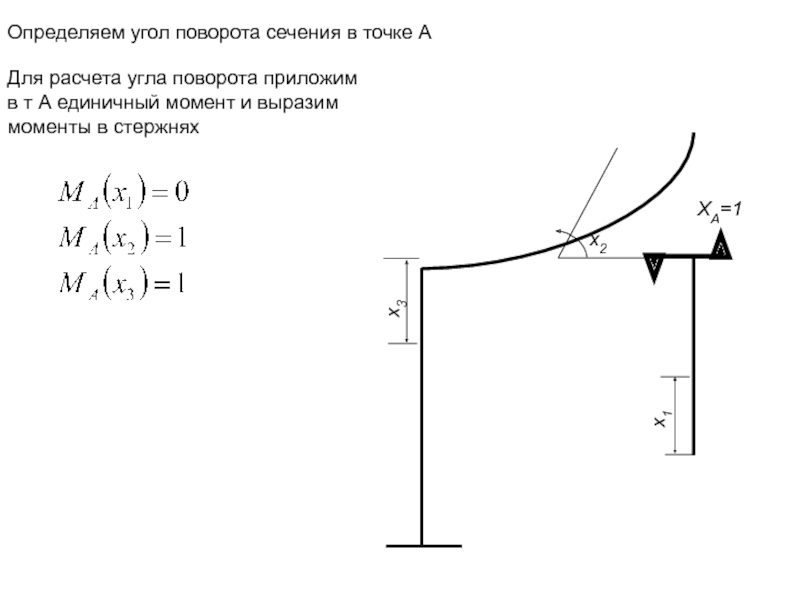
- 21. Определяем угол поворота сечения в точке А
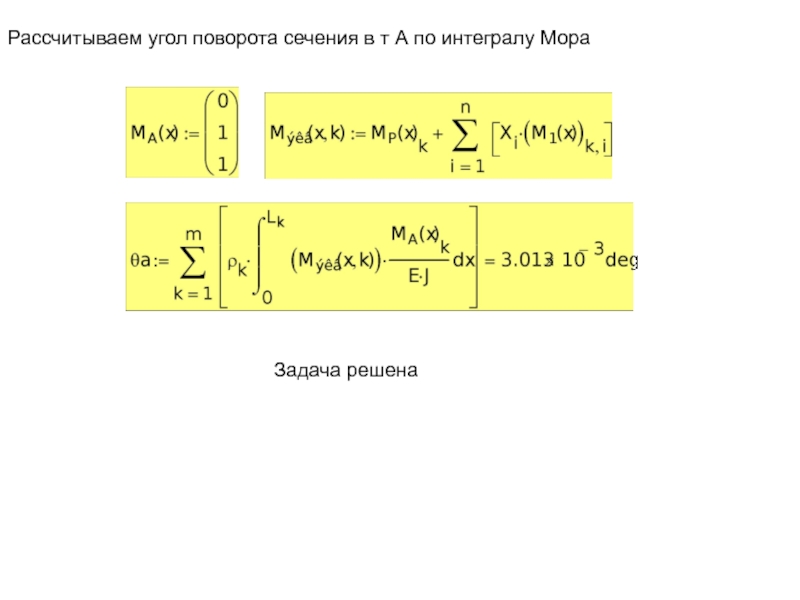
- 22. Рассчитываем угол поворота сечения в т А по интегралу Мора Задача решена
Слайд 2Интеграл Мора можно использовать для определения перемещений как прямолинейных, так и
Поскольку интеграл Мора вычисляется по длине, для криволинейных стержней вместо dx в подынтегральном выражении используется элемент длины дуги ds=ρdφ
где ρ - радиус кривизны стержня, который может быть постоянным, а может быть функцией от угловой координаты φ.
ρ
φ2
ds
dφ
φ1
φ
Слайд 3Пример:
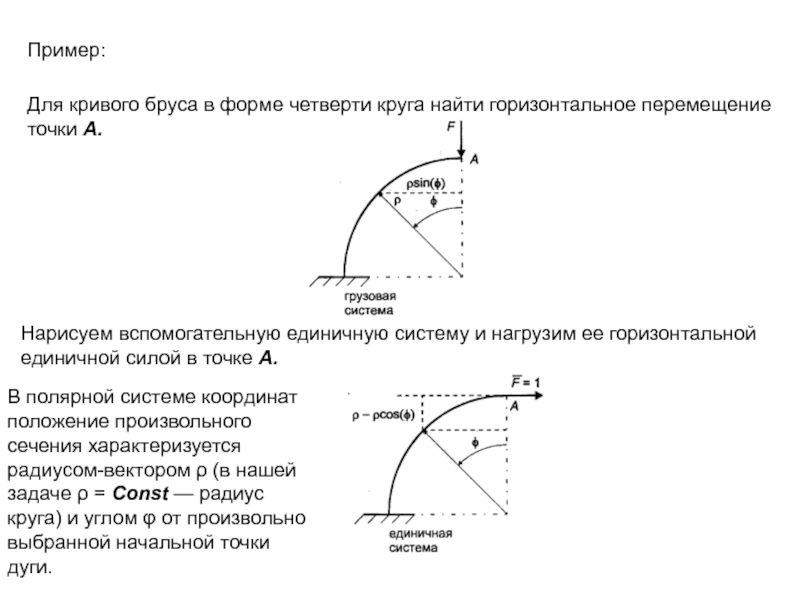
Для кривого бруса в форме четверти круга найти горизонтальное перемещение точки
Нарисуем вспомогательную единичную систему и нагрузим ее горизонтальной единичной силой в точке А.
В полярной системе координат положение произвольного сечения характеризуется радиусом-вектором ρ (в нашей задаче ρ = Const — радиус круга) и углом φ от произвольно выбранной начальной точки дуги.
Слайд 4Изгибающий момент от внешних сил
Изгибающий момент от единичной силы
Горизонтальное
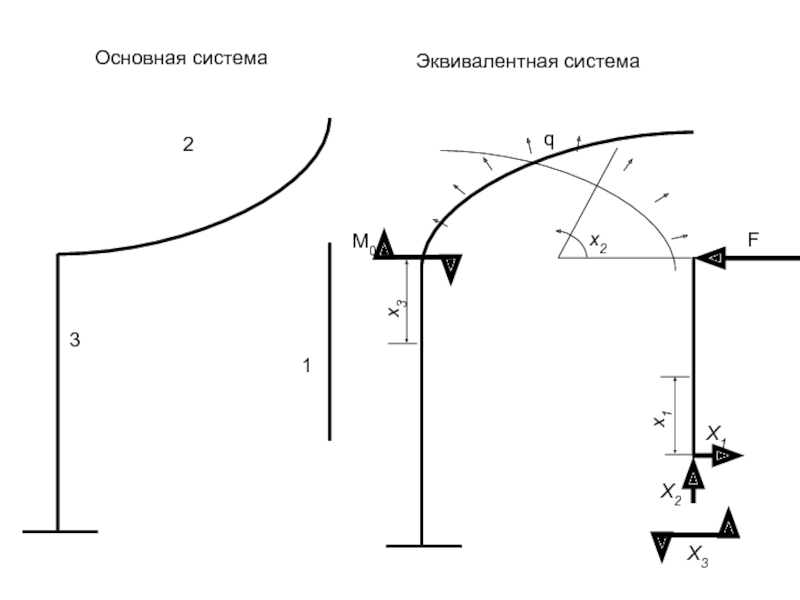
Слайд 5Задана плоская рама, состоящая из двух прямолинейных и одного криволинейного участка.
Система
На систему действуют сосредоточенная сила F, сосредоточенный момент M0, и распределенная нагрузка интенсивностью q.
Определить значения силовых факторов, действующих в стержнях, определить поворот сечения в точке А.
А
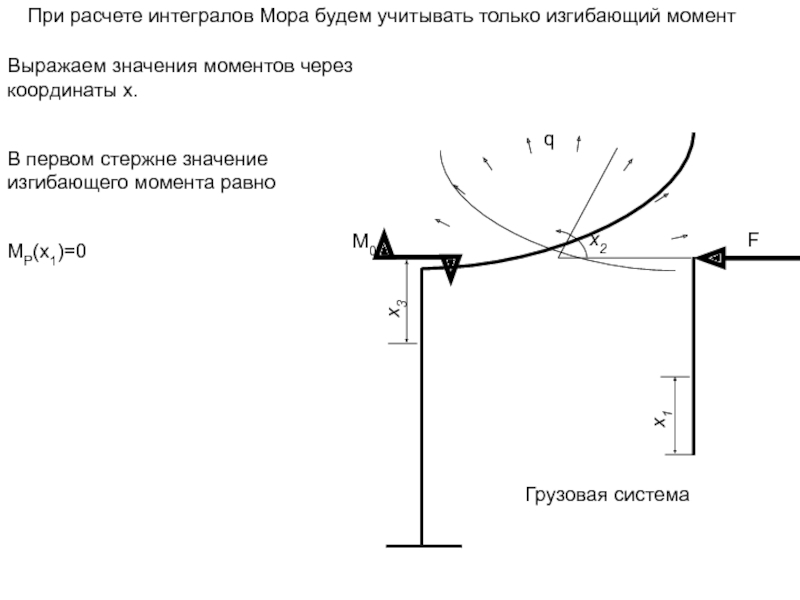
Слайд 7При расчете интегралов Мора будем учитывать только изгибающий момент
Выражаем значения моментов
В первом стержне значение изгибающего момента равнo
MP(x1)=0
x3
x1
F
M0
q
x2
Грузовая система
Слайд 8F
x2
Во втором стержне момент будет складываться из момента от силы F
q
x2
В сечении с координатой x2 момент от силы F будет равен
ds=ρdx
x
Момент от распределенной нагрузки может быть получен суммированием элементарных моментов, действующих на элементарный участок стержня ds=ρdx
В сечении с координатой x2 момент от распределенной нагрузки интенсивностью q будет равен интегралу
Суммарный момент
Слайд 9
x3
x1
F
M0
q
x2
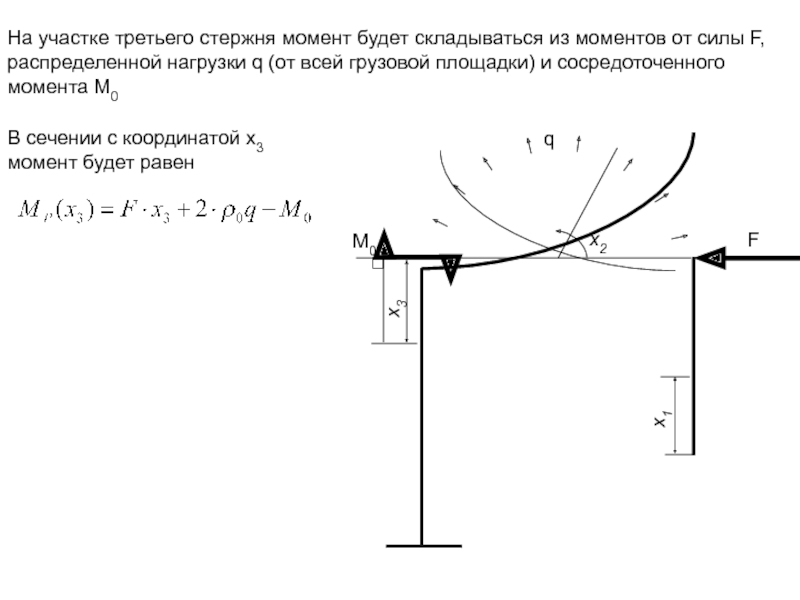
На участке третьего стержня момент будет складываться из моментов от силы
В сечении с координатой x3 момент будет равен
Слайд 10
x3
x1
X1=1
x2
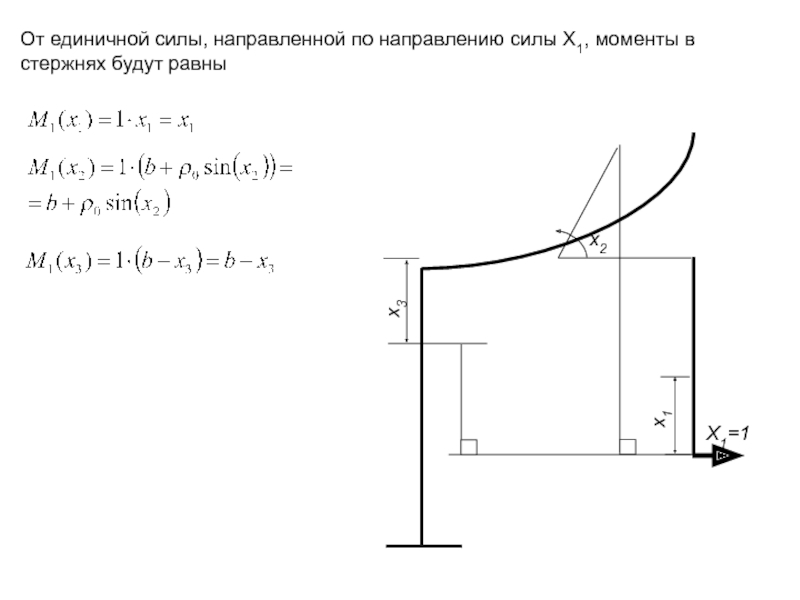
От единичной силы, направленной по направлению силы X1, моменты в стержнях
Слайд 11
x3
x1
X2=1
x2
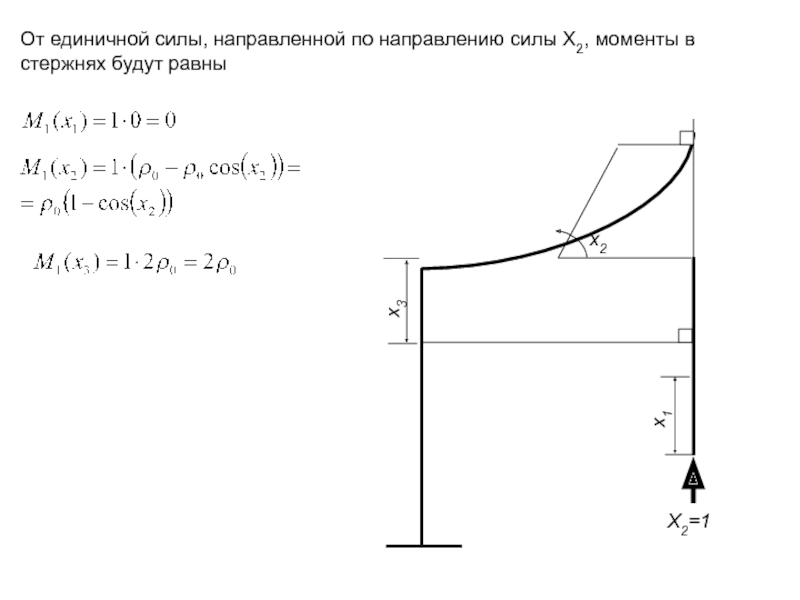
От единичной силы, направленной по направлению силы X2, моменты в стержнях
Слайд 12
x3
x1
X3=1
x2
От единичной силы, направленной по направлению силы X1, моменты в стержнях
Слайд 13Система канонических уравнений метода сил для три раза статически неопределимой системы
Для более компактного вида и удобства обработки систему можно представить в матричном виде
Величины δij и δ iP расчитываются как интегралы Мора между соответствующими моментами
Слайд 15Решаем систему уравнений методом обращения матрицы
Рассчитываем действительные значения внутренних силовых факторов
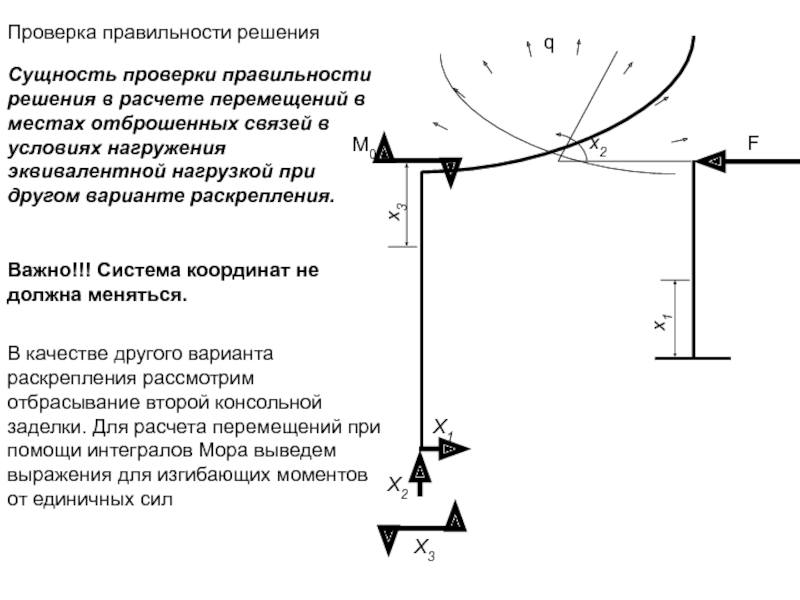
Слайд 16Проверка правильности решения
Сущность проверки правильности решения в расчете перемещений в местах
x3
x1
F
M0
q
X2
X1
X3
x2
Важно!!! Система координат не должна меняться.
В качестве другого варианта раскрепления рассмотрим отбрасывание второй консольной заделки. Для расчета перемещений при помощи интегралов Мора выведем выражения для изгибающих моментов от единичных сил
Слайд 17
x3
x1
X1=1
x2
От единичной силы, направленной по направлению силы X1, моменты в стержнях
Слайд 18
x3
x1
X2=1
x2
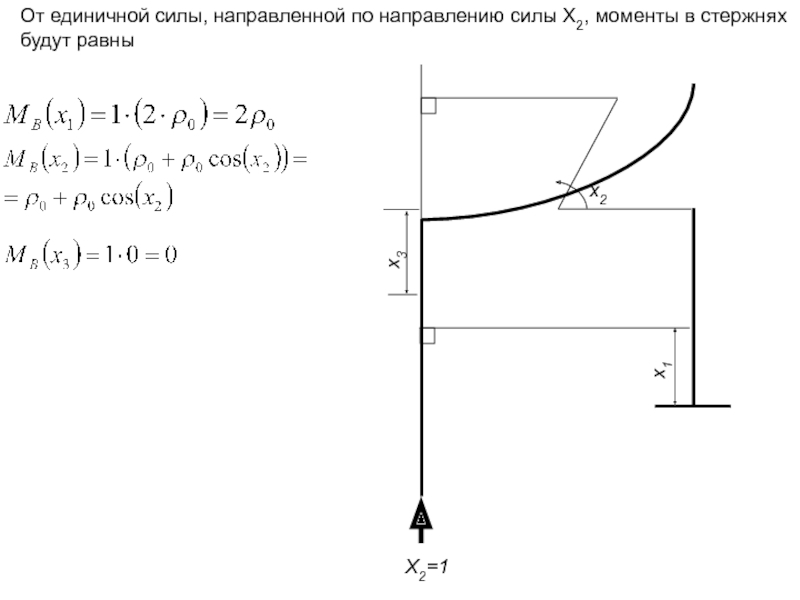
От единичной силы, направленной по направлению силы X2, моменты в стержнях
Слайд 19
x3
x1
X3=1
x2
От единичной силы, направленной по направлению силы X3, моменты в стержнях
Слайд 21Определяем угол поворота сечения в точке А
Для расчета угла поворота приложим
x3
x1
XА=1
x2