- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы описания дискретных систем презентация
Содержание
- 1. Методы описания дискретных систем
- 2. 1. Описание непрерывных систем
- 3. Описание непрерывных систем во временной области. Моделирование
- 4. Уравнения электрической цепи первого порядка Уравнения цепи (1) (2) (3) (4) (5)
- 5. Решение уравнения электрической цепи первого порядка
- 6. Дискретизация уравнения цепи первого порядка для моделирования
- 7. Преобразуем уравнение (12): Дискретизация уравнения цепи первого порядка для моделирования на ЭВМ
- 8. Дискретизация уравнения цепи первого порядка для моделирования
- 9. Описание дискретных систем в частотной области
- 10. Описание дискретных систем в частотной области
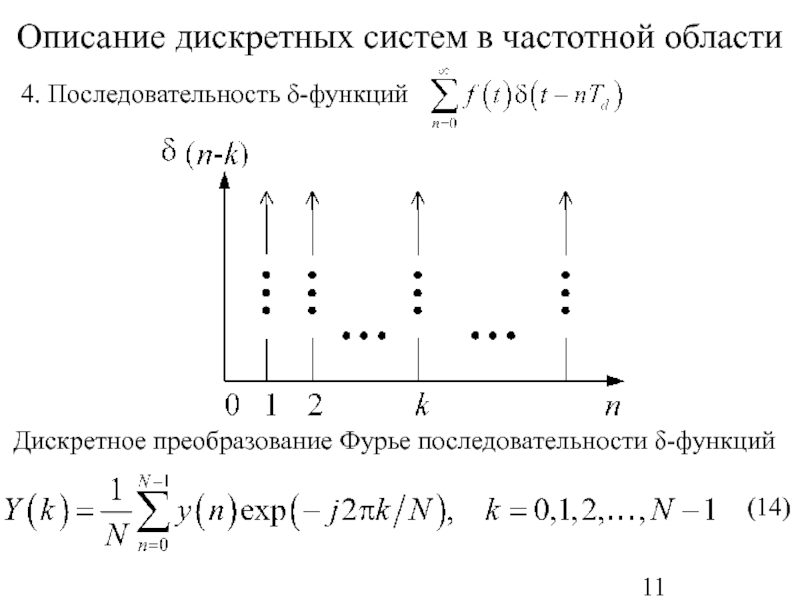
- 11. Описание дискретных систем в частотной области Дискретное преобразование Фурье последовательности δ-функций
- 12. Описание дискретных систем в частотной области Тогда 5. Дискретное преобразование Лапласа
- 13. Описание дискретных систем в частотной области
- 14. Описание дискретных систем в частотной области
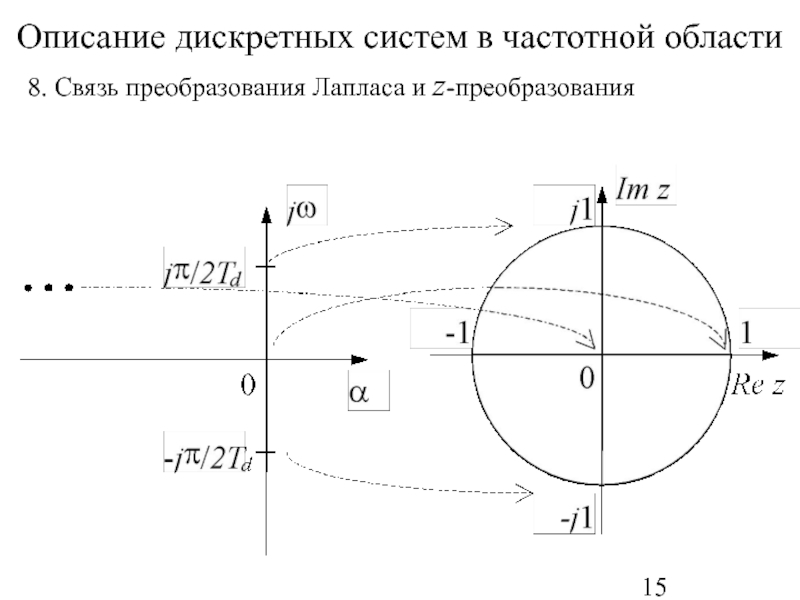
- 15. Описание дискретных систем в частотной области 8. Связь преобразования Лапласа и z-преобразования
- 16. Описание дискретных систем в частотной области
- 17. Описание дискретных систем в частотной области
- 18. Описание дискретных систем в частотной области 11. z-преобразование дробно-рациональной функции 5-го порядка
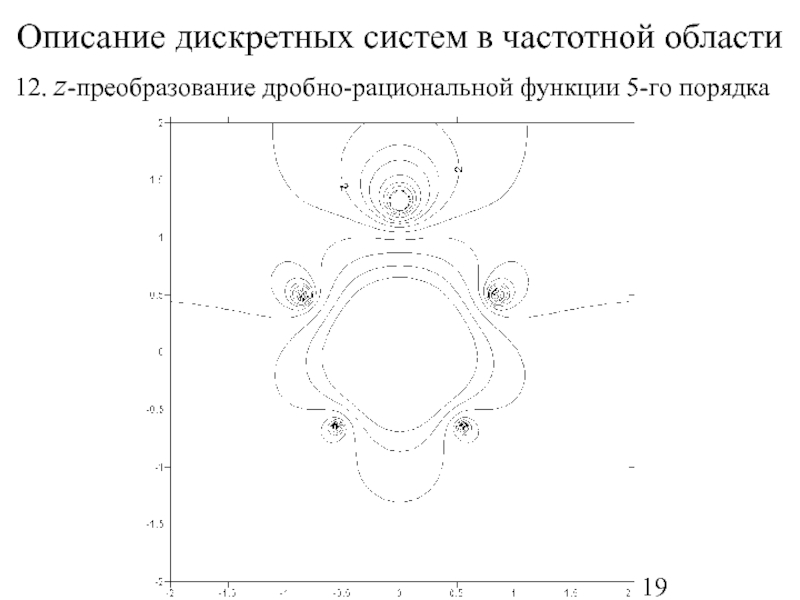
- 19. Описание дискретных систем в частотной области 12. z-преобразование дробно-рациональной функции 5-го порядка
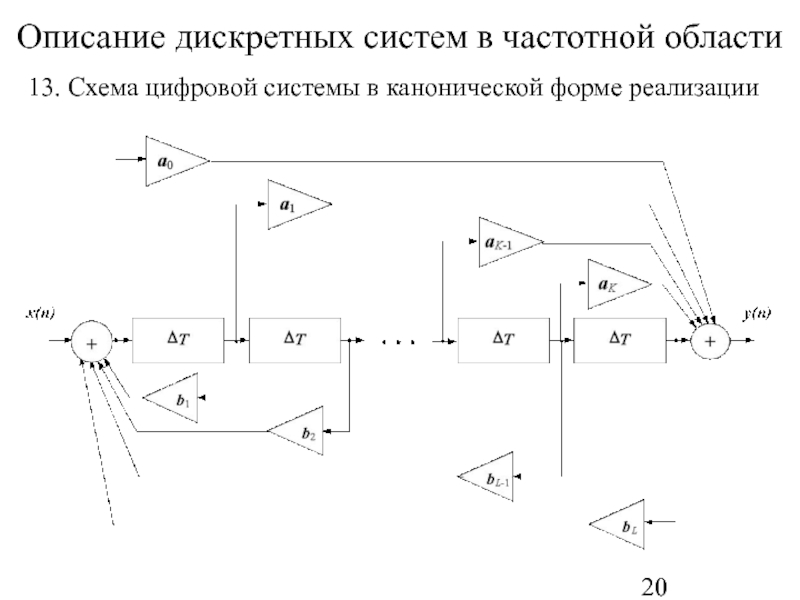
- 20. Описание дискретных систем в частотной области
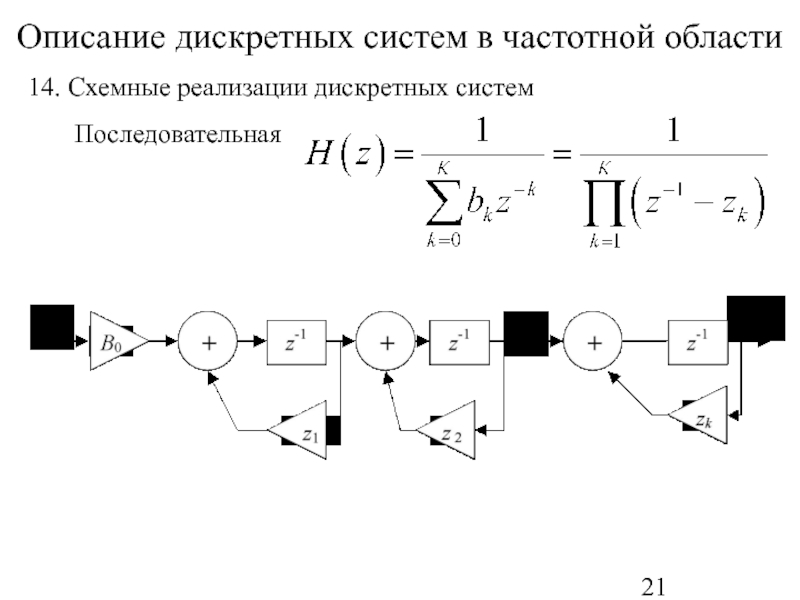
- 21. Описание дискретных систем в частотной области 14. Схемные реализации дискретных систем Последовательная
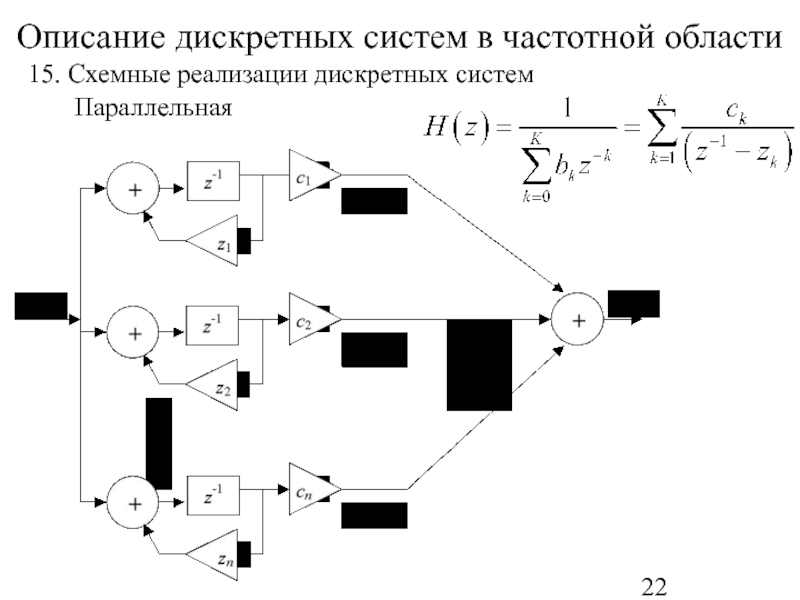
- 22. Описание дискретных систем в частотной области 15. Схемные реализации дискретных систем Параллельная
- 23. Применение метода пространства состояний для описания сложных
- 24. Применение метода пространства состояний для описания сложных
- 25. Применение метода пространства состояний для описания сложных
- 26. Применение метода пространства состояний для описания сложных
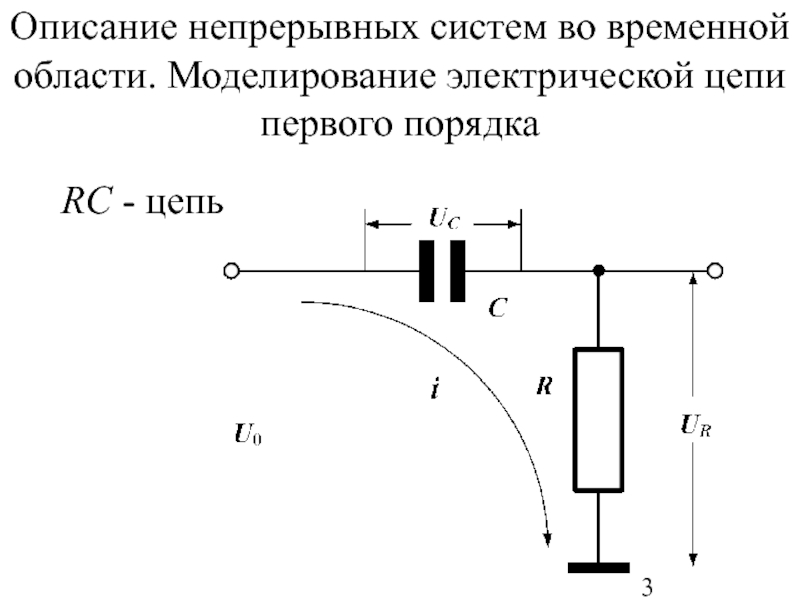
Слайд 3Описание непрерывных систем во временной области. Моделирование электрической цепи первого порядка
RC - цепь
Слайд 5Решение уравнения электрической цепи первого порядка
Уравнение (5) является неоднородным линейным
(6),
(7)
(8)
т.е.
Общее решение уравнения (6)
(9)
где A1 - произвольная постоянная интегрирования.
Окончательное решение
(10)
Слайд 6Дискретизация уравнения цепи первого порядка для моделирования на ЭВМ
Замена производной
(11)
Замена непрерывного времени дискретным: t → n
(12)
Слайд 7Преобразуем уравнение (12):
Дискретизация уравнения цепи первого порядка для моделирования на
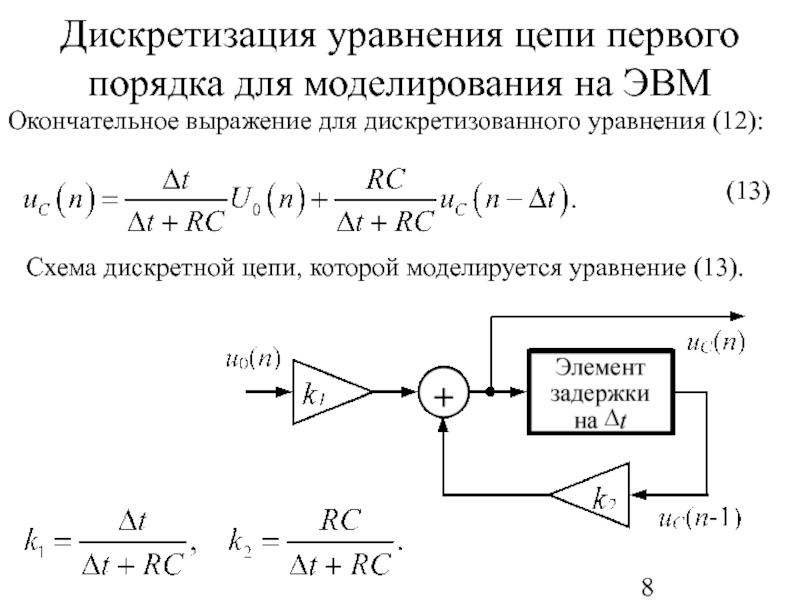
Слайд 8Дискретизация уравнения цепи первого порядка для моделирования на ЭВМ
Окончательное выражение
(13)
Схема дискретной цепи, которой моделируется уравнение (13).
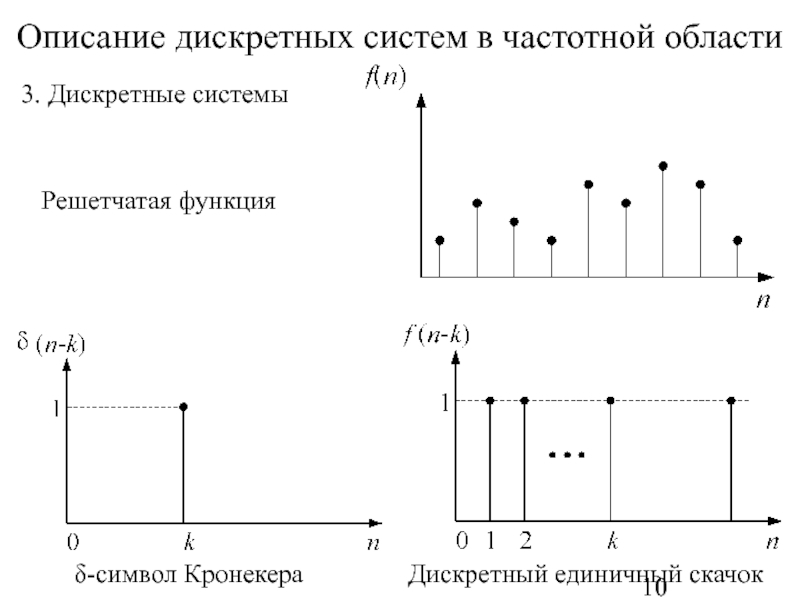
Слайд 10Описание дискретных систем в частотной области
Решетчатая функция
δ-символ Кронекера
Дискретный единичный скачок
3.
Слайд 11Описание дискретных систем в частотной области
Дискретное преобразование Фурье последовательности δ-функций
Слайд 13Описание дискретных систем в частотной области
Тогда, с учетом (15)
Выражения (15)
6. Пример
Слайд 14Описание дискретных систем в частотной области
Тогда выражение (5) преобразуется к
, (17)
(19)
Слайд 15Описание дискретных систем в частотной области
8. Связь преобразования Лапласа и
Слайд 18Описание дискретных систем в частотной области
11. z-преобразование дробно-рациональной функции 5-го
Слайд 19Описание дискретных систем в частотной области
12. z-преобразование дробно-рациональной функции 5-го
Слайд 20Описание дискретных систем в частотной области
13. Схема цифровой системы в
Слайд 21Описание дискретных систем в частотной области
14. Схемные реализации дискретных систем
Последовательная
Слайд 22Описание дискретных систем в частотной области
15. Схемные реализации дискретных систем
Параллельная
Слайд 23Применение метода пространства состояний для описания сложных систем
Определим состояние системы как
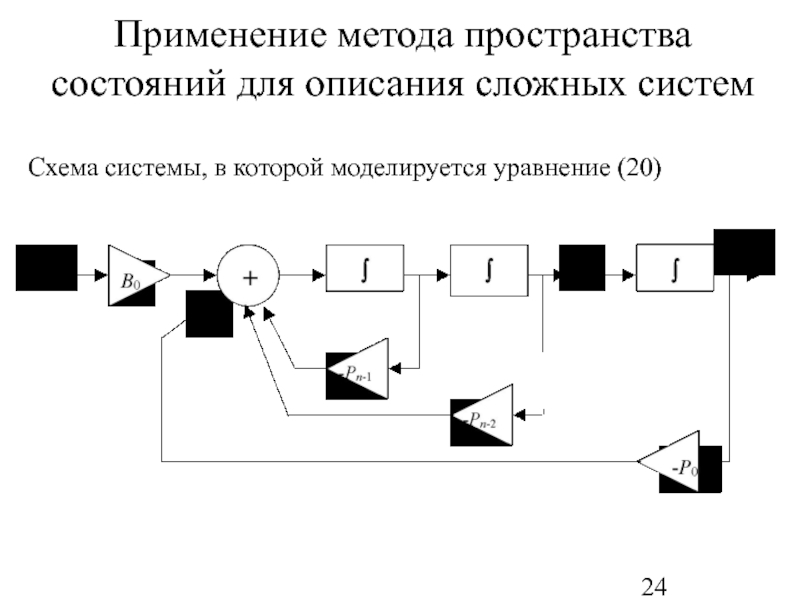
Рассмотрим общий метод описания сложной динамической системы в терминах переменных состояния. Пусть система описывается дифференциальным уравнением вида:
(20)
где – n-я производная от ; – коэффициенты,
зависящие от времени; – зависящий от времени коэффициент усиления входного сигнала U(t).
Слайд 24Применение метода пространства состояний для описания сложных систем
Схема системы, в
Слайд 25Применение метода пространства состояний для описания сложных систем
Векторное представление уравнения
(20а)
(20б)
или
Слайд 26Применение метода пространства состояний для описания сложных систем
(21)
Представим набор переменных
где