Проводники в электростатическом поле презентация

Вещества, у которых под действием электрического поля преобладающим является процесс неограниченного движения зарядов, называются проводниками.

У концов проводника собираются заряды противоположного знака

Это индуцированные заряды. Процесс их возникновения называется электростатической индукцией.

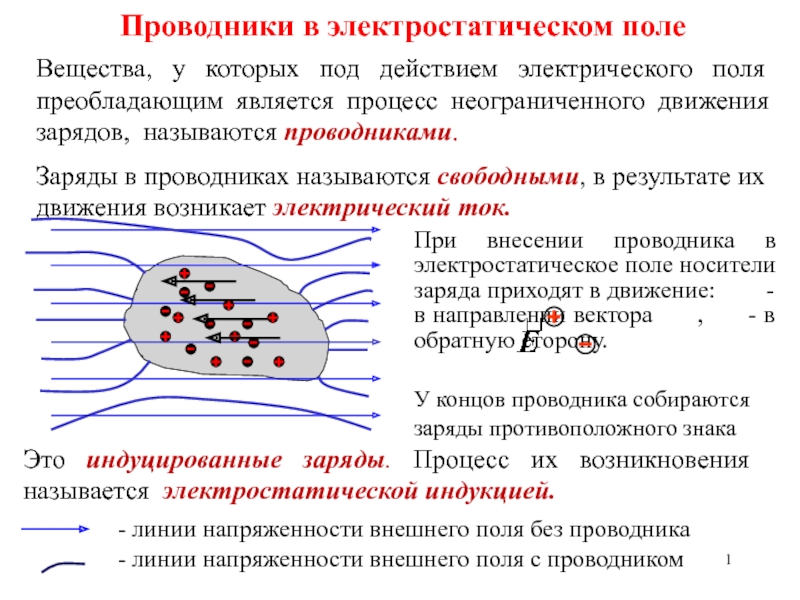
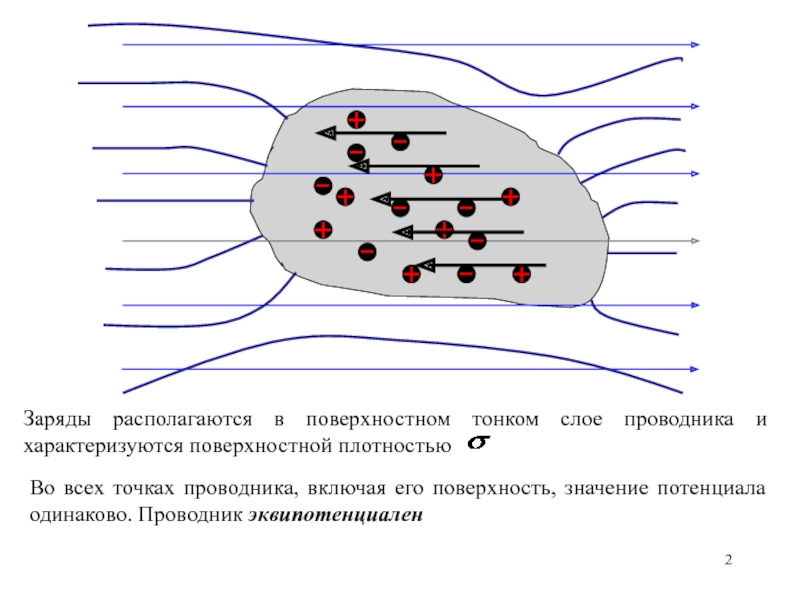
Напряжённость поля вблизи поверхности заряженного проводника прямо пропорциональна поверхностной плотности зарядов.

Электроемкость уединенного проводника

Различные по величине заряды распределяются на уединённом проводнике подобным образом (отношение плотностей заряда в двух произвольных точках поверхности проводника при любом заряде будет одним и тем же).

Коэффициент пропорциональности между потенциалом и зарядом называется электроёмкостью

Ёмкость численно равна заряду, сообщение которого проводнику вызывает повышение его потенциала на единицу.

Единица электроемкости – фарад.

Например, две пластинки, два коаксиальных цилиндра или две концентрические сферы, расположенные близко друг к другу.

U – напряжение между обкладками

Найдём формулу для ёмкости плоского конденсатора.

S – площадь обкладки, q – заряд конденсатора

Энергия заряженного конденсатора

U' – мгновенное значение напряжения на обкладках конденсатора

q = C⋅U

Сила тока есть величина, равная заряду, переносимому через поперечное сечение проводника в единицу времени.

Для протекания электрического тока необходимы два условия.
Наличие частиц, которые могут свободно перемещаться в пределах проводящей среды (носителей заряда).
Электрическое поле внутри среды.

Зная плотность тока можно найти ток.

Через сечение dS за время dt пройдут только те электроны, которые находятся в объёме dV = dS ⋅v⋅dt.
Тогда за dt через dS пройдёт заряд.
dq = en⋅v⋅dS⋅dt. n – концентрация электронов.

ρ - объёмная плотность заряда

Представим:

Тогда:

Для кругооборота зарядов должна быть совершена работа против сил электрического поля.

Такая работа может совершаться только за счет сил, имеющих не электростатическую природу.

Силы, поддерживающие постоянный электрический ток, называются сторонними электродвижущими силами (ЭДС)

Электродвижущая сила (ЭДС) измеряется работой, совершаемой сторонними силами источника по перемещению единичного положительного заряда внутри источника от отрицательного полюса к положительному.

Величина, численно равная работе по переносу единичного положительного заряда суммарным полем кулоновских и сторонних сил на участке цепи (1–2), называется напряжением на этом участке цепи (U12).

Это выражение представляет собой обобщённый закон Ома.

Для однородного проводника

ρ – удельное сопротивление, измеряемое в Ом⋅м. l и S – длина и площадь поперечного сечения проводника.

Закон Ома в дифференциальной форме:

Сверхпроводимость материалов: у большой группы металлов и сплавов при температурах, близких к нулю , удельное сопротивление скачком обращается в нуль.

При этом силы электростатического поля и сторонние силы на этом участке совершают работу

Разделим работу на время и получим выражение для мощности.

Мощность может расходоваться на совершение работы над внешними телами, на нагрев участка проводника и т.д.

Удельная тепловая мощность тока пропорциональна квадрату плотности электрического тока и удельному сопротивлению среды в данной точке.

Относится к узлам цепи, т.е. точкам разветвления цепи.
Алгебраическая сумма токов, сходящихся в узле, равна нулю.

N – число рассматриваемых участков выбранного контура

ЭДС положительна, если при обходе контура совершается переход внутри источника от отрицательного полюса к положительному