- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Механические колебания и волны презентация
Содержание
- 1. Механические колебания и волны
- 2. Колебаниями называются процессы, отличающиеся той или иной
- 3. Т – период колебаний – минимальный промежуток
- 4. Рассмотрим систему, состоящую из шарика массы m,
- 5. Знак «—» в формуле отражает то обстоятельство,
- 6. Сообщим шарику смещение х =d, после чего
- 7. Любому колебательному процессу присуще: Наличие положения равновесия
- 8. Период колебаний пружинного маятника: График гармонического колебания
- 9. Скорость и ускорение гармонического колебания Смещение описывается
- 10. Видно, что ускорение и смещение находятся в
- 11. 2. Математический маятник l ϕ lsinϕ Математическим
- 12. Ограничимся рассмотрением малых колебаний Получим: Обозначим: Получим:
- 13. 3. Физический маятник Физическим маятником называется твердое
- 14. или где - период колебаний физического маятника
- 15. 4. Энергия гармонического колебания Квазиупругая сила является
- 17. Затухающие колебания Вынужденные колебания Автоколебания
- 18. 1. Затухающие колебания Затухающими называются колебания, энергия
- 19. Продифференцируем по t, найдем подставляя в получим:
- 20. I II I уравнение можно представить в
- 21. Произведя потенцирование, получим - зависимость амплитуды свободных
- 22. Скорость затухания колебаний определяется величиной которую называют
- 23. Отношение двух последующих амплитуд называют декрементом затухания:
- 24. 2. Вынужденные колебания Вынужденными называются колебания, возникающие
- 25. Общее решение однородного уравнения: Найдем частное
- 26. Из II уравнения: Возведем I и II уравнения в квадрат: Складываем уравнения: I II
- 27. Амплитуда вынужденных колебаний Т.о. частное решение: Общее
- 28. Установление колебаний Зависимость амплитуды вынужденных колебаний от
- 29. Продифференцировав подкоренное выражение по ω и приравняв
- 30. При β = 0 При β = 0 Резонансная кривая А
- 31. Автоколебания При затухающих колебаниях энергия системы
- 32. 1. Представление гармонических колебаний с помощью вращающегося
Слайд 1Механические колебания и волны
Гармонические колебания
Математический маятник
Физический маятник
Энергия гармонического колебания
Слайд 2Колебаниями называются процессы, отличающиеся той или иной степенью повторяемости.
Гармонические колебания
В
В зависимости от характера воздействия, оказываемого на колеблющуюся систему, различают свободные (или собственные) колебания, вынужденные колебания, автоколебания и параметрические колебания.
Свободными или собственными называются такие колебания, которые происходят в системе, предоставленной самой себе после того, как ей был сообщен толчок, либо она была выведена из положения равновесия.
Простейшими являются гармонические колебания, т. е. такие колебания, при которых колеблющаяся величина изменяется со временем по закону синуса или косинуса.
Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебаний, повторяются через равные промежутки времени.
Слайд 3Т – период колебаний – минимальный промежуток времени, по истечении которого
Частота колебаний ν определяется, как число полных колебаний в 1 секунду.
ω – циклическая (круговая) частота – число полных колебаний за 2π секунд.
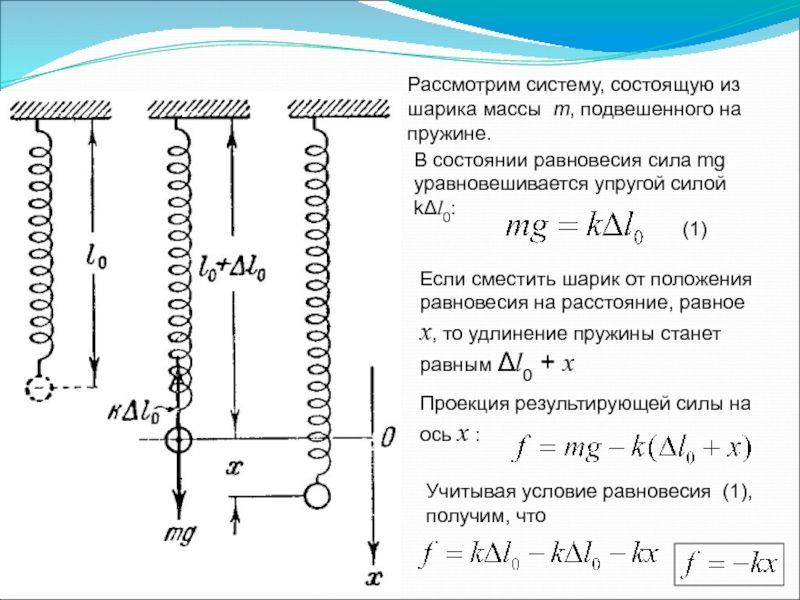
Слайд 4Рассмотрим систему, состоящую из шарика массы m, подвешенного на пружине.
В
Если сместить шарик от положения равновесия на расстояние, равное х, то удлинение пружины станет равным Δl0 + х
Проекция результирующей силы на ось х :
Учитывая условие равновесия (1), получим, что
(1)
Слайд 5Знак «—» в формуле отражает то обстоятельство, что смещение и сила
Таким образом, сила f обладает следующими свойствами: 1) она пропорциональна смещению шарика из положения равновесия, 2) она всегда направлена к положению равновесия.
Силы такого вида, независимо от их природы, принято называть квазиупругими.
Для того, чтобы сообщить системе смещение х, нужно совершить против квазиупругой силы работу :
Эта работа идет на создание запаса потенциальной энергии системы. Следовательно, система, в которой действует квазиупругая сила, при смещении из положения равновесия на расстояние х обладает потенциальной энергией:
Слайд 6Сообщим шарику смещение х =d, после чего предоставим систему самой себе.
При этом потенциальная энергия системы будет убывать , но зато появится все возрастающая кинетическая энергия (массой пружины пренебрегаем).
Придя в положение равновесия, шарик продолжает двигаться по инерции. Это движение будет замедленным и прекратится тогда, когда кинетическая энергия полностью превратится в потенциальную, т. е. когда смещение шарика станет равным - d. Затем такой же процесс будет протекать при движении шарика в обратном направлении.
Если трение в системе отсутствует, энергия системы должна сохраняться и шарик будет двигаться в пределах от х = d до х = - d.
Слайд 7Любому колебательному процессу присуще:
Наличие положения равновесия
Наличие возвращающей силы
Наличие инерции колеблющегося тела
Запишем
обозначим
уравнение колебаний шарика на пружине
Решение уравнения колебаний имеет вид:
или
Смещение х изменяется со временем по закону косинуса. Следовательно, движение системы, находящейся под действием силы вида f = —kx, представляет собой гармоническое колебание.
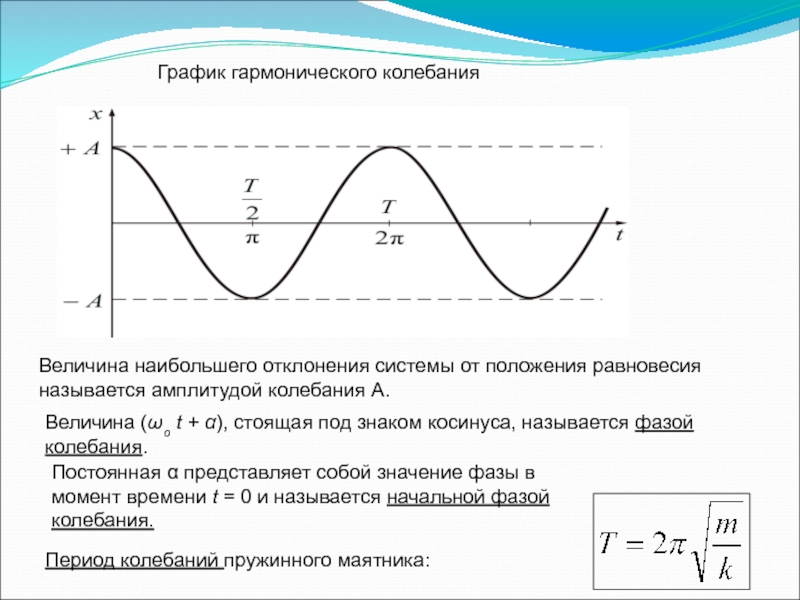
Слайд 8Период колебаний пружинного маятника:
График гармонического колебания
Величина наибольшего отклонения системы от
Величина (ωo t + α), стоящая под знаком косинуса, называется фазой колебания.
Постоянная α представляет собой значение фазы в момент времени t = 0 и называется начальной фазой колебания.
Слайд 9Скорость и ускорение гармонического колебания
Смещение описывается уравнением
Продифференцировав по времени выражение x(t), получим выражение для скорости
где
– амплитуда скорости;
Продифференцировав по времени выражение υ(t), получим выражение для ускорения
где
– амплитуда ускорения.
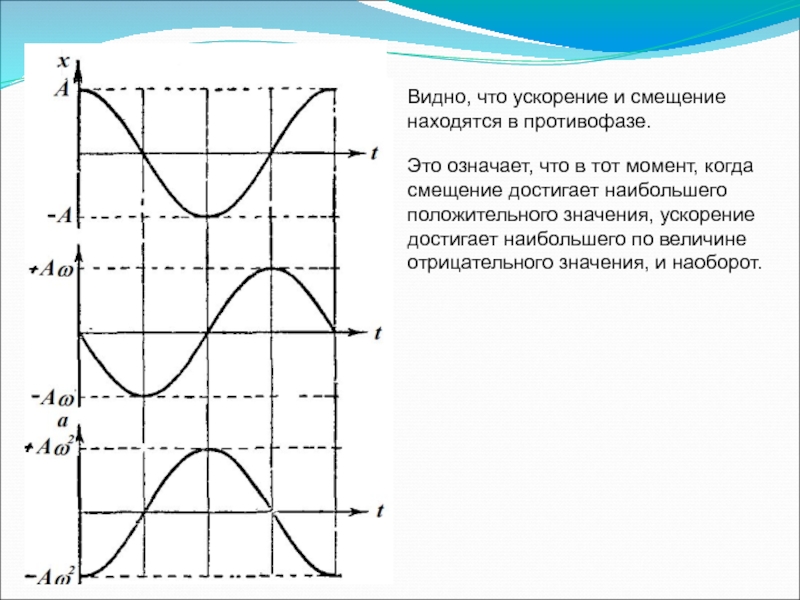
Слайд 10Видно, что ускорение и смещение находятся в противофазе.
Это означает, что
Слайд 112. Математический маятник
l
ϕ
lsinϕ
Математическим маятником называют идеализированную систему.
Математический маятник – материальная точка,
При отклонении маятника от положения равновесия возникает вращательный момент М.
Запишем для маятника уравнение динамики вращательного движения.
Учтем, что
Получим:
или
Слайд 12Ограничимся рассмотрением малых колебаний
Получим:
Обозначим:
Получим:
Решение этого уравнения имеет вид:
(гармонические колебания)
- частота колебаний
- период колебаний математического маятника
Слайд 133. Физический маятник
Физическим маятником называется твердое тело, способное совершать колебания вокруг
При отклонении маятника от положения равновесия возникает вращательный момент:
где m – масса маятника; l – расстояние между точкой подвеса и центром инерции маятника.
Запишем для маятника уравнение динамики вращательного движения.
В случае малых колебаний
или
Слайд 14или
где
- период колебаний физического маятника
Из сопоставления формул получается, что математический маятник
будет иметь такой период колебаний, как и данный физический маятник.
- приведенная длина физического маятника.
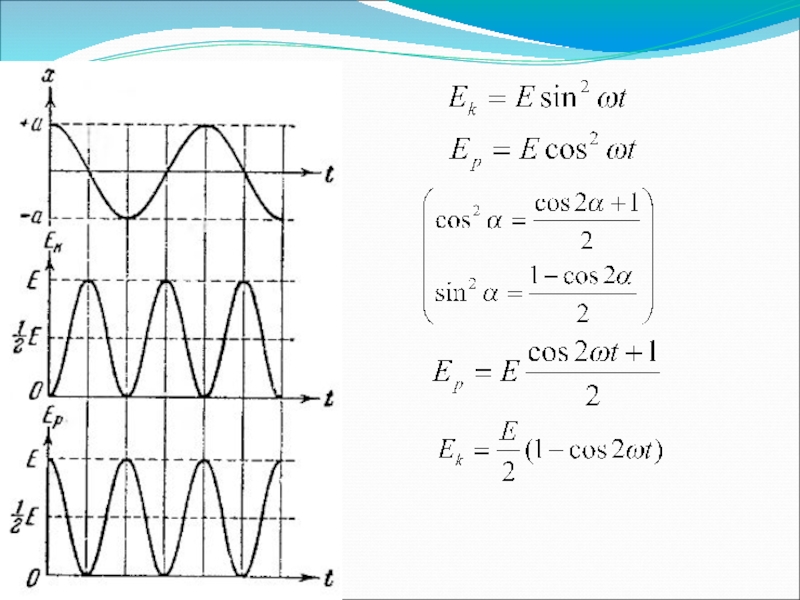
Слайд 154. Энергия гармонического колебания
Квазиупругая сила является консервативной. Поэтому полная энергия гармонического
Слайд 181. Затухающие колебания
Затухающими называются колебания, энергия которых уменьшается с течением времени.
Рассмотрим
Ограничимся рассмотрением малых колебаний.
r – коэффициент сопротивления
Напишем для колеблющегося тела 2-ой закон Ньютона:
или
где
Будем искать решение уравнения в виде:
где А(t) – некоторая функция времени.
(*)
Слайд 20I
II
I уравнение можно представить в виде:
Проинтегрируем и получим:
где
- постоянная интегрирования
Слайд 21Произведя потенцирование, получим
- зависимость амплитуды свободных затухающих колебаний от времени
подставим в
(разделим на А)
ω - частота затухающих колебаний
При условии, что
величина ω будет вещественной
Т.о. при небольшом затухании решение уравнения:
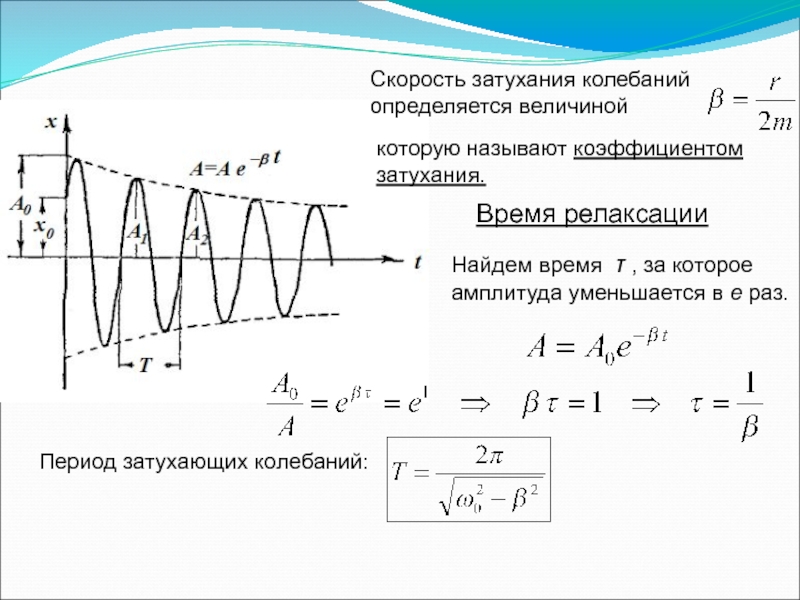
Слайд 22Скорость затухания колебаний определяется величиной
которую называют коэффициентом затухания.
Время релаксации
Найдем время τ
Период затухающих колебаний:
Слайд 23Отношение двух последующих амплитуд называют декрементом затухания:
D=1 – гармонические колебания;
D>1 –
D< 1 – колебания с возрастающей амплитудой;
D→∞ - апериодическое движение
Логарифм отношения двух последующих амплитуд называется логарифмическим декрементом затухания:
- добротность колебательной системы
Слайд 242. Вынужденные колебания
Вынужденными называются колебания, возникающие в колебательной системе под действием
Пусть вынуждающая сила изменяется со временем по гармоническому закону:
Предполагая колебания достаточно малыми, будем считать силу сопротивления пропорциональной скорости.
Тогда уравнение движения:
Неоднородное линейное дифференциальное уравнение второго порядка.
(*)
Слайд 25Общее решение однородного уравнения:
Найдем частное решение уравнения (*) в виде:
Подставим
в уравнение
Слайд 27Амплитуда вынужденных колебаний
Т.о. частное решение:
Общее решение кроме частного решения, содержит решение
Т.о., функция (1) описывает установившиеся вынужденные колебания.
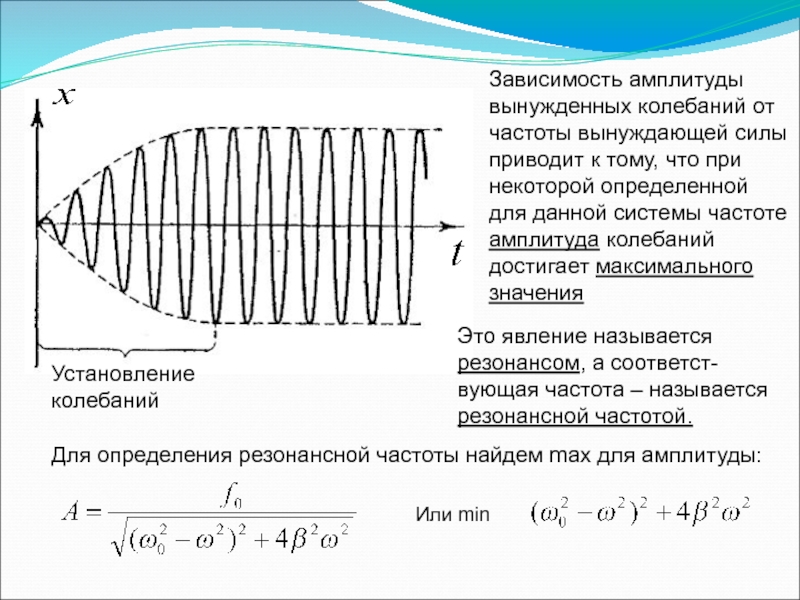
Слайд 28Установление колебаний
Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к
Это явление называется резонансом, а соответст-вующая частота – называется резонансной частотой.
Для определения резонансной частоты найдем max для амплитуды:
Или min
Слайд 29Продифференцировав подкоренное выражение по ω и приравняв нулю, получим условие ,
Это уравнение имеет три решения:
II и III
I
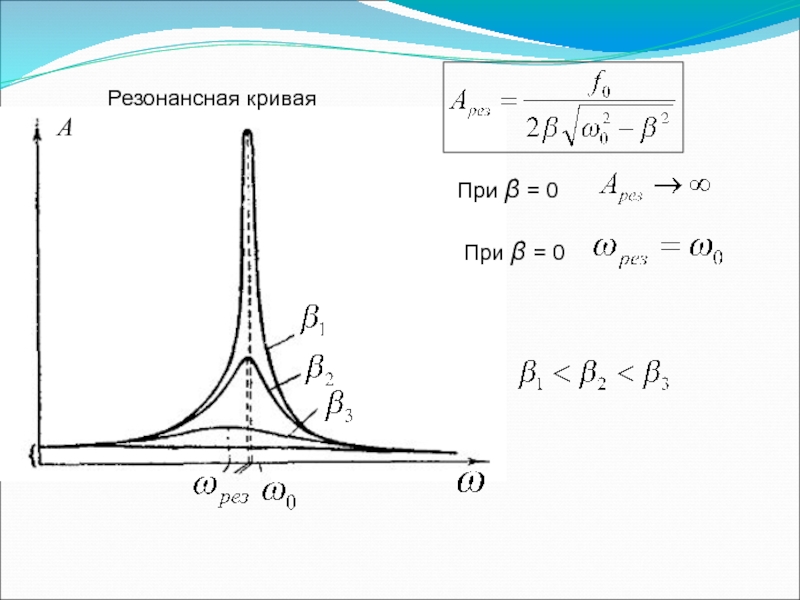
I решение (ω=0) соответствует максимуму знаменателя.
Для резонансной частоты получается одно значение:
Подставим в выражение для амплитуды и получим выражение для амплитуды при резонансе:
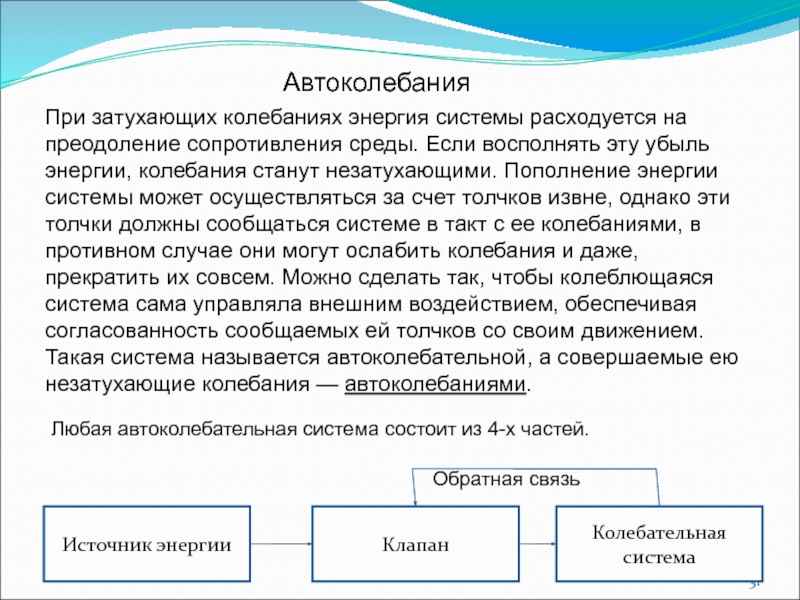
Слайд 31Автоколебания
При затухающих колебаниях энергия системы расходуется на преодоление сопротивления среды.
Обратная связь
Колебательная система
Клапан
Источник энергии
Любая автоколебательная система состоит из 4-х частей.
Слайд 321. Представление гармонических колебаний с помощью вращающегося вектора. 2. Сложение колебаний одинакового