- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Проблемы энергосбережения и ресурсосбережения в теплоэнергетике. Оребрение стенок презентация
Содержание
- 1. Проблемы энергосбережения и ресурсосбережения в теплоэнергетике. Оребрение стенок
- 2. Пути интенсификации теплопередачи Коэффициент теплопередачи для
- 3. Пути интенсификации теплопередачи Отсюда следует, что коэффициент
- 4. Пути интенсификации теплопередачи Коэффициент теплопередачи для цилиндрической
- 5. Пути интенсификации теплопередачи Из этих формул следует,
- 6. . . Интенсификация теплопередачи Если пренебречь
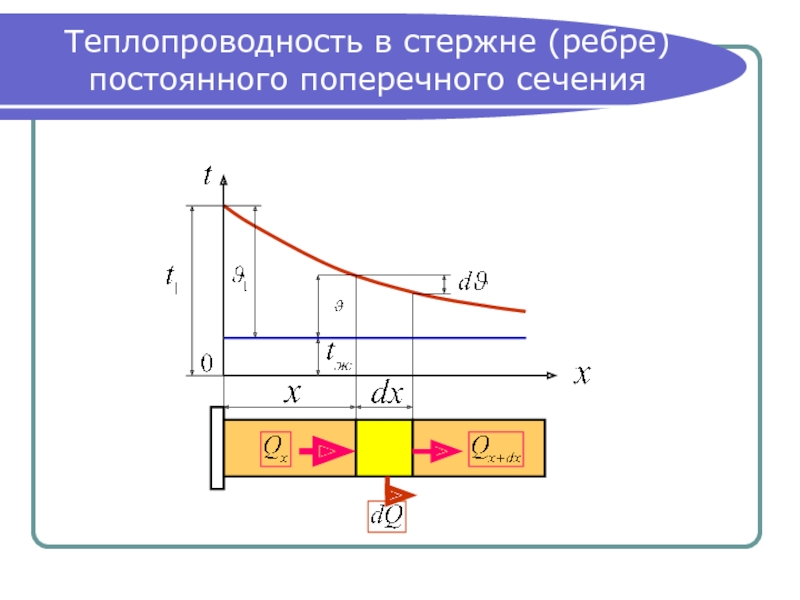
- 7. Теплопроводность в стержне (ребре) постоянного поперечного сечения
- 8. Условные обозначения Приняты следующие обозначения: ●
- 9. Уравнение теплового баланса При -
- 10. Конвективный тепловой поток По
- 11. Дифференциальное уравнение для избыточной температуры в
- 12. Стержень бесконечной длины Граничные условия: при
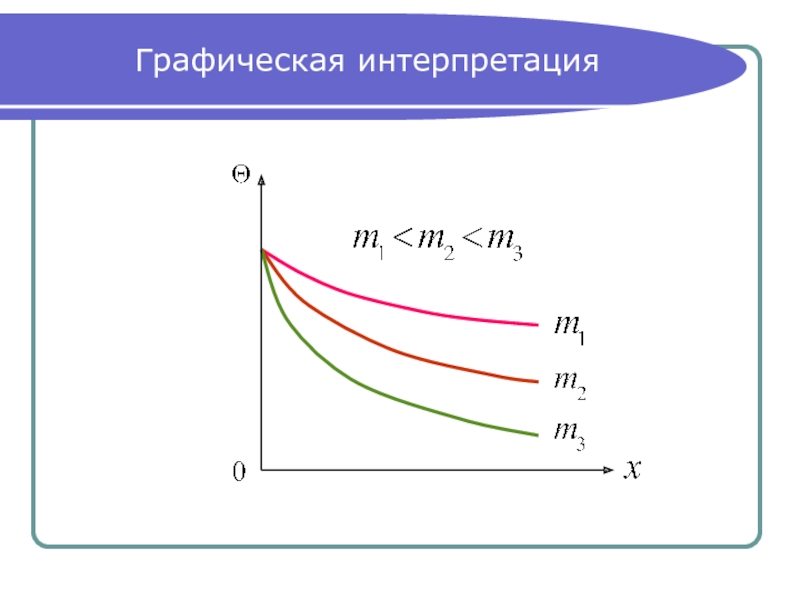
- 13. Графическая интерпретация
- 14. Теплота, отданная от стержня к жидкости
- 15. Теплота, отданная от стержня к жидкости
- 16. Б) Стержень конечной длины Граничные условия:
- 17. Стержень конечной длины Общее решение подчиним граничным условиям
- 18. Стержень конечной длины Решим систему.
- 19. Стержень конечной длины .
- 20. Стержень конечной длины Значения коэффициентов:
- 21. Стержень конечной длины Частное решение:
- 22. Стержень конечной длины Умножим и разделим на :
- 23. Стержень конечной длины Гиперболический синус и гиперболический косинус:
- 24. Стержень конечной длины Решение примет вид:
- 25. Стержень конечной длины Пусть теплоотдачей на конце стержня можно пренебречь:
- 26. Стержень конечной длины Температура на конце стержня при
- 27. Стержень конечной длины Тепловой поток через стержень: Здесь: Тогда:
- 28. Стержень конечной длины С учетом того, что: получим:
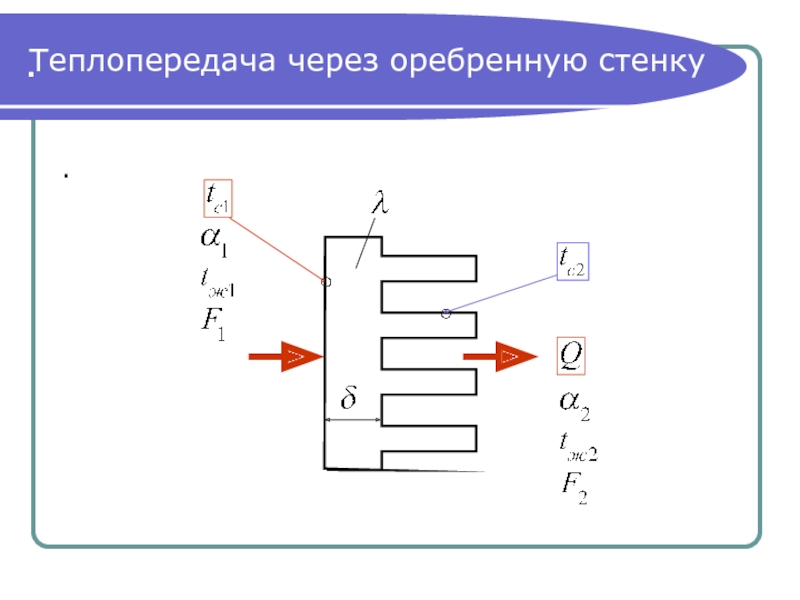
- 29. . . Теплопередача через оребренную стенку
- 30. . . Тепловой поток, переданный через
- 31. . . Эффект оребрения
- 32. Вопросы к экзамену Пути интенсификации теплопередачи. Дифференциальное
Пути интенсификации теплопередачи Коэффициент теплопередачи для плоской стенки:
Слайд 3Пути интенсификации теплопередачи
Отсюда следует, что коэффициент теплопередачи не может быть больше
самого малого коэффициента теплоотдачи.
Таким образом, целесообразно интенсифицировать теплообмен со стороны самого маленького коэффициента теплоотдачи.
Таким образом, целесообразно интенсифицировать теплообмен со стороны самого маленького коэффициента теплоотдачи.
Слайд 4Пути интенсификации теплопередачи
Коэффициент теплопередачи для цилиндрической стенки:
Коэффициент теплопередачи для шаровой
стенки:
Слайд 5Пути интенсификации теплопередачи
Из этих формул следует, что для цилиндрической и шаровой
стенки интенсивность теплообмена на поверхностях зависит не только от коэффициента теплоотдачи, но и от размера этих поверхностей.
Вывод: Таким образом, интенсивность теплообмена на поверхности тела можно изменить двумя способами:
Увеличить коэффициент теплоотдачи.
Увеличить площадь теплообмена.
Теплообмен интенсифицируют со стороны той поверхности, где термическое сопротивление наибольшее.
Вывод: Таким образом, интенсивность теплообмена на поверхности тела можно изменить двумя способами:
Увеличить коэффициент теплоотдачи.
Увеличить площадь теплообмена.
Теплообмен интенсифицируют со стороны той поверхности, где термическое сопротивление наибольшее.
Слайд 6.
.
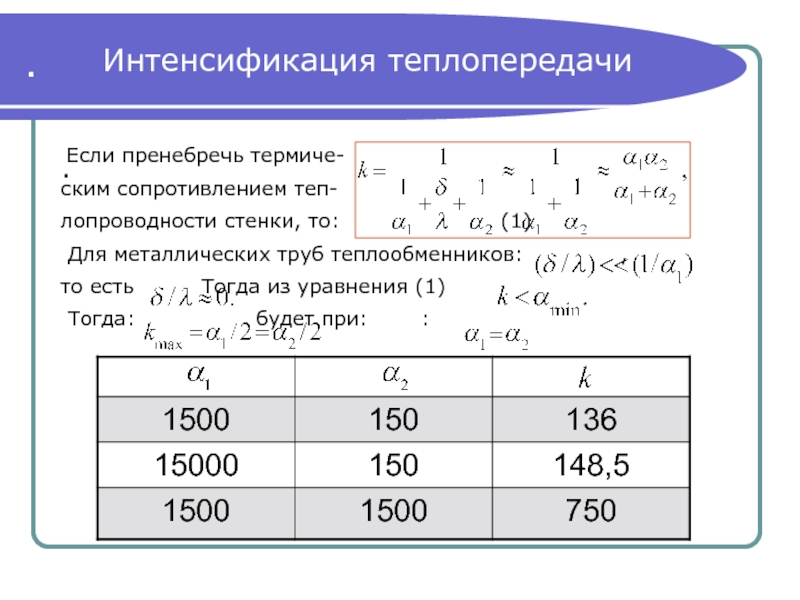
Интенсификация теплопередачи
Если пренебречь термиче-
ским сопротивлением теп-
лопроводности стенки, то: (1)
Для металлических труб теплообменников: ,
то есть Тогда из уравнения (1)
Тогда: будет при: :
то есть Тогда из уравнения (1)
Тогда: будет при: :
Слайд 8Условные обозначения
Приняты следующие обозначения:
● поперечное сечение стержня: , м²;
●
периметр стержня: , м;
● длина стержня: , м;
● коэффициент конвективной теплоотдачи:
, Вт/(м²К);
● температура окружающей среды: , °С;
● температура стержня: , °С;
● температура основания стержня: , °С;
● избыточная температура стержня: , К;
● избыточная температура основания стержня:
, К.
● длина стержня: , м;
● коэффициент конвективной теплоотдачи:
, Вт/(м²К);
● температура окружающей среды: , °С;
● температура стержня: , °С;
● температура основания стержня: , °С;
● избыточная температура стержня: , К;
● избыточная температура основания стержня:
, К.
Слайд 9Уравнение теплового баланса
При - бесконечный стержень
(температура изменяется только вдоль
оси х).
Уравнение теплового баланса, Вт: , (1)
где - теплота, отдаваемая от наружной поверхности
стержня к окружающей жидкости за счет конвекции;
- теплота, подведенная теплопроводностью к левой
стороне элемента dx;
- теплота, отведенная теплопроводностью
от правой стороны элемента dx.
Уравнение теплового баланса, Вт: , (1)
где - теплота, отдаваемая от наружной поверхности
стержня к окружающей жидкости за счет конвекции;
- теплота, подведенная теплопроводностью к левой
стороне элемента dx;
- теплота, отведенная теплопроводностью
от правой стороны элемента dx.
Слайд 10Конвективный тепловой поток
По закону Фурье для теплопроводности:
После подстановки
их в (1) имеем: (2)
Конвективный тепловой поток по
уравнению Ньютона-Рихмана: (3)
где udx = dF – боковая поверхность, м².
Слайд 11Дифференциальное уравнение
для избыточной температуры в стержне
Подставляем (2) и (3)
в (1):
После сокращения на dx получаем дифференциальное
уравнение для избыточной температуры в стержне:
(4) где
Для , тогда при постоянном
сечении ребра интеграл от выражения (4): (5)
Константы интегрирования для конкретных случаев
определяются из граничных условий.
Слайд 12Стержень бесконечной длины
Граничные условия: при (6)
так как при вся теплота будет отдана жидкости.
Подставляем (6) в (5): при (7)
(8)
Из (8): так как , то с1 = 0 . (9)
Из (7): то есть с2 = . (10)
После подстановки констант интегрирования в (5) имеем:
(11) или безразмерный
избыток температуры: (12)
Слайд 14Теплота, отданная от стержня
к жидкости
По предыдущему слайду при
все кривые
асимптотически приближаются к оси абсцисс.
Из выражения:
следует, что m пропорциональна теплоотдаче с боковой
поверхности и обратно пропорциональна тепло-
проводности вдоль стержня , то есть надо выбирать
материал для ребер с высокой теплопроводностью.
Теплота, отданная от стержня к жидкости, равна теплоте,
прошедшей через его основание, Вт: (13)
асимптотически приближаются к оси абсцисс.
Из выражения:
следует, что m пропорциональна теплоотдаче с боковой
поверхности и обратно пропорциональна тепло-
проводности вдоль стержня , то есть надо выбирать
материал для ребер с высокой теплопроводностью.
Теплота, отданная от стержня к жидкости, равна теплоте,
прошедшей через его основание, Вт: (13)
Слайд 16Б) Стержень конечной длины
Граничные условия:
- коэффициент
теплоотдачи на конце стержня;
- избыточная температура на конце стержня.
- избыточная температура на конце стержня.
Слайд 30.
.
Тепловой поток, переданный
через оребренную стенку
При стационарном тепловом режиме тепловой
поток
со стороны горячей и холодной жидкости, а также внутри
стенки один и тот же:
(2)
Разрешим (2) относительно падений температур,
сложим их между собой и найдем тепловой поток:
со стороны горячей и холодной жидкости, а также внутри
стенки один и тот же:
(2)
Разрешим (2) относительно падений температур,
сложим их между собой и найдем тепловой поток:
Слайд 31.
.
Эффект оребрения
или
где коэффициент теплопередачи,
Вт/(м²К):
приведенный коэффициент теплоотдачи
При коэффициенте оребрения :
тогда коэффициент теплопередачи k = 750 Вт/(м²К).
приведенный коэффициент теплоотдачи
При коэффициенте оребрения :
тогда коэффициент теплопередачи k = 750 Вт/(м²К).
Слайд 32Вопросы к экзамену
Пути интенсификации теплопередачи. Дифференциальное уравнение теплопроводности в ребре постоянного
поперечного сечения.
Теплопроводность в стержне бесконечной длины.
Теплопроводность в стержне конечной длины. Передача теплоты через ребристую плоскую стенку.
Теплопроводность в стержне бесконечной длины.
Теплопроводность в стержне конечной длины. Передача теплоты через ребристую плоскую стенку.
