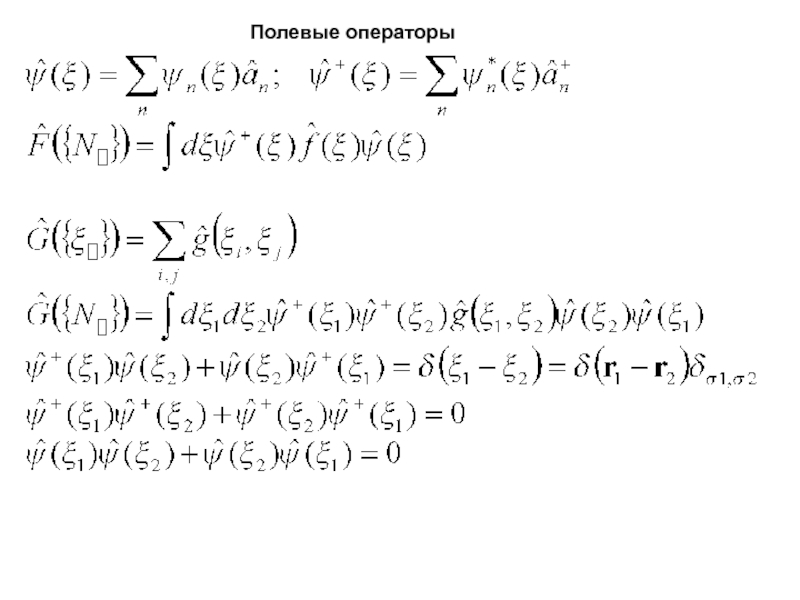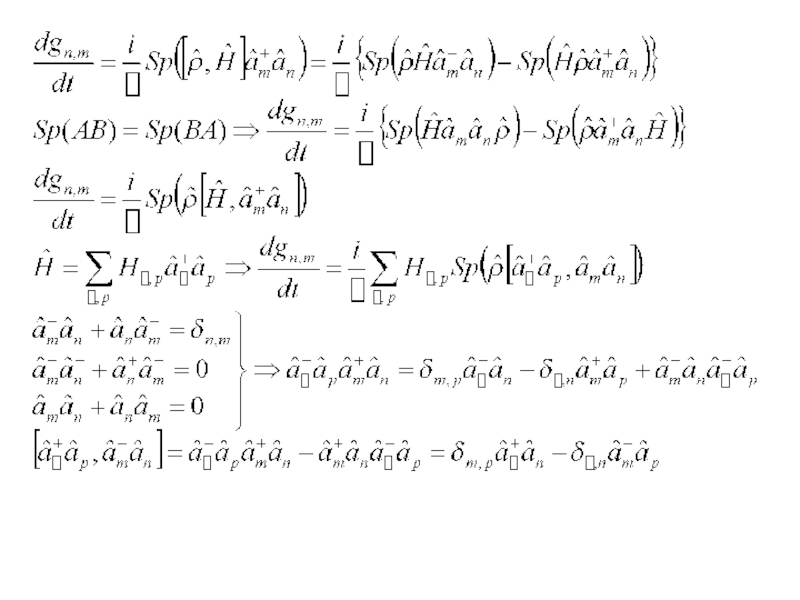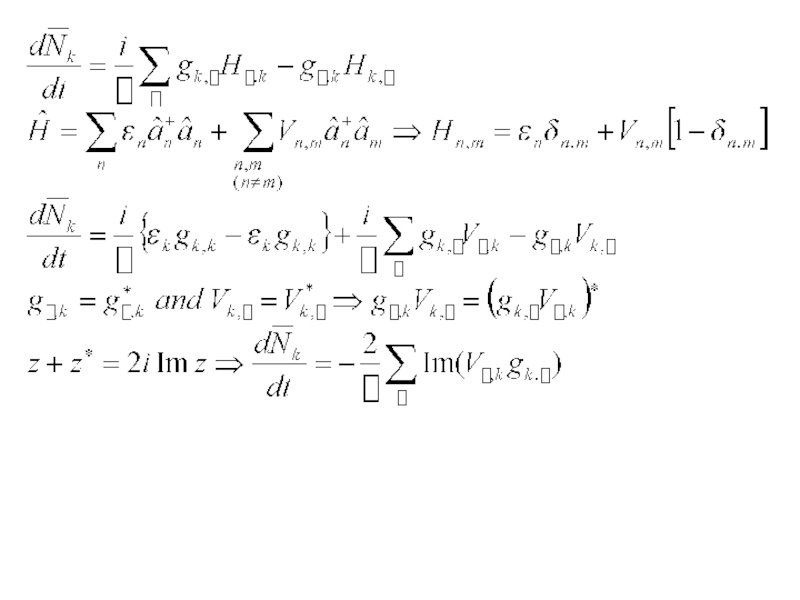- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Представление вторичного квантования (фермионы) презентация
Содержание
- 1. Представление вторичного квантования (фермионы)
- 2. Есть система тождественных фермионов - Гамильтониан системы
- 3. Стационарные состояния системы невзаимодействующих тождественных фермионов
- 4. - Принцип запрета Паули
- 5. Волновую функцию произвольного состояния системы тождественных фермионов
- 6. - Оператор числа частиц в одночастичном состоянии m Антикоммутационные соотношения – следствие принципа запрета Паули
- 7. Полевые операторы
- 8. Одноэлектронная матрица плотности
- 9. Если система взаимодействует с окружающей средой, то
- 10. Можно диаганолизовать (построить базис из собственных векторов)
- 11. Классическая теория. Термодиномическое состояние описывается функцией распределения
- 12. - Классическое уравнение Лиувилля - Скобка Пуассона
- 13. Квантовая теория. Термодинамические свойства системы описываются оператором
- 14. - Классическое уравнение Лиувилля Гамильтониан и оператор
- 15. Вычисление производных величин по времени
- 16. Система тождественных фермионов Вычисляем шпур по
- 17. Совпадает с матр. Элем. Опер. - Вычисляется
- 18. Уравнение для одночастичной матрицы плотности (одночастичное уравнение
- 20. - Одночастичное уравнение Лиувилля
- 21. - Поток частиц в энергетическом пр-ве из сост. k
Слайд 2Есть система тождественных фермионов
- Гамильтониан системы невзаимодействующих фермионов
- Гамильтониан одного электрона
- Гамильтониан взаимодействия между фермионами
Представление вторичного квантования – представление по базису из волновых функций стационарных состояний невзаимодействующей системы
Слайд 3Стационарные состояния системы невзаимодействующих тождественных фермионов
1) Находим одночастичные стационарные состояния (уровни
2) В стационарном состоянии всей системы в целом каждая из частиц находится в одном из одночастичных стационарных состояний. Поэтому стационарное состояние всего газа в целом однозначным образом задается указанием чисел заполнения всех одночастичных стационарных состояний .
3) Для ферми-газа справедлив принцип запрета Паули, согласно которому в одном одночастичном стационарном состоянии не может находится более одного фермиона. Поэтому число заполнения одночастичного стационарного состояния может принимать только два значения или 0, или 1.
Слайд 5Волновую функцию произвольного состояния системы тождественных фермионов (в том числе и
- Волновая функция в представлении по базису из стационарных состояний невзаимодействующей системы (в представлении вторичного квантования)
- оператор F в представлении вторичного квантования
Слайд 6- Оператор числа частиц в одночастичном состоянии m
Антикоммутационные соотношения – следствие
Слайд 9Если система взаимодействует с окружающей средой, то ее нельзя описать собственной
Используется более общий аппарат квантовой механики – теория матрицы плотности
Постулат фон Неймана. Можно ввести эрмитовый оператор ρ (оператор плотности), который действует только на координаты изучаемой макроскопической системы и содержит в себе всю информацию об окружающей среде, существенную для описания макроскопического состояния изучаемой системы. Статистическое среднее физической величины системы
- Шпур не зависит от порядка следования операторов
Шпур не зависит от выбора базиса => статистическое среднее можно вычислять по любому базисному набору волновых функций изучаемой системы (выбор базиса – вопрос удобства)
Вычисляется по базису из волновых функций нашей
системы (в пренебрежении ее взаимодействия с окружающей средой)
Слайд 10Можно диаганолизовать (построить базис из собственных векторов)
-формальное определение вероятности
- Можно интерпретировать
Слайд 11Классическая теория. Термодиномическое состояние описывается функцией распределения ρ(q,p,t).
Ключевой момент -
Слайд 12- Классическое уравнение Лиувилля
- Скобка Пуассона
В равновесии функция распределения явно зависит
- Каноническое распределение (фикс. Число частиц)
- стат. интеграл
- Термодинамический потенциал (свободная энергия Гельмгольца)
- Большое каноническое распределение (переменное число частиц)
- большой статистический интеграл
- большой термодинамический потенциал
Слайд 13Квантовая теория. Термодинамические свойства системы описываются оператором плотности.
- «Квантовомеханический оператор
Вследствие того, что энергия взаимодействия системы с окружающей средой существенно меньше ее внутренней энергии, то систему можно полагать квазизамкнутой и считать
- Квантовое уравнение Лиувилля
Слайд 14- Классическое уравнение Лиувилля
Гамильтониан и оператор плотности имеют общий базис
- Каноническое
- стат. сумма
- Термодинамический потенциал (свободная энергия Гельмгольца)
- Большое каноническое распределение (переменное число частиц)
- большой статистический интеграл
- большой термодинамический потенциал
В оператор плотности явно зависит только от оператора Гамильтона
Слайд 16Система тождественных фермионов
Вычисляем шпур по базису из Слеттеровских определителей
- Одночастичный
- формируют базис для системы частиц
Слайд 17Совпадает с матр. Элем. Опер.
- Вычисляется по одночастичному базису
- Эрмитова матрица
-
Слайд 18Уравнение для одночастичной матрицы плотности (одночастичное уравнение Лиувилля) для системы невзаимодействующих
Рассмотрим систему тождественных невзаимодействующих фермионов ( или с взаимодействием, учтеным в приближении самосогласованного поля Хартри).
- одночастичный базис