- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Атом Бора презентация
Содержание
- 1. Атом Бора
- 2. «Лирическое отступление» – «атом» у древних греков
- 3. «Лирическое отступление» – атом Бошковича Руджер Иосип
- 4. «Лирическое отступление» – атом Томсона Джозеф-Джон Томсон
- 5. Эрнест Резерфорд (1871 - 1937). Лауреат Нобелевской
- 6. Схема опыта Резерфорда по рассеянию α-частиц.
- 7. Трудности модели – согласно классической электродинамике ускоренный
- 8. Планетарная модель атома и принципы квантования
- 9. Формализм: Равенство сил для круговой
- 10. Планетарная модель атома и принципы квантования Вспоминая
- 11. «Волны материи»
- 12. В 1924 г. де Бройль представил свою
- 13. Идея де Бройля (по аналогии со струной):
- 14. Гипотеза де Бройля. В статье "Интерпретация квантовой
- 15. Волновые свойства частиц. Дэвиссон и Джермер открыли
- 16. Опыт Дэвиссона-Джермера Схема опыта Дэвиссона и Джермера.
- 17. Немного цитат ☺ «Если это правильно, то
- 18. Немного цитат ☺ «Законы квантования в своей
- 19. Принципы неопределенности и дополнительности
- 20. Принцип неопределенности Оценка длины волны λ,
- 21. Принцип неопределенности В общем виде принцип
- 22. Чтобы выразить смысл и значение принципа неопределенности
- 23. С точки зрения экспериментатора, принцип дополнительности означает,
- 24. Опыты по измерению физических величин. Измерение
- 25. Измерение импульса. Пусть частица - это
- 26. Таким образом, момент испускания фотона определяется только
- 27. Дифракционный опыт. Пусть R>>a>>λ, тогда распределение интенсивности
- 28. Чтобы дифракционная картинка сохранилась, неопределенность Δpy должна
- 29. Дифракция электронов при прохождении сквозь фольгу. Распределение
- 30. Схема опыта по дифракции электронов. K
- 31. Дифракция электронов на щели. График справа –
- 32. Волновая функция
- 33. Волновая функция. Соотношение между импульсом и
- 34. «Волна – частица»
- 35. Волновые пакеты в пространстве и времени.
- 36. Ряд и интеграл Фурье Периодическая функция
- 37. Можно показать, что
- 38. Аналогично можно исследовать зависимость ψ от
Слайд 2«Лирическое отступление» – «атом» у древних греков
«… остаётся признать неизбежно
Тит Лукреций Кар
«О природе вещей»
Слайд 3«Лирическое отступление» – атом Бошковича
Руджер Иосип Бошкович (18 мая 1711, Рагуз
Создал оригинальную атомиcтическую теорию (атом как центр силы).
Из книги Бошковича “Теория натуральной философии, сведенная к единому закону сил, существующих в природе”, изданной в Вене в 1758 г.:
“Я не допускаю совершенно непрерывную протяженность материи, но составляю ее из точек, совершенно неделимых и непротяженных, отделенных друг от друга неким интервалом и связанных некими силами, то притягательными, то отталкивательными, зависящими от расстояния между этими точками”.
“Требуется, чтобы природа избегала во всем и во всех случаях скачков с помощью такой силы, которая при уменьшении расстояния возрастала бы до бесконечности, и притом так возрастала, чтобы она была способна обратить в ноль любую скорость, сколь угодно большую. Следовательно, мы приходим к силам отталкивания, возрастающим до бесконечности при уменьшении расстояния”.
Согласно гипотезе Бошковича, по мере увеличения расстояния между точками сила отталкивания, доминирующая при сверхмалых расстояниях, плавно переходит в силу притяжения, затем опять в силу отталкивания и так несколько раз.
Слайд 4«Лирическое отступление» – атом Томсона
Джозеф-Джон Томсон (1856-1940) - английский физик, Нобелевская
Атом Томсона
Слайд 5Эрнест Резерфорд (1871 - 1937).
Лауреат Нобелевской премии по химии 1908г.
«За проведенные
Открыл альфа- и бета-излучение.
Открыл и объяснил радиоактивное превращение химических элементов, создал теорию радиоактивного распада.
Предложил и экспериментально обосновал планетарную модель атома.
Планетарная модель атома - Эрнест Резерфорд
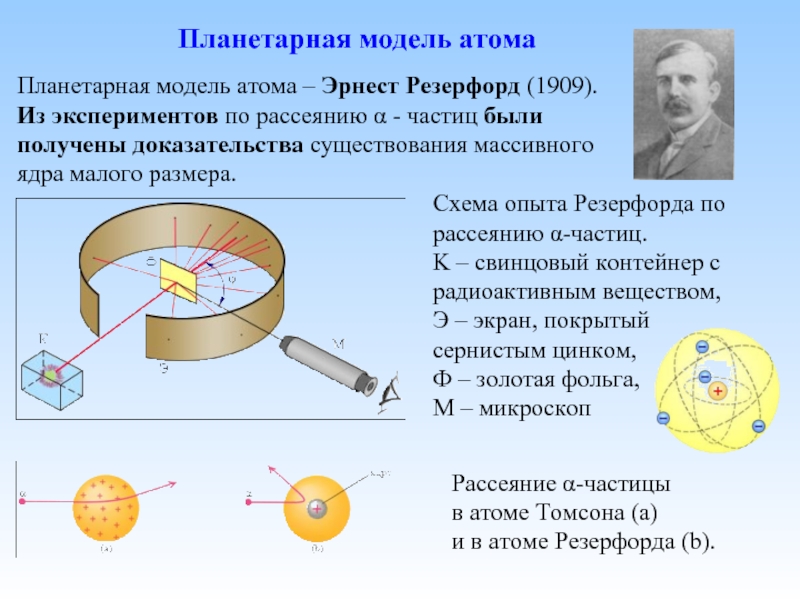
Слайд 6Схема опыта Резерфорда по рассеянию α-частиц. K – свинцовый контейнер с
Планетарная модель атома – Эрнест Резерфорд (1909).
Из экспериментов по рассеянию α - частиц были получены доказательства существования массивного ядра малого размера.
Планетарная модель атома
Рассеяние α-частицы
в атоме Томсона (a)
и в атоме Резерфорда (b).
Слайд 7Трудности модели – согласно классической электродинамике ускоренный электрон излучает э.-м. волны.
Для устранения противоречия и объяснения атомных спектров Н. Бор в 1913 г. сформулировал 2 постулата:
1) О стационарных состояниях: В атоме существуют орбиты, вращаясь по которым, электрон не излучает
2) О квантовых скачках: Излучение происходит только при перескоке электрона с одной стационарной орбиты на другую
Планетарная модель атома и принципы квантования
Слайд 8
Планетарная модель атома и принципы квантования
Нильс Хенрик Давид Бор (7 октября
Создатель первой квантовой теории атома и активный участник разработки основ квантовой механики.
Сформулировал количественно так называемый принцип соответствия, связывающий квантовую теорию с классической физикой.
В рамках физической интерпретации квантовой механики сформулировал принцип дополнительности.
Слайд 9 Формализм:
Равенство сил для круговой орбиты
(идеализированный атом водорода):
При этом
Кроме того, круговое движение характеризуется еще моментом количества движения (орбитальный момент) l:
Согласно Бору, величина l не произвольна, а кратна ћ = h / 2π :
Планетарная модель атома и принципы квантования
Из (1) и (2) можно получить выражения для разрешенных значений:
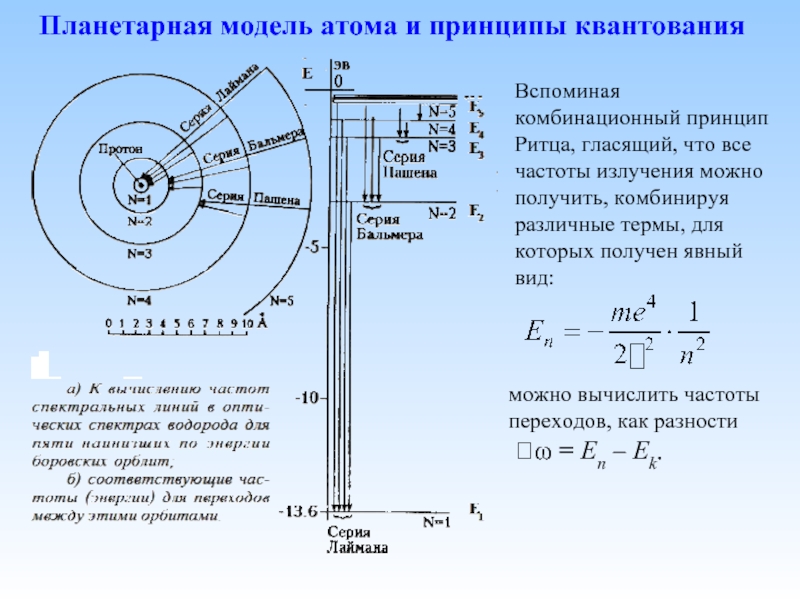
Слайд 10Планетарная модель атома и принципы квантования
Вспоминая комбинационный принцип Ритца, гласящий, что
можно вычислить частоты переходов, как разности
ω = En – Ek.
Слайд 12В 1924 г. де Бройль представил свою работу "Исследования по квантовой
1892—1987
Луи де БРОЙЛЬ
(Broglie)
Закончил факультет искусств и литературы Парижского университета, где в 1910 г. получил степень бакалавра. Затем увлекся физикой и в 1913 г. получил ученую степень по физике на факультете естественных наук Парижского университета.
В том же году был призван на военную службу и зачислен во французский инженерный корпус. После начала в 1914г. первой мировой войны он служил в радиотелеграфном дивизионе и провел большую часть военных лет на станции беспроволочного телеграфа при Эйфелевой башне. Через год после окончания войны он возобновил свои занятия физикой в частной лаборатории своего брата. Изучал поведение электронов, атомов и рентгеновских лучей.
Слайд 13Идея де Бройля (по аналогии со струной): Движение электрона по орбите будет
Гипотеза де Бройля.
Де Бройль пытался понять физический смысл постулатов Бора.
Точнее, смысл квантования орбитального момента:
Вопрос де Бройля:
Если свет ведет себя то как волна, то как частица (фотон), то не является ли такой дуализм свойством не только фотона, но и других частиц?
Фотон, как частица, характеризуется энергией E и импульсом p.
Импульс фотона простым образом связан с волновым вектором k электромагнитной волны:
Вместе с постулатом Бора это дает:
Слайд 14Гипотеза де Бройля.
В статье "Интерпретация квантовой механики" Луи де Бройль писал:
"Я
…Я смог установить следующие основные формулы между энергией E и количеством движения p свободно движущейся корпускулы, с одной стороны, частотой ν и длиной волны λ ассоциированной плоской монохроматической волны, с другой стороны.
где h - постоянная Планка. Эти формулы, будучи применёнными к фотону, содержали, как частный случай, формулы световых квант (то, что мы сейчас называем фотонами)"
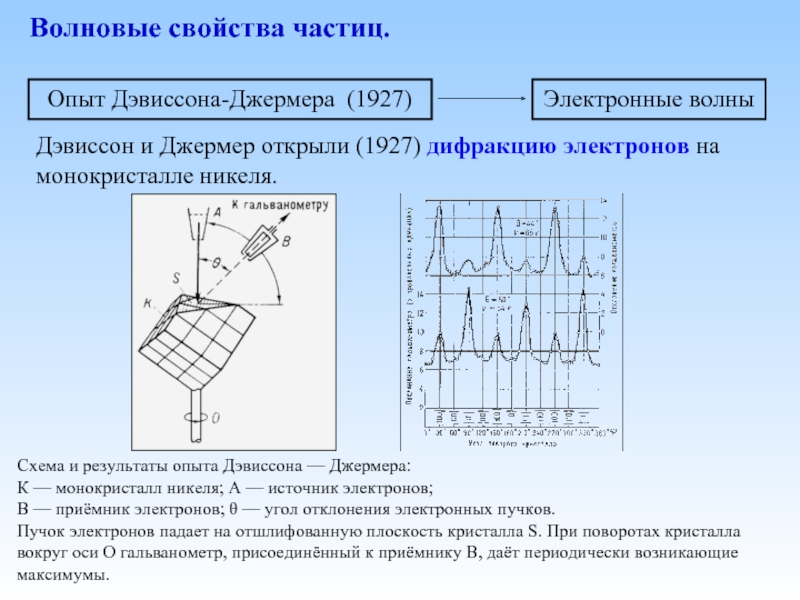
Слайд 15Волновые свойства частиц.
Дэвиссон и Джермер открыли (1927) дифракцию электронов на монокристалле
Схема и результаты опыта Дэвиссона — Джермера:
К — монокристалл никеля; А — источник электронов;
В — приёмник электронов; θ — угол отклонения электронных пучков.
Пучок электронов падает на отшлифованную плоскость кристалла S. При поворотах кристалла вокруг оси О гальванометр, присоединённый к приёмнику В, даёт периодически возникающие максимумы.
Электронные волны
Опыт Дэвиссона-Джермера (1927)
Слайд 16Опыт Дэвиссона-Джермера
Схема опыта Дэвиссона и Джермера.
П — электронная пушка, К
Отраженный луч наблюдается только в том случае, если длина волны соответствует условию Брэгга:
где ϕ— угол скольжения, d — постоянная решетки, n — порядок интерференции.
Слайд 17Немного цитат ☺
«Если это правильно, то это означает конец физики как
«Я убежден, что это учение является роковым для здорового развития науки» (А. Шустер, 1913 г.).
«Атом существует вечно, мы это бесспорно знаем. Но понимаем ли мы это? Нет, не понимаем. Наше непонимание мы прикрываем непонятными же квантовыми условиями. Процесс лучеиспускания — это акт возрождения разрушенного атома. Механизм его нам непонятен. Свое непонимание мы вновь прикрываем непонятным квантовым условием, второй гипотезой Бора... Весь этот метод Бора основан на квантовании — совершенно слепом, мало логическом процессе мысли, на формальной, если можно так выразиться, интуиции» (Д. С. Рождественский, 1919 г.).
«Теория квантов подобна другим победам в науке: месяцами вы улыбаетесь им, а затем годами плачете» (Г. Крамерс, 1920 г.).
Слайд 18Немного цитат ☺
«Законы квантования в своей теперешней формулировке носят до некоторой
«Мы неизмеримо далеки от такого описания атомного механизма, которое позволило бы проследить, например, все движения электрона в атоме или понять роль стационарных состояний... Теорию квантов можно сравнить с лекарством, излечивающим болезнь, но убивающим больного». (Г. Крамерс, X. Гольст, 1923 г.)
«Все это очень красиво и крайне важно, но, к сожалению, не очень понятно. Мы не понимаем ни гипотезы Планка об осцилляторах, ни запрета нестационарных орбит, и мы не понимаем, как же, в конце концов, образуется свет согласно теории Бора. Не подлежит сомнению, что механику квантов, механику дискретного, еще предстоит создать» (Г.А. Лоренц, 1923 г.).
«Физика теперь снова зашла в тупик, во всяком случае для меня она слишком трудна, и я предпочел бы быть комиком в кино или кем-нибудь вроде этого и не слышать ничего о физике!» (В. Паули, 21 мая 1925 г.).
Слайд 20Принцип неопределенности
Оценка длины волны λ, полученная де Бройлем для электронов,
Сравним количественные значения длины волны λ с размерами 1-ой стационарной орбиты атома водорода, вычисленного по теории Бора.
Подстановка в (*) скорости электрона на 1-ой орбите
дает значение
Вспоминая, что радиус этой орбиты
немедленно получаем отношение
Это означает, что на размерах орбиты укладывается 1/6 периода! Тем самым теряется смысл разговоров о «траектории» электрона в атоме.
Дело в том, что для оценки длины волны, мы должны достаточно ТОЧНО знать значение скорости электрона. Оказывается, этого достаточно, чтобы НЕТОЧНОСТЬ в определении его положения превысила размеры системы, в которой он находится.
Слайд 21Принцип неопределенности
В общем виде принцип неопределенности был сформулирован Гейзенбергом в
Примерами таких пар являются:
координата частицы x и соответствующая компонента импульса px ;
z-компонента Jz момента импульса и угол поворота ϕ в плоскости xy;
энергия частицы E и момент времени t ее измерения.
В количественной формулировке принцип неопределенности утверждает, что произведение неопределенностей двух сопряженных переменных по порядку величины не меньше постоянной Планка
Другими словами, невозможно точно определить значение одной из величин пары, не потеряв при этом всех сведений о второй величине.
Слайд 22Чтобы выразить смысл и значение принципа неопределенности в более «физических» терминах,
Согласно этому принципу, атомные явления невозможно описывать с той полнотой, какая требуется классической динамикой. Ряд величин, дополняющих друг друга и дающих полное классическое описание, фактически являются «взаимоисключающими».
Формулировки принципа дополнительности:
Ни в каком эксперименте невозможно одновременно наблюдать корпускулярные и волновые свойства микрочастиц.
В дальнейшем была предложена более общая формулировка, содержащая предыдущую как частный случай: получение экспериментальной информации об одних физических величинах, описывающих микрообъект, неизбежно связано с потерей информации о некоторых других величинах.
Принцип дополнительности.
Слайд 23С точки зрения экспериментатора, принцип дополнительности означает, что, в силу свойств
Если исходить из принципа дополнительности, то корпускулярно-волновой дуализм квантовых объектов перестает быть парадоксальным: волновой и корпускулярный аспекты оказываются дополнительными и проявляются во взаимоисключающих экспериментальных условиях. Всякая попытка выявить один из аспектов, требует соответствующего экспериментального устройства, которое лишает нас возможности наблюдать другой аспект поведения объекта.
Принцип дополнительности.
Слайд 24Опыты по измерению физических величин.
Измерение координаты.
Измерение координаты частицы P
Максимальная разрешающая способность линзы
Импульс фотона после рассеяния
Неопределенность x-компоненты импульса фотона
Согласно закону сохранения импульса неопределенность импульса частицы после рассеяния равна неопределенности импульса фотона
Отсюда немедленно следует
Слайд 25Измерение импульса.
Пусть частица - это атом в возбужденном состоянии. Когда
так что
Достаточно точное измерение импульса mv путем измерения частоты ω требует относительно большого времени τ. Минимальная ошибка
Слайд 26Таким образом, момент испускания фотона определяется только с точностью до τ.
Неопределенность импульса составляет
а произведение Δx∙Δp :
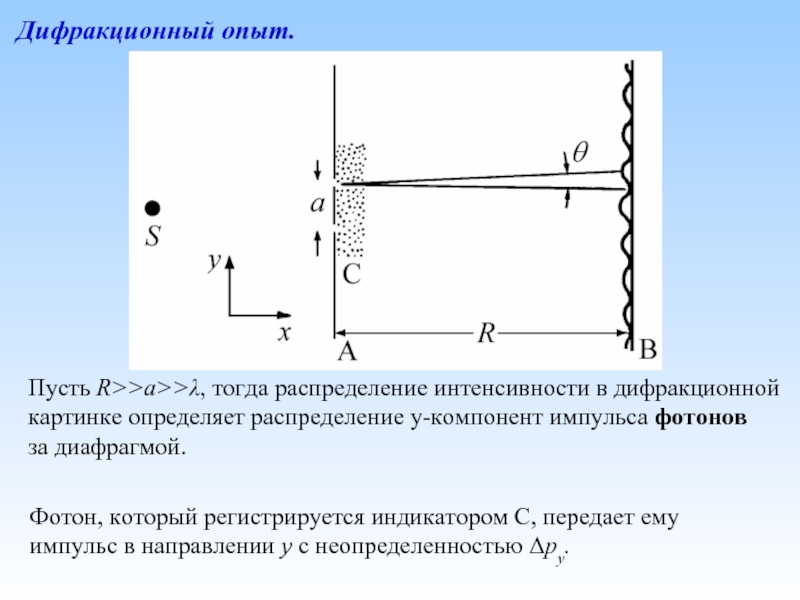
Слайд 27Дифракционный опыт.
Пусть R>>a>>λ, тогда распределение интенсивности в дифракционной
картинке определяет распределение
за диафрагмой.
Фотон, который регистрируется индикатором С, передает ему импульс в направлении y с неопределенностью Δpy.
Слайд 28Чтобы дифракционная картинка сохранилась, неопределенность Δpy должна быть много меньше импульса,
Из теории дифракции известно, что
Чтобы знать через какую щель прошел фотон, неопределенность y-координаты индикатора должна быть
Таким образом
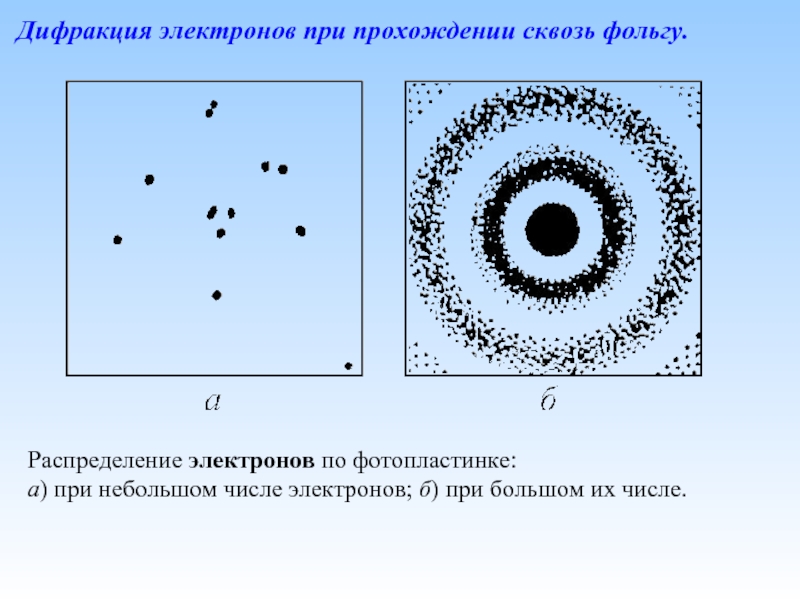
Слайд 29Дифракция электронов при прохождении сквозь фольгу.
Распределение электронов по фотопластинке:
а) при небольшом
Слайд 30Схема опыта по дифракции электронов. K – накаливаемый катод, A –
Дифракция электронов на поликристаллическом образце при длительной (a) и короткой (b) экспозиции. В случае (b) видны точки попадания отдельных электронов на фотопластинку.
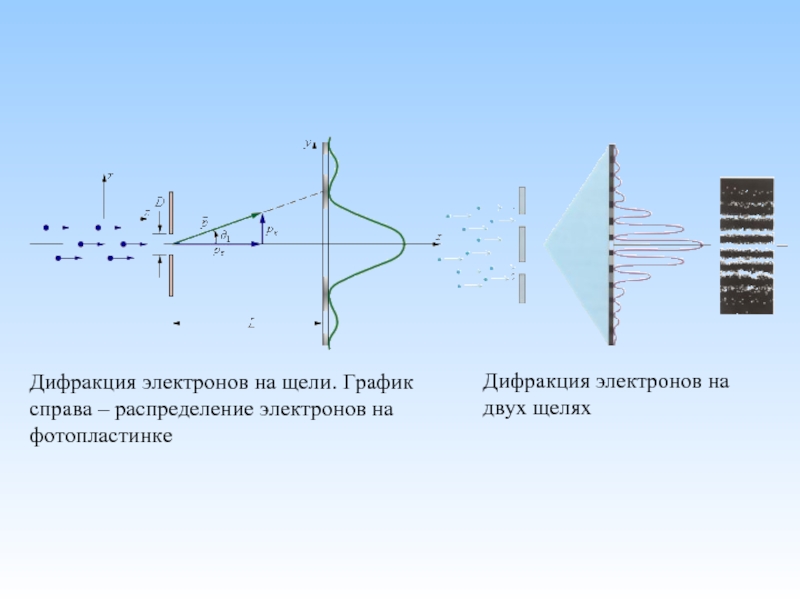
Слайд 31Дифракция электронов на щели. График справа – распределение электронов на фотопластинке
Дифракция электронов на двух щелях
Слайд 33Волновая функция.
Соотношение между импульсом и длиной волны:
Это справедливо и для
То, что квантовые частицы проявляют волновые свойства, наводит на мысль использовать для их описания волновую функцию ψ, зависящую от пространственных координат и времени и обладающую следующими свойствами:
Функция ψ может интерферировать сама с собой;
Абсолютное значение ψ велико там, где наиболее вероятно нахождение частицы или фотона;
Функция ψ описывает поведение отдельной частицы или фотона, а не статистическое распределение многих частиц.
Соотношение между энергией кванта и частотой колебаний:
Слайд 35Волновые пакеты в пространстве и времени.
Волновые образования в ограниченной области
λ0 - средняя длина волны, Δx – приблизительный размер пакета
Слайд 36Ряд и интеграл Фурье
Периодическая функция может быть представлена в виде
Другая форма записи этого ряда:
Для представления апериодических функций используется интеграл Фурье:
Слайд 38
Аналогично можно исследовать зависимость ψ от времени
Соотношение между интервалом времени и
Используя
, получаем
Замечание:
Из-за дисперсии скорости волновые пакеты, вообще говоря, расплываются со временем. Поэтому, строго говоря, нельзя отождествлять частицу с некой локализованной в пространстве совокупностью волн.