- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Переменный ток. Метод симметричных составляющих презентация
Содержание
- 1. Переменный ток. Метод симметричных составляющих
- 2. 2003г. Метод симметричных составляющих 1.Разложение несимметричной системы
- 3. 2003г. EA EB EC = + +
- 4. 2003г. Перепишем симметричные составляющие с учетом вращающего множителя
- 5. 2003г. 1) 2) 3) Сложим уравнения 1,2,3
- 6. 2003г. 4. 5. 6. 1. Сложим
- 7. 2003г. 2. 7. 8. 9. Сложим уравнения 7,8,9 системы 2.
- 8. 2003г. = 0 =
- 9. 2003г. А Сопротивления фаз динамической нагрузки для
- 10. 2003г. Метод симметричных составляющих 1.Разложение несимметричной системы
- 11. 2003г. На двигатель подается система напряжений прямой
- 12. 2003г. Как и в любой симметричной трехфазной
- 13. 2003г. Для того чтобы ротор двигателя вращался
- 14. 2003г. Во всех силовых электротехнических устройствах (трехфазных электродвигателях, генераторах и т.д.) Z2
- 15. 2003г. Сопротивления фаз для токов нулевой последовательности
- 16. 2003г. Режим нулевой последовательности отличается от
- 17. 2003г. b) Без нулевого провода При
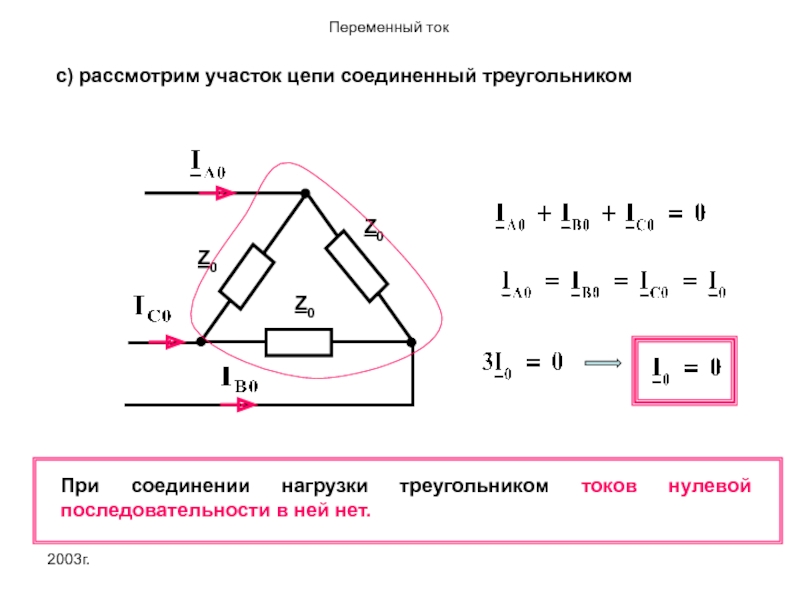
- 18. 2003г. с) рассмотрим участок цепи соединенный треугольником
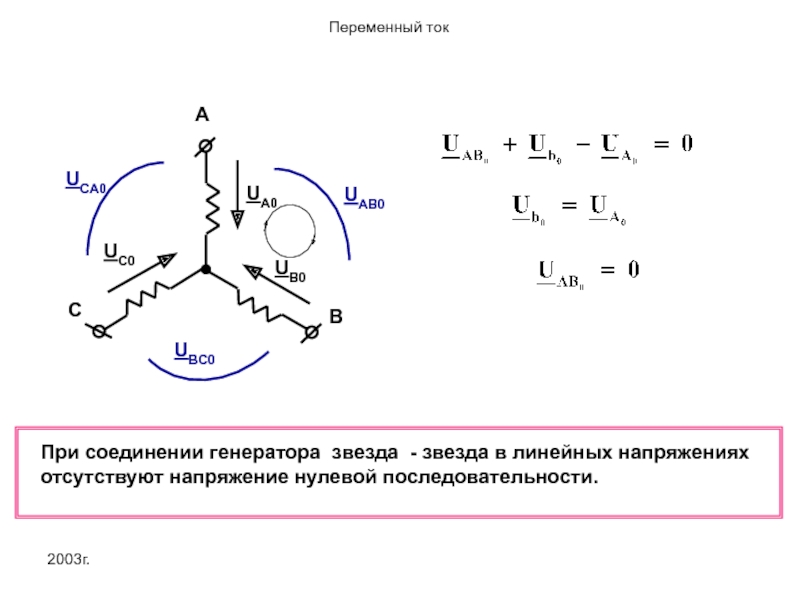
- 19. 2003г. При соединении генератора звездa - звезда
- 20. 2003г.
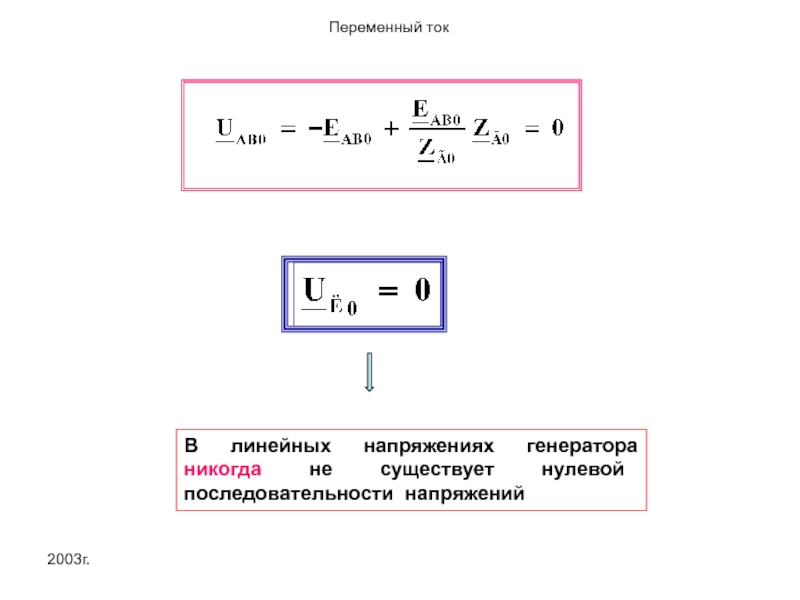
- 21. 2003г. В линейных напряжениях генератора никогда не существует нулевой последовательности напряжений
- 22. 2003г. ZNД0- сопротивление нейтрали двигателя нулевой последовательности.
- 23. 2003г. В симметричном режиме нулевой последовательности комплексные
- 24. 2003г. Выводы 1.При соединении звезда –
- 25. 2003г. Расчет простейших электрических цепей методом симметричных
- 26. 2003г. 1.По ниже приведенным формулам рассчитываем симметричные
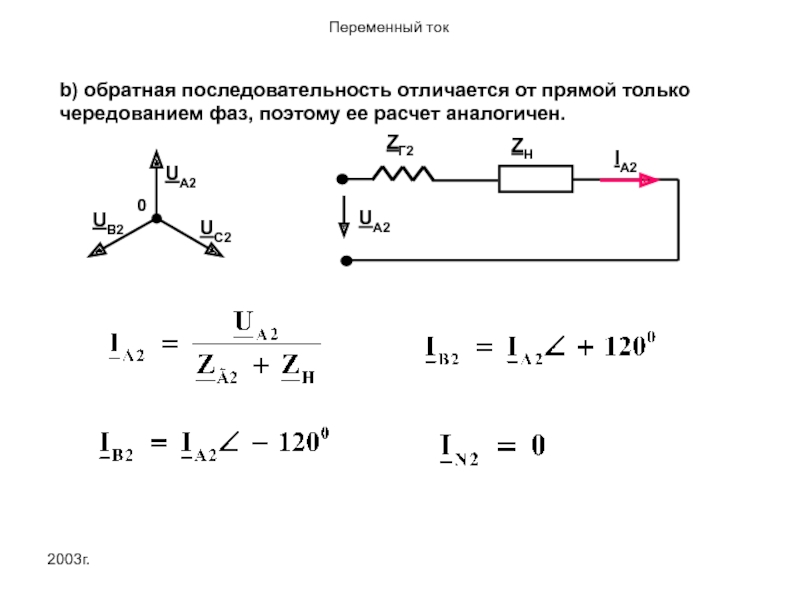
- 27. 2003г. ZH
- 28. 2003г. b) обратная последовательность отличается от прямой только чередованием фаз, поэтому ее расчет аналогичен.
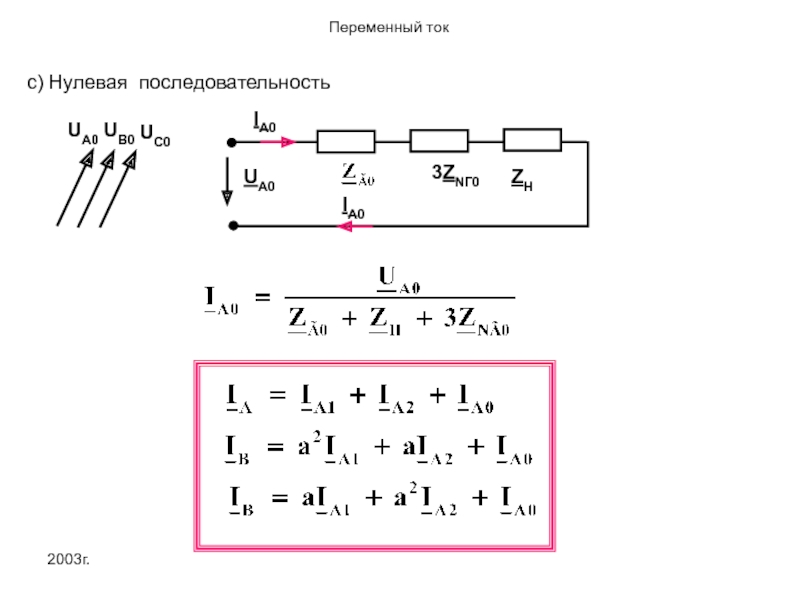
- 29. 2003г. c) Нулевая последовательность UA0 UB0 UC0
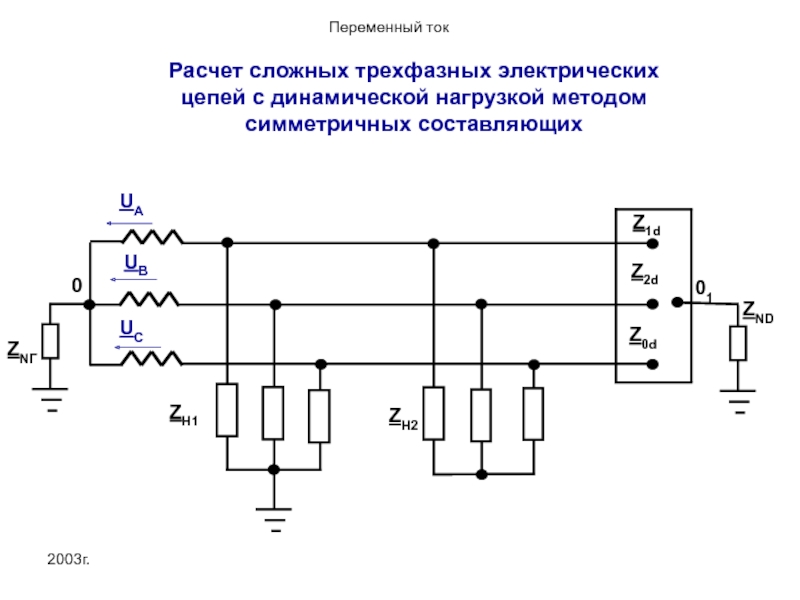
- 30. 2003г. Расчет сложных трехфазных электрических цепей с динамической нагрузкой методом симметричных составляющих
- 31. 2003г. Задана несимметричная система фазных напряжений генератора
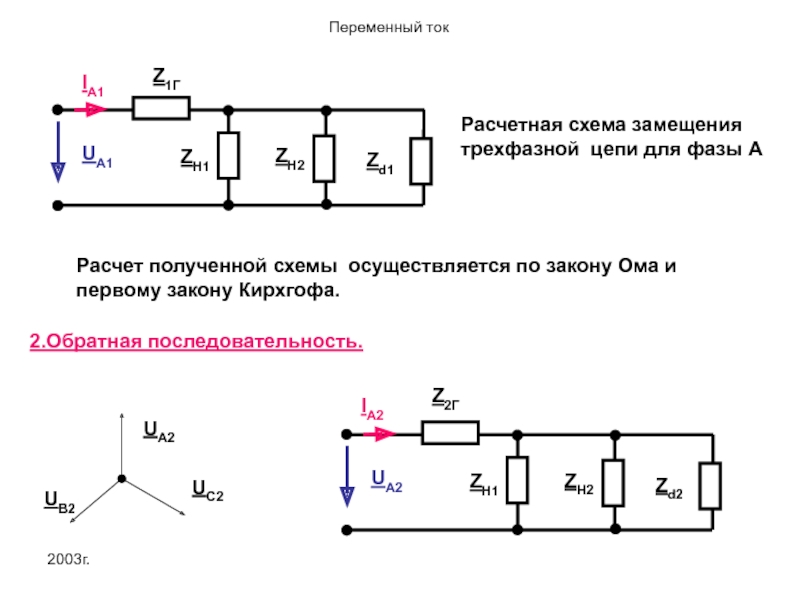
- 32. 2003г. Z1Г Расчетная схема замещения трехфазной цепи
- 33. 2003г. Расчет схемы обратной последовательности принципиально не
- 34. 2003г.
- 35. 2003г. Рассмотрим цепь с поперечным участком несимметрии
- 36. 2003г. Анализ проводим при условии, что система
- 37. 2003г. Несимметричную систему ЭДС несимметричного участка раскладываем
- 38. 2003г. Рассмотрим преобразованный участок. Верхняя тройка ЭДС образует систему прямой последовательности . UA1
- 39. 2003г. Анализ электрической цепи производится отдельно для
- 40. 2003г. H.O 1.
- 41. 2003г. 2). Проанализируем работу цепи под воздействием
- 42. 2003г. 3). Нулевая последовательность. Цепь находится под
- 43. 2003г. Z0Э UA0 IA0 3. Система уравнений для эквивалентных схем 1.
- 44. 2003г. В системе (1)шесть неизвестных величин UA1,UA2,UA0,IA1,IA2,IA0.
- 45. 2003г. Запишем систему уравнений для схемы Рис.2.
- 46. 2003г. Совместное решение системы (3) позволяет получить неизвестные симметричные составляющие токов и напряжений фаза А.
- 47. 2003г. Итоговая система уравнений для определения токов генератора.
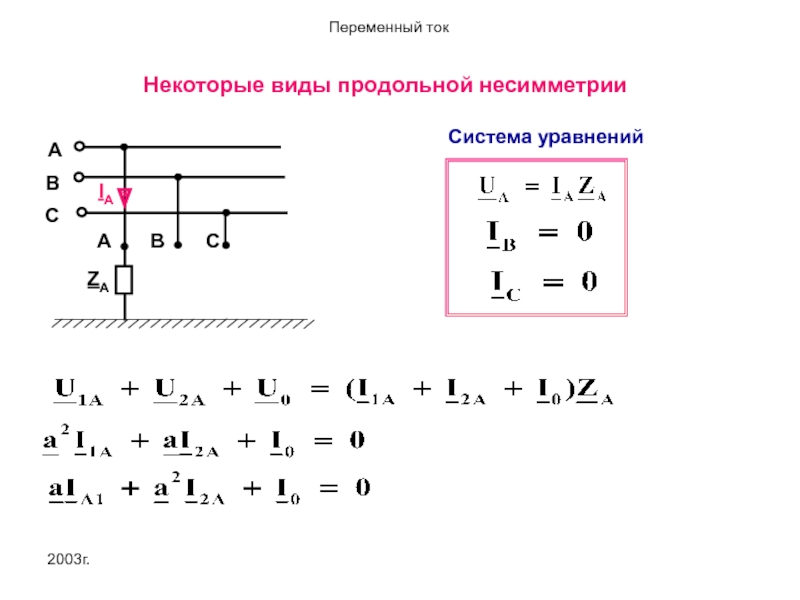
- 48. 2003г. Некоторые виды продольной несимметрии Система уравнений
- 49. 2003г. Полная система уравнений
- 50. 2003г. A B C
- 51. 2003г. Полная система уравнений (3)
- 52. 2003г. Генератор симметричен и имеет только прямую
- 53. 2003г. UAГ UBГ UCГ 0 ZNГ
- 54. 2003г. Z1Г UA1 Уравнение по второму закону
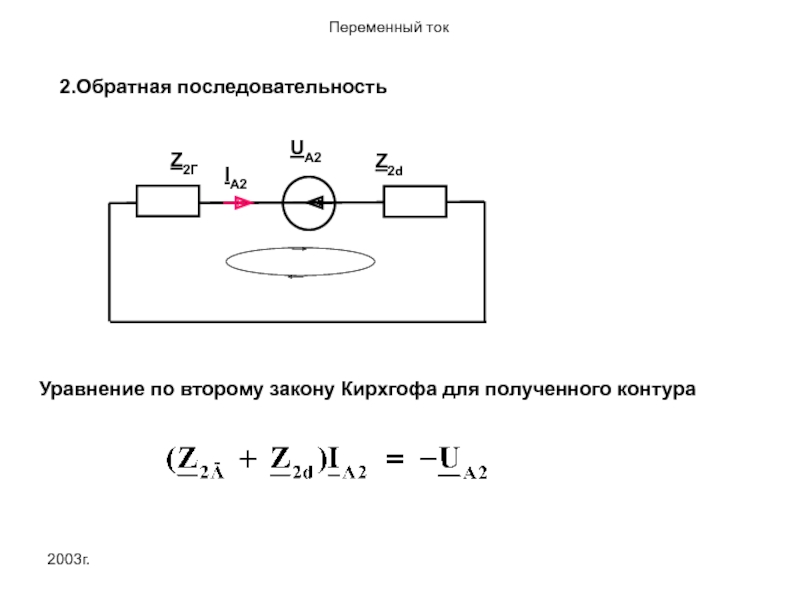
- 55. 2003г. 2.Обратная последовательность Уравнение по второму закону Кирхгофа для полученного контура
- 56. 2003г. 3.Нулевая последовательность Eг
- 57. 2003г. Система уравнений для трехфазной электрической цепи
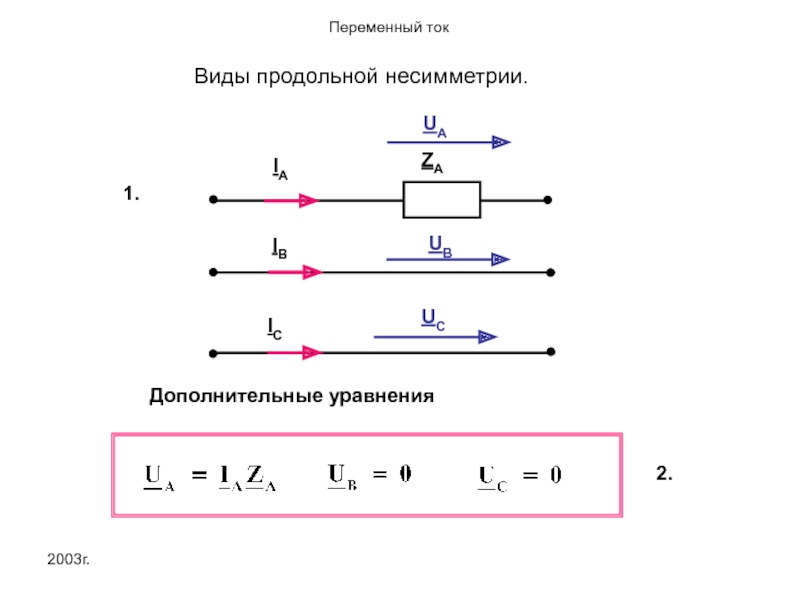
- 58. 2003г. Виды продольной несимметрии. 1. Дополнительные уравнения UA 2.
- 59. 2003г. В дополнительных уравнениях (2) токи и
- 60. 2003г. В дополнительных уравнениях (3) токи и
- 61. 2003г. В дополнительных уравнениях (4) токи и
- 62. 2003г. Произошел обрыв фазы А линии, питающей
Слайд 22003г.
Метод симметричных составляющих
1.Разложение несимметричной системы ЭДС на симметричные составляющие.
2.Сопротивления фаз
3.Расчет простых электрических цепей методом симметричных составляющих.
4.Расчет сложных электрических цепей методом симметричных составляющих.
Слайд 32003г.
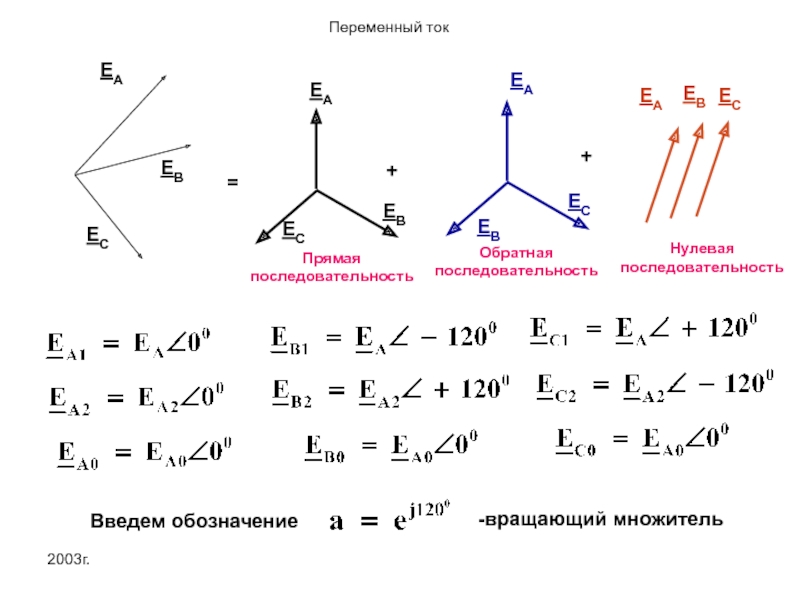
EA
EB
EC
=
+
+
EA
EB
EC
EA
EA
EB
EB
EC
EC
Прямая последовательность
Обратная последовательность
Нулевая последовательность
Введем обозначение
-вращающий множитель
Слайд 82003г.
= 0
= 0
= 3
Система уравнений для определения симметричных составляющих несимметричной системы
Слайд 92003г.
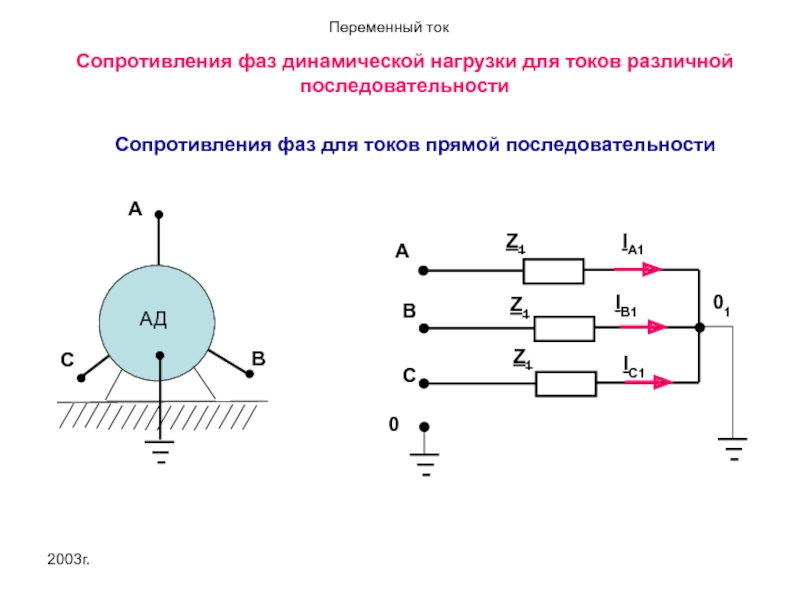
А
Сопротивления фаз динамической нагрузки для токов различной последовательности
Сопротивления фаз для токов
0
01
Слайд 102003г.
Метод симметричных составляющих
1.Разложение несимметричной системы ЭДС на симметричные составляющие.
2.Сопротивления фаз
3.Расчет простых электрических цепей методом симметричных составляющих.
4.Расчет сложных электрических цепей методом симметричных составляющих.
Слайд 112003г.
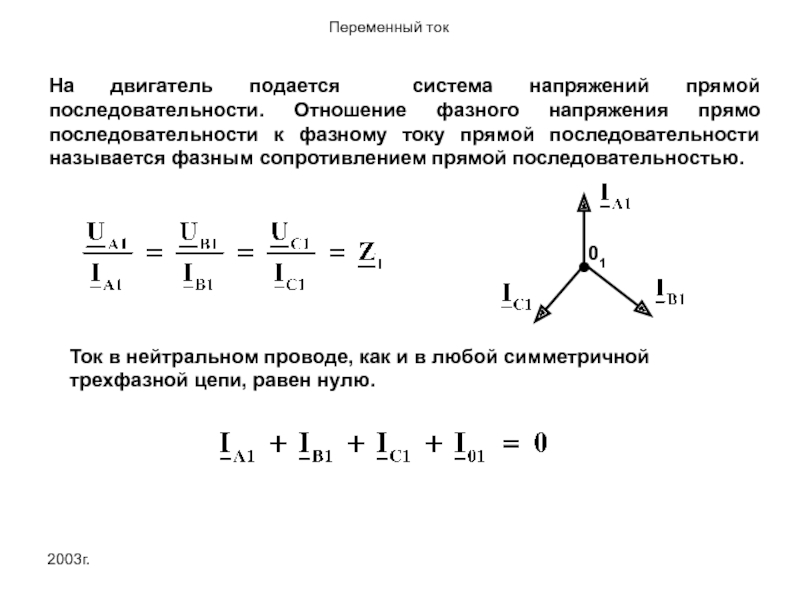
На двигатель подается система напряжений прямой последовательности. Отношение фазного напряжения прямо
Ток в нейтральном проводе, как и в любой симметричной трехфазной цепи, равен нулю.
01
Слайд 122003г.
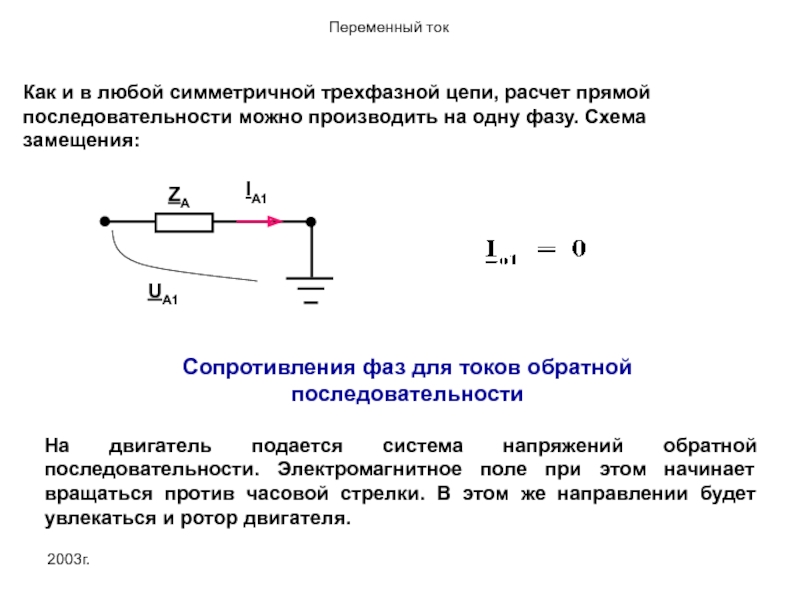
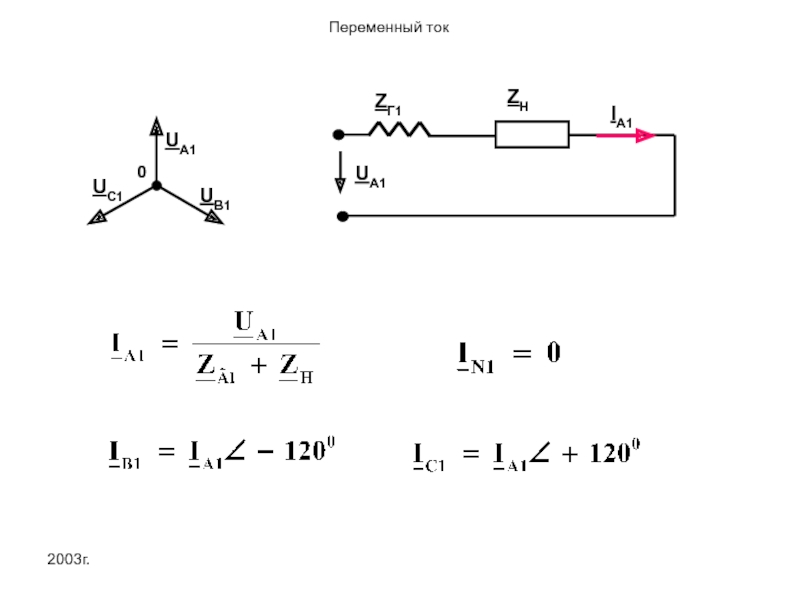
Как и в любой симметричной трехфазной цепи, расчет прямой последовательности можно
UA1
Сопротивления фаз для токов обратной последовательности
На двигатель подается система напряжений обратной последовательности. Электромагнитное поле при этом начинает вращаться против часовой стрелки. В этом же направлении будет увлекаться и ротор двигателя.
Слайд 132003г.
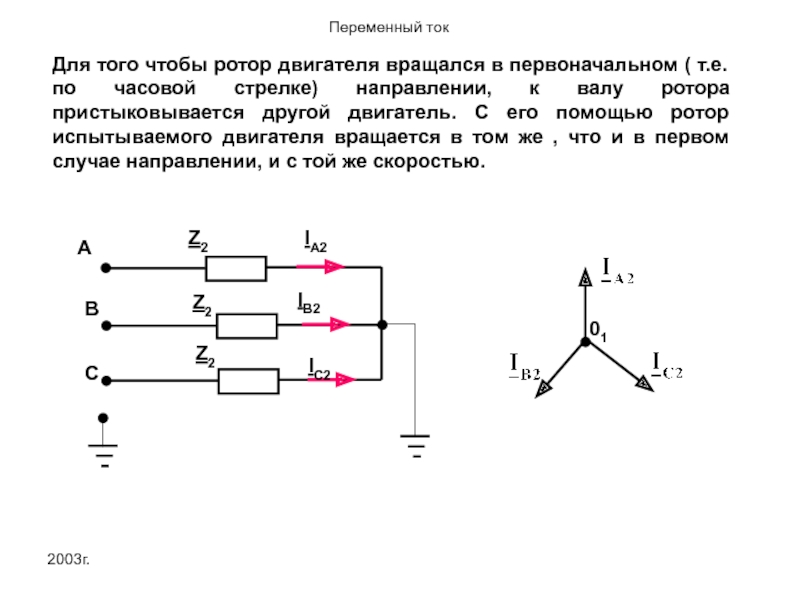
Для того чтобы ротор двигателя вращался в первоначальном ( т.е. по
Z2
Z2
Z2
A
B
C
IA2
IC2
IB2
Слайд 142003г.
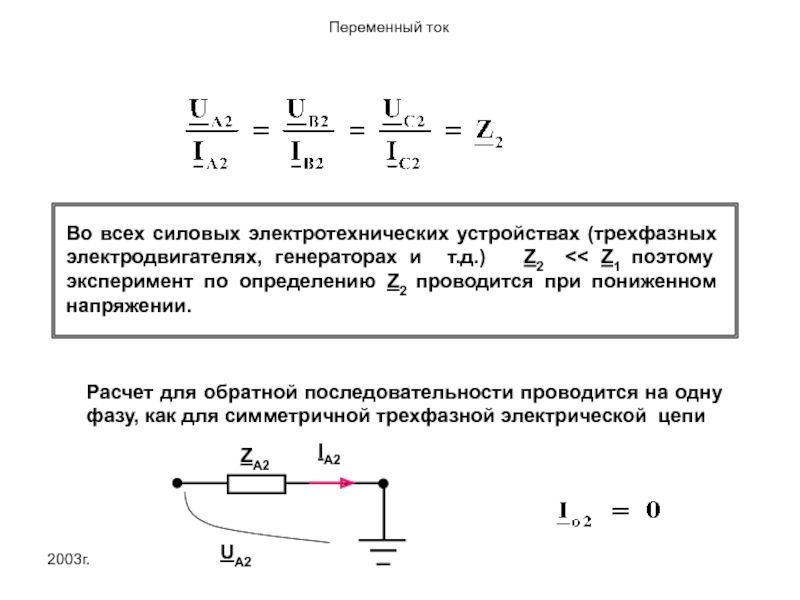
Во всех силовых электротехнических устройствах (трехфазных электродвигателях, генераторах и т.д.)
Расчет для обратной последовательности проводится на одну фазу, как для симметричной трехфазной электрической цепи
Слайд 152003г.
Сопротивления фаз для токов нулевой последовательности
Все фазы двигателя запитываются от однофазной
Слайд 162003г.
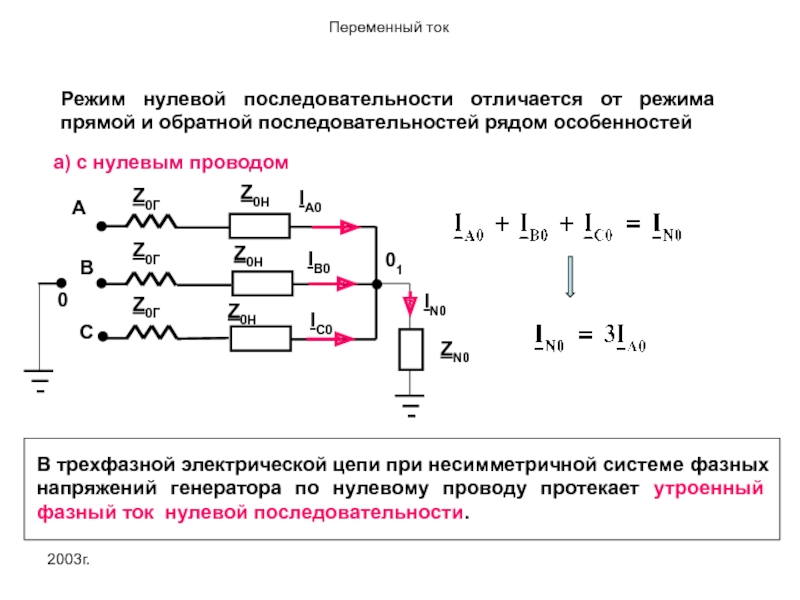
Режим нулевой последовательности отличается от режима прямой и обратной последовательностей рядом
ZN0
В трехфазной электрической цепи при несимметричной системе фазных напряжений генератора по нулевому проводу протекает утроенный фазный ток нулевой последовательности.
IN0
а) с нулевым проводом
0
01
Слайд 172003г.
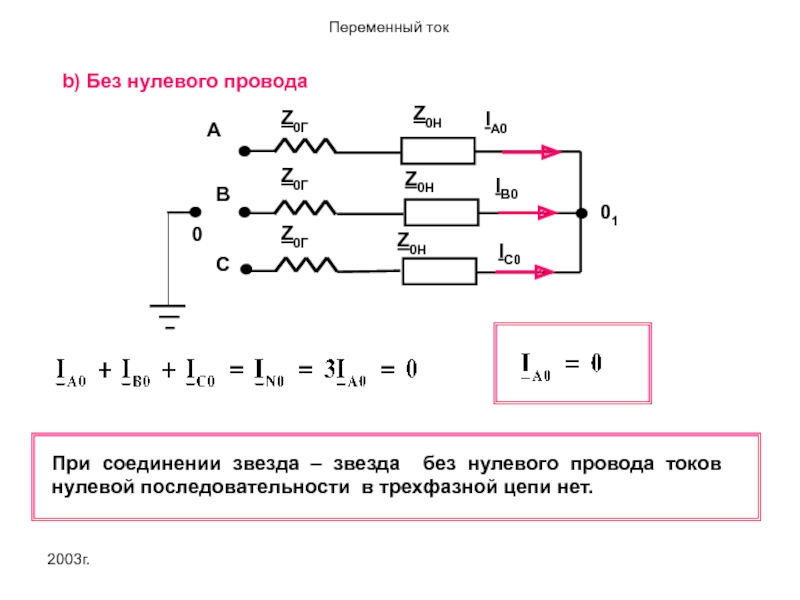
b) Без нулевого провода
При соединении звезда – звезда без нулевого провода
0
01
Слайд 182003г.
с) рассмотрим участок цепи соединенный треугольником
При соединении нагрузки треугольником токов нулевой
Слайд 192003г.
При соединении генератора звездa - звезда в линейных напряжениях отсутствуют напряжение
Слайд 212003г.
В линейных напряжениях генератора никогда не существует нулевой последовательности напряжений
Слайд 222003г.
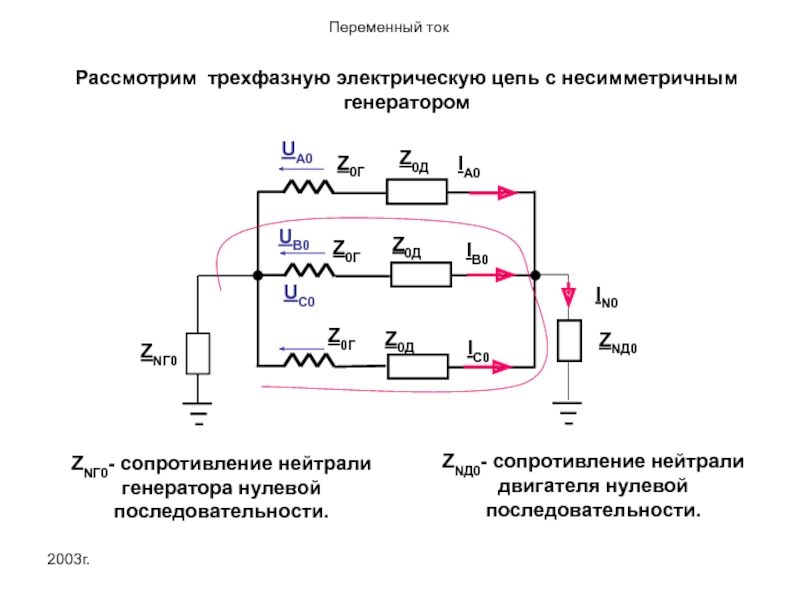
ZNД0- сопротивление нейтрали двигателя нулевой последовательности.
ZNГ0- сопротивление нейтрали генератора нулевой последовательности.
Рассмотрим
Слайд 232003г.
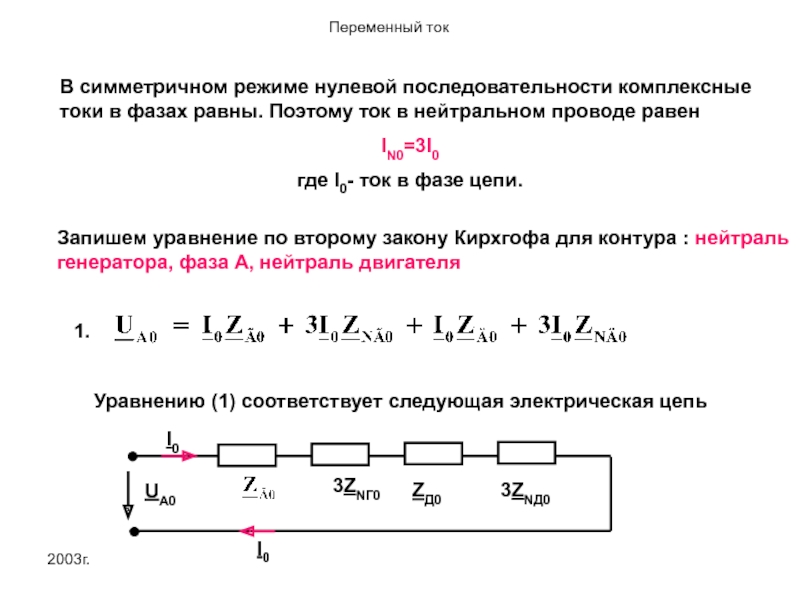
В симметричном режиме нулевой последовательности комплексные токи в фазах равны. Поэтому
IN0=3I0
где I0- ток в фазе цепи.
Запишем уравнение по второму закону Кирхгофа для контура : нейтраль генератора, фаза А, нейтраль двигателя
1.
Уравнению (1) соответствует следующая электрическая цепь
I0
Слайд 242003г.
Выводы
1.При соединении звезда – звезда без нулевого провода токов нулевой
2.При соединении нагрузки треугольником токов нулевой последовательности в ней нет.
3.При соединении генератора звездa - звезда в линейных напряжениях отсутствуют напряжение нулевой последовательности.
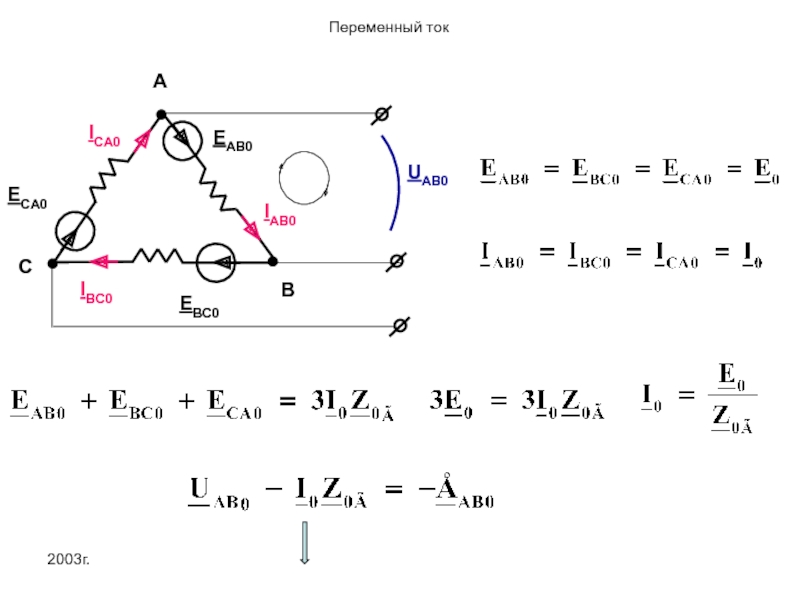
4.При соединении генератора треугольником в линейных напряжениях отсутствуют напряжение нулевой последовательности.
5.В линейных напряжениях генератора никогда не существует нулевой последовательности напряжений
6. В схеме замещения фазы для фазного тока нулевой последова-
тельности присутствует утроенное значение сопротивления
нейтрального провода.
Слайд 252003г.
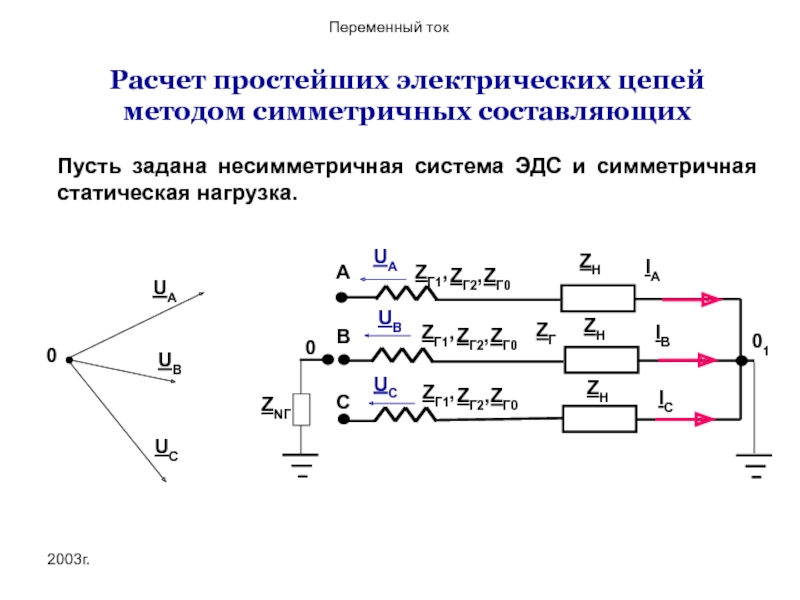
Расчет простейших электрических цепей методом симметричных составляющих
Пусть задана несимметричная система ЭДС
UB
UC
UA
0
Слайд 262003г.
1.По ниже приведенным формулам рассчитываем симметричные составляющие напряжений генератора.
2.Для каждой последовательности
а) прямая последовательность- симметричная система фазных напряжений, следовательно ее расчет не отличается от расчета обычной трехфазной цепи, работающей в симметричном режиме.
Слайд 282003г.
b) обратная последовательность отличается от прямой только чередованием фаз, поэтому ее
Слайд 302003г.
Расчет сложных трехфазных электрических цепей с динамической нагрузкой методом симметричных составляющих
Слайд 312003г.
Задана несимметричная система фазных напряжений генератора и его параметры Z1Г, Z2Г,
1.Схема прямой последовательности.
Схема прямой последовательности ничем не отличается от схем замещения фазы А в симметричных трехфазных цепях, находящихся под воздействием систем напряжений прямой последовательности
a) все нагрузки и обмотки генератора , соединенные в треугольник, эквивалентно преобразуем в звезды;
в) искусственно электрически соединяют общей шиной все нейтральные точки генераторов и приемников;
с) из полученной схемы убираем все элементы , не относящиеся к фазе А.
Слайд 322003г.
Z1Г
Расчетная схема замещения трехфазной цепи для фазы А
Расчет полученной схемы осуществляется
2.Обратная последовательность.
IA1
IA2
Слайд 332003г.
Расчет схемы обратной последовательности принципиально не отличается от расчета прямой последовательности,
3.Нулевая последовательность.
Алгоритм создания схемы:
а) убираем из схемы все нагрузки, соединенные треугольником
в) убираем из схемы все нагрузки, соединенные звездой без нулевого провода
г) если звезда имеет нулевой повод с сопротивлением ZN, то последовательно с сопротивлением фаз включают сопротивление 3ZN, положив при этом сопротивление в нейтральном проводе равным нулю.
д) удаляем из схемы все элементы, не относящиеся к фазе А.
Слайд 342003г.
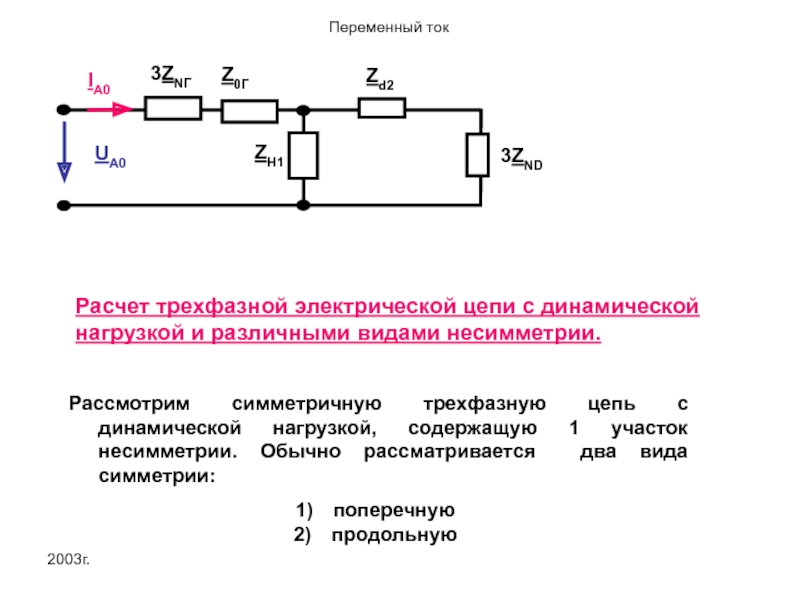
ZH1
Zd2
UA0
Z0Г
3ZNГ
3ZND
IA0
Расчет трехфазной электрической цепи с динамической нагрузкой и различными видами несимметрии.
Рассмотрим
поперечную
продольную
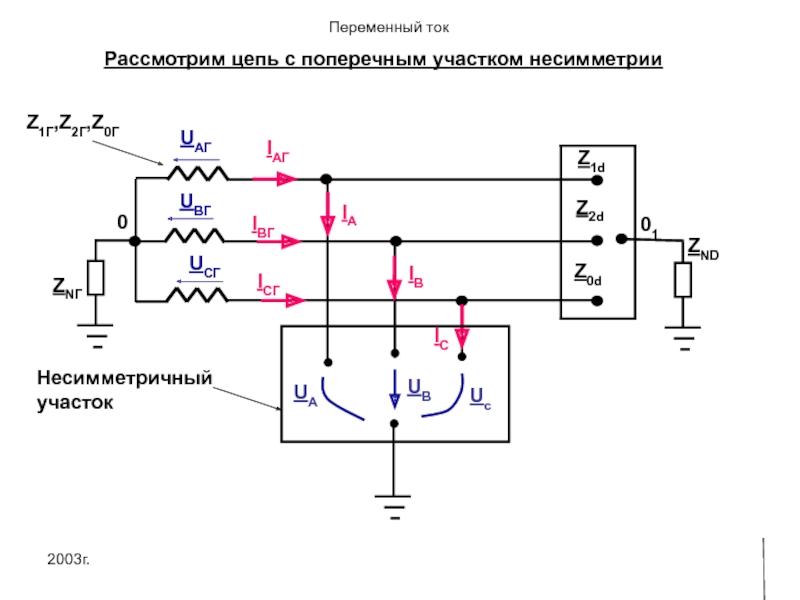
Слайд 362003г.
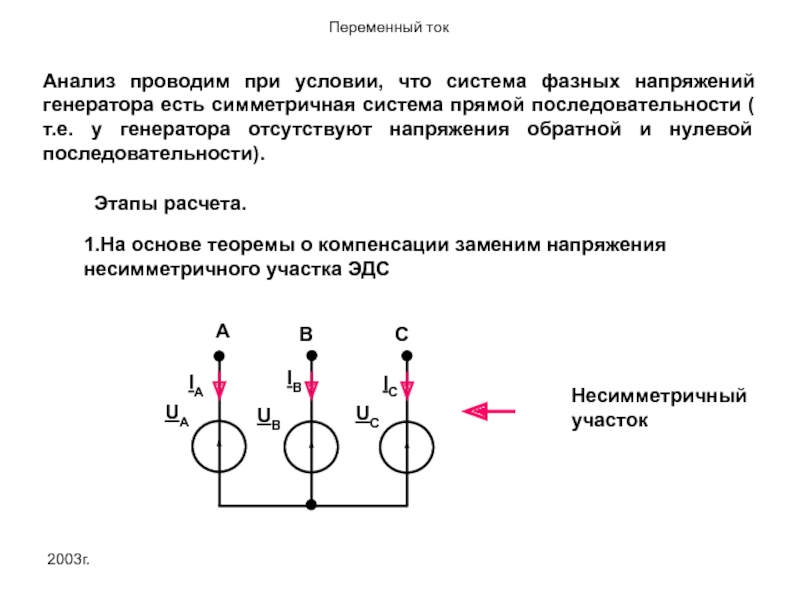
Анализ проводим при условии, что система фазных напряжений генератора есть симметричная
Этапы расчета.
1.На основе теоремы о компенсации заменим напряжения несимметричного участка ЭДС
Несимметричный участок
Слайд 372003г.
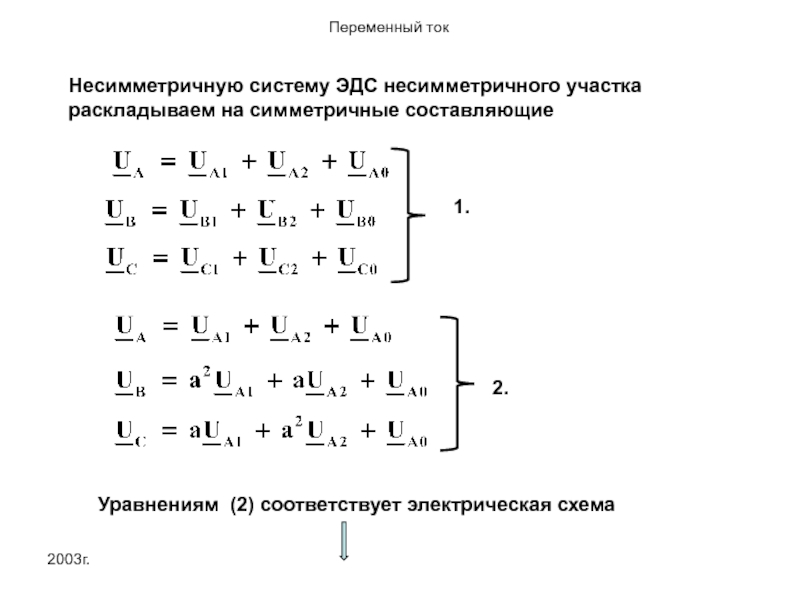
Несимметричную систему ЭДС несимметричного участка раскладываем на симметричные составляющие
1.
Уравнениям (2) соответствует
Слайд 382003г.
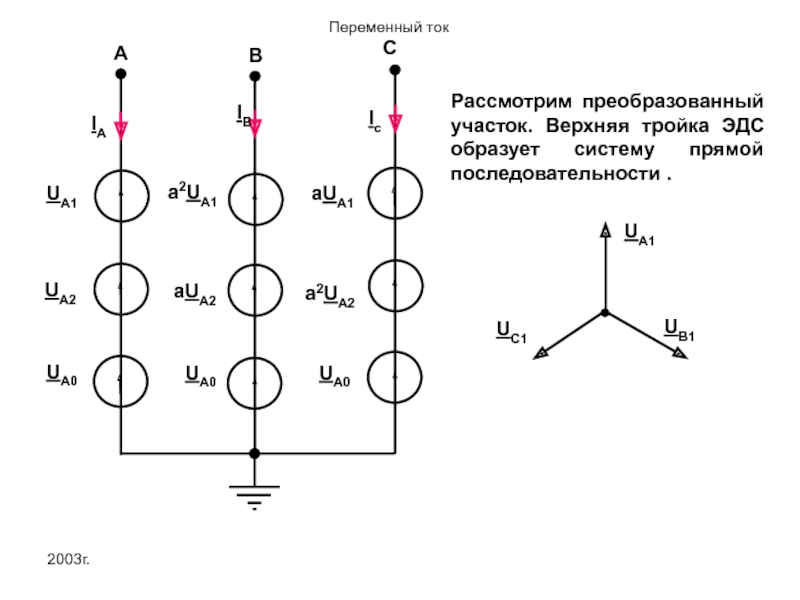
Рассмотрим преобразованный участок. Верхняя тройка ЭДС образует систему прямой последовательности .
UA1
Слайд 392003г.
Анализ электрической цепи производится отдельно для каждой последовательности
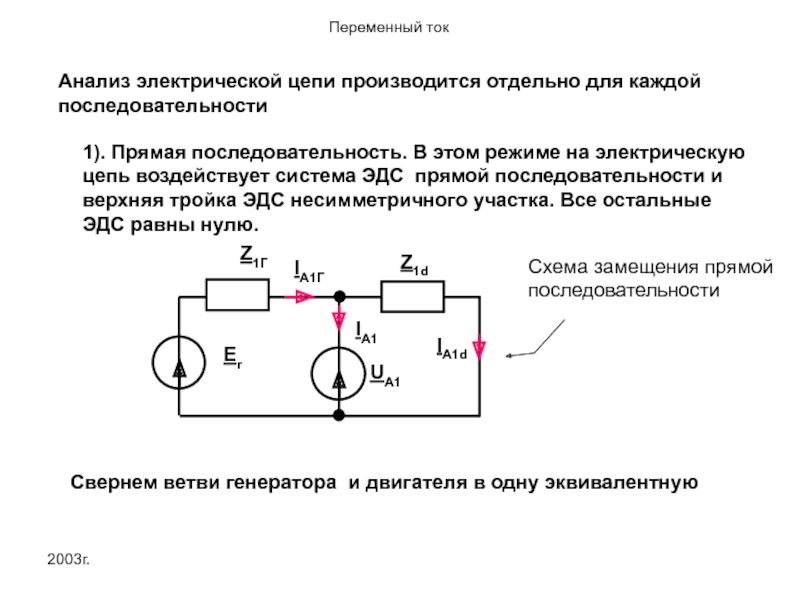
1). Прямая последовательность. В
Схема замещения прямой последовательности
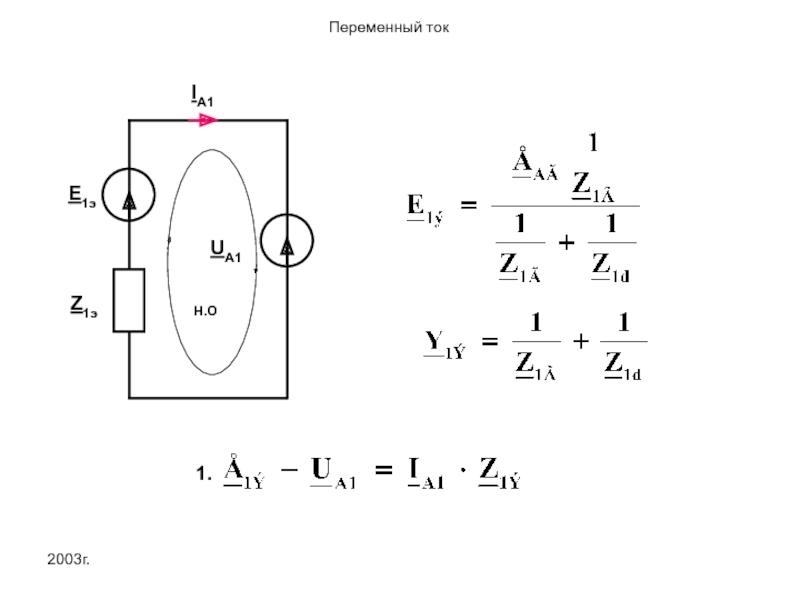
Свернем ветви генератора и двигателя в одну эквивалентную
Слайд 412003г.
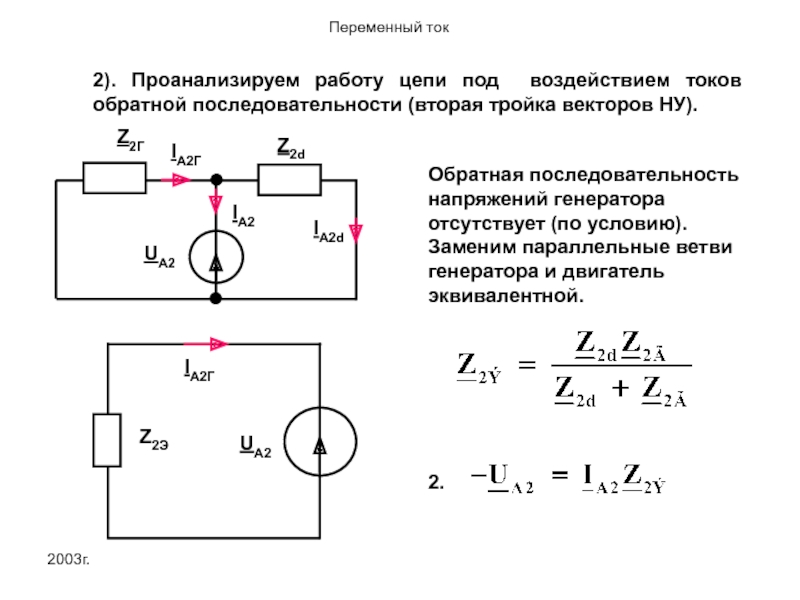
2). Проанализируем работу цепи под воздействием токов обратной последовательности (вторая тройка
IA2Г
Z2Э
UA2
Обратная последовательность напряжений генератора отсутствует (по условию). Заменим параллельные ветви генератора и двигатель эквивалентной.
2.
Слайд 422003г.
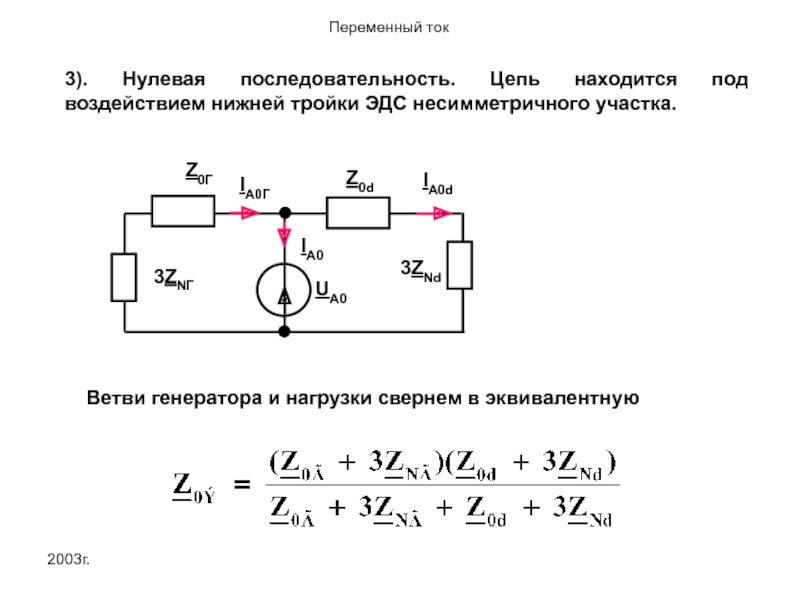
3). Нулевая последовательность. Цепь находится под воздействием нижней тройки ЭДС несимметричного
Ветви генератора и нагрузки свернем в эквивалентную
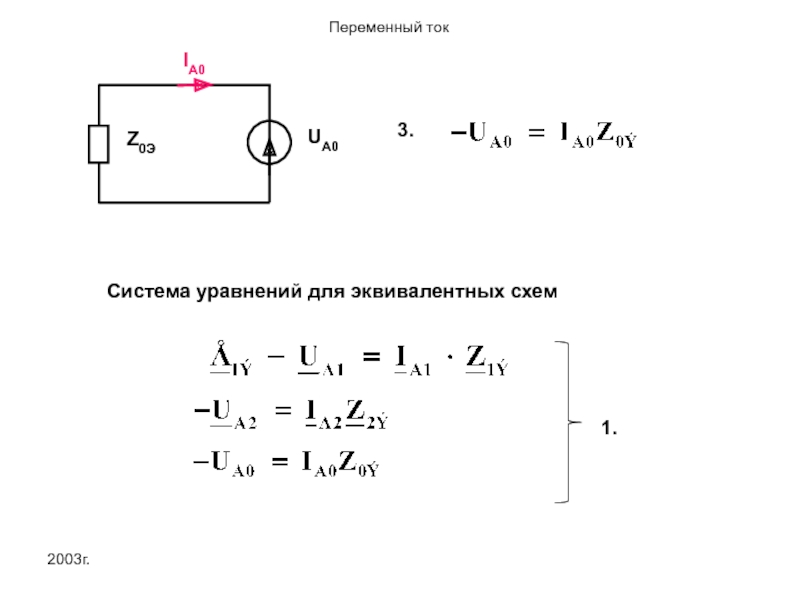
Слайд 442003г.
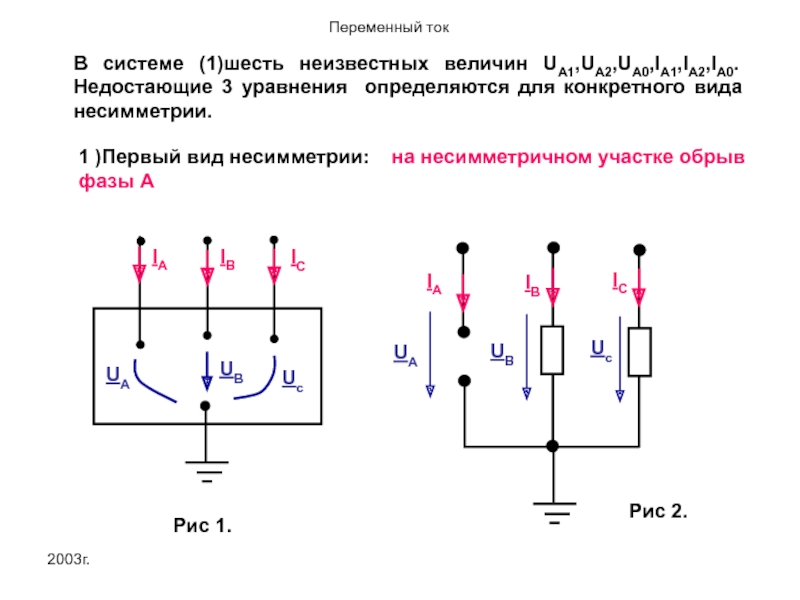
В системе (1)шесть неизвестных величин UA1,UA2,UA0,IA1,IA2,IA0. Недостающие 3 уравнения определяются для
1 )Первый вид несимметрии: на несимметричном участке обрыв фазы А
Слайд 452003г.
Запишем систему уравнений для схемы Рис.2.
1.
2.
3.
4.
5.
6.
Запишем уравнения 4,5,6, через вращающий множитель
(2)
Слайд 462003г.
Совместное решение системы (3) позволяет получить неизвестные симметричные составляющие токов и
Слайд 502003г.
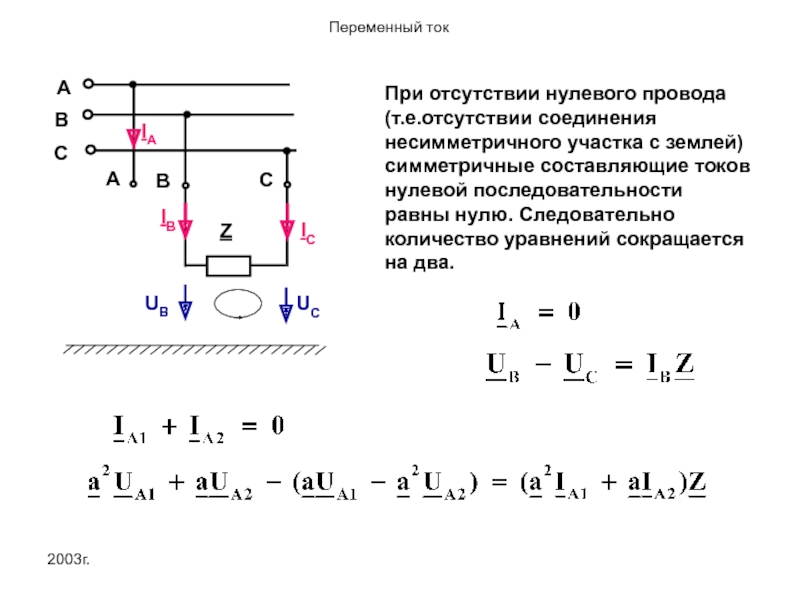
A
B
C
IA
A
C
B
IC
Z
IB
UB
UC
При отсутствии нулевого провода (т.е.отсутствии соединения несимметричного участка с землей) симметричные
Слайд 522003г.
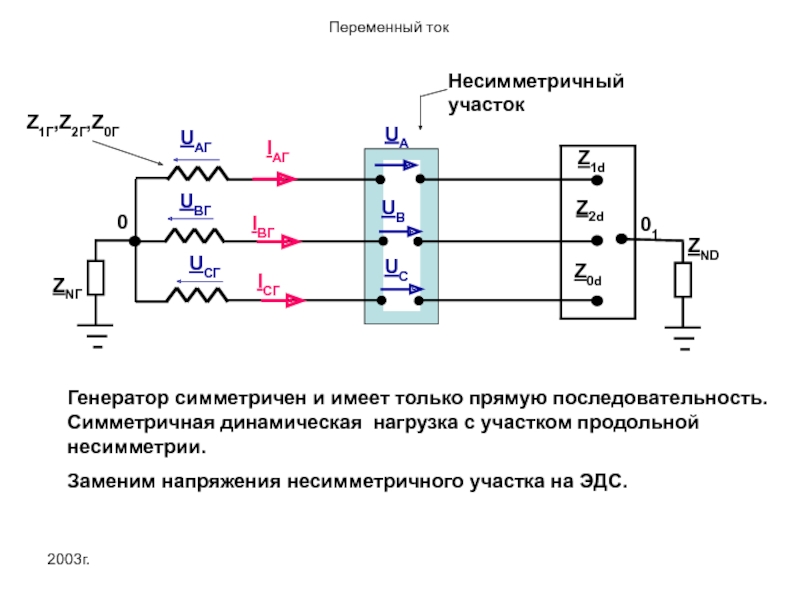
Генератор симметричен и имеет только прямую последовательность. Симметричная динамическая нагрузка с
Заменим напряжения несимметричного участка на ЭДС.
Слайд 532003г.
UAГ
UBГ
UCГ
0
ZNГ
IAГ
IBГ
IСГ
Z1Г,Z2Г,Z0Г
UA
UB
UC
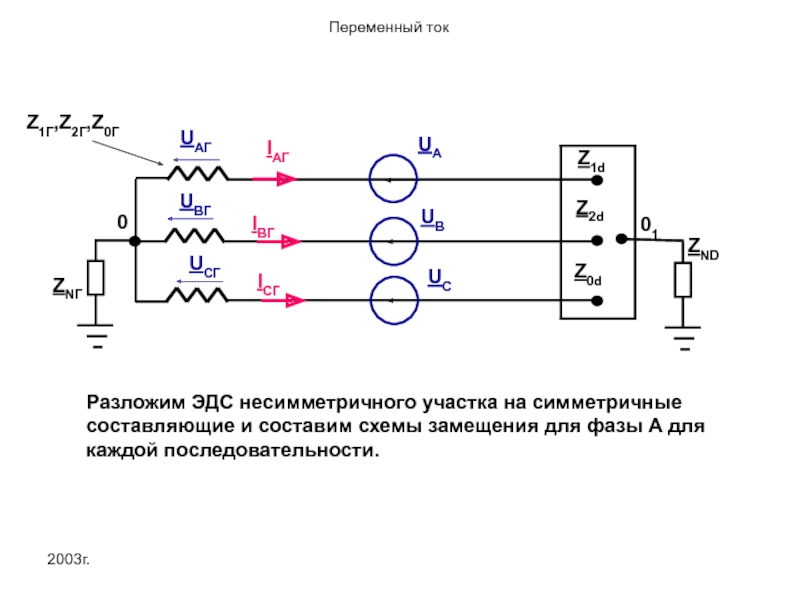
Разложим ЭДС несимметричного участка на симметричные составляющие и составим схемы замещения
Слайд 542003г.
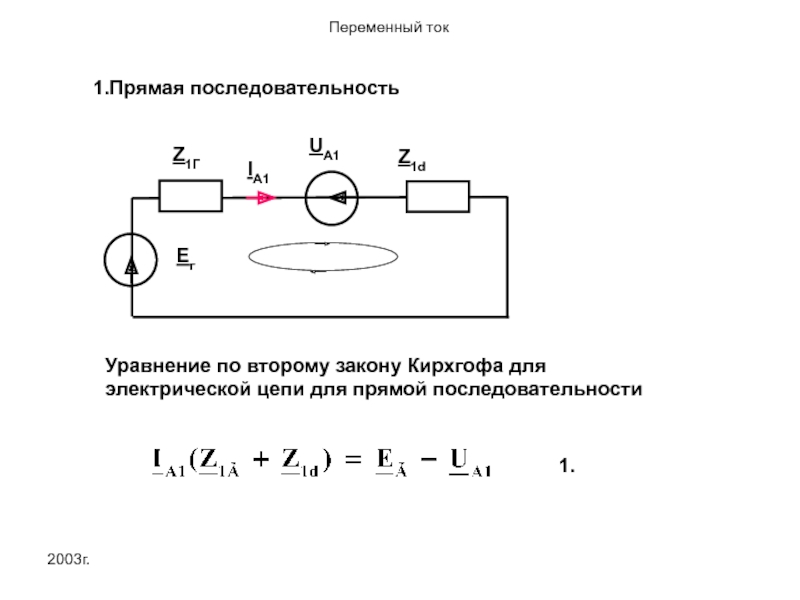
Z1Г
UA1
Уравнение по второму закону Кирхгофа для электрической цепи для прямой последовательности
1.
1.Прямая
Слайд 552003г.
2.Обратная последовательность
Уравнение по второму закону Кирхгофа для полученного контура
Слайд 562003г.
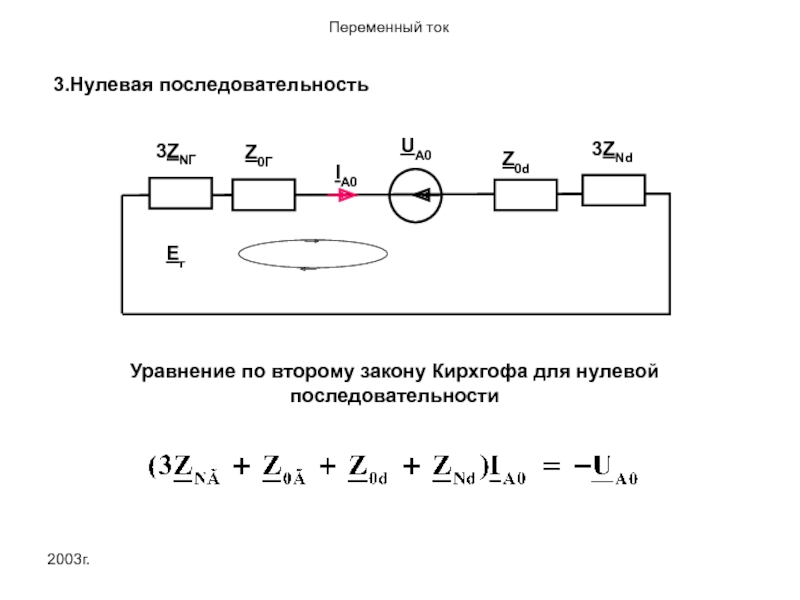
3.Нулевая последовательность
Eг
Z0d
IA0
Z0Г
UA0
3ZNГ
3ZNd
Уравнение по второму закону Кирхгофа для нулевой последовательности
Слайд 572003г.
Система уравнений для трехфазной электрической цепи с продольной несимметрией
(1)
В системе (1)
Слайд 592003г.
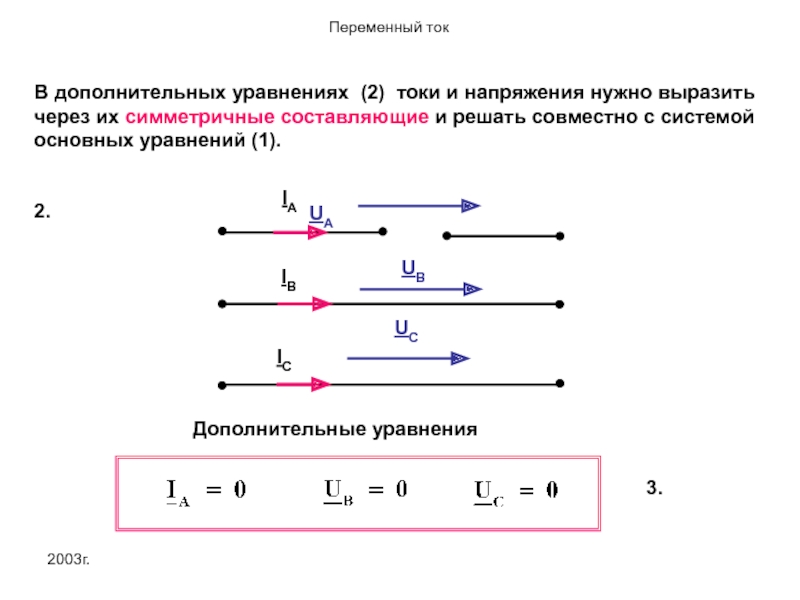
В дополнительных уравнениях (2) токи и напряжения нужно выразить через их
2.
UA
Дополнительные уравнения
3.
Слайд 602003г.
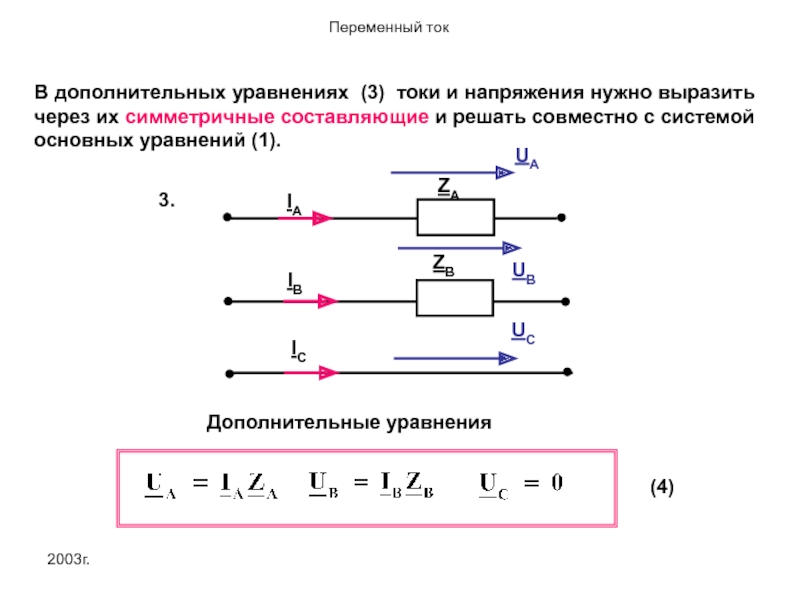
В дополнительных уравнениях (3) токи и напряжения нужно выразить через их
3.
Дополнительные уравнения
(4)
Слайд 612003г.
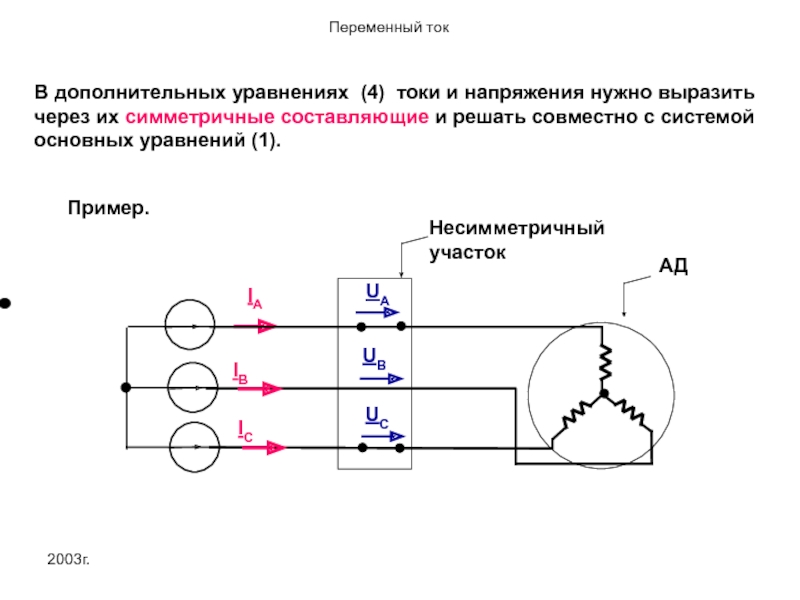
В дополнительных уравнениях (4) токи и напряжения нужно выразить через их
Пример.
Несимметричный участок
IA
IB
IС
UA
UB
UC
АД
Слайд 622003г.
Произошел обрыв фазы А линии, питающей трехфазный асинхронный двигатель. Симметричный генератор
И . Найти напряжение на несимметричном участке линии в фазе А и фазные напряжения двигателя.
Ответ: