- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Переходные процессы в линейных электрических цепях. (Лекция 6) презентация
Содержание
- 1. Переходные процессы в линейных электрических цепях. (Лекция 6)
- 2. В электрических цепях возможны включения и отключения
- 3. Первый закон. В любой ветви с индуктивностью
- 4. Второй закон. Напряжение на емкости сразу после
- 5. Допущения, применяемые при анализе переходных процессов: 1.
- 6.
- 7. В соответствии с классическим методом расчета, переходный
- 8.
- 9. Короткое замыкание в R-L цепи На
- 10.
- 11. Запишем уравнение для свободного тока в контуре,
- 12.
- 13. Постоянную интегрирования А определяем с помощью начального
- 14. На рисунке изображены кривые переходного тока в
- 15.
- 16.
- 17. До коммутации рубильник был разомкнут, и ток
- 18. На рисунке 3 изображены кривые переходного, принужденного,
- 19. Переходные процессы в цепях одним реактивным элементом
- 20.
- 21. Подставим значение свободного напряжения и производной от
- 23. Подключение R-C цепи к источнику постоянной ЭДС
- 24. В момент коммутации Постоянная интегрирования
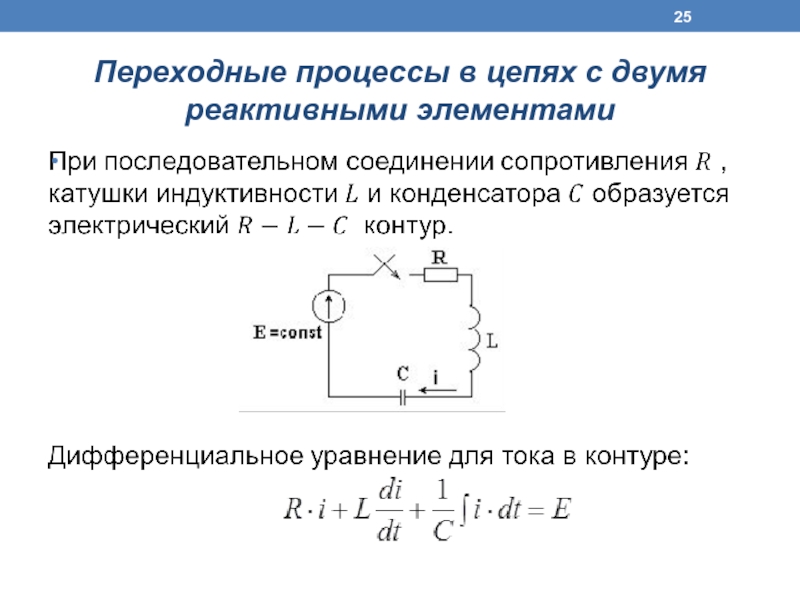
- 25. Переходные процессы в цепях с двумя реактивными элементами
- 26.
- 27. Пусть После подстановки этих
- 28. Получим: Вид корней зависит от
- 29. Спасибо за внимание!
Слайд 2В электрических цепях возможны включения и отключения отдельных ветвей, короткие замыкания
участков цепи, различного рода переключения. Любые изменения в электрических цепях можно представить в виде переключений или коммутаций. Характер коммутации указывается в схеме с помощью рубильника со стрелкой. По направлению стрелки можно судить, замыкается или размыкается рубильник.
При коммутации в цепи возникают переходные процессы, т.е. процессы перехода токов и напряжений от одного установившегося значения к другому.
Изменения токов и напряжений вызывают одновременное изменение энергии электрического и магнитного полей, связанных с элементами цепи - емкостями и индуктивностями.
Однако энергия электрического поля и энергия магнитного поля могут изменяться только непрерывно, так как скачкообразное изменение потребовало бы от источника бесконечно большой мощности. На этом рассуждении основаны законы коммутации.
При коммутации в цепи возникают переходные процессы, т.е. процессы перехода токов и напряжений от одного установившегося значения к другому.
Изменения токов и напряжений вызывают одновременное изменение энергии электрического и магнитного полей, связанных с элементами цепи - емкостями и индуктивностями.
Однако энергия электрического поля и энергия магнитного поля могут изменяться только непрерывно, так как скачкообразное изменение потребовало бы от источника бесконечно большой мощности. На этом рассуждении основаны законы коммутации.
Переходные процессы в линейных электрических цепях
Слайд 3Первый закон. В любой ветви с индуктивностью ток не может изменяться
скачком и в момент коммутации сохраняет то значение, которое он имел непосредственно перед моментом коммутации
,
где - ток в ветви с индуктивностью в момент коммутации, сразу после коммутации. Знак "+" в формуле обычно не записывается. Время переходного процесса отсчитывается от момента коммутации;
- ток в индуктивности непосредственно перед коммутацией.
,
где - ток в ветви с индуктивностью в момент коммутации, сразу после коммутации. Знак "+" в формуле обычно не записывается. Время переходного процесса отсчитывается от момента коммутации;
- ток в индуктивности непосредственно перед коммутацией.
Слайд 4Второй закон. Напряжение на емкости сразу после коммутации сохраняет то значение,
которое оно имело непосредственно перед моментом коммутации.
,
где - напряжение на емкости в момент коммутации;
- напряжение на емкости непосредственно перед моментом коммутации.
,
где - напряжение на емкости в момент коммутации;
- напряжение на емкости непосредственно перед моментом коммутации.
Слайд 5Допущения, применяемые при анализе переходных процессов:
1. Полагают, что переходный процесс длится
бесконечно большое время.
2. Считают, что замыкание и размыкание рубильника происходит мгновенно, без образования электрической дуги.
3. Принимают, что к моменту коммутации предыдущие переходные процессы в цепи закончились.
2. Считают, что замыкание и размыкание рубильника происходит мгновенно, без образования электрической дуги.
3. Принимают, что к моменту коммутации предыдущие переходные процессы в цепи закончились.
Слайд 7В соответствии с классическим методом расчета, переходный ток в ветви схемы
представляют в виде суммы принужденного и свободного токов.
где - принужденный ток, определяется в установившемся режиме после коммутации. Этот ток создается внешним источником питания.
Если в цепь включен источник постоянной ЭДС, принужденный ток будет постоянным, если в цепи действует источник синусоидальной ЭДС, принужденный ток изменяется по периодическому, синусоидальному закону;
- свободный ток, определяется в схеме после коммутации, из которой исключен внешний источник питания.
Свободный ток создается внутренними источниками питания: ЭДС самоиндукции индуктивности или напряжением заряженной емкости.
где - принужденный ток, определяется в установившемся режиме после коммутации. Этот ток создается внешним источником питания.
Если в цепь включен источник постоянной ЭДС, принужденный ток будет постоянным, если в цепи действует источник синусоидальной ЭДС, принужденный ток изменяется по периодическому, синусоидальному закону;
- свободный ток, определяется в схеме после коммутации, из которой исключен внешний источник питания.
Свободный ток создается внутренними источниками питания: ЭДС самоиндукции индуктивности или напряжением заряженной емкости.
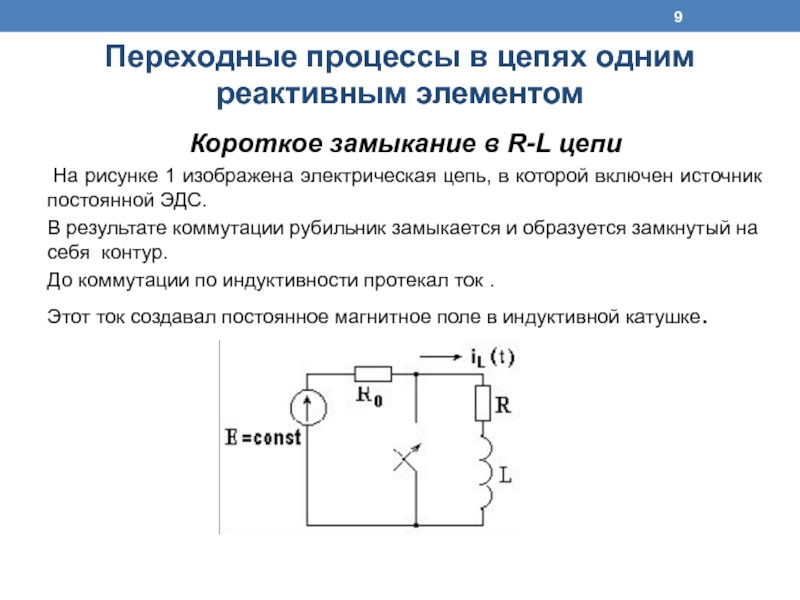
Слайд 9Короткое замыкание в R-L цепи
На рисунке 1 изображена электрическая цепь,
в которой включен источник постоянной ЭДС.
В результате коммутации рубильник замыкается и образуется замкнутый на себя контур.
До коммутации по индуктивности протекал ток .
Этот ток создавал постоянное магнитное поле в индуктивной катушке.
В результате коммутации рубильник замыкается и образуется замкнутый на себя контур.
До коммутации по индуктивности протекал ток .
Этот ток создавал постоянное магнитное поле в индуктивной катушке.
Переходные процессы в цепях одним реактивным элементом
Слайд 11Запишем уравнение для свободного тока в контуре, используя второй закон Кирхгофа:
(1)
Ищем решение этого уравнения в виде экспоненты:
Производная:
.
Слайд 13 Постоянную интегрирования А определяем с помощью начального условия.
В соответствии с
первым законом коммутации,
.
Получим: .
Напряжение на индуктивности:
.
Получим: .
Напряжение на индуктивности:
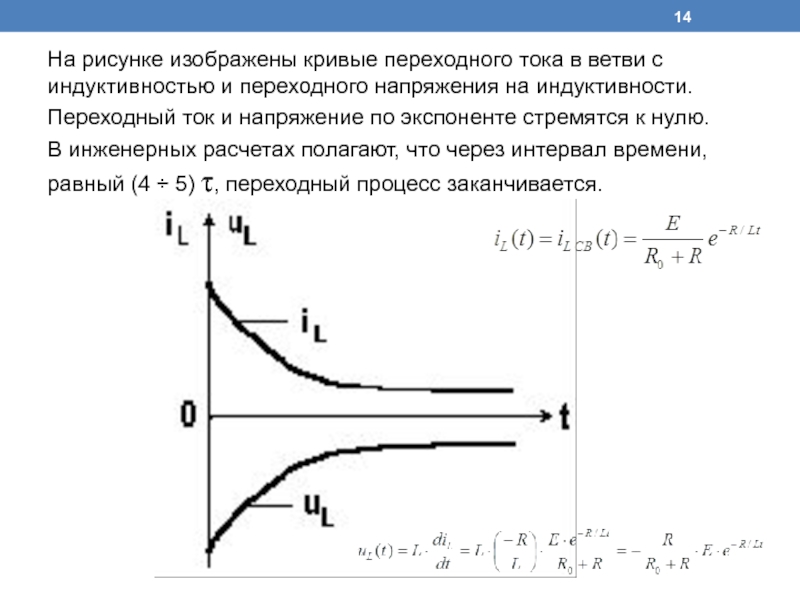
Слайд 14На рисунке изображены кривые переходного тока в ветви с индуктивностью и
переходного напряжения на индуктивности.
Переходный ток и напряжение по экспоненте стремятся к нулю.
В инженерных расчетах полагают, что через интервал времени, равный (4 ÷ 5) τ, переходный процесс заканчивается.
Переходный ток и напряжение по экспоненте стремятся к нулю.
В инженерных расчетах полагают, что через интервал времени, равный (4 ÷ 5) τ, переходный процесс заканчивается.
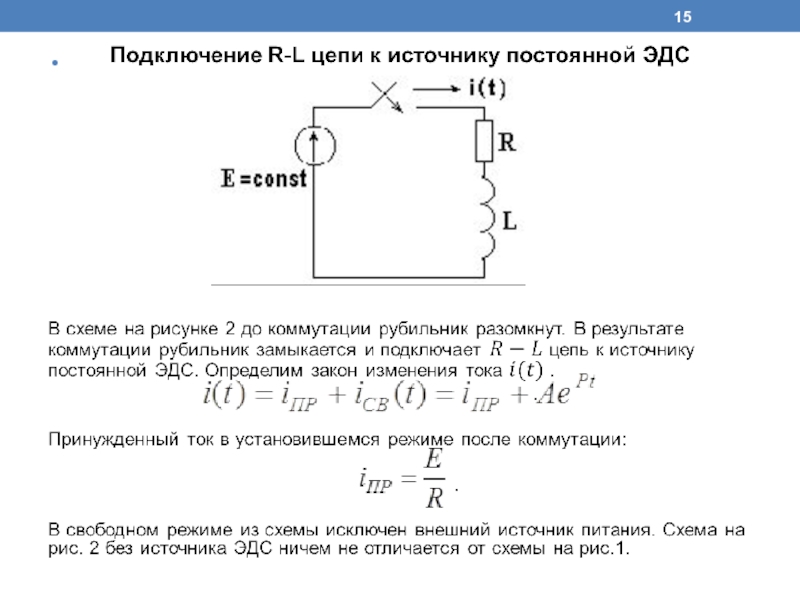
Слайд 17До коммутации рубильник был разомкнут, и ток в схеме отсутствовал. Сразу
после коммутации ток в индуктивности остается равным нулю.
.
.
.
Напряжение на индуктивности:
.
.
.
.
Напряжение на индуктивности:
.
Слайд 18На рисунке 3 изображены кривые переходного, принужденного, свободного токов и переходного
напряжения на индуктивности.
Свободный ток и напряжение на индуктивности плавно уменьшаются до нуля.
В момент коммутации свободный и принужденный токи одинаковы по абсолютной величине.
Переходный ток начинается при включении с нуля, затем возрастает, приближаясь к установившемуся постоянному значению.
Свободный ток и напряжение на индуктивности плавно уменьшаются до нуля.
В момент коммутации свободный и принужденный токи одинаковы по абсолютной величине.
Переходный ток начинается при включении с нуля, затем возрастает, приближаясь к установившемуся постоянному значению.
Слайд 21Подставим значение свободного напряжения и производной от напряжения
в уравнение (1).
Уравнение называется характеристическим.
- корень характеристического уравнения;
- постоянная времени переходного процесса;
Уравнение называется характеристическим.
- корень характеристического уравнения;
- постоянная времени переходного процесса;
Слайд 22
Переходный ток и переходное напряжение на конденсаторе по показательному закону уменьшаются
до нуля
Слайд 23Подключение R-C цепи к источнику постоянной ЭДС
Полагаем, что до коммутации
конденсатор не заряжен, напряжение на нем .
В результате коммутации рубильник замыкается, и конденсатор полностью заряжается.
Принужденное напряжение на емкости равно ЭДС источника питания:
Переходное напряжение:
В результате коммутации рубильник замыкается, и конденсатор полностью заряжается.
Принужденное напряжение на емкости равно ЭДС источника питания:
Переходное напряжение:
Слайд 24В момент коммутации
Постоянная интегрирования
В соответствии со
вторым законом коммутации
Переходное напряжение:
Переходный ток:
Кривые напряжений и тока изображены на рисунке:
Переходное напряжение:
Переходный ток:
Кривые напряжений и тока изображены на рисунке:
Слайд 27Пусть
После подстановки этих выражений в уравнение (3) получим характеристическое
уравнение:
Характеристическое уравнение имеет два корня:
где - коэффициент затухания;
- угловая резонансная частота контура без потерь.
Характеристическое уравнение имеет два корня:
где - коэффициент затухания;
- угловая резонансная частота контура без потерь.
Слайд 28Получим:
Вид корней зависит от отношения
где
- характеристическое или волновое сопротивление контура;
- добротность контура.
- добротность контура.