механические свойства
кристаллов.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дислокации в кристаллах. Влияние дислокаций на механические свойства кристаллов презентация
Содержание
- 1. Дислокации в кристаллах. Влияние дислокаций на механические свойства кристаллов
- 2. - линейные дефекты -
- 3. Классификация дефектов по их размерности Классификацию
- 4. Линейные дефекты: дислокации Лат. dislocatio - смещение,
- 5. Пластическая деформация кристаллов A x Для малых
- 6. F = - dU/dx Модель Френкеля
- 7. Типы дислокаций: Краевые дислокации -
- 8. Геометрия дислокаций Создание напряженного состояния в месте внедрения дополнительной полуплоскости
- 9. Ядро дислокации (??) - сильные искажения решетки
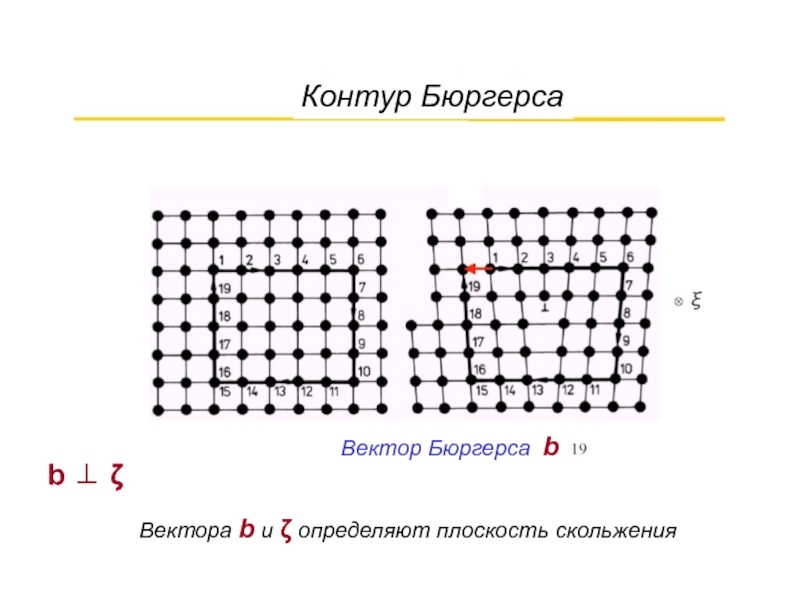
- 10. Контур Бюргерса Вектор Бюргерса b b ⊥ ζ Вектора b и ζ определяют плоскость скольжения
- 11. Определение дислокации: Дислокацией называется линейный дефект
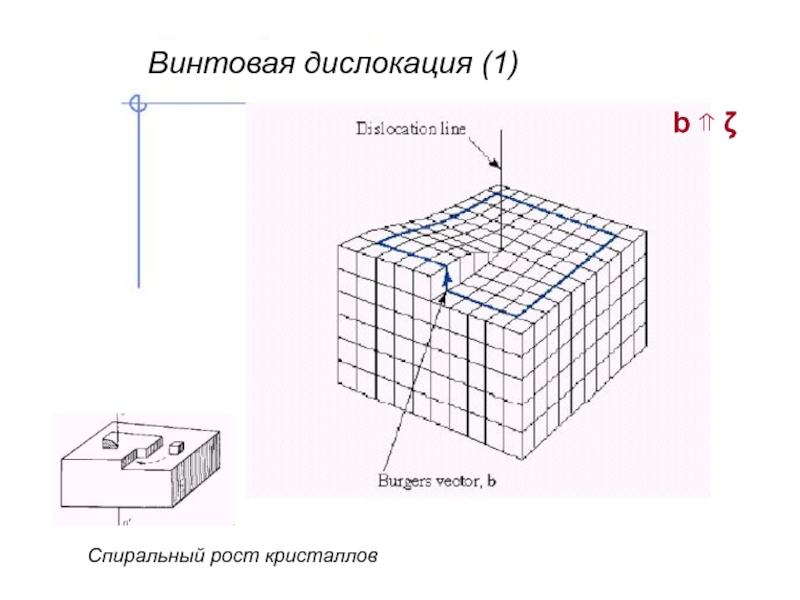
- 12. Спиральный рост кристаллов Винтовая дислокация (1) b ⇑ ζ
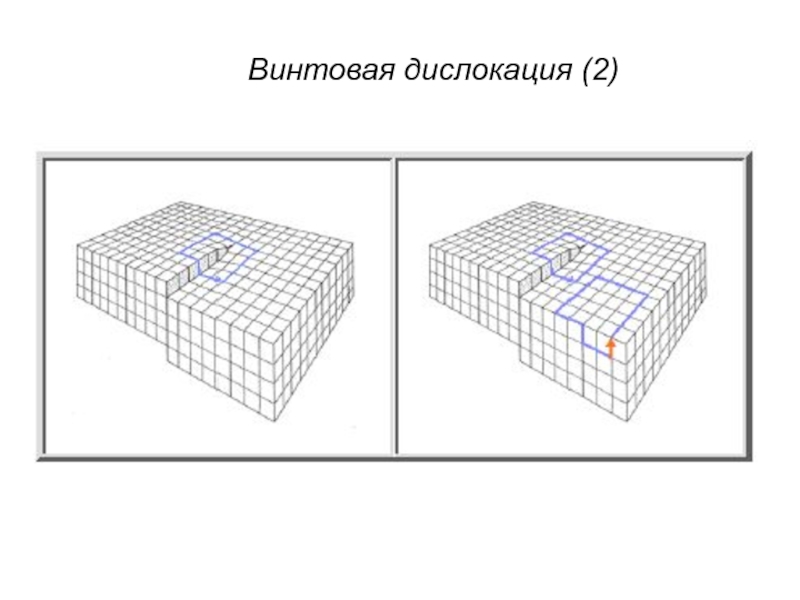
- 13. Винтовая дислокация (2)
- 15. (a) Perfect simple-cubic crystal. (b) Displacement
- 16. Смешанная дислокация Сдвиг в плоскости скольжения По
- 17. Разложение вектора Бюргерса на составляющие для смешанной дислокации
- 18. Описание смешанной дислокации
- 19. Oscar Rodríguez de la Fuente, Ph.D. Thesis, UCM Screw dislocation Edge dislocation Dislocations
- 21. Свойства вектора Бюргерса Finish-start/ right hand
- 22. К определению вектора Бюргерса (1)
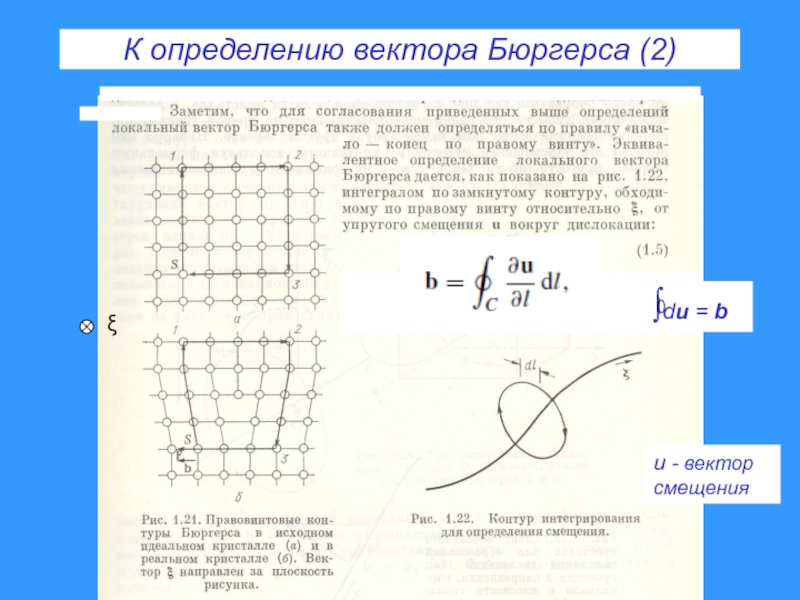
- 23. К определению вектора Бюргерса (2) ∫du
- 24. Вектор Бюргерса является аксиальным
- 25. Свойства дислокаций Дислокационная линия не может закончиться
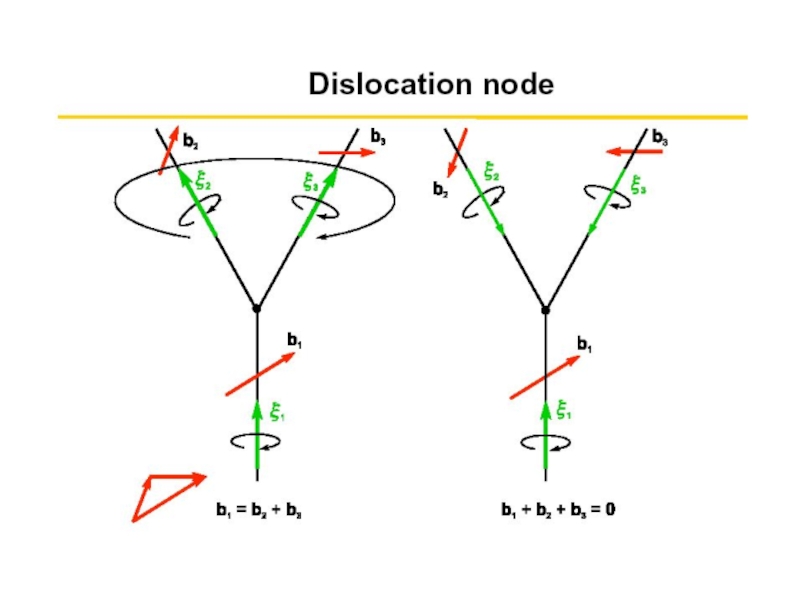
- 26. Свойства дислокаций ∑ bi = 0
- 27. Для доказательства этого утверждения предполо-
- 28. b1 ∑ bi = 0
- 29. Эквивалентные контуры Бюргерса
- 32. Дислокации в непрерывной упругой среде Построение Вольтерра
- 33. Образование краевой дислокации в кристалле
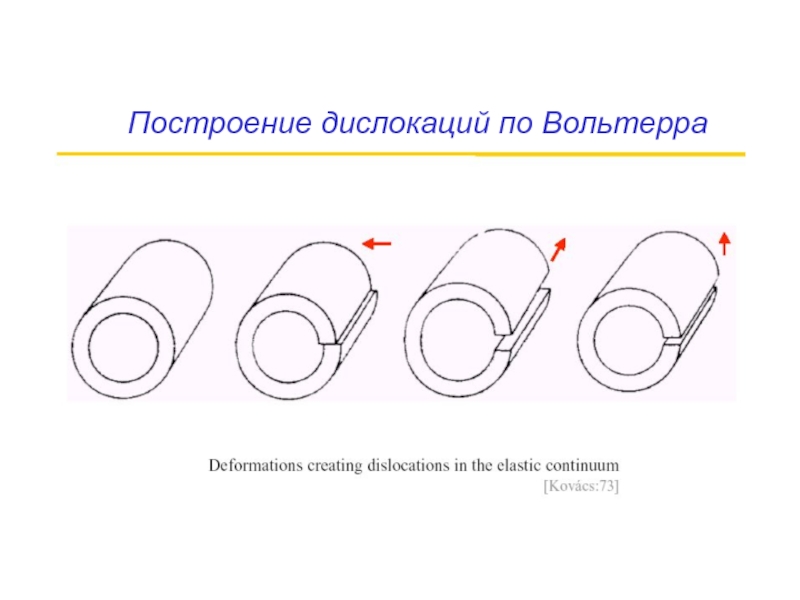
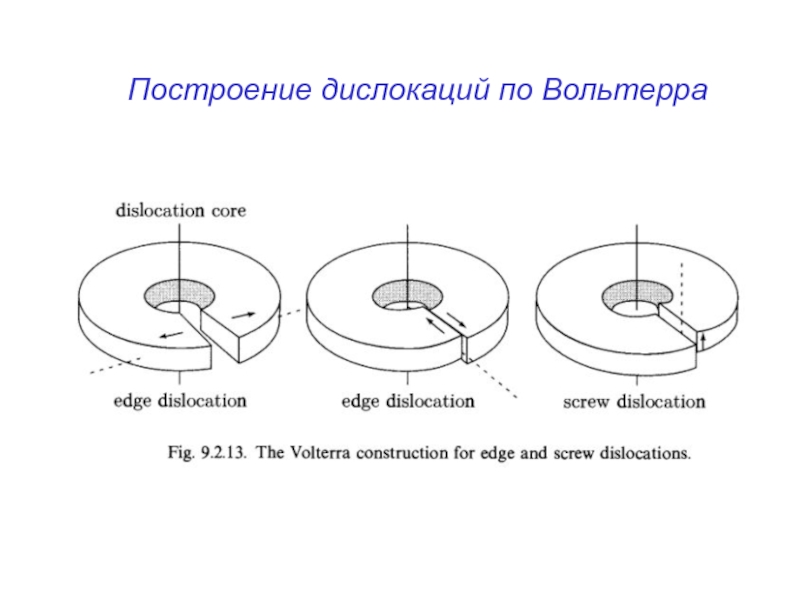
- 34. Построение дислокаций по Вольтерра
- 35. Построение дислокаций по Вольтерра
- 36. Образование дислокационных петель
- 37. Диссоциация дислокаций Задача линейной теории упругости
- 38. Движение дислокаций является основным механизмом пластической деформации кристаллов исключения: нитевидные кристаллы, углеродные нанотрубки
- 39. Dislocations make slip 1000 times easier, which
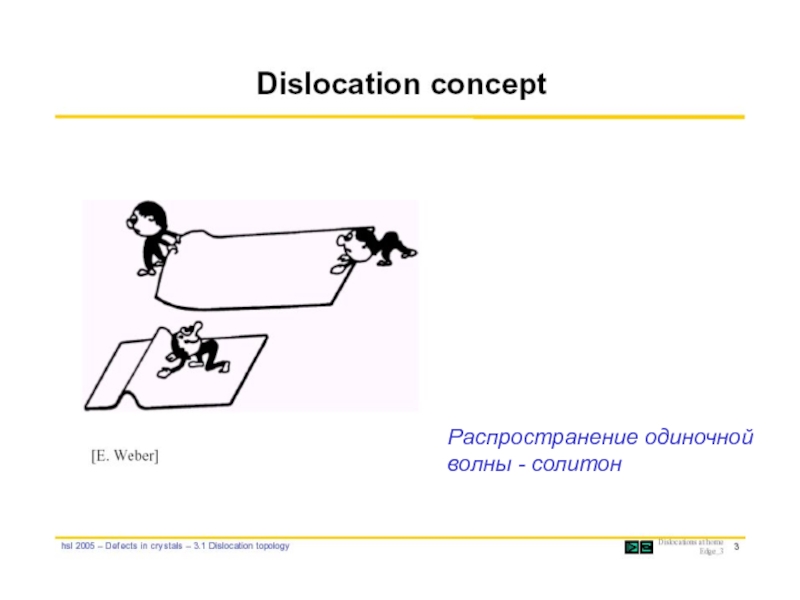
- 40. Распространение одиночной волны - солитон
- 41. TEM - 1949 (!) transmission electron
- 42. Движение дислокаций как механизм пластической деформации σ = 10-4 G
- 43. Образование ступенек скольжения
- 44. Дислокационный механизм пластической деформации
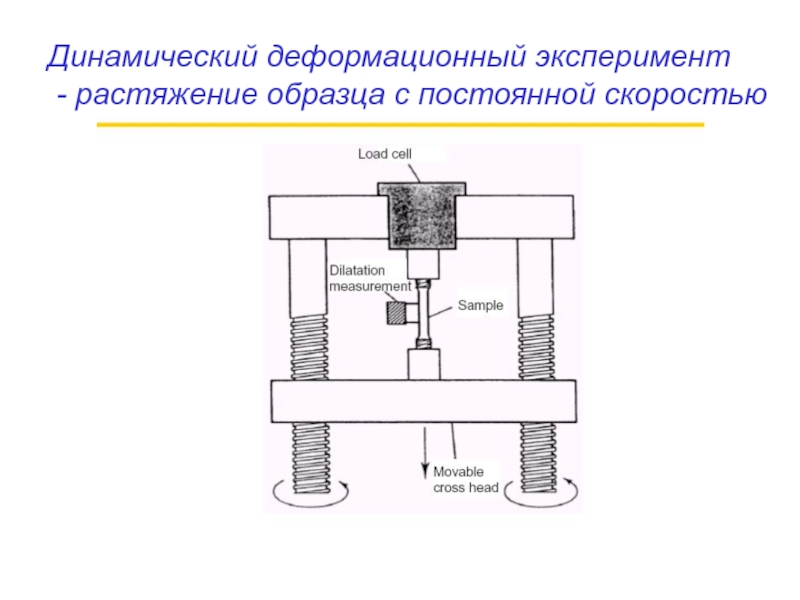
- 45. Динамический деформационный эксперимент - растяжение образца с постоянной скоростью
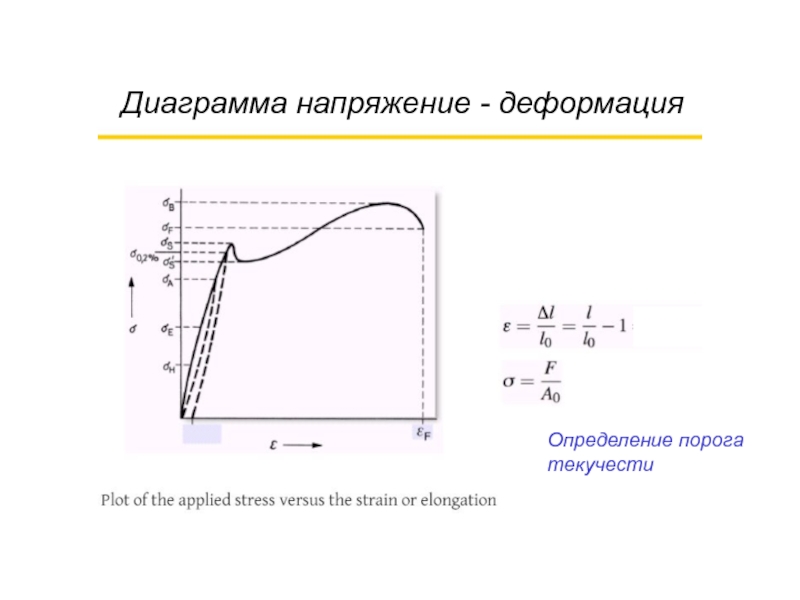
- 46. Диаграмма напряжение - деформация Определение порога текучести
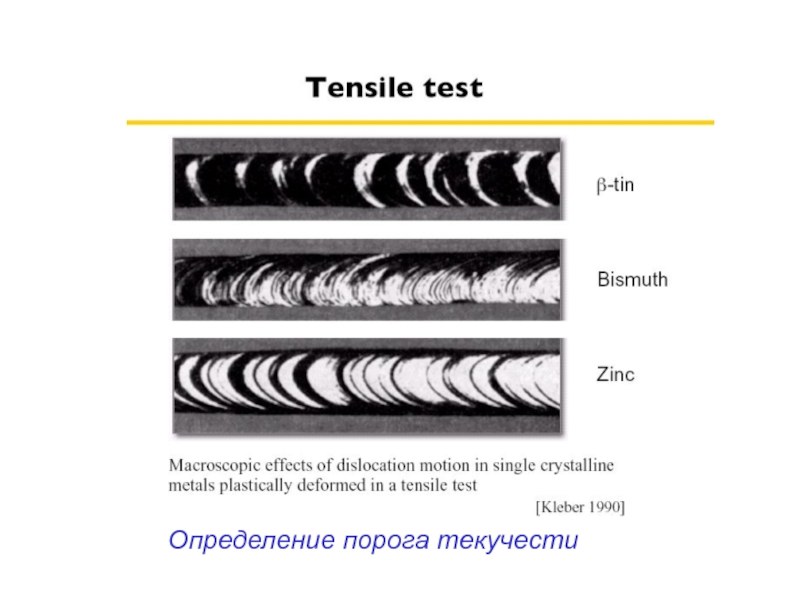
- 47. Определение порога текучести
- 48. Three common crystal structures in metals: Face
- 49. Совершенные кристаллы (?) A silicon ingot is
- 50. ρ -1/2 Плотность дислокаций Определение плотности дислокаций
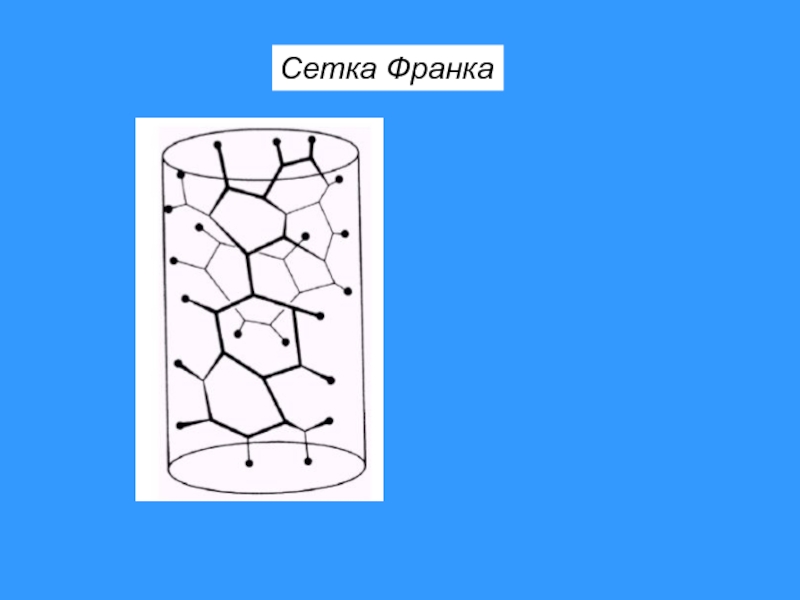
- 51. Сетка Франка
- 52. Плотность дислокаций (2)
- линейные дефекты - дислокации, типы дислокаций в
кристаллах, дислокационные реакции
- напряжения, создаваемые дислокациями в кристаллах, энергия
дислокаций,
Слайд 1Профессор Б.И.Островский
Физика реального кристалла
ostr@cea.ru
6. Дислокации в кристаллах. Влияние
дислокаций на
Слайд 2 - линейные дефекты - дислокации, типы дислокаций в
кристаллах, дислокационные реакции
- напряжения, создаваемые дислокациями в кристаллах, энергия
дислокаций, взаимодействие дислокаций друг с другом и с
точечными дефектами
- движение дислокаций, пластическая деформация в кристаллах,
размножение дислокаций, активационные барьеры и стопоры,
прочность кристаллов
- скопления дислокаций, дислокационные стенки, малоугловые
границы зерен, двумерные и трехмерные дефекты
- основы современных методов исследования и контроля
дефектов в кристаллах
Цель данного раздела
Слайд 3Классификация дефектов по их размерности
Классификацию дефектов решетки удобно проводить по чисто
геометрическому
признаку - по числу измерений, в которых
нарушения совершенного строения кристалла простираются
на макроскопические расстояния.
нарушения совершенного строения кристалла простираются
на макроскопические расстояния.
Слайд 4Линейные дефекты: дислокации
Лат. dislocatio - смещение, перемещение
«В летнее время, под тенью
акации,
Приятно мечтать о дизлокации»
Козьма Прутков, «Военные афоризмы»
Приятно мечтать о дизлокации»
Козьма Прутков, «Военные афоризмы»
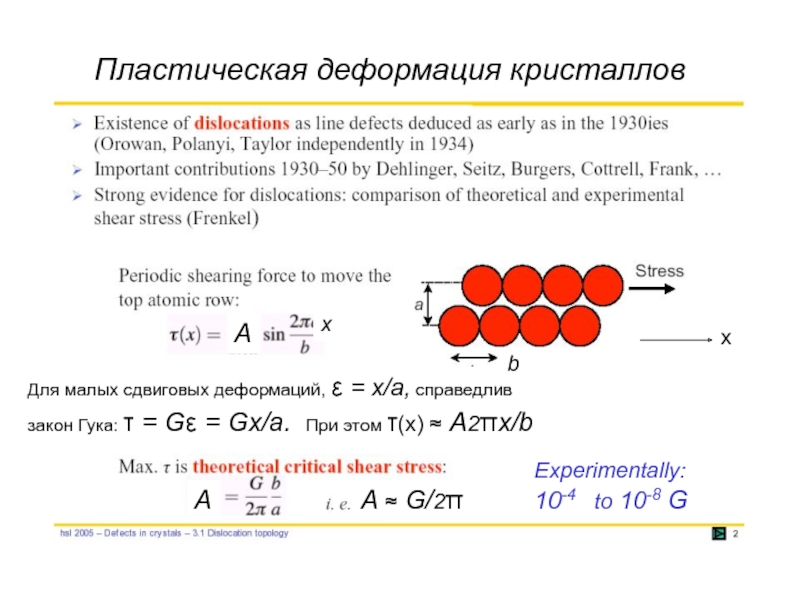
Слайд 5Пластическая деформация кристаллов
A
x
Для малых сдвиговых деформаций, ε = x/a, справедлив
закон
Гука: τ = Gε = Gx/a. При этом τ(x) ≈ A2πx/b
A
A ≈ G/2π
x
b
Experimentally:
10-4 to 10-8 G
Слайд 7Типы дислокаций:
Краевые дислокации - Edge Dislocation:
A portion of an extra plane of atoms
Винтовые дислокации - Screw Dislocation:
Helical atomic displacement around a
line extending through the crystal
Смешанные дислокации - Mixed Dislocation:
Some edge, some screw nature
Винтовые дислокации - Screw Dislocation:
Helical atomic displacement around a
line extending through the crystal
Смешанные дислокации - Mixed Dislocation:
Some edge, some screw nature
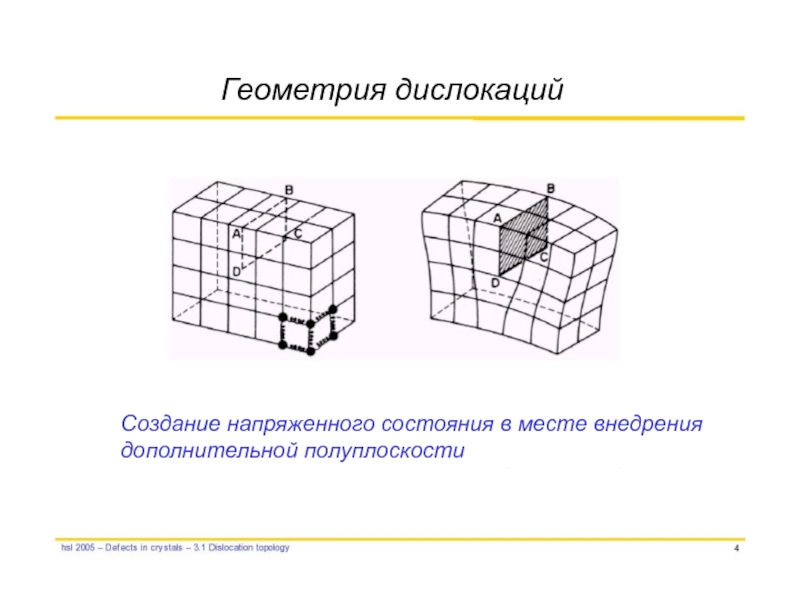
Слайд 8Геометрия дислокаций
Создание напряженного состояния в месте внедрения
дополнительной полуплоскости
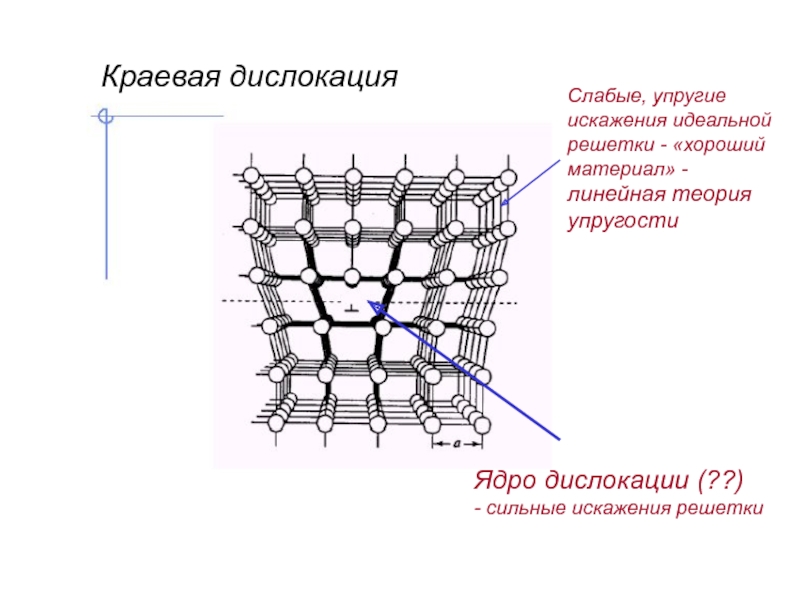
Слайд 9Ядро дислокации (??)
- сильные искажения решетки
Краевая дислокация
Слабые, упругие
искажения идеальной
решетки -
«хороший
материал» -
линейная теория
упругости
материал» -
линейная теория
упругости
Слайд 11Определение дислокации: Дислокацией называется линейный дефект решетки, для которого контур Бюргерса имеет
отличную от нуля невязку.
Слайд 15(a) Perfect simple-cubic crystal.
(b) Displacement of two half-crystals along cut
plane A by lattice vector b results in two surface steps but does not alter the atomic structure inside the crystal.
(c) The same “cut-and-slip” procedure limited to a part of cut plane A introduces an edge dislocation ⊥.
(c) The same “cut-and-slip” procedure limited to a part of cut plane A introduces an edge dislocation ⊥.
Получение дислокации сдвигом в плоскости скольжения
Слайд 16Смешанная дислокация
Сдвиг в плоскости скольжения
По определению вектор
Бюргерса b инвариантен
вдоль дислокации,
хотя
дислокация непрерывно
меняется от винтовой
до краевой
дислокация непрерывно
меняется от винтовой
до краевой
Слайд 19Oscar Rodríguez de la Fuente, Ph.D. Thesis, UCM
Screw dislocation
Edge dislocation
Dislocations
Слайд 22К определению вектора Бюргерса (1)
Перемена направления
вектора ξ на
противоположное
одновременно меняет
направление
вектора
Бюргерса b
Бюргерса b
Слайд 25Свойства дислокаций
Дислокационная линия не может закончиться внутри кристалла,
а только
- на его поверхности
- на внутренней границе раздела ( на границах зерен)
- в дислокационном узле
- с образованием дислокационной петли
- на внутренней границе раздела ( на границах зерен)
- в дислокационном узле
- с образованием дислокационной петли
Слайд 38Движение дислокаций является основным механизмом пластической деформации кристаллов исключения: нитевидные кристаллы, углеродные
нанотрубки
Слайд 39Dislocations make slip 1000 times easier, which is why metals deform
easily
Slip of atom planes over each other due to deformation occurs one atom row at a time, analogous to caterpillar motion or moving a pile of bricks one at a time
Slip of atom planes over each other due to deformation occurs one atom row at a time, analogous to caterpillar motion or moving a pile of bricks one at a time
Слайд 41TEM - 1949 (!)
transmission electron microscopy
“ Изобретение “ дислокаций
(a) TEM
picture of dislocation
structure in single crystal BCC
molybdenum deformed at
temperature 278K.
(b) Dislocations formed bundles
(braids) in single crystal copper
deformed at 77K.
structure in single crystal BCC
molybdenum deformed at
temperature 278K.
(b) Dislocations formed bundles
(braids) in single crystal copper
deformed at 77K.
Слайд 48Three common crystal structures in metals:
Face centered cubic (fcc): ABCABC… packing:
Ni, Cu, Ag, Al, Au
Hexagonal close packed (hcp): ABABAB … packing: Mg, Zn, Co, Ti
Body centered cubic (bcc): Fe, Cr, W, Ta, Mo
Easy for close packed planes to slide over each other: slip planes (plays an important role in determining deformation & strength)
Hexagonal close packed (hcp): ABABAB … packing: Mg, Zn, Co, Ti
Body centered cubic (bcc): Fe, Cr, W, Ta, Mo
Easy for close packed planes to slide over each other: slip planes (plays an important role in determining deformation & strength)
Плоскости скольжения в кристаллах
shear
Слайд 49Совершенные кристаллы (?)
A silicon ingot is a single crystal of Si.
Within the bulk of the crystal, the atoms are arranged on a well-defined periodical lattice. The crystal structure is that of diamond.
Плотность дислокаций
≈ 10 2 см-2
Typical numbers in well annealed metals 106 to 108 cm-2,
in semiconductors 10 to 105 cm -2.
After plastic deformation 1012 cm -2 and above
Слайд 50ρ -1/2
Плотность дислокаций
Определение плотности дислокаций
Выражается в единицах, см-2
Типичные значения в отожженных
металлах
В полупроводниках
После пластической деформации
и выше
ρ = L/ V = Nl/ V = Nl/ lS = N/ S
ρ = L/ V
ρ-1 = S/ N
ρ-1/2 = < r >- среднее расстояние
между дислокациями
