- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы теории подобия презентация
Содержание
- 1. Основы теории подобия
- 2. Определение коэффициентов: теплопроводности λ; лучеиспускание (передача теплоты
- 3. Для определения коэффициентов теплоотдачи αк и массоотдачи
- 4. Два физических процесса считаются подобными, если они
- 5. Простейшим случаем подобия двух объектов является геометрическое
- 6. Каждая величина, характеризующая подобные объекты (или явления),
- 7. Для сходственных (т.е. одинаково расположенных) частиц подобных
- 8. Вместо констант подобия подставим характеризуемые ими величины.
- 9. Критерия подобия устанавливаются из уравнений, описывающих подобные
- 10. Для обоих случаев справедливы уравнения теплопроводности через
- 11. Произведем анализ размерностей Отбросим знаки дифференцирования
- 12. В критерии Нуссельта под l подразумевается любой
- 13. Число Рейнольдса где ω – скорость потока
- 14. Число Грасгофа где
- 15. Число Нуссельта где α – коэффициент конвективной
- 16. Число Прандтля где ср – теплоемкость жидкости
- 17. Критерии, составленные из величин, определяющий характер процесса,
- 18. Критерий Био (Bi) применяется обычно при исследовании
- 19. Физический процесс полностью описывается некоторой системой дифференциальных
- 20. Для того чтобы выяснить, какие из входящих
- 21. Величины, входящие в условие однозначности, задаются внешним
- 22. В основе теории подобия лежат следующие три
- 23. 2-ая теорема. Определяющие и неопределяющие критерии подобных
- 24. 3-я теорема. Для того, чтобы два процесса
- 25. Это особенно выгодно в тех случаях, когда
- 26. Например, критериальное уравнение для теплоотдачи внутри круглых
- 27. Третья теорема устанавливает условия подобия: 1) подобие
Слайд 2Определение коэффициентов:
теплопроводности λ;
лучеиспускание (передача теплоты излучением) αиз;
коэффициента молекулярной диффузии D;
не представляет
Определение коэффициентов теплоотдачи αк и массоотдачи β является трудной задачей.
Эти коэффициенты зависят от множества трудно учитываемых факторов: от режима движения жидкости; от свойств жидкости; от состояния поверхности; от геометрической формы поверхности и т. п.
Слайд 3Для определения коэффициентов теплоотдачи αк и массоотдачи β приходится прибегать к
Система понятий и законов, обосновывающих возможность переноса результатов экспериментов с одного объекта (модели) на другой (реальный), называется теорией подобия.
В основе теории подобия лежат следующие понятия и положения.
Слайд 4Два физических процесса считаются подобными, если они подчиняются одним и тем
Константами подобия – отношение однородных физических величин в сходственных точках модели и натурного объекта.
Слайд 5Простейшим случаем подобия двух объектов является геометрическое подобие.
Два треугольника подобны, если
Величина Cl называется константой геометрического подобия.
Слайд 6Каждая величина, характеризующая подобные объекты (или явления), имеет свою константу подобия.
Для
Для сложных физических процессов, характеризуемых многими величинами, взаимно влияющими друг на друга, значения констант подобия произвольно выбрать нельзя.
Установим условие, ограничивающие выбор констант подобия С.
Рассмотрим движение жидкости со скоростью ω на пути l за время τ:
Слайд 7Для сходственных (т.е. одинаково расположенных) частиц подобных потоков
Введем константы подобия:
Это и
и
или
Слайд 8Вместо констант подобия подставим характеризуемые ими величины.
idem обозначает «одно и тоже»
Записанное соотношение безразмерно и в общем случае отлично от единицы. Данное соотношение называется критерием подобия.
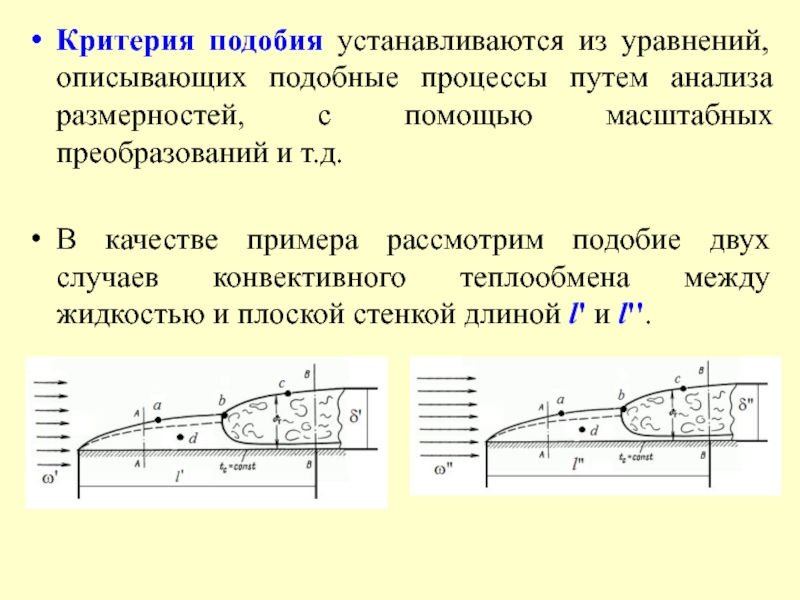
Слайд 9Критерия подобия устанавливаются из уравнений, описывающих подобные процессы путем анализа размерностей,
В качестве примера рассмотрим подобие двух случаев конвективного теплообмена между жидкостью и плоской стенкой длиной l' и l''.
Слайд 10Для обоих случаев справедливы уравнения теплопроводности через пограничный слой δ' и
и конвекции в движущейся массе жидкости (закон Ньютона)
где λ и α – средние значения коэффициентов теплопроводности и теплоотдачи.
При стационарном режиме
Слайд 11Произведем анализ размерностей
Отбросим знаки дифференцирования и пологая характерным размером x =
Полученный безразмерный комплекс называется числом Нуссельта
– дифференциальное уравнение одномерной, стационарной конвективной теплоотдачи между жидкостью и стенкой
откуда
Слайд 12В критерии Нуссельта под l подразумевается любой линейный параметр, однозначно определяющий
Величины λ и α берутся однозначно, т.е. или в обоих случаях средние, или отнесенные к каким-то сходственным точкам.
Основные критерии подобия, применяющиеся при решении задач теплообмена, и их физический смысл.
Аналогичные критерии с соответствующей заменой коэффициентов и потенциалов применяются при решении задач массоотдачи.
Слайд 13Число Рейнольдса
где ω – скорость потока (м/с); d – эквивалентный диаметр
Критерий Рейнольдса характеризует гидродинамический режим движения, являясь мерой отношения сил инерции и вязкости. При малых силах инерции и больших силах вязкости движение ламинарное, в противоположном случае - турбулентное.
Слайд 14Число Грасгофа
где
– для идеального газа; Δt – разность температур в двух точках системы потока и стенки (К). Если ρж и ρс – плотности жидкости в двух точках системы, то
Критерий Грасгофа характеризует гидродинамическое подобие при свободном движении жидкости. Отражает соотношение между подъемной силой, заставляющей всплывать нагретые частицы теплоносителя (архимедова сила), и силой вязкостного трения, препятствующей подъему этих частиц. Чем Gr выше, тем свободное движение интенсивнее.
Слайд 15Число Нуссельта
где α – коэффициент конвективной теплоотдачи (Вт/м2·К).
Критерий Нуссельта характеризует отношение
Чем Nu выше, тем интенсивнее процесс конвективного теплообмена.
Слайд 16Число Прандтля
где ср – теплоемкость жидкости при постоянном давлении (Дж/кг·К);
λ –
a – коэффициент температуропроводности (м2/с).
Критерий Прандтля характеризует физические свойства жидкости и способность распространения тепла в жидкости.
Для газов Pr = 0,67÷1,0 и зависит только от атомности;
для жидкостей Pr = 1,0÷2500.
Слайд 17Критерии, составленные из величин, определяющий характер процесса, но не включающие искомых
Определяющими называются величины, заданные в условиях однозначности физических процессов, являющиеся независимыми переменными.
Например, при расчете конвективного теплообмена критерий Нуссельта Nu является неопределяющим, поскольку в него входит искомая величина α (коэффициент теплоотдачи). Критерии Рейнольдса Re и Прандтля Pr в этих расчетах определяющие.
Слайд 18Критерий Био (Bi) применяется обычно при исследовании нестационарного процесса распространения теплоты
По условию задачи бывают известны также характерный размер l и коэффициент теплопроводности λ.
Поэтому критерий Био является также определяющим.
Температура, при которой определяются физические параметры λ, а, ν и др., входящие в критерии подобия называется определяющей температурой, а характерный размер теплоносителя или канала δ, l, d – определяющим размером.
Слайд 19Физический процесс полностью описывается некоторой системой дифференциальных уравнений и присоединенных к
В таком случае принципиально возможно получить решение относительно любого из этих неизвестных, т.е. выразить интеграл рассматриваемой системы уравнений в виде некоторой функции
где yi – искомая неизвестная (зависимая) переменная величина;
xi – независимые переменные, входящие в основную систему уравнений.
(4)
Слайд 20Для того чтобы выяснить, какие из входящих в уравнение переменных являются
геометрические условия (форма и размер тела, координатная система);
физические условия (физические свойства среды и тела);
временные условия, характеризующие состояние системы в начальный момент времени;
граничные условия, которые определяют условия взаимодействия системы с окружающей средой.
Слайд 21Величины, входящие в условие однозначности, задаются внешним образом по отношению к
Все остальные переменные, входящие в основные уравнения, являются зависимыми переменными.
Величины xi в формуле (4) составлены из условий однозначности.
Слайд 22В основе теории подобия лежат следующие
три теоремы подобия
1-ая теорема. В сходственных
Слайд 232-ая теорема. Определяющие и неопределяющие критерии подобных процессов связаны между собой
Обозначим через Kо определяющие критерии, а через Kн – неопределяющие, то критериальное уравнение в общей форме будет иметь вид:
(5)
Слайд 243-я теорема. Для того, чтобы два процесса были подобны, необходимо и
Поясним содержание 2-ой и 3-ей теорем.
Вторая теорема является для практических целей самой плодотворной.
Смысл второй теоремы сводится к тому, что можно, не интегрируя дифференциальные уравнения исследуемых подобных процессов, получать расчетные формулы, заменяя эти дифференциальные уравнения критериальными.
Слайд 25Это особенно выгодно в тех случаях, когда дифференциальное уравнение не интегрируется.
Тогда
Количество переменных при этом сокращается, что облегчает исследование.
Затем между критериями экспериментально устанавливается функциональная зависимость – критериальное уравнение. Эти уравнения получаются для строго определенных условий, поэтому пользоваться ими можно лишь в том диапазоне изменения определяющих критериев, который имел место в опытах, т.е. в пределах, ограниченных условиями подобия.
Слайд 26Например, критериальное уравнение для теплоотдачи внутри круглых труб при условиях, близких
Это уравнение применимо при
и
Определяющим размером в числах Рейнольдса Re и Нуссельта Nu является внутренний диаметр трубы, определяющей температурой – температура потока t1 теплоносителя. В случае, если температура потока t1 и стенки tст заметно отличаются друг от друга, величину критерия Nu полученную из формулы (6), надо умножить на специальную поправку.
(6)
Слайд 27Третья теорема устанавливает условия подобия:
1) подобие условий однозначности;
2) равенство определяющих критериев
Если определяющие критерии одинаковы, то критерии, составленные из величин, не относящихся к условиям однозначности, т.е. неопределяющие, тоже будут равны.
Теория подобия широко используется при моделировании самых различных процессов и явлений, особенно при рассмотрении конвективного теплообмена и определения для разных его случаев коэффициента теплоотдачи.