- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Физические основы получения информации презентация
Содержание
- 1. Физические основы получения информации
- 2. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ. ЭЛЕКТРИЧЕСКИЕ И МАГНИТНЫЕ СВОЙСТВА
- 3. Электрическое поле. Характеристики материалов в электрическом поле
- 4. Электрические заряды в электрическом поле Основной характеристикой
- 5. Единицей измерения напряженности электрического поля является вольт
- 6. Единицей измерения разности электрических потенциалов (электрического напряжения)
- 7. Основными электрическими свойствами материалов физических объектов, проявляющимися
- 8. Величина, обратная удельной электрической проводимости: ρ
- 9. Сопротивление металлов электрическому току связано с процессом
- 10. В проводниках не может существовать статического электрического
- 11. Если в вакууме сила взаимодействия зарядов по
- 12. Проводники обладают электропроводностью, диэлектрики - поляризуемостью, вещества
- 13. Магнитное поле. Характеристики материалов в магнитном поле
- 14. Единица измерения магнитной индукции - тесла (Тл).
- 15. Важное значение в теории электромагнетизма имеет величина
- 16. Задача Определить разность потенциалов между точками 1
- 17. В однородном электрическом поле где
- 18. Определить точку кривой первоначального намагничивания B(H), для
- 19. Геометрический смысл нормальной магнитной проницаемости в некоторой
- 21. Задача 3 Определить мгновенное значение ЭДС e
- 22. Согласно закону электромагнитной индукции ЭДС, наводимая в
- 23. Решение Дифференцированием величины Φ по времени получаем:
- 24. ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАНИЯ В ЭЛЕКТРИЧЕСКИХ ПОЛЯХ Эти измерительные
- 25. Электроемкостное измерительное преобразование Электроемкостное измери- тельное преобразование
- 28. Физический смысл емкости Предположим, что заряд емкости
- 29. Добротность конденсатора Q: Угол потерь δ
- 30. Энергия электростатического поля конденсатора. Силы, развиваемые в
- 31. Энергия электростатического поля конденсатора. Силы, развиваемые в
- 32. Электропотенциальное измерительное преобразование Электропотенциальное измерительное преобразование основано
- 33. Зависимость разности потенциалов между двумя точками 1
- 34. Данный вариант электропотенциального измерительного преобразования нашел
- 35. Пьезоэлектрическое измерительное преобразование Пьезоэлектрическое измерительное преобразование основано
- 36. Пьезоэффект является обратимым физическим явлением. Обратный
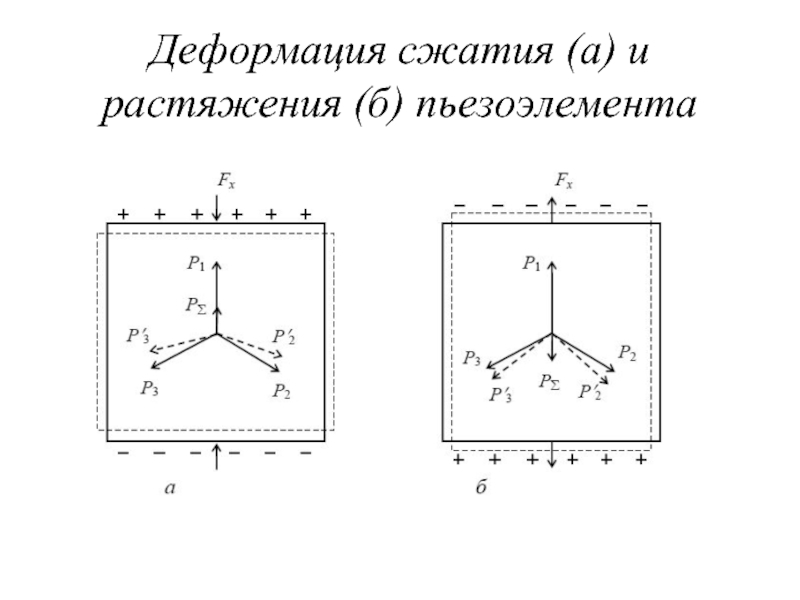
- 37. Деформация сжатия (а) и растяжения (б) пьезоэлемента
- 38. Наличие при деформации обусловливает возникновение на
- 39. Тензорезистивное измерительное преобразование Основано на использовании тензоэффекта,
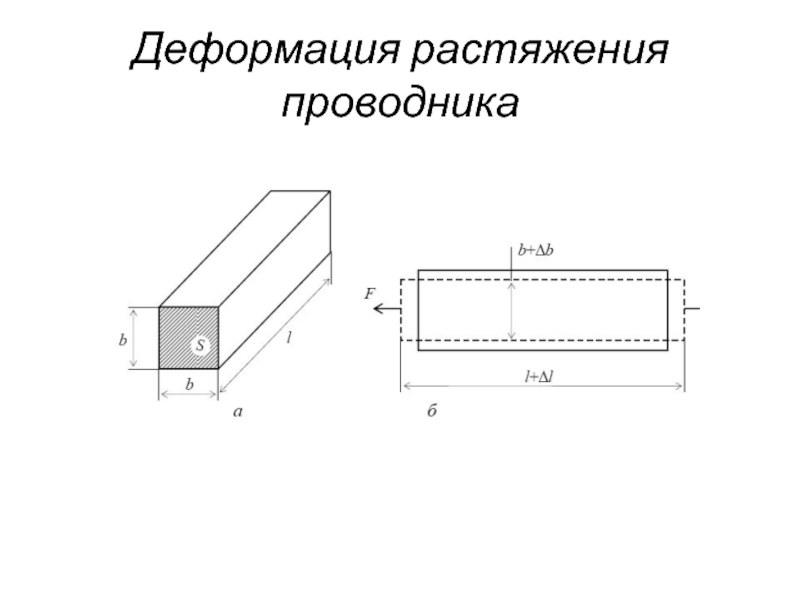
- 40. Деформация растяжения проводника
- 41. Электрическое сопротивление стержня длиной l, с площадью
- 42. Для стержня квадратного сечения:
- 44. Электрохимическое измерительное преобразование Основано на физико-химических процессах,
- 45. Электропроводность растворов Высокой электрической проводимостью обладают водные
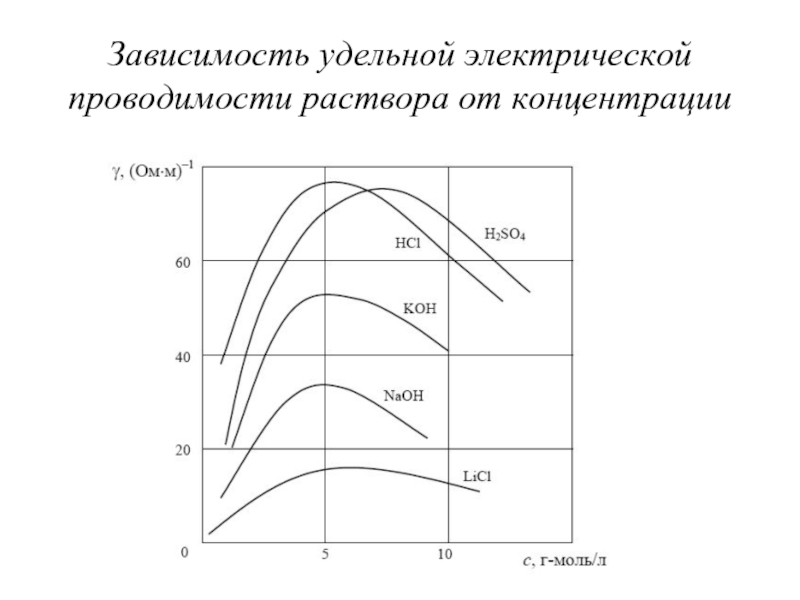
- 46. Зависимость удельной электрической проводимости раствора от концентрации
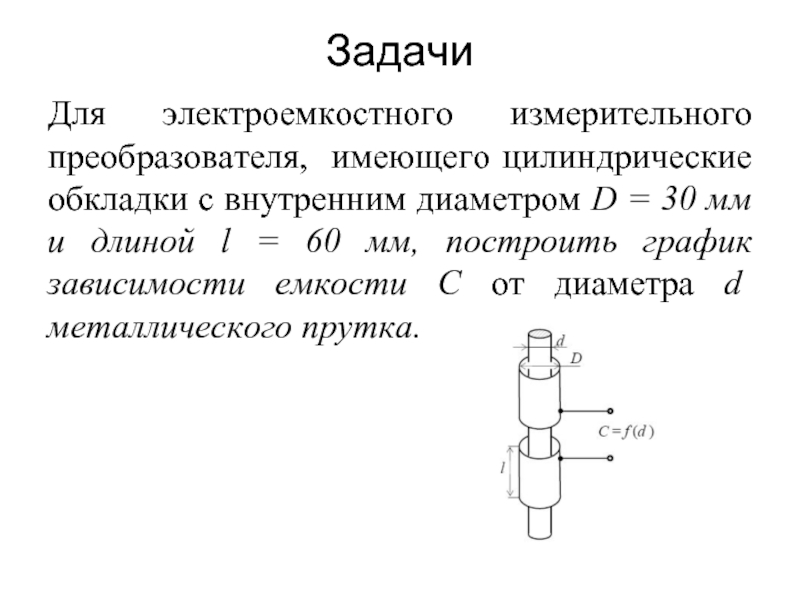
- 47. Задачи Для электроемкостного измерительного преобразователя, имеющего цилиндрические
- 48. Решение Рассматриваемый электроемкостной преобразователь представляет собой два
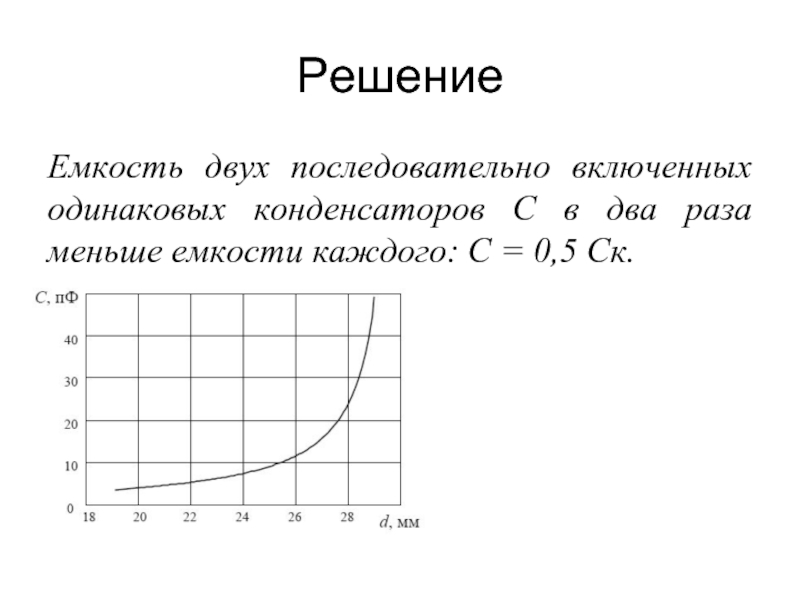
- 49. Решение Емкость двух последовательно включенных одинаковых конденсаторов
- 50. Задача Определить разность потенциалов Δϕ между электродами
- 51. Решение Зависимость разности потенциалов между электродами при
- 52. Решение Зависимость S(x) площади поперечного сечения от
- 53. Решение С учетом этого получаем искомое выражение для разности потенциалов:
- 54. Решение Подстановкой заданных условием задачи значений величин
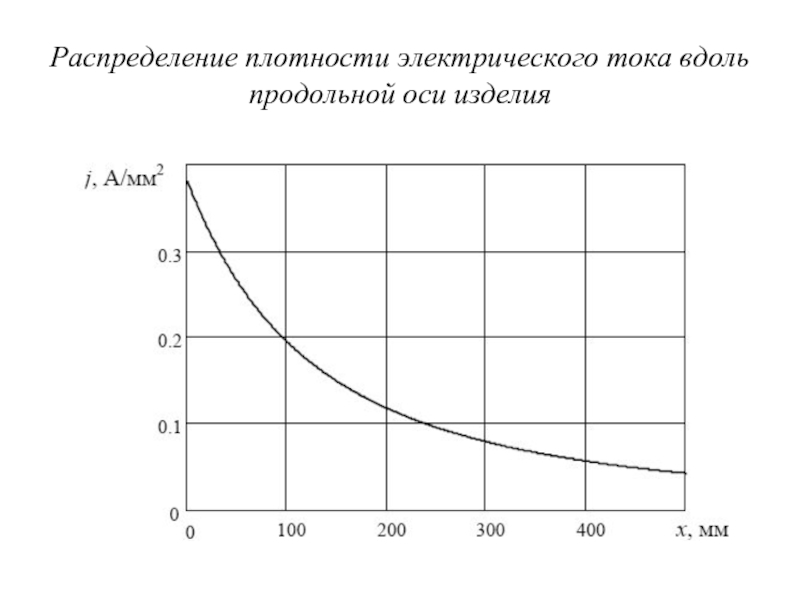
- 55. Распределение плотности электрического тока вдоль продольной оси изделия
- 56. Задача Определить абсолютное и относительное изменения электрического
- 57. Решение Площадь поперечного сечения проводника:
- 58. Значение напряжения не превышает предела упругости материала,
Слайд 2
ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ. ЭЛЕКТРИЧЕСКИЕ И МАГНИТНЫЕ СВОЙСТВА МАТЕРИАЛОВ
Электромагнитное поле − форма существования
Между частицами и их полем точной границы нет.
Однако электрический заряд имеет лишь частица материи, сосредоточенная в весьма малой области пространства, а вне этой области материя существует в виде электромагнитного поля и объемная плотность заряда равна нулю.
Слайд 3Электрическое поле. Характеристики материалов в электрическом поле
Электрическое поле − электромагнитное поле,
Слайд 4Электрические заряды в электрическом поле
Основной характеристикой электрического поля является вектор напряженности
Слайд 5Единицей измерения напряженности электрического поля является вольт на метр (В/м). Энергетической
где А − работа по перемещению положительного заряда q из точки 1 в точку 2.
Слайд 6Единицей измерения разности электрических потенциалов (электрического напряжения) является вольт (В). Поскольку
и напряженности электрического поля.
Слайд 7Основными электрическими свойствами материалов физических объектов, проявляющимися при взаимодействии объектов с
По электрическим свойствам вещества разделяют на проводники и изоляторы.
Плотность электрического тока j в проводнике прямо пропорциональна напряженности электрического поля (закон Ома):
j = σE,
где σ − удельная электрическая проводимость
Слайд 8Величина, обратная удельной электрической проводимости:
ρ = 1/σ,
называется удельным электрическим сопротивлением.
Удельное электрическое сопротивление металлов и сплавов составляет
0,015…1,3 мкОм⋅м
Слайд 9Сопротивление металлов электрическому току связано с процессом рассеяния проводимости электронов в
Другим фактором, влияющим на сопротивление, является концентрация в материале свободных электронов, определяемая количеством свободных уровней энергии зонной диаграммы. Последнее объясняет тот факт, что одновалентные металлы (медь, серебро, золото, щелочные металлы) имеют наиболее высокую электропроводность
Слайд 10В проводниках не может существовать статического электрического поля, поскольку приложенное электрическое
материалы, обладающие свойством ослаблять взаимодействие зарядов по сравнению с вакуумом, которые получили название диэлектриков.
Слайд 11Если в вакууме сила взаимодействия зарядов по модулю равна:
в диэлектрике ее
ε0 -электрическая постоянная
εr − относительная диэлектрическая проницаемость, основная электрическая характеристика диэлектриков
Слайд 12Проводники обладают электропроводностью, диэлектрики - поляризуемостью, вещества при воздействии на которые
Слайд 13Магнитное поле. Характеристики материалов в магнитном поле
Магнитное поле − электромагнитное поле,
Основной характеристикой магнитного поля является вектор магнитной индукции B, который может быть определен по силе F , с которой поле действует на заряд q, перемещающийся со скоростью V
Слайд 14Единица измерения магнитной индукции - тесла (Тл). Способность электрического тока возбуждать
Единица измерения магнитного момента является ампер-
квадратный метр (А⋅м2).
Слайд 15Важное значение в теории электромагнетизма имеет величина Ф, называемая магнитным потоком.
Единицей
Слайд 16Задача
Определить разность потенциалов между точками 1 и 2 в однородном электрическом
точки силовыми линиями a = 3 см
Слайд 17В однородном электрическом поле
где α – угол между прямой, соединяющей точки,
Отсюда
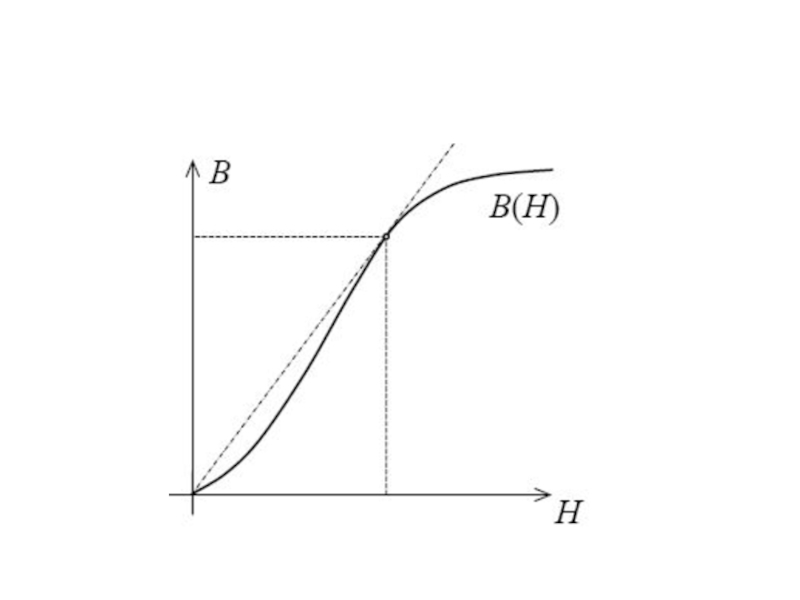
Слайд 18Определить точку кривой первоначального намагничивания B(H), для которой имеет место равенство
Решение
Относительные нормальная и дифференциальная магнитные проницаемости связаны с величинами магнитной индукции В и напряженности магнитного поля Н следующим образом:
Слайд 19Геометрический смысл нормальной магнитной проницаемости в некоторой точке кривой намагничивания заключается
точку с началом координат, а геометрический смысл дифференциальной
магнитной проницаемости заключается в равенстве ее значения тангенсу угла наклона касательной в рассматриваемой точке кривой намагничивания. Отсюда вытекает, что при равенстве значений относительно нормальной и дифференциальной магнитной проницаемости μr и μd должно иметь место совпадение прямой, соединяющей точку кривой намагничивания с началом координат, и касательной к кривой намагничивания.
Данному условию помимо точки, совпадающей с началом координат, удовлетворяет точка кривой первоначального намагничивания, которой
соответствует максимальное значение угла наклона прямой, соединяю-
щей эту точку с началом координат, и, соответственно, максимальное
значение относительной нормальной магнитной проницаемости.
Слайд 21Задача 3
Определить мгновенное значение ЭДС e в момент времени t =
составляют с плоскостью контура угол β = 30°, а индукция изменяется во времени по закону
Слайд 22Согласно закону электромагнитной индукции ЭДС, наводимая в контуре,
Магнитный поток Φ индукции
Слайд 24ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАНИЯ
В ЭЛЕКТРИЧЕСКИХ ПОЛЯХ
Эти измерительные преобразования основаны на физических эффектах, результатом
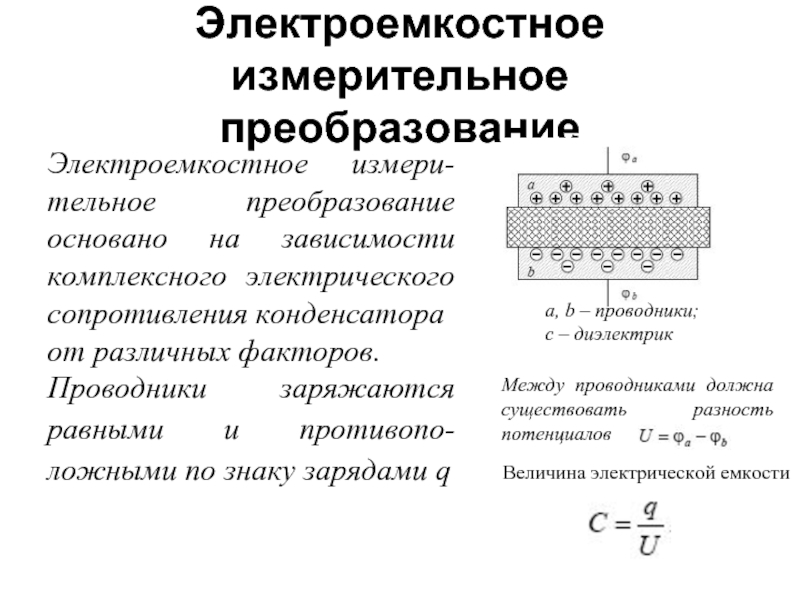
Слайд 25Электроемкостное измерительное преобразование
Электроемкостное измери- тельное преобразование основано на зависимости комплексного электрического
от различных факторов.
Проводники заряжаются равными и противопо-ложными по знаку зарядами q
a, b – проводники;
с – диэлектрик
Между проводниками должна существовать разность потенциалов
Величина электрической емкости
Слайд 28Физический смысл емкости
Предположим, что заряд емкости осуществляется от источника постоянного фиксированного
U=q/C.
Чем больше емкость конденсатора, тем меньшая работа требуется для заряда конденсатора до фиксированного значения.
Слайд 29Добротность конденсатора Q:
Угол потерь δ (обычно вместо угла рассматривается tgδ)
ω –
Значение угла потерь зависит также от действия на диэлектрик внешних факторов: температуры и влажности окружающей среды, частоты и амплитуды подаваемого напряжения, интенсивности воздействия ионизирующими излучениями. Благодаря этому существует возможность путем измерения угла потерь получать измерительную информацию о перечисленных выше параметрах.
Слайд 30Энергия электростатического поля конденсатора.
Силы, развиваемые в электростатическом поле
Емкостной преобразователь является обратимым
При перемещении обкладок на малые значения dx или dα силами электростатического взаимодействия совершается элементарная механическая работа dA, которая определяется в зависимости от вида взаимного перемещения по одной из формул:
Слайд 31Энергия электростатического поля конденсатора.
Силы, развиваемые в электростатическом поле
Работа совершается за счет
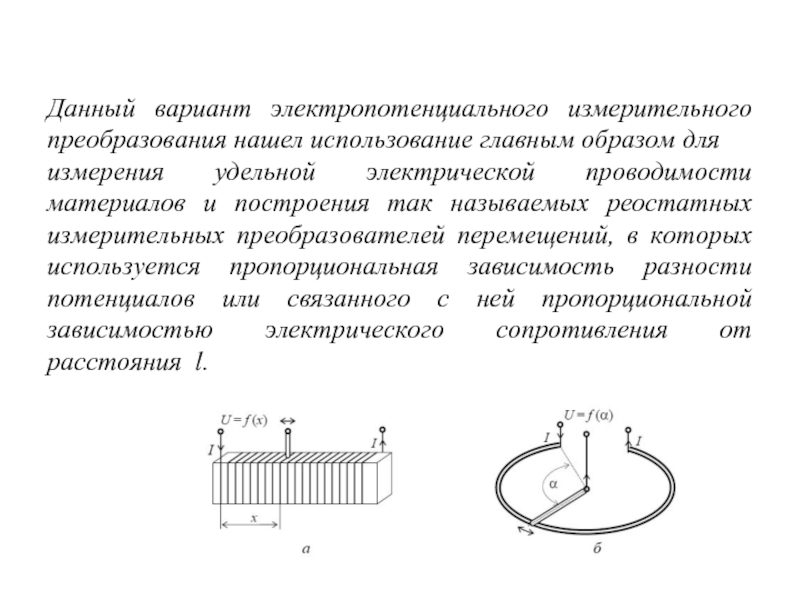
Слайд 32Электропотенциальное измерительное преобразование
Электропотенциальное измерительное преобразование основано на зависимости распределения электрического потенциала
Слайд 33Зависимость разности потенциалов между двумя точками 1 и 2 на поверхности
σ - удельная электрическая проводимость материала проводника
Слайд 34
Данный вариант электропотенциального измерительного преобразования нашел использование главным образом для
измерения удельной
Слайд 35Пьезоэлектрическое измерительное преобразование
Пьезоэлектрическое измерительное преобразование основано на использовании прямого и обратного
Слайд 36
Пьезоэффект является обратимым физическим явлением. Обратный пьезоэффект заключается в возникновении в
В недеформированном состоянии пьезоэлемент в целом, как и составляющие его отдельные элементарные ячейки, является электрически нейтральным. Электрические поля всех его зарядов уравновешивают друг друга, проявлением чего является отсутствие зарядов на электродах пьезоэлемента.
Если к пьезоэлементу приложить механическое усилие в направлении оси x, то в результате деформации элементарных ячеек их нейтральность нарушается.
Слайд 38
Наличие при деформации обусловливает возникновение на электродах пьезоэлемента поляризационных зарядов, имеющих
d – пьезоэлектрический модуль
Слайд 39Тензорезистивное измерительное преобразование
Основано на использовании тензоэффекта, заключающегося в изменении активного электрического
Слайд 41Электрическое сопротивление стержня длиной l, с площадью поперечного сечения S и
материала ρ определяется выражением:
Изменение сопротивления в результате деформации
Слайд 42
Для стержня квадратного сечения:
В диапазоне упругих деформаций изменение поперечного размера стержня
μ − коэффициент Пуассона, связывающий продольные и поперечные деформации.
Слайд 44Электрохимическое измерительное преобразование
Основано на физико-химических процессах, протекающих в проводящих электрический ток
Электрохимический преобразователь представляет собой электролитическую ячейку, заполненную проводящим электрический ток раствором и имеющую два или более электродов. В общем случае электроды непосредственно участвуют в физико-химических процессах, протекающих в ячейке.
Слайд 45Электропроводность растворов
Высокой электрической проводимостью обладают водные растворы солей, кислот и оснований.
Являясь веществом с высокой диэлектрической проницаемостью вода, поляризуясь в электрическом поле ионов растворенного вводе вещества, ослабляет силы электрического взаимодействия между этими ионами. Последнее приводит к интенсивной диссоциации молекул растворенного вещества на свободные ионы (носители за-
рядов). Вещества, растворяющиеся в воде с образованием положительных и отрицательных свободных ионов, называются электролитами.
Удельная электрическая проводимость раствора γ зависит от его
концентрации и пропорциональна химической активности раствора:
f − коэффициент активности; с − молярная концентрация раствора; a − химическая активность раствора; λ − эквивалентная электропроводность, соответствующая единичному значению химической активности раствора.
Слайд 47Задачи
Для электроемкостного измерительного преобразователя, имеющего цилиндрические обкладки с внутренним диаметром D
Слайд 48Решение
Рассматриваемый электроемкостной преобразователь представляет собой два последовательно соединенных одинаковых конденсатора. Одной
Слайд 49Решение
Емкость двух последовательно включенных одинаковых конденсаторов С в два раза меньше
Слайд 50Задача
Определить разность потенциалов Δϕ между электродами электропотенциального измерительного преобразователя, установленного на
значение постоянного электрического тока, пропускаемого через изделие в продольном
направлении I = 30 А, расстояние между электродами l = 20 мм, а расстояние от вершины конуса до ближайшего электрода b = 200 мм. Построить график изменения плотности электрического тока вдоль продольной оси изделия, принимая его одинаковым по площади поперечного сечения.
Слайд 51Решение
Зависимость разности потенциалов между электродами при протекании постоянного электрического тока вдоль
от параметров проводника может быть найдена с учетом непостоянства площади поперечного сечения провод ника вдоль продольной оси ox:
Слайд 52Решение
Зависимость S(x) площади поперечного сечения от координаты x (начало координат совпадает
поперечного сечения от координаты x:
Слайд 54Решение
Подстановкой заданных условием задачи значений величин получаем:
С учетом ранее полученных соотношений
Слайд 56Задача
Определить абсолютное и относительное изменения электрического сопротивления проводника длиной l =
Слайд 57Решение
Площадь поперечного сечения проводника:
Сопротивление проводника в недеформи-рованном состоянии
Механическое продольное напряжение, обусловленное
Слайд 58Значение напряжения не превышает предела упругости материала, и следовательно деформация носит
Значения абсолютного и относительного изменений электрического сопротивления находятся