Основы автоматического управления. Введение. Основные понятия и определения презентация

бюджетное образовательное учреждение
высшего профессионального образования
БАЛТИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ВОЕНМЕХ» им. Д.Ф. УСТИНОВА

Основы автоматического управления

Кафедра Н1 Мехатроника и робототехника

К.т.н., доцент Савельев Б.Н.

Санкт – Петербург 2015 г.

Часть первая

ПОЛЗУНОВА

РЕГУЛЯТОР УАТТА

Рис. 5

момента и компенсации противо ЭДС

Х1 и Х2 и одной выходной величиной Y, динамическое уравнение которого имеет вид нелинейного дифференциального уравнения:

Будам считать, что динамический процесс в системе протекает в окрестности некоторой точки установившегося статического режима, в которой переменные звена имеют постоянные значения Эту точку называют точкой линеаризации.

Уравнение звена в этом режиме:

а переменные в динамическом режиме можно представить:

и т.д.

При линеаризации производные рассматриваются как самостоятельные переменные.

Пути линеаризации

1. Если близка к линейной в окрестности точки линеаризации, то ее можно просто заменить линейной зависимостью, и ограничить диапазон изменения воздействий.

2. Если не линейна в окрестности точки линеаризации, но непрерывно дифференцируема, ее можно разложить в ряд Тейлора в этой точке.

3. Если существенно не линейна, т.е. не является непрерывно дифференцируемой, а содержит разрывы, неоднозначности и т.п. используют гармоническую линеаризацию, т.е. при эквивалентном гармоническом воздействии выходную переменную раскладывают в ряд Фурье. Из него и определяют коэффициенты линеаризации.

(1)

(2)

второй путь. Рассмотрим его подробнее

(члены высшего порядка малости)

(3)

- значение частной производной при подстановке в нее значений переменных и их производных в точке линеаризации.

Пренебрегая членами высшего порядка малости и вычитая из уравнения (3) уравнение установившегося режима (2),получим линеаризованное дифференциальное уравнение звена в отклонениях или в вариациях:

(4)

- Линеаризованное уравнение звена является приближенным, т.к. не учитывает малые высшего порядка.

- Переменными в уравнении являются отклонения от значений в точке линеаризации.

- Уравнение справедливо при малых отклонениях от значений в точке линеаризации.

Комментарий:

полиномов имеют размерность времени в степени соответственно, а коэффициенты и - размерность отношения размерностей к и к , поэтому часто вводят обозначения:

т.е. реакция содержит информацию об этих свойствах и может служить их моделью.

Графические формы представления математического описания звеньев и систем

и бесконечно большой амплитуды с площадью равной 1. Дельта функцию обозначают .

Весовая функция представляет собой реакцию звена (изменение во времени выходной переменной) при подачи на его вход единичной импульсной функции (дельта функции).

Легко заметить, что и установить

Действительно, импульс шириной и амплитудой N можно представить в виде двух скачков и

Помножив и поделив на и увеличивая N так, чтобы , в пределе получим:

2.Весовая функция (импульсная переходная характеристика)

Графически и представляются следующим образом:

Весовую функцию будем обозначать

Иными словами при

Тогда реакцию звена можно выразить через переходные характеристики

(24)

По определению передаточная функция звена или системы равна отношению изображений по Лапласу выходной и входной переменных при нулевых начальных условиях, следовательно при подаче на вход звена дельта функции она будет равна отношению изображений по Лапласу весовой функции и дельта функции, т.е.




где: изображение по Лапласу весовой функции ,


изображение по Лапласу дельта функции ,равно 1.

Таким образом весовая функция связана с передаточной функцией звена преобразованием Лапласа.
Используя обратное преобразование, получим:

(25)

(27)

(26)

где изображение по Лапласу переходной функции , получим :

Так как

виды мат. моделей звена, позволяют получить реакцию звена при воздействиях произвольного вида и нулевых начальных условиях, т.е. когда входное воздействие может быть представлено X(t)1(t).
Произвольную функцию времени Х(t)1(t) можно представить в виде суммы ступенчатых воздействий величиной Хк , подаваемых через промежутки времени , или в виде суммы импульсов высотой Xi и длительностью .










Переходный процесс y(t) на выходе звена в этом случае может быть определен как предел суммы реакций звена на ступенчатые воздействия величиной при , или как предел суммы реакций на импульсы величиной и длительностью при .
Пределом суммы при является интеграл, который носит название интеграла Дюамеля-Карсона

Реакция звена или системы при не типовых воздействиях

- угловая частота; Т – период.

- полиномы от Р ( ) степени m и n.

Частотные характеристики звеньев и САР

Основной частотной характеристикой динамических звеньев или САР является их частотная передаточная функция, под которой понимают отношение изображений по Фурье выходной и входной переменных при нулевых начальных условиях и отсутствии других воздействий. Рассмотрим существо этого понятия. Пусть есть звено или САР с одним входом и одним выходом, динамика которого описывается линейным уравнением:

где: X(t) и Y(t) – входное воздействие и выходная переменная звена или САР;
K – коэффициент передачи звена или САР;

Схема такого звена или САР может быть представлена в виде:

Подадим на вход звена гармоническое воздействие:

На выходе звена в установившемся режиме будут вынужденные колебания переменной той же частоты, но другой амплитуды и фазы, т.е.:

где: ym –амплитуда выходной переменной; - сдвиг по фазе относительно Х(t).

Частотная передаточная функция

Такое представление косинуса соответствует изображению его на комплексной плоскости в виде двух векторов вращающихся с частотой в разные стороны.
В линейном звене можно рассматривать прохождение каждой составляющей входного воздействия отдельно, а т. к. они отличаются лишь знаком в показателе степени и соотношения между y(t) и x(t) ,а также y(t) и x(t) одинаковы, будем рассматривать лишь одну и использовать символическую запись

+

+

-

-

Подставляя выражения для x(t), y(t) и их производных в уравнение движения звена, получим:

(32)

Re

Im

(33)

(34)

входного воздействия будут различными модуль, фаза, действительная и мнимая составляющие частотной передаточной функции звена, т.е. они являются функциями частоты. Следовательно они могут быть построены графически.
Зависимость от частоты называют «амплитудно-частотной характеристикой»(АЧХ)
Зависимость от частоты называют «фазовой частотной характеристикой»(ФЧХ)
Зависимость от частоты называют «действительной частотной характеристикой» (ДЧХ)
Зависимость от частоты называют «мнимой частотной характеристикой» (МЧХ)
Примерный вид этих характеристик для инерционных звеньев:

Рис.39 ФЧХ

Рис.40 ДЧХ

Рис. 41 МЧХ

АЧХ показывает, какой коэффициент передачи (усиления) звена будет на каждой частоте, а ФЧХ- каким будет сдвиг фазы.
АЧХ может быть монотонной или иметь максимум. При наличии max звено имеет собственную частоту, которая называется резонансной.
ФЧХ у инерционных звеньев отрицательна, т.к. выходные колебания отстают по фазе от колебаний на входе.

Рис.38 АЧХ

действительную и мнимую составляющие или через модуль и фазу АФЧХ может быть построена с использованием прямоугольной или полярной систем координат. По оси абсцисс откладывают действительную часть , а по оси ординат – мнимую часть частотной передаточной функции, или откладывают угол (фазу ) и модуль

АМПЛИТУДНО-ФАЗОВАЯ ЧАСТОТНАЯ ХАРАКТЕРИСТИКА

Наряду с рассмотренными частотными характеристиками в ТАУ широко используется и объединяющая их характеристика, которая называется амплитудно-фазовой частотной характеристикой (АФЧХ).

АФЧХ строится на комплексной плоскости и представляет годограф вектора частотной передаточной функции при изменении частоты от 0 до

Амплитудно-фазовая частотная характеристика имеет аналитическое выражение в виде частотной передаточной функции

(38)

Частотные характеристики имеют более широкое применение и используются не только для случаев гармонических воздействий.
Если входное воздействие Х(t) периодическая функция времени, то ее можно разложить в ряд Фурье и представить в виде суммы гармоник или, используя формулы Эйлера, в виде суммы сопряженных векторов вращающихся на комплексной плоскости




,

где: Хк – амплитуда; - угловая частота k-ой гармоники; -основная частота, Т – период.
- комплексный модуль сопряженных векторов К-ой гармоники на комплексной
плоскости, содержащий информации о модуле векторов и их начальной фазе.
Если входное воздействие функция произвольного вида Х(t)1(t) (непериодическая), то, используя преобразования Фурье, ее можно представить в виде бесконечной суммы бесконечно малых по величине гармоник или сопряженных векторов вращающихся на комплексной плоскости с различными частотами . Эта сумма выражается обратным преобразованием Фурье



где изображение Х(t) по Фурье.

Это следует из сути преобразований Фурье, как предельного случая разложения периодической функции в ряд при периоде Т и основной частоте
- комплексный модуль вектора К-той гармоники (содержит информацию о
величине и начальной фазе) .
- относительный комплексный модуль К-ой гармоники.

систем прохождение каждой гармонической составляющей входного воздействия можно рассматривать отдельно. Она будет вызывать в выходной переменной составляющую той же частоты, но другой амплитуды и фазы. Сумма составляющих на выходе звена и представляет собой выходную переменную y(t). Для периодического сигнала

т.е. частотная передаточная функция связана с весовой функцией преобразованием Фурье

Для сигнала произвольного вида y(t)1(t),

и фазовую частотные характеристики удобно строить в логарифмических масштабах координат.

Построенные с использованием логарифмических масштабов эти характеристики называются:

Логарифмическая амплитудная частотная характеристика (ЛАЧХ) ;

Логарифмическая фазовая частотная характеристика (ЛФЧХ) .

Ее единицей измерения является децибел, т.е. 0,1 бела. (1бел – десятичный логарифм, соответствующий усилению мощности в 10 раз, 2 бела – в 100 раз и т.д.).

Ось абсцисс проходит через (.) 0дб, что соответствует модулю звена равному1, а ось ординат привязывают к какой – либо частоте, так чтобы ЛАЧХ в основном была справа.

Рис.43

логарифмических частотных характеристик.

-20дб/дек

20дб/дек

-40дб/дек

20дб/дек

уравнения первого порядка при Х(t)=1(t)

1.2.1 Временные характеристики позиционного звена первого порядка.

- переходная характеристика

Звенья этого типа в установившемся статическом режиме дают на выходе сигнал пропорциональный входному воздействию, однако в динамике пропорциональность нарушается из-за инерционных свойств звена.
Звенья этого типа описываются дифференциальными уравнениями вида:

Аналитическим выражением переходной характеристики является решение дифференциального уравнения звена, которое ищется в виде:

По переходной функции h(t), полученной экспериментально, можно определить К и Т звена. При времени t = T

1.2 Позиционное (пропорциональное, статическое, апериодическое) звено первого порядка

(43)

(44)

(45)

(46)

(47)

Аналитическое выражение весовой функции может быть получено из выражения для h(t),т.к.
Для пропорционального звена первого порядка

Рис.46

По весовой функции w(t), полученной экспериментально, тоже можно определить К и Т звена. При времени t = T

Откладывая 0,368К/Т на характеристике , легко получить Т. Величина К определяется как

Теоретически переходный процесс в звене длится бесконечно долго, т.к. , асимптотически. На практике считают, что переходный процесс закончен при . . Найденные значения К и Т позволяют записать передаточную функцию пропорционального звена первого порядка


или его уравнение движения


Характеристики звеньев этого типа носят монотонный характер, поэтому их также называют апериодическими звеньями первого порядка.

Графически она представляет собой экспоненту, начинающуюся на оси ординат в точке К/Т и асимптотически стремящуюся к 0. Внешний вид весовой функции позиционного звена первого порядка показан на Рис.46

(48)

(49)

Частотные характеристики строятся по выражению частотной передаточной функции звена



- действительная часть частотной ПФ,

- мнимая часть частотной ПФ,

- модуль частотной ПФ,

- аргумент частотной ПФ.

АФЧХ такого звена имеет вид

Рис.47

(50)

ЛАЧХ позиционных звеньев первого порядка является



ЛАХ может быть построена по точкам , вычисленным для различных значений частот или приближенно - в виде ломаных прямых (асимптот). Приближенная ЛАХ называется асимптотической.
Для ЛАХ звеньев этого типа могут быть найдены 2-е асимптоты, к которым стремится характеристика на
двух диапазонах частот, а именно: при , и , .
Аналитическое выражение первой асимптоты получается из выражения для при
, когда и 1, что позволяет пренебречь по сравнению с 1

Аналитическое выражение второй асимптоты получается из выражения для при
когда и 1, что позволяет пренебречь 1 по сравнению с

На плоскости логарифмических характеристик первая асимптота проходит параллельно оси частот на уровне , а вторая асимптота – под наклоном -20дб/дек через точку { ; = }

-20дб/дек

Асимптоты пересекаются в указанной точке. Частота = называется сопрягающей.
Действительная ЛАХ (красная линия) проходит ниже асимптотической, стремясь к ней при и
Максимальное отличие на = составляет






Что соответствует

(53)

порядка имеет вид ( Рис.49)

ЛФЧХ строится по выражению

(55)

К ним относятся звенья, описываемые уравнениями вида:





В зависимости от сочетания параметров передаточной функции звена их подразделяют на 3-и типа:
- апериодические звенья второго порядка;
- колебательные звенья второго порядка;
- консервативные звенья второго порядка.
1.3.1. Апериодические звенья второго порядка
К звеньям этого типа относят позиционные звенья второго порядка, параметры передаточной функции которых соотносятся: . Это условие, при котором корни характеристического уравнения звена
будут действительными.
,при подкоренное выражение

В этом случае характеристическое уравнение звена может быть представлено в виде:
где: , , а передаточная функция звена в виде:


Такая передаточная функция соответствует последовательному соединению двух апериодических звеньев первого порядка с передаточными функциями
и

поэтому эти звенья и называют апериодическими 2-го порядка или двойными апериодическими.

производную от переходной функции

Вид переходной характеристики представлен на Рис.50

Переходная функция

Временные характеристики звеньев второго порядка

Весовая функция

(58)

(59)

(60)

передаточной функции

- аргумент частотной передаточной функции

Частотная передаточная функция звеньев этого типа имеет вид

(61)

(62)

Аналитическое выражение ЛФХ:

(63)

параметров корни характеристического уравнения звена будут комплексно-сопряженными

Передаточная функция звеньев этого типа может быть представлена в виде:

При комплексно-сопряженных корнях характеристического уравнения и х(t)=1(t) решение дифференциального уравнения будет иметь вид:

получим:

т.е. реакция звена будет иметь затухающую гармоническую составляющую.

или используя формулы Эйлера:

, тем меньше затухание переходных процессов в звене и больше частота колебаний.

Рис.53

Рис.54

(68)

По экспериментально снятой характеристике можно найти параметры звена

Временные характеристики колебательных звеньев

Переходная характеристика звена может быть получена при подаче на его вход воздействия 1(t) или построена по выражению

Аналитическое выражение весовой функции

частотной передаточной функции

- аргумент частотной передаточной функции

Частотные характеристики колебательных звеньев

функция консервативного звена:

Весовая функция

Временные характеристики

Уравнением движения звеньев этого типа является уравнение вида:

1.3.3 Консервативные звенья

(73)

(74)

являются:

Построим ЛАХ и ЛФХ консервативного звена

(71)

(72)

Аналитическое выражение ЛФХ:

(73)

типа звеньев:
- идеальные интегрирующие звенья;
- реальные интегрирующие звенья;
- изодромные звенья.
2.1 Идеальные интегрирующие звенья
Выходная переменная звеньев этого типа пропорциональна не входному воздействию, а интегралу от входного воздействия, т. е. это звенья, которые при ряде допущений могут быть описаны уравнением вида:


Передаточная функция звеньев этого типа:

Временные характеристики идеальных интегрирующих звеньев
Переходная функция
При Х(t)=1(t) реакция звеньев этого типа представляет собой прямую из начала координат, с углом наклона, равным arctg K. Аналитическое выражение переходной характеристики идеальных интегрирующих звеньев имеет вид:
Графическое изображение переходной характеристики приведено на рис.59








Весовая функция является производной от переходной характеристики, а следовательно ее аналитическое выражение

Графическое изображение представлено на рис.60.

(74)

(75)

(76)

(77)

передаточная функция (амплитудно-фазовая характеристика) звеньев этого типа имеет аналитическое выражение вида:

Модуль частотной передаточной функции идеальных интегрирующих звеньев
Аргумент звеньев этого типа:

ЛАХ идеальных интегрирующих звеньев описывается выражением:



т.е. прямая, которая проходит через точки и имеет наклон
ЛФХ не зависит от частоты и является прямой, параллельной оси частот проходящей на уровне

-20дб/дек

К

-20дб/дек

(78)

(79)

(80)

ЛАХ и ЛФХ идеального интегрирующего звена приведены на Рис.61

последовательно, или в виде:

Используя последнее представление у(t), аналитическое выражение переходной характеристики получим как алгебраическую сумму решений уравнений идеального интегрирующего и апериодического 1-го порядка звеньев при Х(t)=1(t).

2.2 Реальные интегрирующие звенья (интегрирующие с запаздыванием)

Т

Весовая функция звена имеет выражение



Ее графическое изображение
приведено на Рис.63.

Т

К реальным интегрирующим звеньям относят звенья, которые описываются уравнениями вида:

Последнее выражение – уравнение 2-го порядка, у которого свободный член равен 0. Оно может быть представлено:

или системой двух уравнений

что соответствует параллельному соединению идеального интегрирующего и апериодического звена 1-го порядка.

Передаточная функция звеньев этого типа имеет вид:

Временные характеристики реальных интегрирующих звеньев

Переходная функция

(80)

(81)

В графическом виде она представлена на рис.62

(82)

КТ

(83)

и ,

при и .
ЛФХ строится по точкам, используя выражение:
.
ЛАХ и ЛФХ можно построить также как сумму соответствующих характеристик двух звеньев: идеального интегрирующего и апериодического 1-го порядка.

Частотные характеристики реальных интегрирующих звеньев

Частотная передаточная функция реальных интегрирующих звеньев


Модуль частотной передаточной функции реальных интегрирующих звеньев


Аргумент частотной передаточной функции реальных интегрирующих звеньев

ЛАХ строится по выражению:

-20дб/дек

-40дб/дек

(84)

(85)

(86)

к

1000

звеньям этого типа относят звенья, которые описываются уравнениями вида:
или в операторной форме
где
Передаточная функция изодромных звеньев имеет вид:
Из выражения для передаточной функции следует, что изодромное звено может быть представлено совокупностью двух параллельно включенных звеньев, а именно идеального интегрирующего и идеального статического с коэффициентами передачи К и К1 соответственно.
Временные характеристики изодромных звеньев
Переходная функция
Переходная характеристика изодромного звена - реакция звена на входное воздействие вида Х(t)=1(t)
может рассматриваться как сумма реакций двух звеньев: интегрирующего hи(t) и безынерционного hб(t).
Аналитическим выражением переходной характеристики является:

Графическое изображение переходной функции приведено на рис.65. Весовая функция изодромного звена - реакция звена на входное воздействие вида Х(t)= (t) имеет
аналитическое выражение производной от h(t) и равна сумме весовых функций указанных звеньев

К

wб(t)

wи(t)=К

Вид весовой функции изодромных звеньев приведен на рис.66

(87)

(88)

(89)

(90)

изодромных звеньев имеет вид:


Модуль частотной передаточной функции изодромных звеньев
Аргумент частотной передаточной функции реальных интегрирующих звеньев

ЛАХ звеньев этого типа строится по выражению:

Асимптотами ЛАХ изодромного звена являются
при и


при и

Асимптоты соответствуют:
- ЛАХ интегрирующего звена,
- ЛАХ безынерционного звена.
ЛФЧХ можно представить суммой ЛФХ интегрирующего звена и форсирующего звена .
ЛАХ и ЛФХ изодромного звена приведены на рис.67

0.01

-20дб/дек

0дб/дек

(91)

к

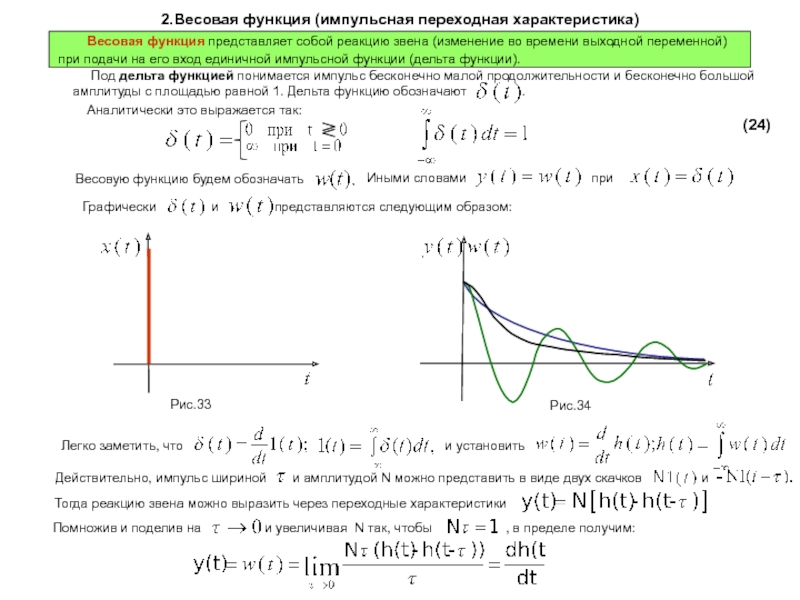
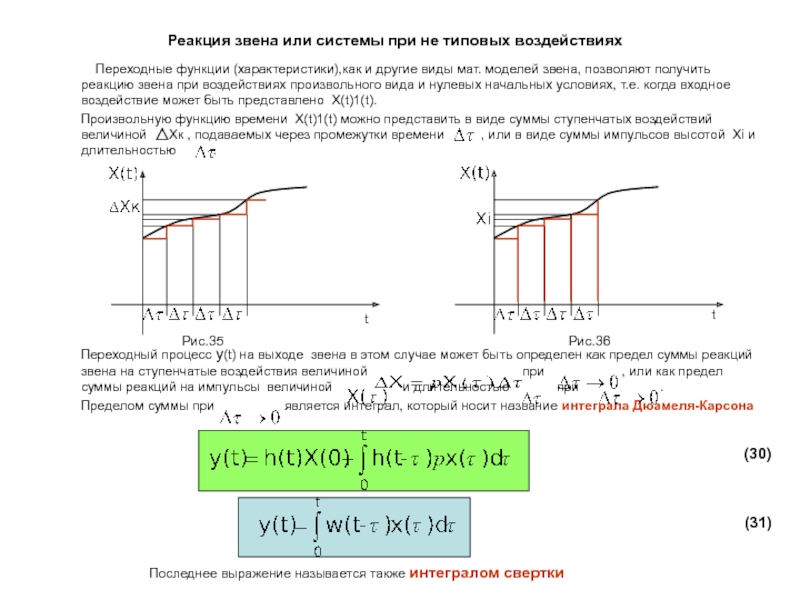
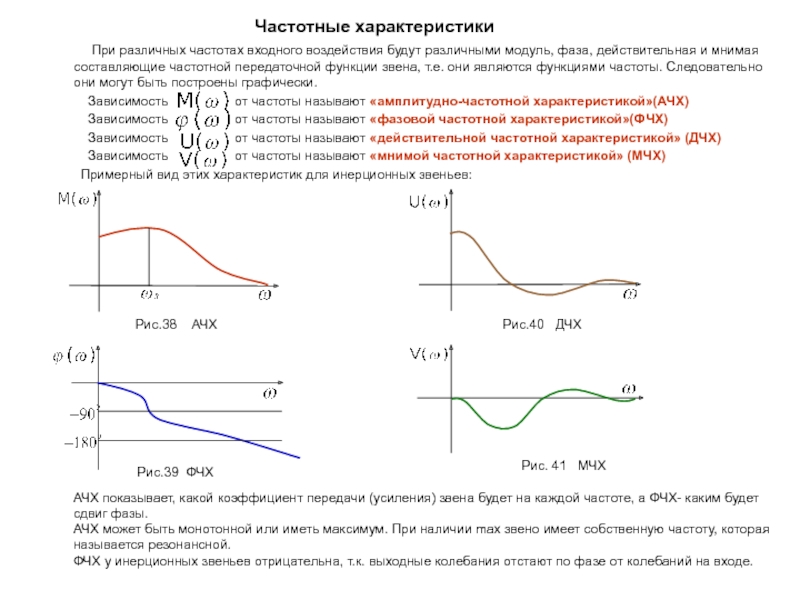
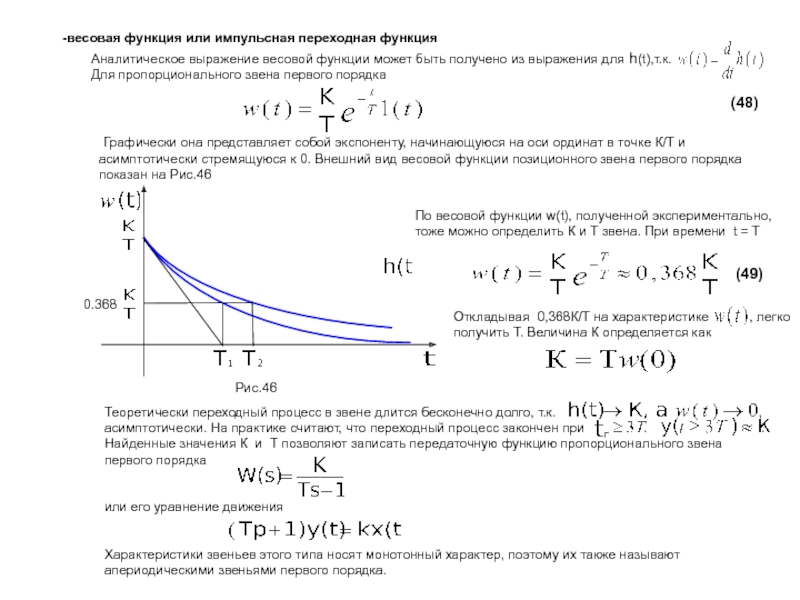
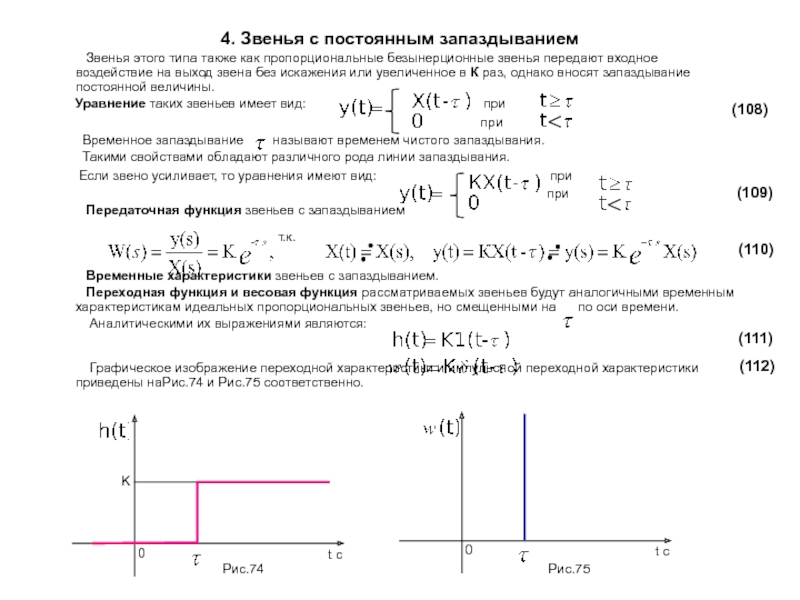
выходная переменная которых при определенных условиях пропорциональна производной от входного воздействия. Такие звенья и называют дифференцирующими.
К группе дифференцирующих звеньев относят два типа звеньев:
- идеальные дифференцирующие звенья;
- реальные дифференцирующие звенья (дифференцирующие с замедлением).
3.1 Идеальные дифференцирующие звенья
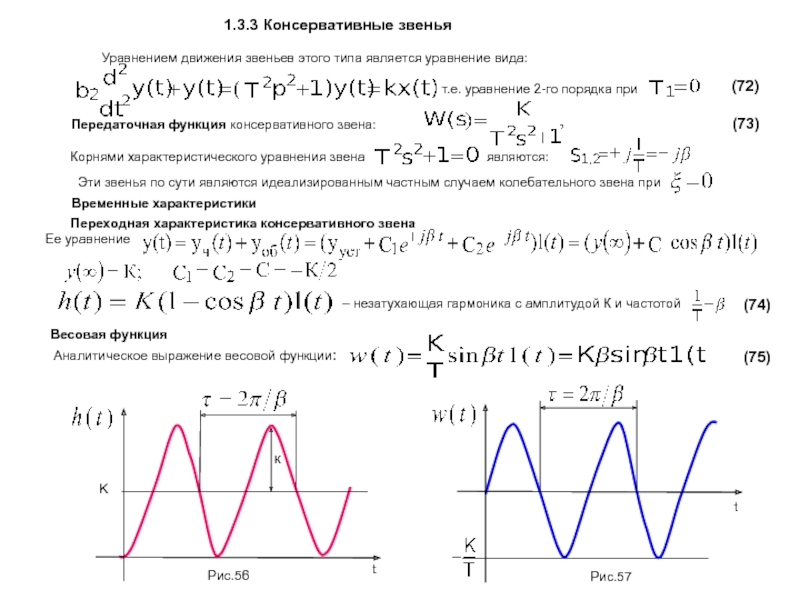
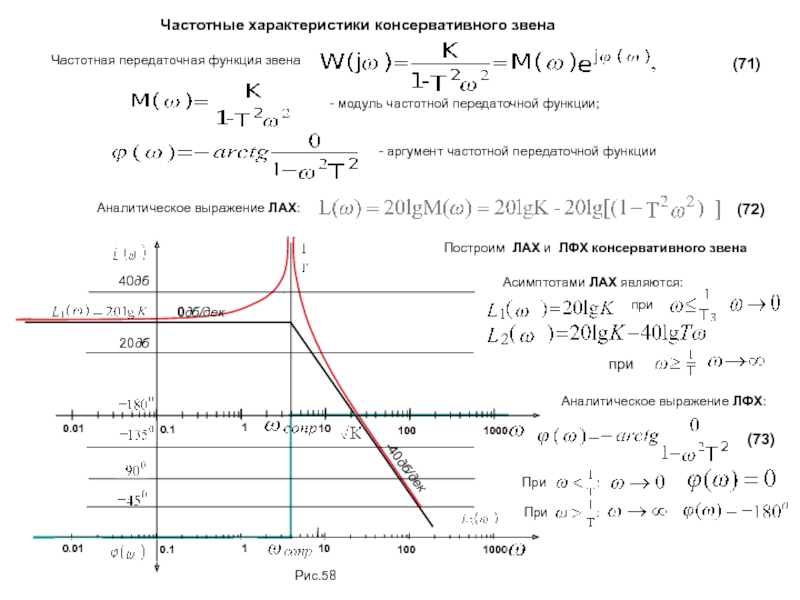
К звеньям этого типа относят звенья, которые описываются уравнениями вида:


Коэффициент передачи дифференцирующего звена размерная величина, которая содержит и размерность времени (сек).
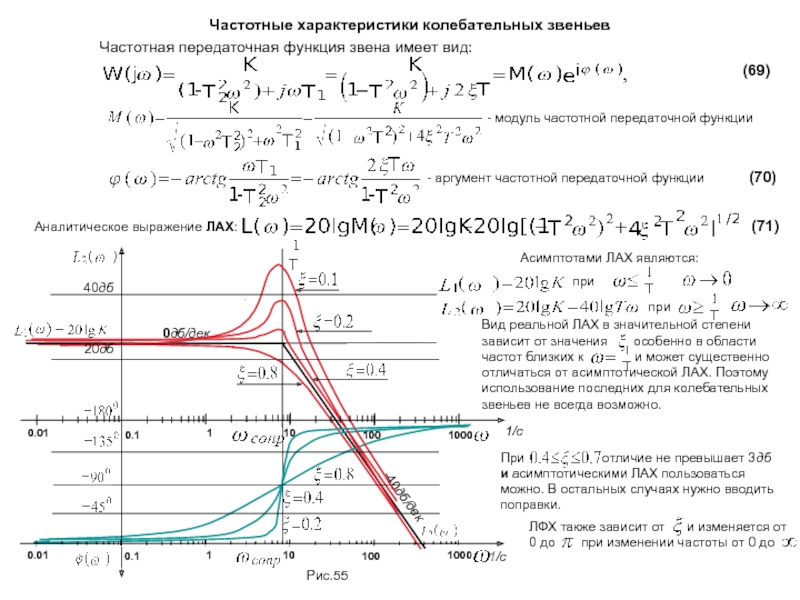
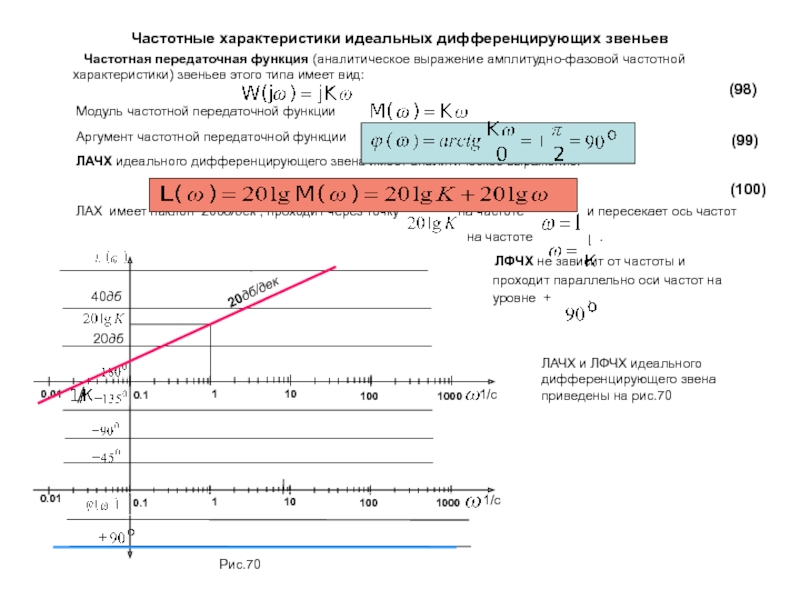
Передаточная функция идеальных дифференцирующих звеньев имеет вид:
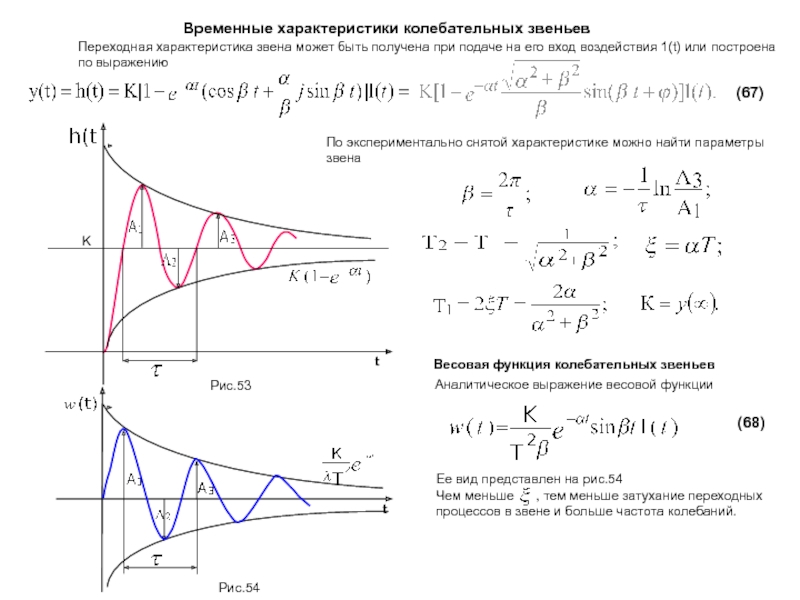
Временные характеристики идеальных дифференцирующих звеньев
Переходная функция идеального дифференцирующего звена
Реакцией звена на воздействие вида 1(t) будет увеличенная в К раз производная от воздействия этого вида, т.е. импульсом бесконечно большой амплитуды и бесконечно малой длительности, площадь которого равна К. Аналитическое выражение переходной функции:
Графическое ее представление приведено на рис.68.
Весовая функция идеального дифференцирующего звена
Она имеет аналитическое выражение вида:


Это соответствует двум импульсам бесконечно
малой длительности и положительной и
отрицательной бесконечно большой амплитуды
при времени равном 0 (см.Рис.69).

Рис.68

(94)

(95)

(96)

(97)

амплитудно-фазовой частотной характеристики) звеньев этого типа имеет вид:

Модуль частотной передаточной функции
Аргумент частотной передаточной функции
ЛАЧХ идеального дифференцирующего звена имеет аналитическое выражение:

ЛАХ имеет наклон 20дб/дек , проходит через точку на частоте и пересекает ось частот
на частоте .
ЛФЧХ не зависит от частоты и
проходит параллельно оси частот на
уровне + .

Частотные характеристики идеальных дифференцирующих звеньев

20дб/дек

ЛАЧХ и ЛФЧХ идеального дифференцирующего звена приведены на рис.70

(98)

(99)

(100)

этого типа имеют некоторую инерционность, поэтому дифференцируют входное воздействие с погрешностью, особенно ощутимой на больших частотах и при быстрых его изменениях во времени.
Уравнение реальных дифференцирующих звеньев имеет вид:



Вводя промежуточную переменную , звенья этого типа можно представить в виде последовательно соединенных двух звеньев: -идеально дифференцирующего и апериодического 1-го порядка, т.е они не являются элементарными типовыми звеньями.



Передаточная функция реальных дифференцирующих звеньев имеет вид:
Временные характеристики реальных дифференцирующих звеньев
Переходная характеристика как решение дифференциального уравнения звена при Х(t)=1(t) имеет выражение вида:


т. е. импульс амплитудой К/Т со сглаженным задним фронтом, изменяющемся во времени по экспоненте.
.
Весовая функция звена
описывается выражением:

Переходная и весовая функции звена представлены на рис.71 и рис.72 соответственно.

(101)

(102)

(103)

(104)

Частотная передаточная функция (аналитическое выражение амплитудно-фазовой частотной характеристики) реальных дифференцирующих звеньев имеет вид:



Модуль частотной ПФ -


Аргумент частотной ПФ -

ЛАХ звена имеет аналитическое выражение:

Асимптотами ЛАХ звена являются

при и

при и

Асимптоты соответствуют:
- ЛАХ идеального
дифференцирующего звена,
- ЛАХ безынерционного звена.

ЛФЧХ можно представить суммой ЛФХ идеального дифференцирующего звена и апериодического звена 1-го порядка.
ЛАХ и ЛФХ реального дифференцирующего звена приведены на рис.73.

1/с

20дб/дек

0дб/дек

(105)

пропорциональные безынерционные звенья передают входное воздействие на выход звена без искажения или увеличенное в К раз, однако вносят запаздывание постоянной величины.
Уравнение таких звеньев имеет вид: при
при
Временное запаздывание называют временем чистого запаздывания.
Такими свойствами обладают различного рода линии запаздывания.
Если звено усиливает, то уравнения имеют вид: при
при
Передаточная функция звеньев с запаздыванием
т.к.

Временные характеристики звеньев с запаздыванием.
Переходная функция и весовая функция рассматриваемых звеньев будут аналогичными временным характеристикам идеальных пропорциональных звеньев, но смещенными на по оси времени.
Аналитическими их выражениями являются:

Графическое изображение переходной характеристики и импульсной переходной характеристики приведены наРис.74 и Рис.75 соответственно.

4. Звенья с постоянным запаздыванием

(108)

(109)

(110)

(111)

(112)

сигнал на выходе звена будет
гармоническим, но сдвинутым на по оси времени .
Амплитуда выходного сигнала звена будет равна Хm у звеньев чистого запаздывания или KXm при усилении звеном в К раз, следовательно модуль звена или соответственно. Фазовое запаздывание Т – период.
Частотные свойства звеньев с запаздыванием можно
представить в экспоненциальном виде

для звеньев
с усилением
ЛАХ звена с запаздыванием имеет выражение:


если
звено с усилением.
ЛФХ будет нелинейной монотонно убывающей
функцией частоты, т.к. , а при
построении ЛФХ используется логарифмический
масштаб.
ЛАХ и ЛФХ звеньев с запаздыванием приведены
на Рис.77.

Частотные характеристики звеньев с запаздыванием

(113)

(114)

(115)

при и , хотя их описание с точностью до знаков некоторых коэффициентов полинома B(s) передаточной функции будут совпадать с устойчивыми звеньями. Такие звенья называются неустойчивыми.

Исключение составляют интегрирующие звенья, реакция которых на скачок воздействия (переходная функция) неограниченно возрастает при . В тоже время производная от стремится к постоянному значению (как весовая функция). Такие звенья называют нейтрально устойчивыми.

Неустойчивые и неминимально - фазовые звенья

Рассмотренные ранее звенья называются устойчивыми и минимально – фазовыми, так как при подаче на их вход воздействия ограниченной величины выходная переменная стремится к установившемуся значению, а при подаче гармонического воздействия фазовый сдвиг сравнительно небольшой.

Различие в поведении устойчивых и неустойчивых звеньев можно объяснить, используя решение уравнения движения звена вида :

Корни характеристического уравнения звена называются полюсами или нулями знаменателя передаточной функции. Эти значения Si обращают полином знаменателя передаточной функции в 0 и являются коэффициентами в показателе степени экспонент в решении уравнения движения звена.

Характеристическим уравнением называется приравненный нулю знаменатель передаточной функции.

движения и передаточные функции которых имеют вид:

Пример устойчивого и неустойчивого звеньев

Признаком неустойчивых звеньев является отрицательное значение одного из коэффициентов полинома знаменателя передаточной функции. Неустойчивыми будут звенья с передаточными функциями:

т.е.неограниченно возрастает по экспоненциальной зависимости.

(118)

(116)

их амплитудно-частотные характеристики совпадают с АЧХ устойчивых звеньев, а фазовые сдвиги значительно больше, особенно на низких частотах.

Модуль частотной передаточной функции неустойчивого звена равен модулю частотной ПФ устойчивого звена первого порядка.

Следовательно АЧХ и ЛАЧХ этих звеньев будут совпадать.

Аргумент устойчивого звена будет определяться выражением:

ЛАЧХ и ЛФЧХ этих звеньев приведены на Рис.79.

-20дб/дек

Большие фазовые сдвиги имеют и звенья с положительными корнями полинома А(s) числителя ПФ. Корни полинома числителя называют нулями. Если

и

(119)

(120)

схему САР, работающих по замкнутому циклу, можно представить в виде:

Рис.80

Условные обозначения:

называется передаточной функцией разомкнутой системы по управляющему воздействию.

называется передаточной функцией разомкнутой системы по возмущающему воздействию.

Предположим, что ЧЭ имеет коэффициент передачи равный 1 и пока отсоединен от регулятора.

(122)

(123)

замыкания в уравнение (125) и решая относительно регулируемой переменной получим:

(126)

(127)

Или для изображений

Для замкнутой системы с учетом введенных понятий ПФ запишем

- называется передаточной функцией замкнутой системы по управляющему воздействию.

- называется передаточной функцией замкнутой системы по возмущающему воздействию.

(128)

(129)

(130)

уравнение для ошибки замкнутой САР:

Переходя в уравнении (131) от переменных во времени к их изображениям по Лапласу, введем более строгое понятие передаточных функций для ошибки

Уравнения (128), (129), (133) и (134) позволяют найти передаточные функции замкнутой системы при известных передаточных функциях разомкнутой системы. Легко найти выражения и для решения обратной задачи:

- характеристический полином замкнутой системы.

звеньев.

1.2 Перестановка звеньев:

1.1 Объединение цепочки звеньев: передаточная функция цепочки последовательно соединенных звеньев равна произведению передаточных функций этих звеньев.

2 Преобразование цепочки параллельно соединенных звеньев.

Передаточная функция цепочки последовательно соединенных звеньев равна сумме передаточных функций этих звеньев.

звеньев прямой и обратной цепи или направления замыкания контура

Передаточная функция контурно соединенных звеньев равна отношению передаточной функции прямой цепи к алгебраической сумме 1 и произведения передаточных функций звеньев прямой и обратной цепи контура.

на его вход

4.2 Со входа звена на его выход

4.3 переход к единичной обратной связи

его вход

5.2 Со входа звена на его выход

6. Перенос узла (точки ветвления) через сумматор (элемент сравнения)

6.1 С выхода сумматора на вход

6.2 Со входа сумматора на выход

7. Объединение и перестановка сумматоров

От перемены мест слагаемых сумма не изменяется