- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основні визначення. Характеристики надійності об'єкта презентация
Содержание
- 1. Основні визначення. Характеристики надійності об'єкта
- 2. Якісні характеристики надійності Працездатність — властивість об'єкта
- 3. Якісні характеристики надійності Напрацювання — тривалість (в
- 4. Кількісні характеристики надійності Основні кількісні характеристики надійності
- 5. Кількісні характеристики надійності Імовірність безвідмовної роботи P(t)
- 6. Кількісні характеристики надійності Частота відмов f(t) або
- 7. Кількісні характеристики надійності Небезпека відмови(невідновлювані) і параметр
- 8. Кількісні характеристики надійності Оскільки відмови елементів обладнання
- 9. Структурна надійність системи Послідовне з'єднання
- 10. Структурна надійність системи Паралельне з'єднання У випадках,
- 11. Структурна надійність системи Система з залежними елементами
- 12. Структурна надійність системи Розрахуємо ймовірність Р(А2). Для
- 13. Структурна надійність системи Після підстановки в Р(t)
- 14. Структурна надійність системи Резервування перемиканням на запасний
- 15. Структурна надійність системи А — в працездатному
- 16. Структурна надійність системи Резервування по методу
- 17. Структурна надійність системи Якщо всі детектори є
- 18. Структурна надійність системи Щоб зменшити кількість хибних
- 19. Структурна надійність системи При m = 1,
- 20. Розрахунок норм надійності Ядерна енергетична установка несе
- 21. Розрахунок норм надійності Визначення норм надійності для
- 22. Розрахунок норм надійності Якщо задана ймовірність безвідмовної
- 23. Розрахунок норм надійності Таким чином максимально припустима
Слайд 1Основні визначення
Надійність — властивість об'єкта зберігати у часі та в заданих
характеризують здатність об'єкта виконувати функції, які вимагаються від об'єкта в заданих режимах і умовах застосування, технічного обслуговування, ремонтів, зберігання і транспортування.
З визначення маємо, що надійність це:
властивість (якісна характеристика)
здатність виконувати поставлені функції (функціональна характеристика).
Слайд 2Якісні характеристики надійності
Працездатність — властивість об'єкта виконувати задані функції з параметрами
Довговічність — властивість об'єкта зберігати працездатність з необхідними перервами на технічне обслуговування і ремонти до граничного стану.
Граничний стан — поломка, граничний знос, чи зниження ефективності, зниження точності чи порушення норм техніки безпеки
Строк експлуатації (служби) — календарна тривалість експлуатації виробу до моменту досягнення граничного стану.
Слайд 3Якісні характеристики надійності
Напрацювання — тривалість (в годинах чи циклах) чи об'єм
Ресурс — напрацювання до граничного стану; ресурс дорівнює суммі всіх напрацюваннь від початку експлуатації до моменту досягнення граничного стану.
Відмова — подія, після якої об'єкт (повністю чи частково) престає виконувати покладені на нього (передбачені) функції. Відмова є випадковою подією.
Розрізняють об'єкти, що працюють до першої відмови - невідновлювані; ті, що підлягають ремонту - називаються відновлюваними.
Слайд 4Кількісні характеристики надійності
Основні кількісні характеристики надійності
Імовірність безвідмовної роботи P(t);
Імовірність
Частота відмов f(t);
Небезпека відмови λ(t);
Середнє напрацювання до першої відмови Tср.
Імовірністю відмови називається ймовірність того, що за певних умов експлуатації в заданому інтервалі часу виникне хоча б одна відмова.
Слайд 5Кількісні характеристики надійності
Імовірність безвідмовної роботи P(t)
Ймовірність безвідмовної роботи P(t) - ймовірність
Ймовірність P(t) прийнято називати надійністю в вузькому сенсі, в той час як надійність, за наведеним означенням, є надійнісю в широкому сенсі.
Слайд 6Кількісні характеристики надійності
Частота відмов f(t) або a(t) є щільністю ймовірності часу
Напрацюванням на відмову Tср називається математичне сподівання M[t] часу роботи до відмови. Математичне сподівання, тобто , обчислюється за частотою відмов (щільність розподілу часу безвідмовної роботи) так
Слайд 7Кількісні характеристики надійності
Небезпека відмови(невідновлювані) і параметр потоку відмов (відновлювані)
Зазвичай вироби проходять
період приробочних відмов;
період так званих раптових відмов;
період старіння.
Типова залежність λ-характеристики від часу
Слайд 8Кількісні характеристики надійності
Оскільки відмови елементів обладнання ЯЕУ є, зазвичай, рідкісними подіями,
Якщо кількість відмов виробу підлягає стаціонарному розподілу Пуасона, то говорять, що виробу властива експоненційна надійність, в такому випадку:
P(t)=exp(-λt)
Структурна надійність системи — результуюча надійність системи при заданій її структурі і відомих надійностях всіх частин(елементів), що входять до неї. Частини, з яких складається система, показники яких відомі, називаються елементами розрахунку надійності.
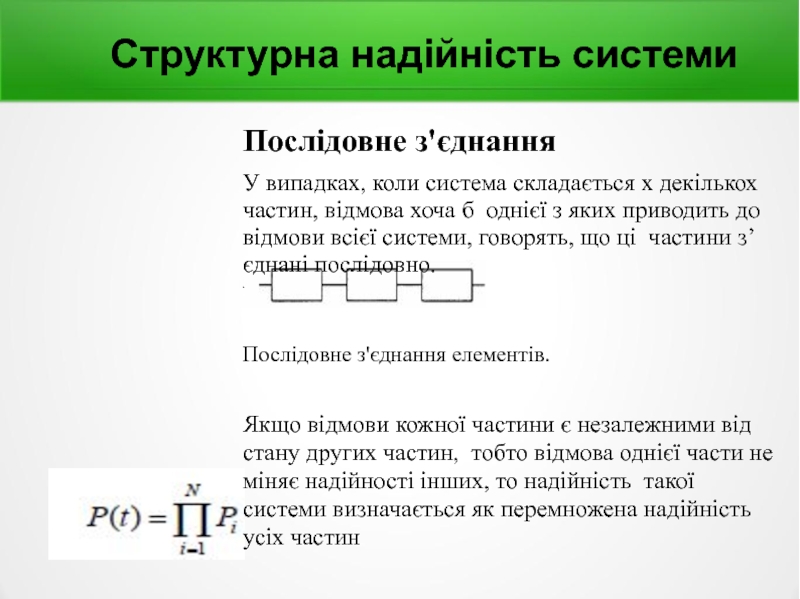
Слайд 9Структурна надійність системи
Послідовне з'єднання
У випадках, коли система складається х декількох частин,
.
Послідовне з'єднання елементів.
Якщо відмови кожної частини є незалежними від стану других частин, тобто відмова однієї части не міняє надійності інших, то надійність такої системи визначається як перемножена надійність усіх частин
Слайд 10Структурна надійність системи
Паралельне з'єднання
У випадках, коли система складається з декількох частин
.
Якщо відмови кожної частини незалежні від стану других частин, тобто відмова однієї части не міняє надійності інших, то ймовірність F(t) =1− P(t) відмови системи рівна перемноженим ймовірностям відмови всіх її частин:
Паралельне з'єднання елементів.
Слайд 11Структурна надійність системи
Система з залежними елементами
Розглянемо випадок залежності ймовірності відмови одних
Р(t) = Р(А) = Р(А1) + Р(А2) + Р(А3)
λ1(2) – небезпека відмови першого(другого) елемента;
λ12(21) – небезпека відмови першого(другого) елемента за умови , що другий(перший) вийов з ладу
Подія А , полягає в тому, що система не вийде з ладу протягом часу t складається з 3 несумісних подій:
A1 – за час t не вийшов з ладу ні 1 елемент;
А2 – за час t перший елемент вийшов з ладу, а другий не вийшов A3 – за час t другий елемент вийшов з ладу, а перший не вийшов; Очевидно, що
.
Слайд 12Структурна надійність системи
Розрахуємо ймовірність Р(А2). Для цього знайдемо ймовірність dР2, того,
елемент вийде з ладу в інтервалі часу dτ τє(0, t), а другий елемент залишиться справним, щоб задовольнити умови треба:
обидва елемента залишились справними до момента часу τ
перший елемент відмовив в момент часу τ
другий елемент не відмовив за залишок часу
Отримуємо за аналогією Р(А3)
Слайд 13Структурна надійність системи
Після підстановки в
Р(t) = Р(А) = Р(А1) + Р(А2)
отримуємо
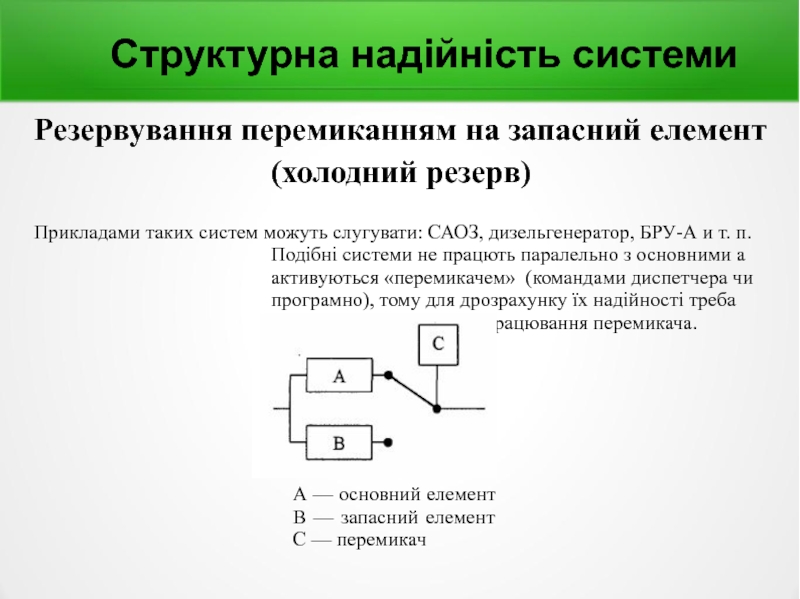
Слайд 14Структурна надійність системи
Резервування перемиканням на запасний елемент (холодний резерв)
Прикладами таких систем
А — основний елемент В — запасний елемент С — перемикач
Слайд 15Структурна надійність системи
А — в працездатному стані основний елемент; В —
S — невключення в роботу запасного елемента без відмови основного; D — включення в роботу запасного елемента після відмови основного;
Тоді система буде працездатною за при виконанні данного логічного виразу
Де Р(t), ймовірність працездатності системи
fA ,fB— густини розподілу безвідмовної роботиелементів А і В відповідно
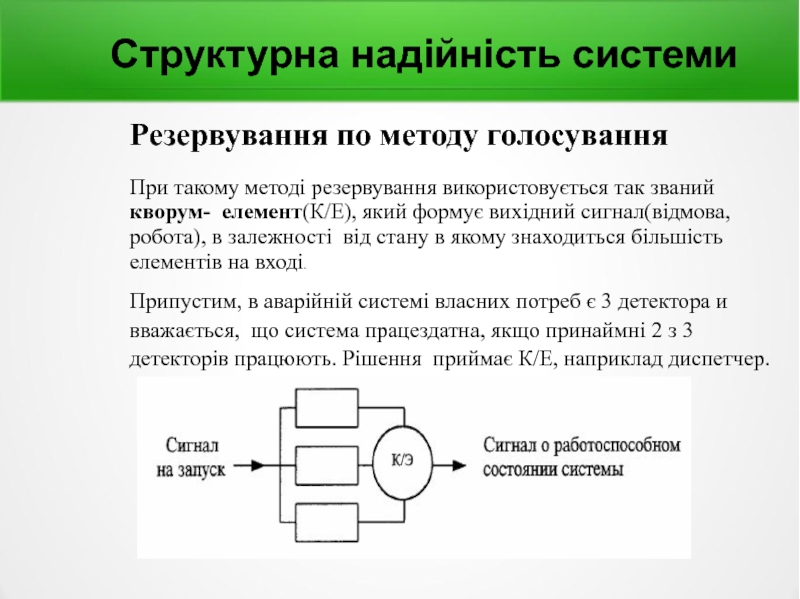
Слайд 16Структурна надійність системи
Резервування по методу голосування
При такому методі резервування використовується так
Припустим, в аварійній системі власних потреб є 3 детектора и вважається, що система працездатна, якщо принаймні 2 з 3 детекторів працюють. Рішення приймає К/Е, наприклад диспетчер.
Слайд 17Структурна надійність системи
Якщо всі детектори є рівнонадійними, то надійність резерву
P2/3 =
У разі використання звичайного паралельного з'єднання
Рп = 1 – (1 – Р)³ = 3Р –3Р² + Р³ ≈ Р.
Данна схема створена для проведення профілактичних робіт на обладнанні і оскільки величина Р близька до одиниці втрати за рахунок дублювання компенсуються підвищенням Р за рахунок профілактик.
Оскільки кворум-елемент також може відмовляти, означимо ймовірність його відмови за q, тоді його надійність рк = 1-q, таким чином кінцева формула:
Pзаг=ркР²(3 – 2Р)
Слайд 18Структурна надійність системи
Щоб зменшити кількість хибних спрацюваннь аварійного захисту, функціонує логіка
При m = 1, ймовірність хибного спрацювання:
Рхибне повне=1-(1-Рхибне)³≈ 3Рхибне
При m = 2, ймовірність хибного спрацювання:
P2/3 хибне = P³х + 3(1 – Рх)Р²х= Р²х(3 – 2Рх) ≈ 3Р²х.
Рхибне – ймовірність формування хибного сигналу
Слайд 19Структурна надійність системи
При m = 1, ймовірність неспрацювання у випадку наявності
Рн повне=1-Рн³
При m = 2, ймовірність неспрацювання у випадку наявності небезпеки:
P2/3 н = 1-Рн³ – 3Рн²(1 – Рн)
Рн – ймовірність невипрацювання сигналу у випадку небезпеки
Слайд 20Розрахунок норм надійності
Ядерна енергетична установка несе в собі велику потенційну загрозу,
Слайд 21Розрахунок норм надійності
Визначення норм надійності для приладу та його елементів проводиться,
закон зміни в часі — експоненційний, тобто розглядаються лише раптові відмови і недезпека відмови обладнання не залежить від часу;
всі елементи рівнонадійні;
всі елементи включені послідовно.
Вхідними данними для проведення розрахунків являються:
-Кількість елементів розрахунку надійності(блоків, вузлів, пристроїв і т. п.);
-Заданий час неперервної справної роботи, з заданою ймовірністю Pн(t).
Слайд 22Розрахунок норм надійності
Якщо задана ймовірність безвідмовної роботи Рн, то
,де Рі ймовірність
Оскільки ми припустили, що всі елементи мають однакову надійність, отримаємо:
При експоненційному законі надійності
,де λ допустима небезпека відмови для виробу.
Слайд 23Розрахунок норм надійності
Таким чином максимально припустима небезпека відмови для елемента
λi=λ/N
Варто пам'яти,
λi ≥ ∑λj
У випадку, якщо нерівність не виконується, то вікористовують різні способи підвищення надійності(резрвування, облегчення режимів експлуатації)