- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Метод векторной диаграммы. Сложение гармонических колебаний. Биения презентация
Содержание
- 1. Метод векторной диаграммы. Сложение гармонических колебаний. Биения
- 2. Общая физика. «Физика колебаний и волн»
- 3. Общая физика. «Физика колебаний и волн»
- 4. Общая физика. «Физика колебаний и волн»
- 5. Общая физика. «Физика колебаний и волн»
- 6. Общая физика. «Физика колебаний и волн»
- 7. Общая физика. «Физика колебаний и волн»
- 8. Общая физика. «Физика колебаний и волн»
- 9. Общая физика. «Физика колебаний и волн» Амплитуда Биения
- 10. Общая физика. «Физика колебаний и волн»
- 11. Общая физика. «Физика колебаний и волн»
- 12. Общая физика. «Физика колебаний и волн»
- 13. Общая физика. «Физика колебаний и волн»
- 14. Общая физика. «Физика колебаний и волн»
- 15. Общая физика. «Физика колебаний и волн»
- 16. Общая физика. «Физика колебаний и волн» Дифференциальное уравнение свободных затухающих колебаний:
- 17. Общая физика. «Физика колебаний и волн»
- 18. Общая физика. «Физика колебаний и волн»
- 19. Общая физика. «Физика колебаний и волн»
- 20. Общая физика. «Физика колебаний и волн»
Слайд 1Общая физика. «Физика колебаний и волн»
ЛЕКЦИЯ 8
ПЛАН ЛЕКЦИИ
Метод векторной диаграммы.
Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу.
Свободные затухающие колебания.
Слайд 2Общая физика. «Физика колебаний и волн»
Метод векторной диаграммы
Графическое изображение
Закон изменения координаты проекции со временем:
Слайд 3Общая физика. «Физика колебаний и волн»
Гармоническое колебание может быть задано
Слайд 4Общая физика. «Физика колебаний и волн»
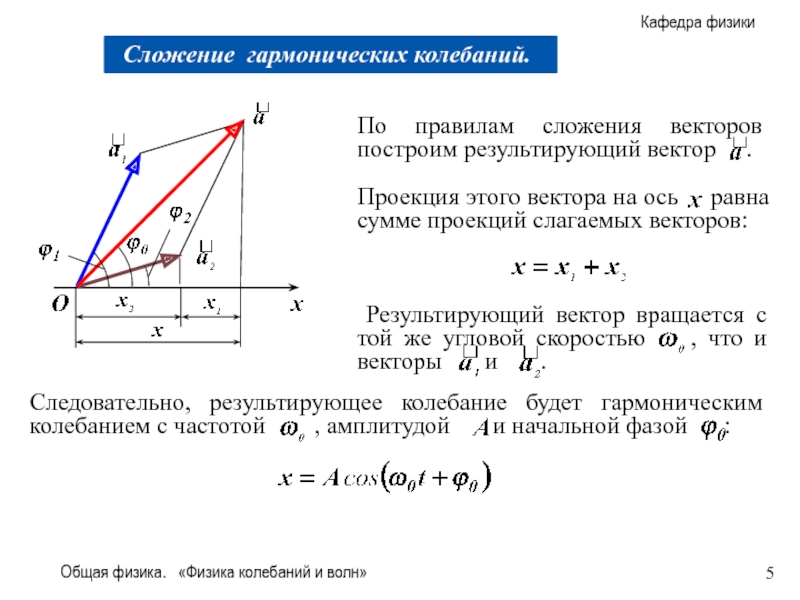
Сложим два гармонических колебания одинакового
Определим вид и параметры результирующего колебания. Воспользуемся методом векторной диаграммы.
Слайд 6Общая физика. «Физика колебаний и волн»
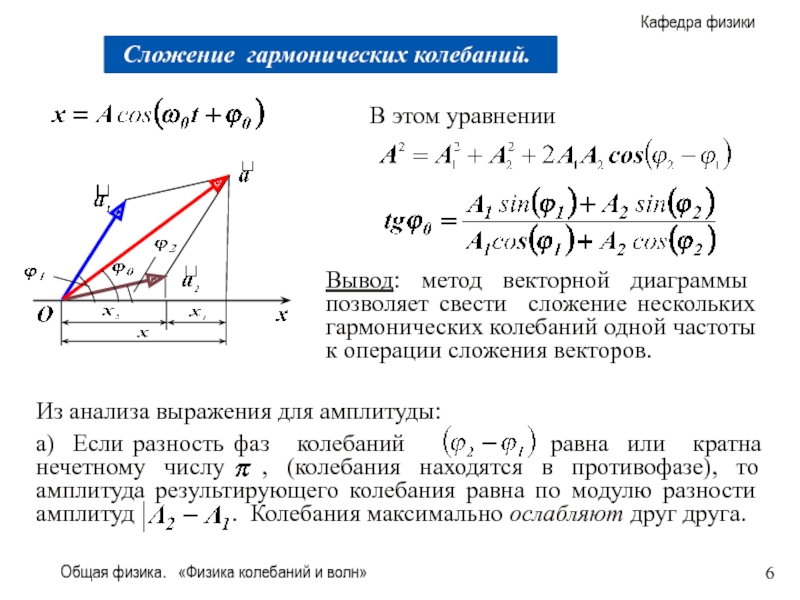
В этом уравнении
Вывод: метод
Из анализа выражения для амплитуды:
Слайд 7Общая физика. «Физика колебаний и волн»
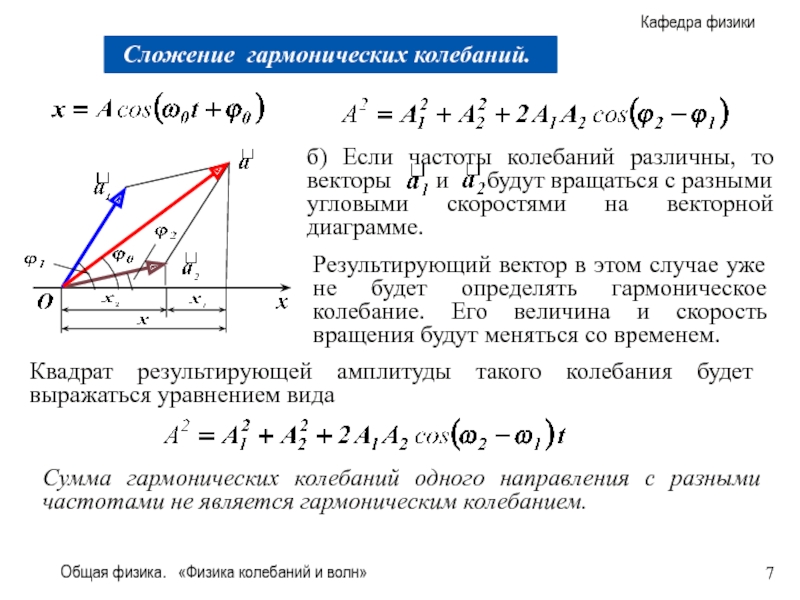
Результирующий вектор в этом случае
Квадрат результирующей амплитуды такого колебания будет выражаться уравнением вида
Сумма гармонических колебаний одного направления с разными частотами не является гармоническим колебанием.
Слайд 8Общая физика. «Физика колебаний и волн»
Пусть два складываемых гармонических колебания
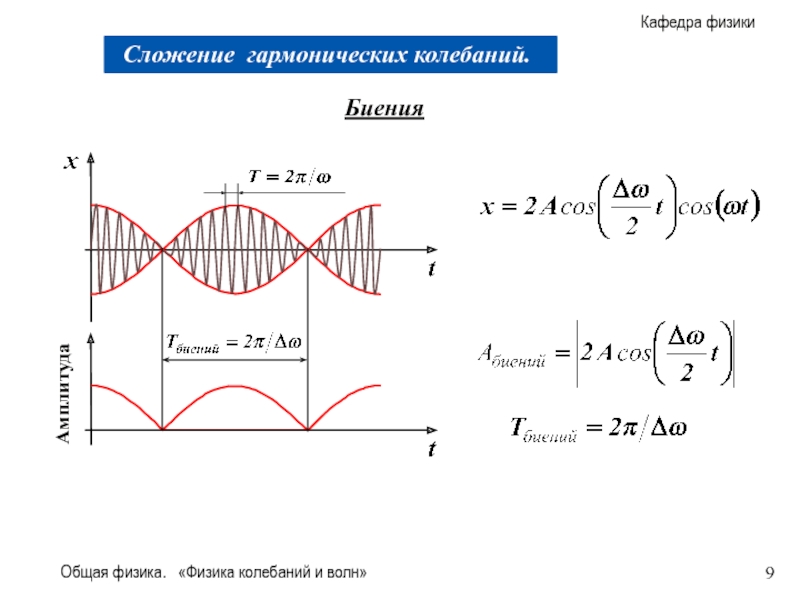
Биения
Имеются два колебания, различающиеся только частотами:
Результат сложения колебаний:
Слайд 10Общая физика. «Физика колебаний и волн»
Сложение взаимно перпендикулярных колебаний.
Рассмотрены
Сложение разнонаправленных колебаний - более сложный случай.
Пример: на управляющие вертикальные и горизонтальные пластины осциллографа поданы периодические гармонические сигналы.
Пусть начальная фаза первого колебания равна нулю. Уравнения колебаний:
Слайд 11Общая физика. «Физика колебаний и волн»
Сложение взаимно перпендикулярных колебаний.
Для
После преобразований:
Анализ:
Слайд 12Общая физика. «Физика колебаний и волн»
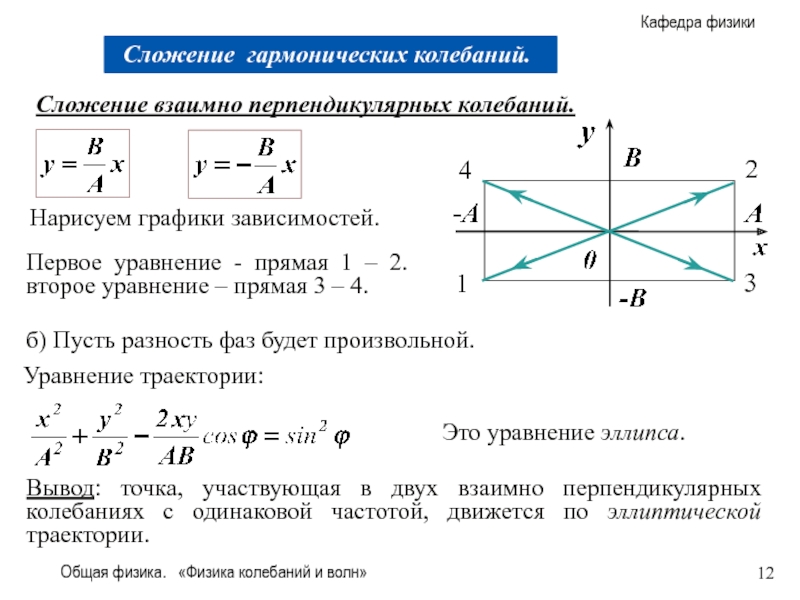
Сложение взаимно перпендикулярных колебаний.
Нарисуем
Первое уравнение - прямая 1 – 2. второе уравнение – прямая 3 – 4.
1
4
3
2
б) Пусть разность фаз будет произвольной.
Уравнение траектории:
Это уравнение эллипса.
Вывод: точка, участвующая в двух взаимно перпендикулярных колебаниях с одинаковой частотой, движется по эллиптической траектории.
Слайд 13Общая физика. «Физика колебаний и волн»
Сложение взаимно перпендикулярных колебаний.
Параметры
Это каноническое уравнение эллипса
Полуоси эллипса равны соответствующим амплитудам колебаний.
Слайд 14Общая физика. «Физика колебаний и волн»
Сложение взаимно перпендикулярных колебаний.
Если
Уравнения колебаний имеют вид:
Результирующее колебание показано на рисунке.
Траектория вырождается в незамкнутую кривую, по которой точка движется туда и обратно. Это одна из простейших фигур Лиссажу.
Слайд 15Общая физика. «Физика колебаний и волн»
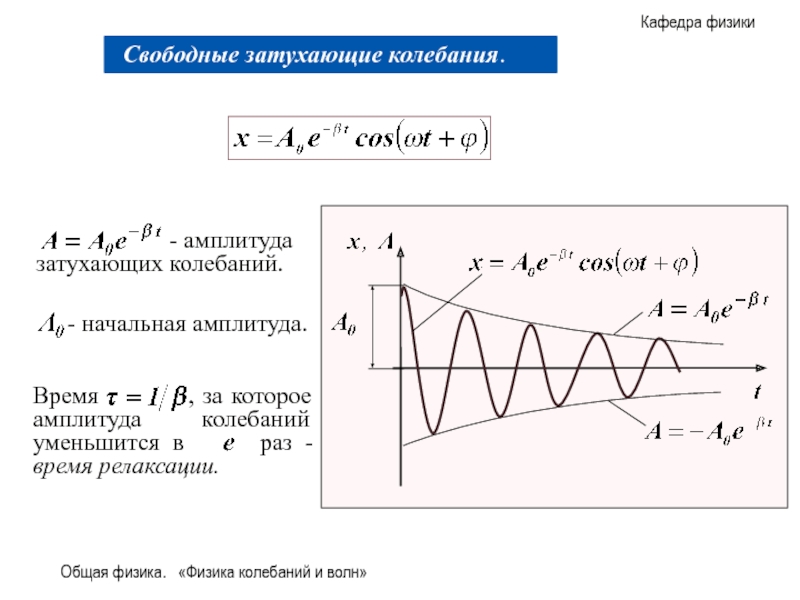
В реальных системах всегда присутствуют
Рассмотрим законы изменения параметров свободных затухающих колебаний.
Свободные затухающие колебания – это такие свободные колебания, амплитуда которых из-за потерь энергии реальной колебательной системой с течением времени уменьшается.
Закон затухания колебаний определяется свойствами колебательных систем.
Слайд 16Общая физика. «Физика колебаний и волн»
Дифференциальное уравнение свободных затухающих колебаний:
Слайд 18Общая физика. «Физика колебаний и волн»
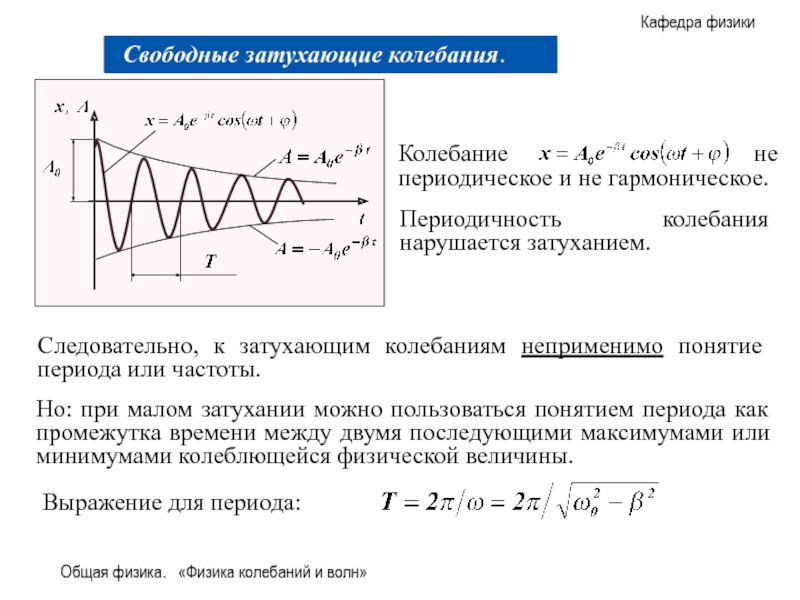
Периодичность колебания нарушается затуханием.
Следовательно,
Но: при малом затухании можно пользоваться понятием периода как промежутка времени между двумя последующими максимумами или минимумами колеблющейся физической величины.
Выражение для периода:
Слайд 19Общая физика. «Физика колебаний и волн»
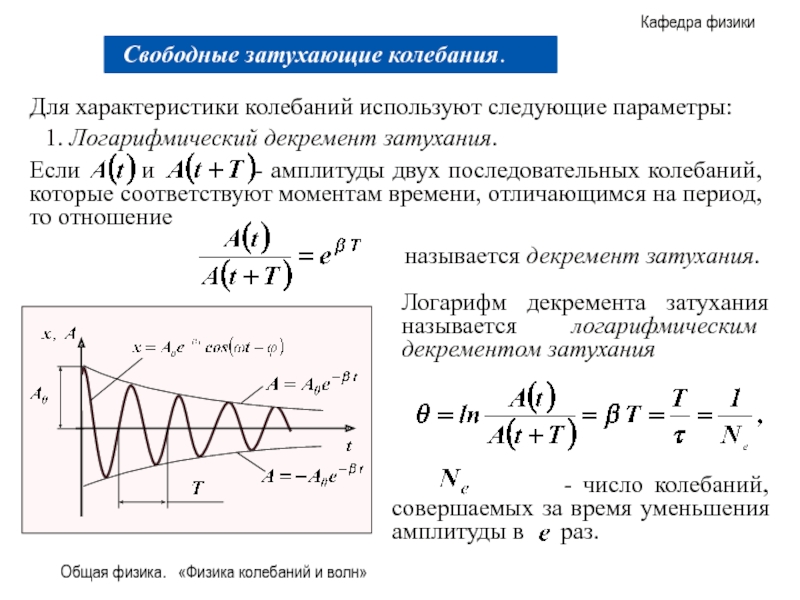
Для характеристики колебаний используют следующие
1. Логарифмический декремент затухания.
называется декремент затухания.
Логарифм декремента затухания называется логарифмическим декрементом затухания
Слайд 20Общая физика. «Физика колебаний и волн»
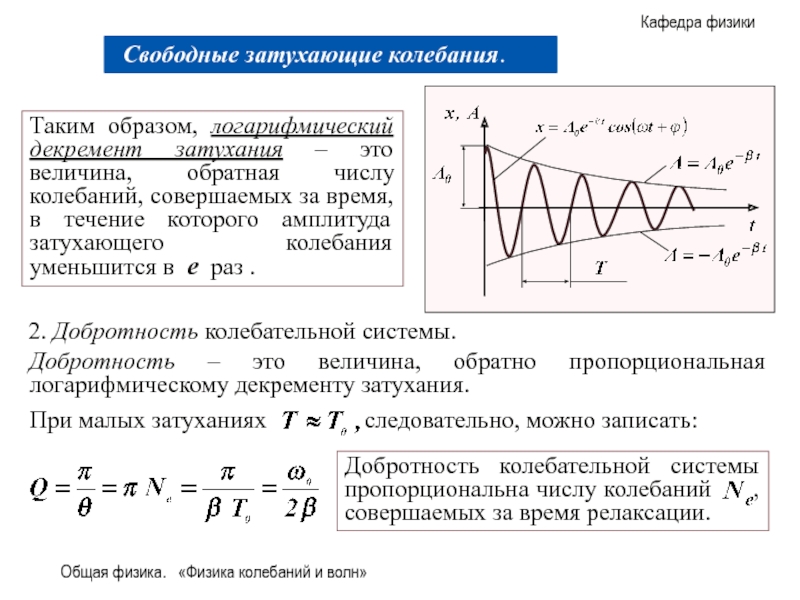
Таким образом, логарифмический декремент затухания
2. Добротность колебательной системы.
Добротность – это величина, обратно пропорциональная логарифмическому декременту затухания.