- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Механика сплошных сред. Введение в гидродинамику презентация
Содержание
- 1. Механика сплошных сред. Введение в гидродинамику
- 2. Преподаватель: Черняк Владимир Григорьевич Объем курса
- 3. Цель: Изучить основы гидродинамики. Получить навыки
- 4. Введение Гидродинамика – раздел механики сплошных сред,
- 5. Жидкость называют несжимаемой, если ее плотность одинакова
- 6. Так, например, если воду поместить в цилиндр
- 7. Многочисленные экспериментальные и теоретические исследования показывают, что
- 8. Свойства жидкости Давление жидкости – скалярная физическая
- 9. Здесь F – сила, с которой жидкость
- 10. Закон Паскаля: В любой точке покоящейся жидкости
- 11. Внесистемные единицы: 1 мм рт. ст. (торр)
- 12. Вязкость жидкости – свойство жидкости оказывать сопротивление
- 13. Основной закон вязкого движения жидкости был установлен
- 14. Кинематическая вязкость: где ρ -
- 15. Вязкость некоторых жидкостей при температуре 300 К:
- 16. Коэффициент динамической вязкости плотных газов и жидкостей
- 17. Уравнение неразрывности Плотность потока массы – масса
- 18. Баланс массы Мысленно выделим в жидкости фиксированный
- 20. Скорость изменения массы жидкости в объеме за
- 21. Скорость накопления массы в выделенном элементе объема
- 22. В результате получим или
- 23. Таким образом, уравнение неразрывности – уравнение баланса
- 24. В стационарном случае уравнение неразрывности имеет вид:
Слайд 2Преподаватель:
Черняк Владимир Григорьевич
Объем курса – 34 часа
Лекции – 17 часов
Практика –
17 часов
Отчетность – дифференцированный зачет
Отчетность – дифференцированный зачет
Слайд 3Цель:
Изучить основы гидродинамики.
Получить навыки постановки и решения простейших задач гидродинамики.
Задачи:
Вывод
основных уравнений гидродинамики.
Закономерности изотермических движений жидкости.
Решение задач гидродинамики.
Закономерности изотермических движений жидкости.
Решение задач гидродинамики.
Слайд 4Введение
Гидродинамика – раздел механики сплошных сред, в котором изучается движение несжимаемой
жидкости с дозвуковыми скоростями и ее взаимодействие с твердыми телами.
Термин «жидкость» относится как к капельной жидкости, так и к газу.
Термин «жидкость» относится как к капельной жидкости, так и к газу.
Слайд 5Жидкость называют несжимаемой, если ее плотность одинакова по всему объему жидкости
и в любой точке не изменяется с течением времени:
ρ = const
Это приближение выполняется с высокой точностью для капельных жидкостей ввиду малых изменений плотности при значительных увеличениях давления.
ρ = const
Это приближение выполняется с высокой точностью для капельных жидкостей ввиду малых изменений плотности при значительных увеличениях давления.
Слайд 6Так, например, если воду поместить в цилиндр с подвижным поршнем и
увеличить давление от одной до двух атмосфер, то это уменьшит объем воды только в отношении 1 : 20000.
Такое повышение давления в случае воздуха при неизменной температуре уменьшает объем в отношении 1 : 2 в соответствии с законом Бойля – Мариотта.
Такое повышение давления в случае воздуха при неизменной температуре уменьшает объем в отношении 1 : 2 в соответствии с законом Бойля – Мариотта.
Слайд 7Многочисленные экспериментальные и теоретические исследования показывают, что изменение плотности газа не
существенно при дозвуковых скоростях его движения. Если бы это было не так, то в газе возник бы волновой процесс, выравнивающий плотность газа по всему объему со скоростью звука. Поэтому при движении газа со скоростью много меньшей скорости звука плотность не успевает изменяться.
Слайд 8Свойства жидкости
Давление жидкости – скалярная физическая величина, характеризующая силу, с которой
жидкость действует на единицу поверхности стенки сосуда перпендикулярно к этой поверхности.
Слайд 9Здесь F – сила, с которой жидкость действует на стенку сосуда
площадью S по нормали к ней.
Если сила распределена вдоль поверхности равномерно, то p – давление жидкости.
В противном случае p – среднее давление жидкости на площадку S, а в пределе при стремлении величины S к нулю, - давление в данной точке.
Если сила распределена вдоль поверхности равномерно, то p – давление жидкости.
В противном случае p – среднее давление жидкости на площадку S, а в пределе при стремлении величины S к нулю, - давление в данной точке.
Слайд 10Закон Паскаля:
В любой точке покоящейся жидкости давление изотропно, т.е. по всем
направлениям одинаково.
Единица измерения давления в СИ - Паскаль:
Единица измерения давления в СИ - Паскаль:
Слайд 11Внесистемные единицы:
1 мм рт. ст. (торр) = 133,3 Па
Физическая атмосфера
1 атм
= 760 мм рт. ст. = 1,01 ⋅ 105 Па
Техническая атмосфера
1 ат = 9,81 ⋅ 104 Па
Техническая атмосфера
1 ат = 9,81 ⋅ 104 Па
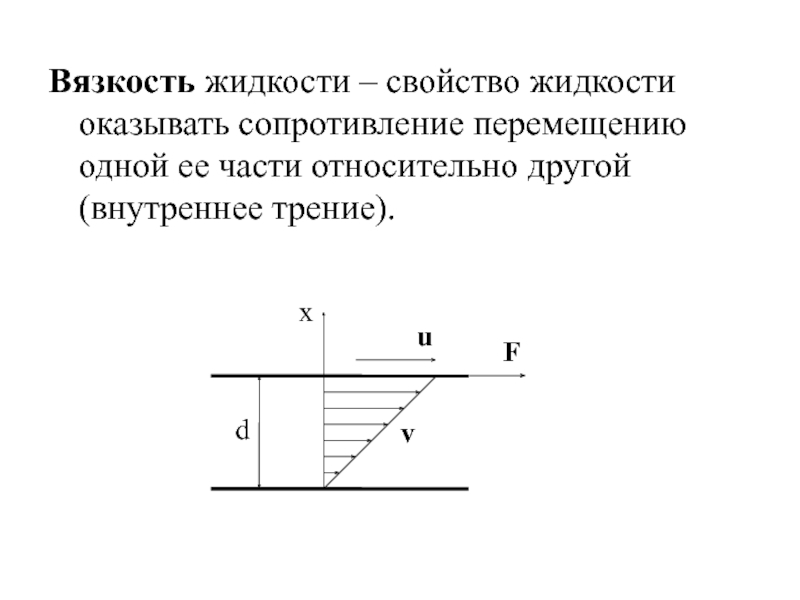
Слайд 12Вязкость жидкости – свойство жидкости оказывать сопротивление перемещению одной ее части
относительно другой (внутреннее трение).
Слайд 13Основной закон вязкого движения жидкости был установлен И. Ньютоном (1687):
F –
тангенциальная сила, вызывающая сдвиг слоев жидкости относительно друг друга; S – площадь слоя, по которому происходит сдвиг; η - коэфф. динамической вязкости (вязкость).
Слайд 16Коэффициент динамической вязкости плотных газов и жидкостей слабо зависит от давления
и сильно – от температуры.
Динамическая вязкость газов при увеличении температуры увеличивается, а жидкостей уменьшается.
Динамическая вязкость газов при увеличении температуры увеличивается, а жидкостей уменьшается.
Слайд 17Уравнение неразрывности
Плотность потока массы – масса жидкости, протекающей за единицу времени
через единичную площадку, перпендикулярную потоку.
Объем:
Масса:
Плотность потока
массы:
Объем:
Масса:
Плотность потока
массы:
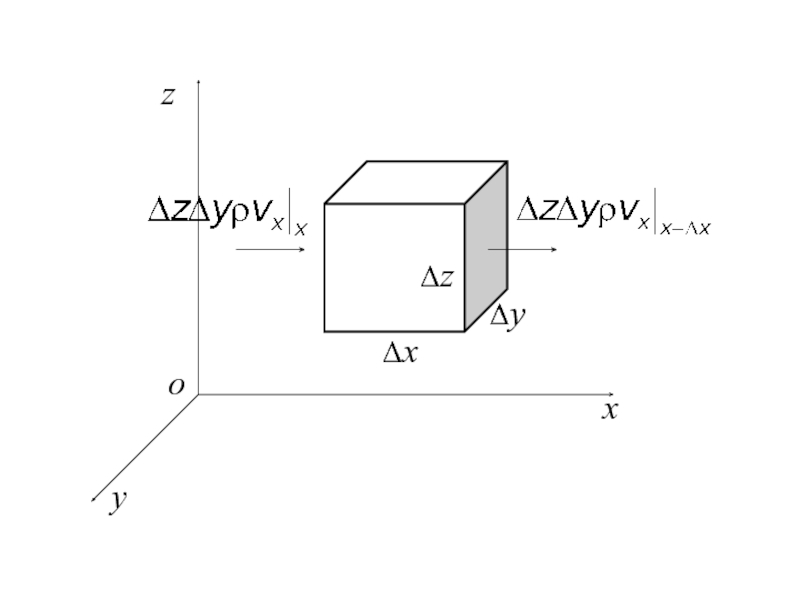
Слайд 18Баланс массы
Мысленно выделим в жидкости фиксированный элемент объема в форме прямоугольного
параллелепипеда, длины ребер которого равны Δx, Δy и Δz.
Вычислим скорость изменения массы жидкости в этом объеме.
Вычислим скорость изменения массы жидкости в этом объеме.
Слайд 20Скорость изменения массы жидкости в объеме за счет потока вдоль оси
x
Аналогично по координатным осям y и z
Аналогично по координатным осям y и z
Слайд 21Скорость накопления массы в выделенном элементе объема равна
Разделим это уравнение на
ΔxΔyΔz и устремим величину элемента объема к нулю.
Слайд 22В результате получим
или
Это уравнение неразрывности. Определяет скорость изменения массы единичного
объема жидкости.
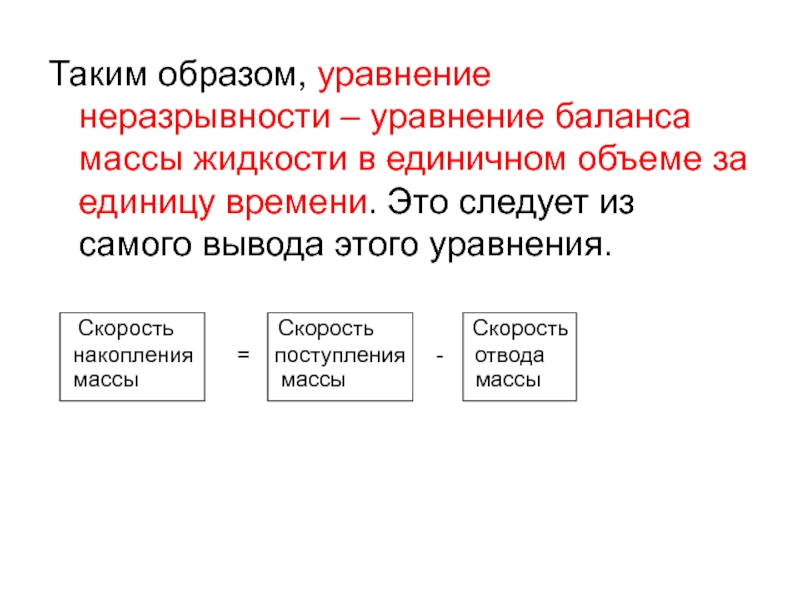
Слайд 23Таким образом, уравнение неразрывности – уравнение баланса массы жидкости в единичном
объеме за единицу времени. Это следует из самого вывода этого уравнения.
Скорость Скорость Скорость
накопления = поступления - отвода
массы массы массы
Скорость Скорость Скорость
накопления = поступления - отвода
массы массы массы