- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Магнитное поле и его характеристики презентация
Содержание
- 1. Магнитное поле и его характеристики
- 2. МАГНИТНОЕ ПОЛЕ МАГНИТНОЕ ПОЛЕ – одна из
- 3. Все постоянные магниты имеют два разноимен-ных полюса:
- 4. Между двумя движущимися друг относительно друга
- 6. Магнитной индукцией В называется векторная физическая
- 7. МАГНИТНЫЙ МОМЕНТ – векторная величина, характеризующая
- 8. СИЛА ЛОРЕНЦА. ЗАКОН АМПЕРА. В общем случае
- 9. Разделение силы Лоренца на электрическую и
- 10. Формула (2.9) выражает закон Ампера: Сила,
- 11. Магнитное поле оказывает ориентирующее действие на
- 12. (2.14) где интегрирование проводится по
- 13. НАПРЯЖЕННОСТЬ МАГНИТНОГО ПОЛЯ Ампер (1775-1836) предположил, что
- 14. Магнитное поле макротоков описывается ВЕКТОРОМ НАПРЯЖЕННОСТИ МАГНИТНОГО
- 15. ЗАКОН БИО – САВАРА – ЛАПЛАСА
- 16. Направление перпендикулярно и ,
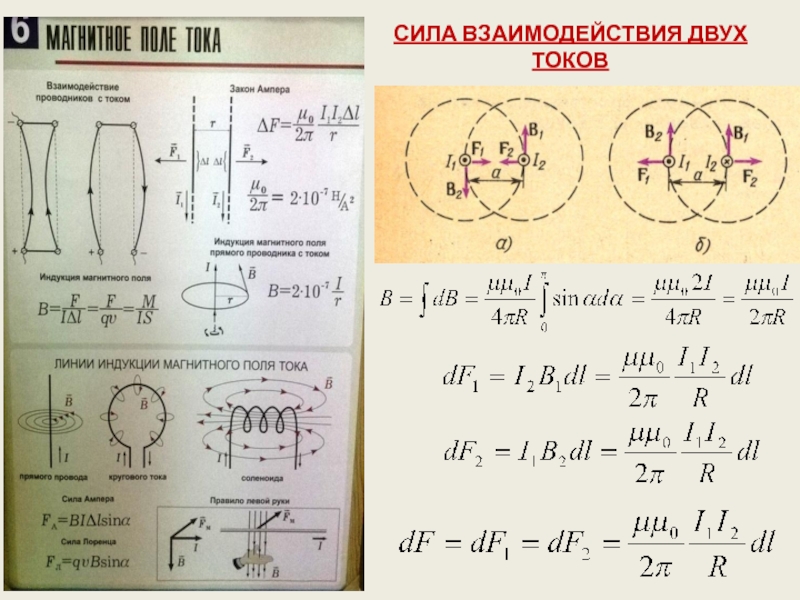
- 19. СИЛА ВЗАИМОДЕЙСТВИЯ ДВУХ ТОКОВ
- 20. МАГНИТНАЯ ПОСТОЯННАЯ. ЕДИНИЦЫ ИЗМЕРЕНИЯМАГНИТНОЙ ИНДУКЦИИ И НАПРЯЖЕННОСТИ
- 21. вакууме на расстоянии 1 м один от
- 22. Единица измерения магнитной индукции – Тл (Тесла).
- 23. МАГНИТНОЕ ПОЛЕ ДВИЖУЩЕГОСЯ ЗАРЯДА
- 24. Каждый проводник с током создает в пространстве
- 25. Формула магнитной индукции свободно двигающегося заряда в
Слайд 2МАГНИТНОЕ ПОЛЕ
МАГНИТНОЕ ПОЛЕ – одна из форм проявления электро-магнитного поля, отличающаяся
МАГНИТНОЕ ПОЛЕ создается проводниками с током, движущимися электрически заряженными частицами и телами с магнитным моментом, отличным от нуля.
Слайд 3Все постоянные магниты имеют два разноимен-ных полюса: северный и южный.
Одноименные полюса
Существует магнитное поле Земли, обусловлен-ное, в основном, процессами происходящими в жидком ядре Земли. Магнитные полюса Земли не совпадают с географическими (северный маг-нитный находится около южного географическо-го), угол между осью вращения Земли и линией соединяющей магнитные полюса 11,5°.
Слайд 4
Между двумя движущимися друг относительно друга заря-женными частицами существуют и электрическое,
Опыты показывают, что сила Fмаг, действующая со стороны магнитного поля на движущуюся в этом поле заряженную частицу, подчиняется следующим закономерностям:
сила Fмаг всегда перпендикулярна вектору скорости υ частицы;
отношение Fмаг/(|q| υ) не зависит ни от заряда q частицы, ни от модуля ее скорости;
при изменении направления скорости частицы модуль силы Fмаг изменяется от 0 до максимального значения (Fм)макс, кото-рое зависит от значения силовой характеристики магнитного поля – вектора В, называемого магнитной индукцией поля.
Для графического изображения стационарного, т. е. не изме-няющегося со временем, магнитного поля пользуются мето-дом линий магнитной индукции (силовых линий магнит. поля).
Слайд 5
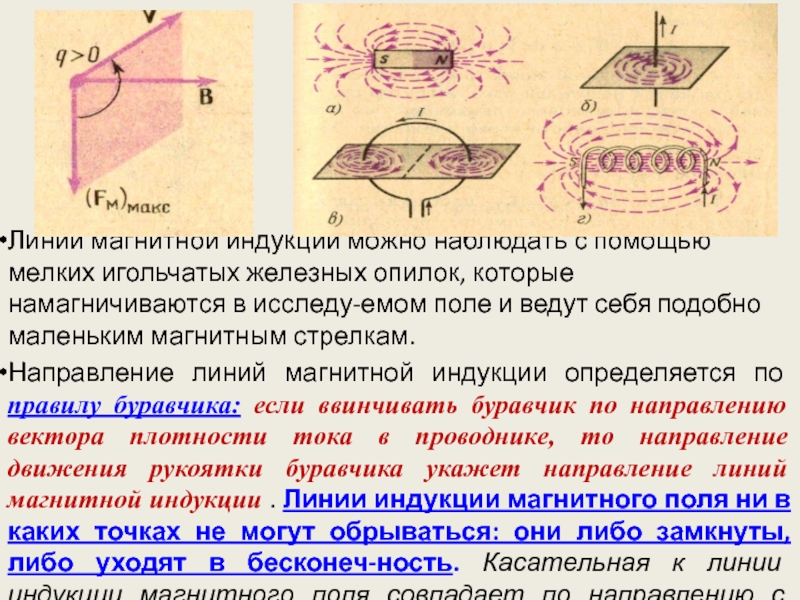
Линии магнитной индукции можно наблюдать с помощью мелких игольчатых железных опилок,
Направление линий магнитной индукции определяется по правилу буравчика: если ввинчивать буравчик по направлению вектора плотности тока в проводнике, то направление движения рукоятки буравчика укажет направление линий магнитной индукции . Линии индукции магнитного поля ни в каких точках не могут обрываться: они либо замкнуты, либо уходят в бесконеч-ность. Касательная к линии индукции магнитного поля совпадает по направлению с вектором магнитной индукции В в этой точке.
Слайд 6
Магнитной индукцией В называется векторная физическая величина численно равная максимальной силе
В= (Fм)макс/(|q| υ) (2.1)
Магнитной индукцией В называется векторная физическая величина численно равная максимальной силе (Fм)макс, дей-ствующей со стороны магнитного поля на проводник единич-ной длины при токе в нем I=1A.
B= (Fм)макс/(I∙l) (2.2)
Магнитной индукцией В называется векторная физическая величина численно равная максимальному вращающему мо-менту (Мм)макс, действующему со стороны магнитного поля на замкнутый контур с током с магнитным моментом рm=1 А∙м2.
B= (Мм)макс/рm (2.4)
Слайд 7
МАГНИТНЫЙ МОМЕНТ – векторная величина, характеризующая магнитные свойства тел и частиц
нию силы тока на площадь , ограниченную контуром, и направленная перпендикулярно к плоскости контура, в соответствии с правилом правого винта. – единич-ный вектор нормали к площади контура.
(2.5)
Магнитное поле оказывает на рамку с током ориентиру-ющее воздействие, поворачивая её так, чтобы направ-ление вектора совпало с направлением вектора магнитной индукции В, т. е. плоский замкнутый контур с током ведет себя в магнитном поле также, как и маг-нитная стрелка.
Слайд 8СИЛА ЛОРЕНЦА. ЗАКОН АМПЕРА.
В общем случае сила, действующая со стороны магнитного
(2.6)
(2.7)
где α- угол между векторами и .
Сила направлена перпендикулярно скорости заряженной частицы и сообщает частице только нормальное ускорение. Эта сила не совершает работы и вызывает лишь искривление траектории частицы. Поэтому при движении свободной заря-женной частицы в магнитном поле ее кинетическая энергия не изменяется.
(2.8)
Слайд 9
Разделение силы Лоренца на электрическую и магнитную составляющие относительно, т. е.
На проводники с электрическим током, находящиеся в магнитном поле, действуют силы Ампера.
Сила Ампера dF, приложенная к малому элементу провод-ника с током I, равна геометрической сумме сил, которые действуют со стороны магнитного поля на движущиеся в про-воднике носители тока.
(2.9)
Слайд 10
Формула (2.9) выражает закон Ампера:
Сила, действующая на элемент проводника с током
Сила Ампера, действующая в магнитном поле на проводник конечной длины l с током I , равна геометрической сумме сил Ампера, действующих на все малые элементы этого проводника: (2.11)
Слайд 11
Магнитное поле оказывает ориентирующее действие на зам-кнутый проводящий контур, по которому
Результирующий вращающий момент М, действующий на рамку (контур) с током, равен моменту пары сил:
М=I∙a∙b∙B∙sinβ =I∙S∙B∙sinβ =pm∙B∙sinβ . (2.12)
(2.13)
Если контур с током находится в неоднородном магнитном поле, то действие сил Ампера на контур не сводится только к результирующему вращающему моменту (2.13). В этом случае на контур действует еще и результирующая сила:
Слайд 12
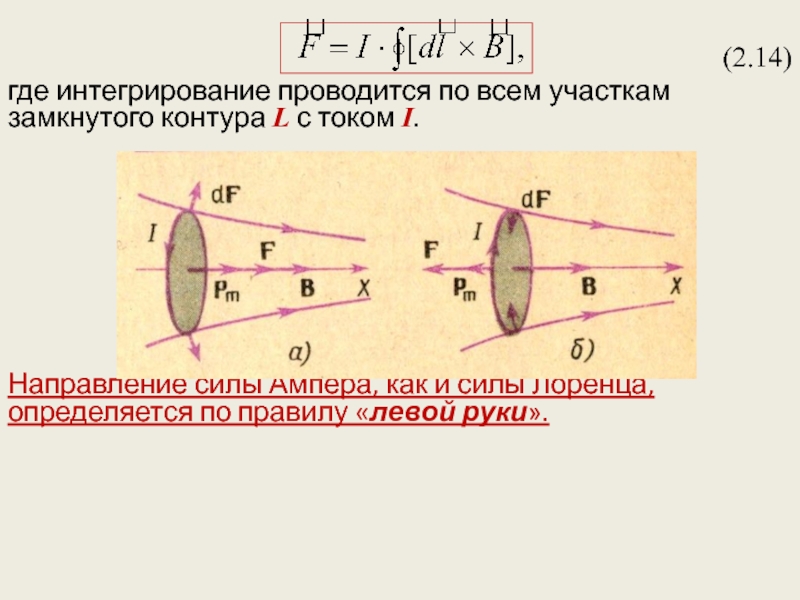
(2.14)
где интегрирование проводится по всем участкам замкнутого контура L с током
Направление силы Ампера, как и силы Лоренца, определяется по правилу «левой руки».
Слайд 13НАПРЯЖЕННОСТЬ МАГНИТНОГО ПОЛЯ
Ампер (1775-1836) предположил, что в любом теле су-ществуют микроскопические
Если вблизи тела поместить проводник с током (макро-ток), то под действием его магнитного поля, микротоки во всех атомах определенным образом ориентируются, создавая в теле дополнительное магнитное поле. Маг-нитная индукция характеризует результирующее маг-нитное поле, создаваемое всеми макро- и микротоками. То есть: при одном и том же токе и равных условиях,в различных средах значения вектора магнитной индук-ции будут иметь различные значения.
Слайд 14Магнитное поле макротоков описывается ВЕКТОРОМ НАПРЯЖЕННОСТИ МАГНИТНОГО ПОЛЯ .
(2.15)
– магнитная постоянная.
– магнитная проницаемость среды, показывающая во сколько раз магнитное поле макротоков усилива-ется за счет магнитного поля микротоков среды.
Сравнивая векторные характеристики электростатическо-кого и магнитного полей, можно заметить что аналогом вектора электрического смещения явля-ется вектор напряженности магнитного поля , а ана-логом вектора напряженности электрического поля , является вектор магнитной индукции .
Слайд 15ЗАКОН БИО – САВАРА – ЛАПЛАСА
Магнитное поле постоянного тока изу-чалось
Для проводника с током I, элемент которого dl создает в не-которой точке C магнитное поле с индукцией dB, было полу-чено соотношение:
(2.16)
– вектор равный по модулю длине проводника dl и сов-падающий по направлению с током I, – радиус-вектор, проведенный из элемента проводника dl в точку C поля.
Слайд 16Направление перпендикулярно и , то есть перпенди-кулярно плоскости,
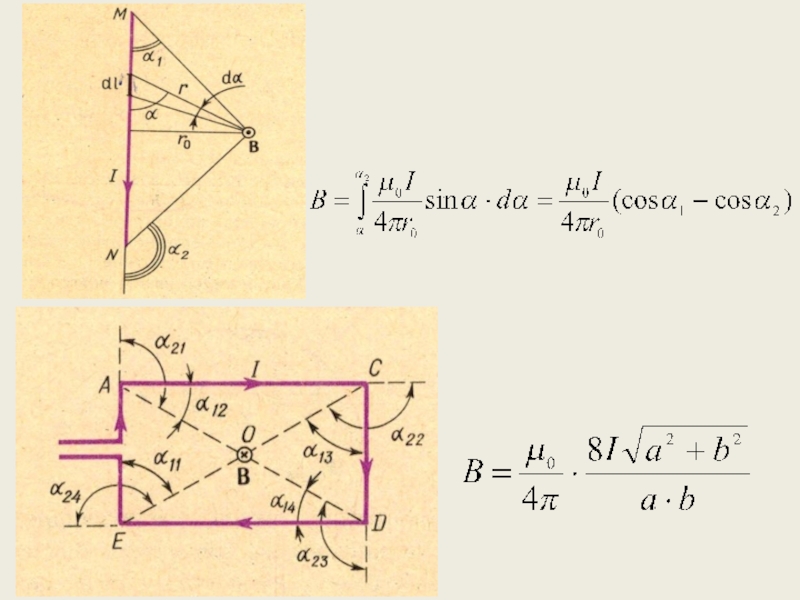
Закон Био – Савара – Лапласа в скалярной форме
(2.17)
– угол между векторами и .
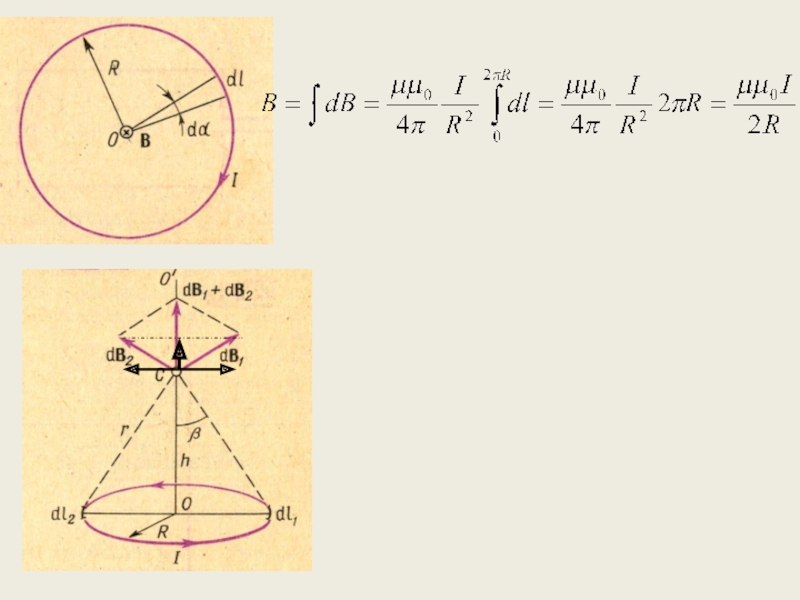
Для магнитного как и для электрического полей справедлив ПРИНЦИП СУПЕРПОЗИЦИИ: Магнитная индукция, создавае-мая в одной точке несколькими движущимися зарядами или токами, равна векторной сумме магнитных индукций, созда-ваемых каждым током (зарядом) в отдельности.
Слайд 20МАГНИТНАЯ ПОСТОЯННАЯ. ЕДИНИЦЫ ИЗМЕРЕНИЯМАГНИТНОЙ ИНДУКЦИИ И НАПРЯЖЕННОСТИ МАГНИТНОГО ПОЛЯ
Если два параллельных
Для определения численного значения магнитной пос-тоянной , воспользуемся определением ампера (единицы измерения силы тока), согласно которому: АМПЕР- сила неизменяющегося тока, который при прохождении по двум параллельным прямолиней-ным проводникам бесконечной длины и ничтожно малого поперечного сечения, расположенного в
Слайд 21 вакууме на расстоянии 1 м один от другого, создаёт между проводниками
Следовательно, если и то
Где Гн (генри) единица индуктивности (НЕ ИНДУКЦИИ!!)
Слайд 22Единица измерения магнитной индукции – Тл (Тесла).
1 Тл – магнитная индукция
Единица измерения напряженности магнитного поля – А/м (ампер/метр).
1 А/м – напряженность такого поля, магнитная индук-ция которого в вакууме 4π·10¯⁷ Тл.
Слайд 24Каждый проводник с током создает в пространстве маг-нитное поле. Ток –
Свободно двигающийся заряд ( заряд двигающийся с постоянной нерелятивистской скоростью ), создает в точке М, на расстоянии магнитное поле с индукцией .
Вектор направлен перпендикулярно плоскости
в которой расположены и . Его направление – по-ступательное движение правого винта, при его вращении от к .
Слайд 25Формула магнитной индукции свободно двигающегося заряда в скалярной форме:
Движущийся заряд по
Эти закономерности справедливы только при малых скоростях движущегося заряда, когда электрическое поле свободно двигающегося заряда можно считать электростатическим , то есть неподвижным зарядом в той точке в которой находится двигающийся заряд.