Принцип Гюйгенса-Кирхгофа.
Излучатель Гюйгенса.
Принцип получения остронаправленного излучения.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция №6 (6 ). Поле системы элементарных излучателей презентация
Содержание
- 1. Лекция №6 (6 ). Поле системы элементарных излучателей
- 2. Электродинамика и РРВ.Сем.1. Лекция 6(6). 1 Принцип
- 3. Электродинамика и РРВ.Сем.1. Лекция 6(6). Введение эквивалентных
- 4. Электродинамика и РРВ.Сем.1. Лекция 6(6). Принцип Гюйгенса-Кирхгофа:
- 5. Электродинамика и РРВ.Сем.1. Лекция 6(6). Фронт волны
- 6. Электродинамика и РРВ.Сем.1. Лекция 6(6). 2 Излучатель
- 7. Электродинамика и РРВ.Сем.1. Лекция 6(6). Элемент Гюйгенса
- 8. Электродинамика и РРВ.Сем.1. Лекция 6(6). 3 Принцип
- 9. Электродинамика и РРВ.Сем.1. Лекция 6(6). Преобразование
- 10. Электродинамика и РРВ.Сем.1. Лекция 6(6). 2. Представим
- 11. Электродинамика и РРВ.Сем.1. Лекция 6(6). Анализ характеристики
- 12. Электродинамика и РРВ.Сем.1. Лекция 6(6). График
- 13. Ширина ДН в зависимости от размера отверстия
Слайд 1Электродинамика и РРВ.Сем.1. Лекция 6(6).
Тема 2. ИЗЛУЧЕНИЕ ЭМВ
В СВОБОДНОЕ ПРОСТРАНСТВО
Лекция
Слайд 2Электродинамика и РРВ.Сем.1. Лекция 6(6).
1 Принцип Гюйгенса-Кирхгофа
В случаях, когда распределение токов
Реальные источники тока заменяются на эквивалентные,
расположенные не внутри объема, а на его поверхности.
Слайд 3Электродинамика и РРВ.Сем.1. Лекция 6(6).
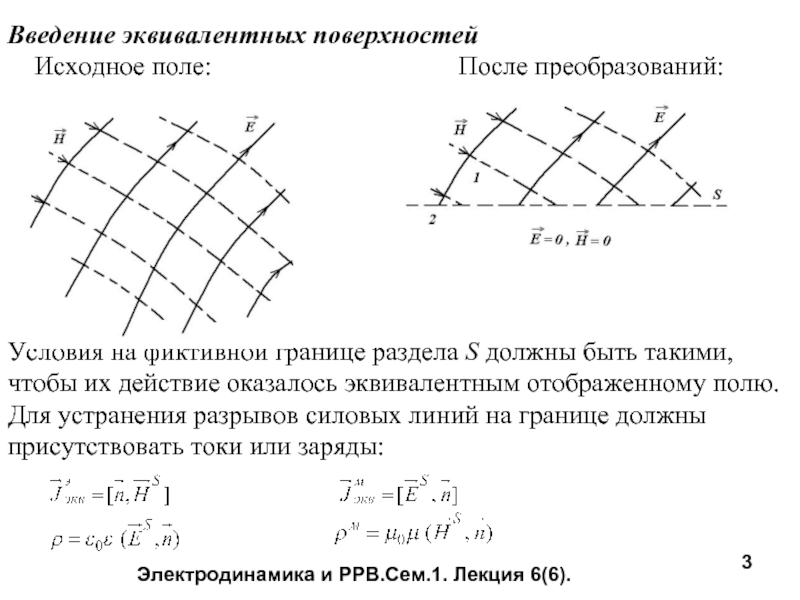
Введение эквивалентных поверхностей
Исходное поле:
Условия на фиктивной границе раздела S должны быть такими, чтобы их действие оказалось эквивалентным отображенному полю. Для устранения разрывов силовых линий на границе должны присутствовать токи или заряды:
Слайд 4Электродинамика и РРВ.Сем.1. Лекция 6(6).
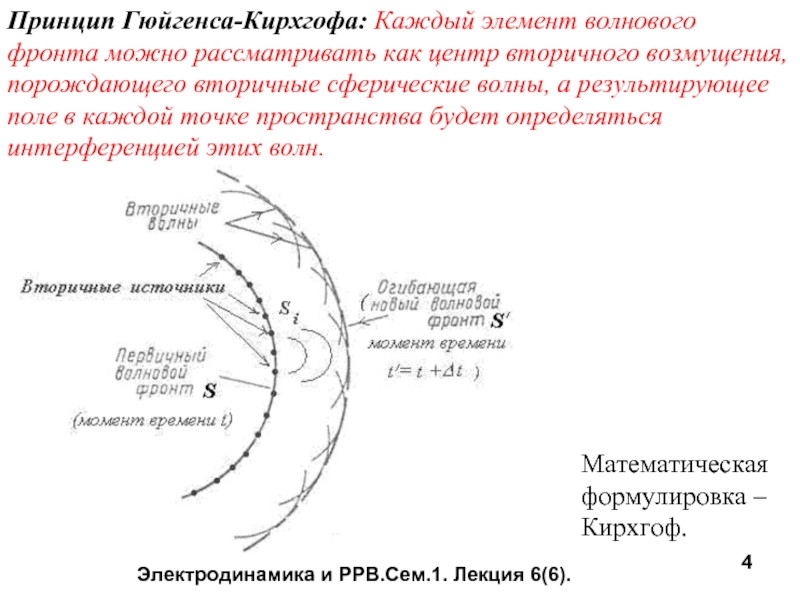
Принцип Гюйгенса-Кирхгофа: Каждый элемент волнового фронта можно
Математическая
формулировка –
Кирхгоф.
Слайд 5Электродинамика и РРВ.Сем.1. Лекция 6(6).
Фронт волны - поверхность, отделяющую область, в
В случае монохроматических ЭМВ, распространяющихся в неограниченной области, под фронтом волны понимают любую поверхность равных фаз.
Результат использования принципа Гюйгенса- Кирхгофа:
Поле в объеме можно рассматривать не только как результат излучения реальных сторонних источников (электрических токов и зарядов), но и как результат излучения эквивалентных источников, распределенных на некоторой поверхности. При этом для определения источников достаточно знать поле на поверхности.
Слайд 6Электродинамика и РРВ.Сем.1. Лекция 6(6).
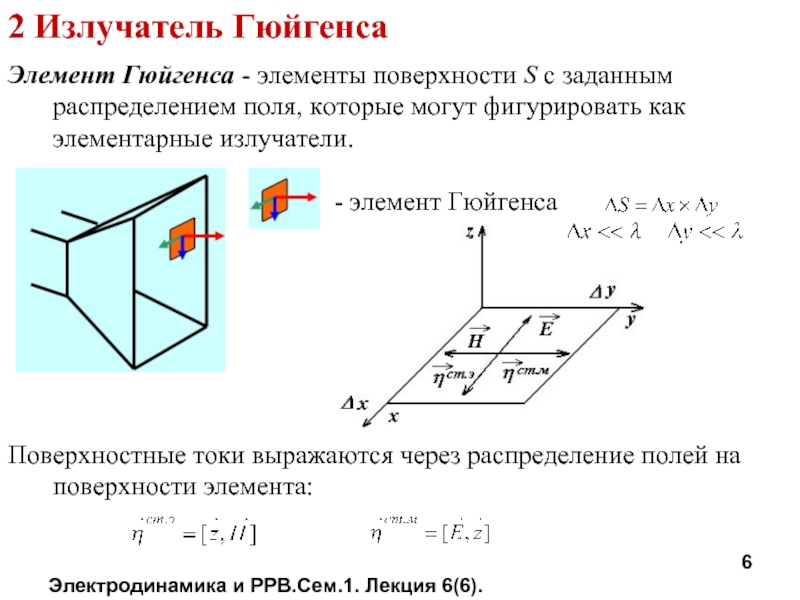
2 Излучатель Гюйгенса
Элемент Гюйгенса - элементы поверхности
- элемент Гюйгенса
Поверхностные токи выражаются через распределение полей на поверхности элемента:
Слайд 7Электродинамика и РРВ.Сем.1. Лекция 6(6).
Элемент Гюйгенса – комбинированный излучатель, составленный из
Поле в дальней
зоне:
Анализ структуры поля в дальней зоне:
Структура поля отличается от структуры полей элементарных излучателей, на основе которых данный элемент образован: имеет две компоненты, а не одну.
Характеристика направленности является векторной величиной
3. Вектор Пойнтинга
Слайд 8Электродинамика и РРВ.Сем.1. Лекция 6(6).
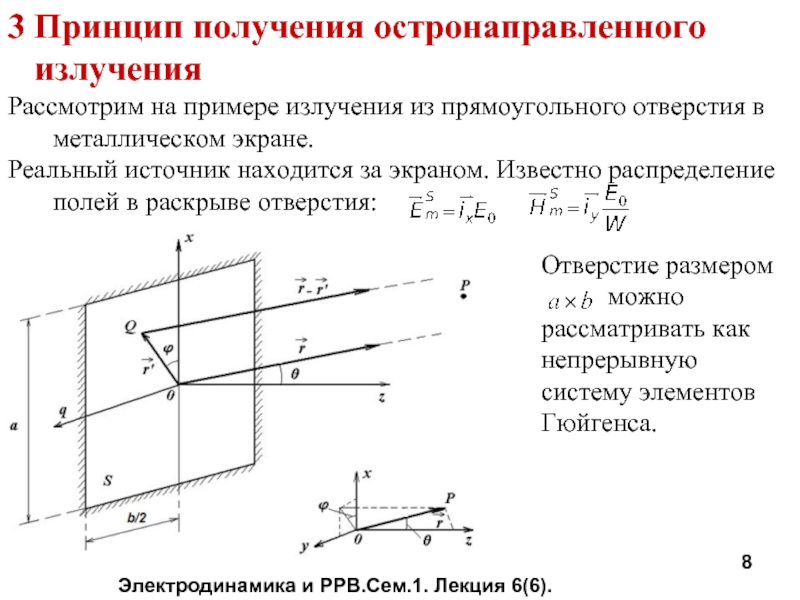
3 Принцип получения остронаправленного
излучения
Рассмотрим на
Реальный источник находится за экраном. Известно распределение полей в раскрыве отверстия:
Отверстие размером
можно
рассматривать как
непрерывную
систему элементов
Гюйгенса.
Слайд 9Электродинамика и РРВ.Сем.1. Лекция 6(6).
Преобразование выражение для компоненты поля в
Отнесем точку наблюдения на бесконечность. Отсюда следует,
- векторы и могут считаться параллельными;
- все точки поверхности S имеют одинаковые угловые
координаты θ′=θ и ϕ′=ϕ;
- множитель можно заменить на ;
- множитель описывает фазу и пока не преобразуется.
В итоге имеем:
Слайд 10Электродинамика и РРВ.Сем.1. Лекция 6(6).
2. Представим выражение
3. Подставим полученное выражение в множитель :
В итоге преобразований получаем:
Слайд 11Электродинамика и РРВ.Сем.1. Лекция 6(6).
Анализ характеристики направленности:
где
При a>>λ и b>>λ интерференционный множитель фактически определяет характеристику направленности в области малых θ.
Е-плоскость (плоскость ориентации вектора ): ϕ=0
Н-плоскость (плоскость ориентации вектора ): ϕ=π/2
где , .
Слайд 12Электродинамика и РРВ.Сем.1. Лекция 6(6).
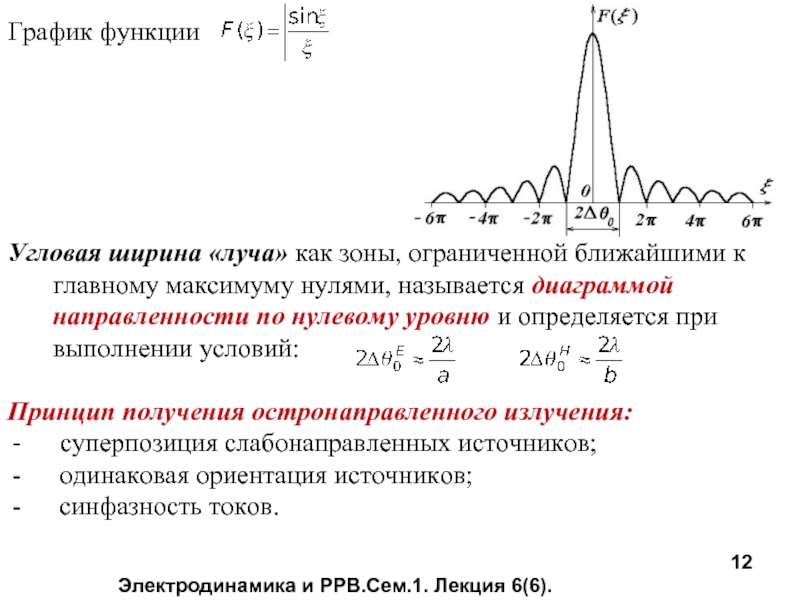
График функции
Угловая ширина «луча» как зоны, ограниченной
Принцип получения остронаправленного излучения:
суперпозиция слабонаправленных источников;
одинаковая ориентация источников;
синфазность токов.
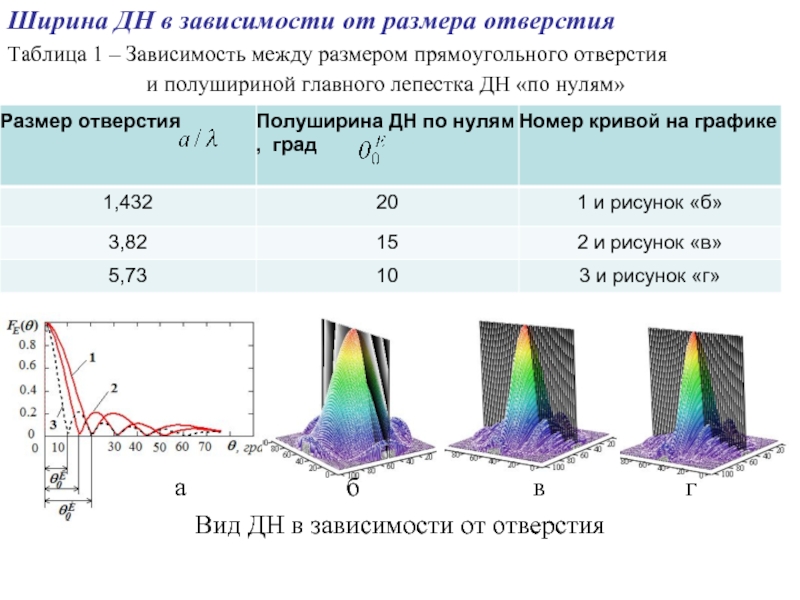
Слайд 13Ширина ДН в зависимости от размера отверстия
Таблица 1 – Зависимость между
и полушириной главного лепестка ДН «по нулям»
а б в г
Вид ДН в зависимости от отверстия