- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 9. Мезонные теории ядерных сил презентация
Содержание
- 1. Лекция 9. Мезонные теории ядерных сил
- 2. Исторический экскурс В 1932-33 гг., сразу после
- 3. Затем Ферми (в 1933 г.), а также
- 4. Тогда Хидеки Юкава (в 1935 г.) предположил,
- 6. Получим теперь выражение для такого обменного взаимодействия.
- 7. Тогда из уравнений Максвелла следуют волновые уравнения
- 8. Запишем теперь Лапласиан в сферических
- 9. Теперь поместим в это мезонное поле второй
- 10. Теперь возникает важный вопрос: Как физически
- 11. Как примирить реальную ситуацию с нашими интуитивными
- 12. Пусть теперь рождаются сразу n мезонов! Тогда
- 13. На самом деле пион — не скаляр,
- 14. Это приводит к тому, что потенциал взаимодействия
- 15. И тогда появляется новая сила взаимодействия, тесно
- 16. Если два нуклона в дейтроне с Jπ = 1+
- 17. Тогда как экспериментальное значение
- 18. Построение феноменологических
- 19. Если теперь частица находится в центрально-симметричном поле
- 20. Для притягивающих потенциалов без связанных состояний:
- 21. Каковы NN-фазовые сдвиги на самом деле? Чтобы
- 22. В итоге, современные NN-потенциалы включают в себя
- 24. Современное развитие Юкавской модели ядерных сил Пошло
- 25. Имеется также более старый и менее точный
- 26. ii. Эффективная теория поля для NN-взаимодействий
- 27. NN-потенциал, построенный в NNLO с
- 28. ВЫВОДЫ Хотя современная картина мезонных обменов в
Слайд 2Исторический экскурс
В 1932-33 гг., сразу после открытия (Чедвиком) нейтрона, Иваненко и
А поскольку уже было известно, что существуют разные изотопы одного и того же элемента, например, 12C, 13C, 14C и т.д., то Гайзенберг предположил, что нейтрон и протон – это фактически одна и та же частица – нуклон, которая находится в разных зарядовых состояниях. На современном языке – это нуклон с разными проекциями изоспина tN=1/2, т.е. находящийся просто в двух разных состояниях!
Далее Гайзенберг предположил, что нуклоны в ядре держатся за счет “обмена местами” (нем. “Platzwechsel”).
Например, в дейтроне:
Слайд 3Затем Ферми (в 1933 г.), а также Тамм и Иваненко
Однако такая сила (слабого взаимодействия) оказалась очень слабой и неспособной связать нуклоны в ядрах.
ν
e-
Гипотеза
np-взаимодействия
Ферми
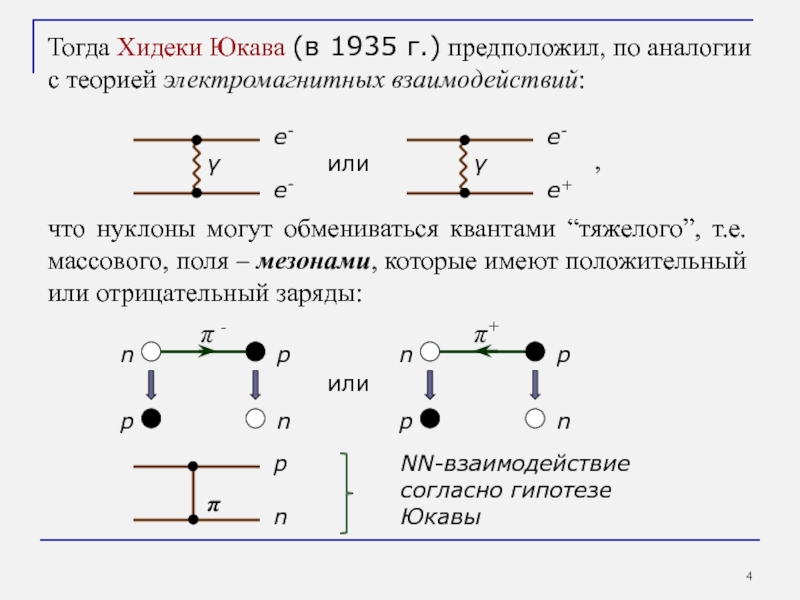
Слайд 4Тогда Хидеки Юкава (в 1935 г.) предположил, по аналогии с теорией
что нуклоны могут обмениваться квантами “тяжелого”, т.е. массового, поля – мезонами, которые имеют положительный или отрицательный заряды:
или
,
Слайд 6Получим теперь выражение для такого обменного взаимодействия.
π-мезон будем считать квантом скалярного
Если в релятивистском соотношении для энергии соотнести: и , как обычно в квантовой механике, то получается уравнение Клейна-Гордона:
При μ = 0 получаем обычное волновое уравнение для безмассового фотона. Такое уравнение описывает распространение электромагнитной волны в пустоте, т.е. там, где нет зарядов – источников электромагнитного поля.
Слайд 7Тогда из уравнений Максвелла следуют волновые уравнения для Φ и
ρ – плотность заряда,
– плотность тока источников поля.
Слайд 8Запишем теперь Лапласиан в сферических координатах:
– оператор
Слайд 9Теперь поместим в это мезонное поле второй нуклон с таким же
Ясно, что потенциальная энергия второго нуклона в этом поле будет:
(Например, в электромагнетизме потенциальная энергия электрического заряда e в скалярном поле Φ есть U=eΦ, и у нас играет роль Φ, ибо уравнения для них одинаковы.)
Впоследствии (в 1947 г.) эти (псевдо)скалярные частицы, предсказанные Юкавой, были открыты в космических лучах, и их масса оказалась на самом деле около 140 МэВ.
Слайд 10Теперь возникает важный вопрос:
Как физически понять такой обменный механизм взаимодействия
Если протон испускает (реально) π-мезон с массой mπ, то кажется, что его масса должна уменьшиться на эту массу mπ. Тогда протон должен превратиться совсем в другую частицу! И обратно: если нейтрон поглощает такой мезон, то его масса должна увеличиться на 140 МэВ, и он тогда должен превратиться совсем в другую частицу?
Но в реальности протон, испуская π-мезон, превращается в нейтрон почти такой же массы, и наоборот: нейтрон, поглощая π-мезон, превращается в протон.
n
p
mN ≈ 940 МэВ
π
π
mπ ≈ 140 МэВ
Виртуальные и реальные частицы:
в чем разница?
Слайд 11Как примирить реальную ситуацию с нашими интуитивными ожиданиями?
Для этого вспомним
Он означает, что на очень короткое время Δt можно родить или поглотить частицу с массой Δm ≈ ΔE/c2. Отсюда следует, что у взаимодействия, связанного с обменом частицей массы m, радиус действия должен быть порядка комптоновской длины волны λC = ћ/mc.
Откуда это следует?
Если рождается промежуточная частица массы m, то неопределенность в энергии должна быть mc2, и поэтому длительность существования такой частицы будет Δt ≈ ћ/ΔE = ћ/mc2, а путь, который частица может пройти, есть l = c·Δt ≈ ћ/mc = λC.
Т.е. рождение и поглощение пионов нуклонами не нарушает никаких законов сохранения (энергии–импульса), т.к. находится в согласии с соотношением неопределенностей для энергии–времени.
Слайд 12Пусть теперь рождаются сразу n мезонов!
Тогда энергии промежуточных состояний равны n·mc2,
Т.е. взаимодействие, отвечающее обмену одним пионом (n = 1), имеет самый большой радиус и называется
OPEP (One-Pion-Exchange-Potential).
Радиус двухпионного обмена
будет в два раза меньше (т.е. ~ 0.7 Фм) и т.д.
Слайд 13На самом деле пион — не скаляр, а псевдоскаляр, т.к. его
Кроме того, было экспериментально найдено, что имеются три разных пиона: два заряженных π + и π - и один нейтральный π 0.
Т.е. эти три пиона соответствуют изотопическому спину I = 1, имеющему три проекции I+1 = +1, I0 = 0, I-1 = -1, отвечающие как раз трем разным пионам. Т.е. пион — это изовектор (вектор в изотопическом пространстве).
Псевдоскалярная природа пиона
и πN-связи
Слайд 14Это приводит к тому, что потенциал взаимодействия пиона и нуклона включает
И тогда правильный юкавский потенциал равен:
спин-изоспиновый фактор
безразмерная
Но и это еще не всё.
Благодаря присутствию оператора спин нуклона при излучении пиона (в P‑волне) переворачивается.
Переворачивается и спин нуклона при поглощении пиона.
Слайд 15И тогда появляется новая сила взаимодействия, тесно связанная со спином двунуклонной
Именно, если общий спин двух нуклонов SNN = 1, то при фиксированном полном моменте возможны два значения L. Например, для дейтрона J = 1, S = 1 L = J ± 1 = .
0 – S-волна
2 – D-волна
Слайд 16Если два нуклона в дейтроне с Jπ = 1+ находятся в S-состоянии относительного
дейтрон должен обладать полностью аддитивным магнитным
моментом:
μd = μp + μn, т.е. μd = (2.7927 – 1.9135) μN = 0.8792 μN
(μN – ядерный магнетон).
(такие обменные токи дают малый вклад в зарядовую плотность в дейтроне)
Экспериментальные доказательства существования тензорного NN-потенциала в дейтроне
Слайд 17Тогда как экспериментальное значение
С другой стороны, экспериментально известно (с 1939 г.), что дейтрон обладает квадрупольным моментом Qd ≠ 0 (Qd = +2.74·10-27 см2), что возможно только, если в дейтроне есть D-волна (L = 2).
Слайд 18Построение феноменологических NN-потенциалов, подгонка под
Понятие о парциальных фазовых сдвигах рассеяния
(см. учебники по квантовой механике)
Рассмотрим сначала свободное движение бесспиновой частицы в сферической системе координат. Тогда угловой момент и его проекция являются хорошими квантовыми числами решение УШ для свободной частицы можно разложить по базису сферических гармоник Ylm(θ,φ).
Тогда, отделяя угловые переменные в УШ, получим радиальное уравнение:
Это уравнение Бесселя. При E > 0 уравнение имеет одно физически приемлемое решение: jl(ρ) – функция Бесселя.
Тогда:
На асимптотике:
обезразм. энергия
где
Слайд 19Если теперь частица находится в центрально-симметричном поле V(r), то УШ имеет
В асимптотической области V(r) → 0 для короткодействующего потенциала V(r). Тогда в асимптотической области r → ∞ снова приходим к свободному УШ, решения которого имеют вид:
Это решение можно переписать в виде:
Т.е. получается, что вся информация о взаимодействии частиц “сидит” в фазовых сдвигах δl(E). Тогда разные модели потенциалов взаимодействия приводят к разным значениям и разному поведению с энергией для фазовых сдвигов δl(E).
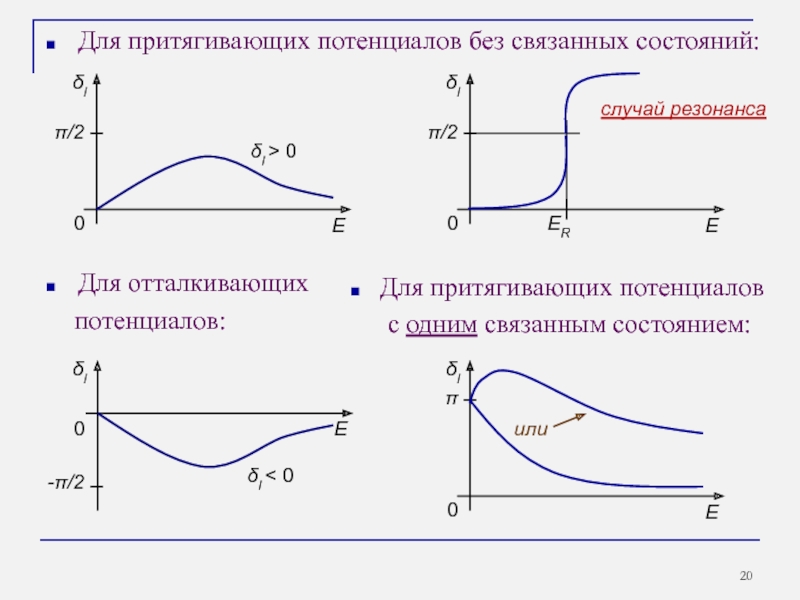
Слайд 20Для притягивающих потенциалов без связанных состояний:
Для отталкивающих
потенциалов:
случай резонанса
0
с одним связанным состоянием:
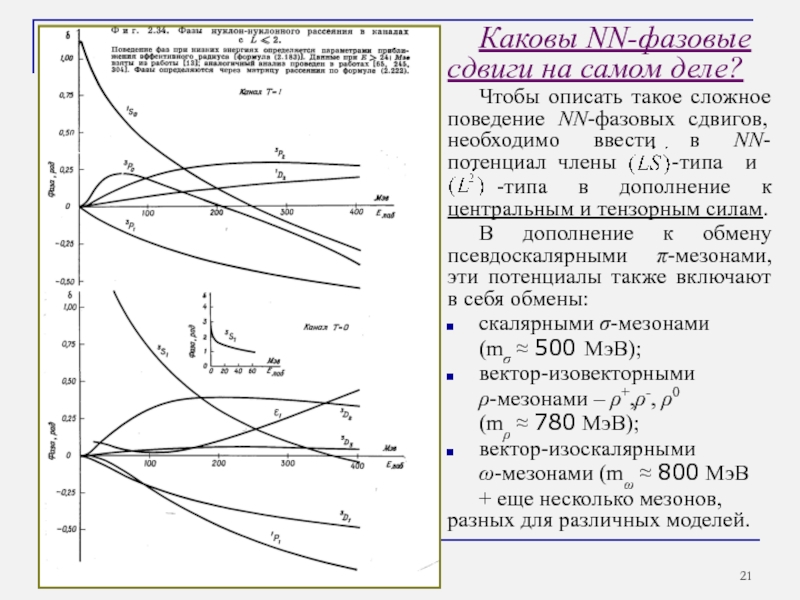
Слайд 21Каковы NN-фазовые сдвиги на самом деле?
Чтобы описать такое сложное поведение NN-фазовых
-типа в дополнение к центральным и тензорным силам.
В дополнение к обмену псевдоскалярными π-мезонами, эти потенциалы также включают в себя обмены:
скалярными σ-мезонами
(mσ ≈ 500 МэВ);
вектор-изовекторными
ρ-мезонами – ρ+,ρ-, ρ0
(mρ ≈ 780 МэВ);
вектор-изоскалярными
ω-мезонами (mω ≈ 800 МэВ
+ еще несколько мезонов, разных для различных моделей.
Слайд 22В итоге, современные NN-потенциалы включают в себя члены типа:
При этом радиальные
Таким образом, современные феноменологические NN-потенциалы включают в себя 40-45 подгоночных параметров, но зато позволяют хорошо описать 2000-3000 (!) экспериментальных точек, отвечающих сечениям NN-рассеяния и разным спиновым наблюдаемым.
где
Слайд 23
Все вышесказанное составляет в первом приближении современный NN-потенциал!
Он хорошо описывает
Слайд 24Современное развитие Юкавской модели ядерных сил
Пошло по двум основным направлениям:
Построение феноменологических
Развитие эффективной теории поля — effective field theory (EFT) — для NN-взаимодействий (1990–2005 гг.)
i. Сейчас известны 4 таких NN-модели высокой точности:
i-1. Аргоннский NN-потенциал
[R.B. Wiringa, V.G.J. Stocks, R. Schiavilla, Phys. Rev. C 51, 38 (1995)]
i-2. Боннский NN-потенциал; последняя версия – CD-Bonn
[R. Machleidt, Phys. Rev. C 63, 024001 (2001)]
i-3. Наймегенский NN-потенциал
[V.G.J. Stocks et al., Phys. Rev. C 49, 2950 (1994)]
i-4. Улучшенный NN-потенциал Рейда (Reid93) [см. i-3.]
Слайд 25Имеется также более старый и менее точный
Парижский
[M. Lacombe et al., Phys. Rev. C 21, 861 (1980)].
Все эти потенциалы подогнаны под NN-наблюдаемые (прямо под измерения) вплоть до энергий EN = 350 МэВ (в л.с.) и с χ2≈1.
Имеется еще нетрадиционный Московский NN-потенциал, предложенный в середине 80-х гг. и полностью построенный для всех парциальных волн в 1998 г.
Но он уже более тесно связан с кварковой моделью, чем с классической картиной мезонного обмена Юкавы.
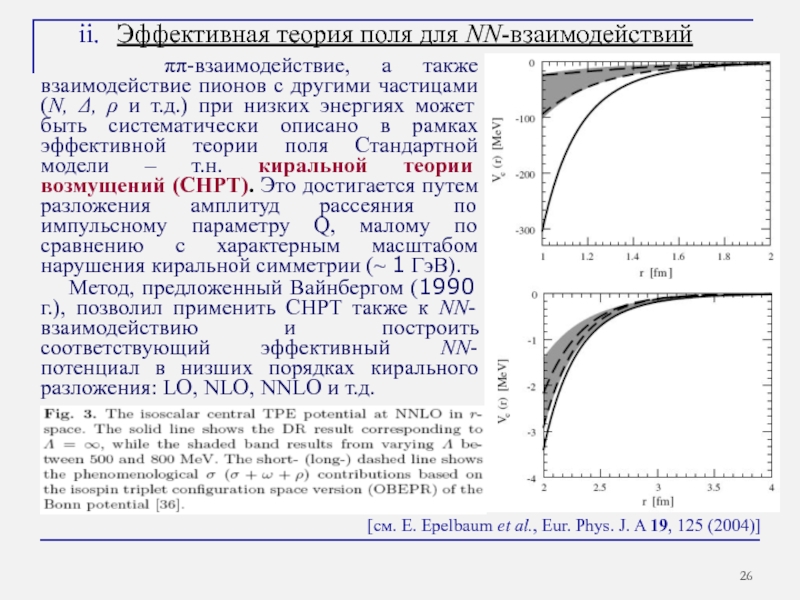
Слайд 26ii. Эффективная теория поля для NN-взаимодействий
[см. E. Epelbaum et al., Eur. Phys. J. A 19, 125 (2004)]
ππ-взаимодействие, а также взаимодействие пионов с другими частицами (N, Δ, ρ и т.д.) при низких энергиях может быть систематически описано в рамках эффективной теории поля Стандартной модели – т.н. киральной теории возмущений (CHPT). Это достигается путем разложения амплитуд рассеяния по импульсному параметру Q, малому по сравнению с характерным масштабом нарушения киральной симметрии (~ 1 ГэВ).
Метод, предложенный Вайнбергом (1990 г.), позволил применить CHPT также к NN-взаимодействию и построить соответствующий эффективный NN-потенциал в низших порядках кирального разложения: LO, NLO, NNLO и т.д.
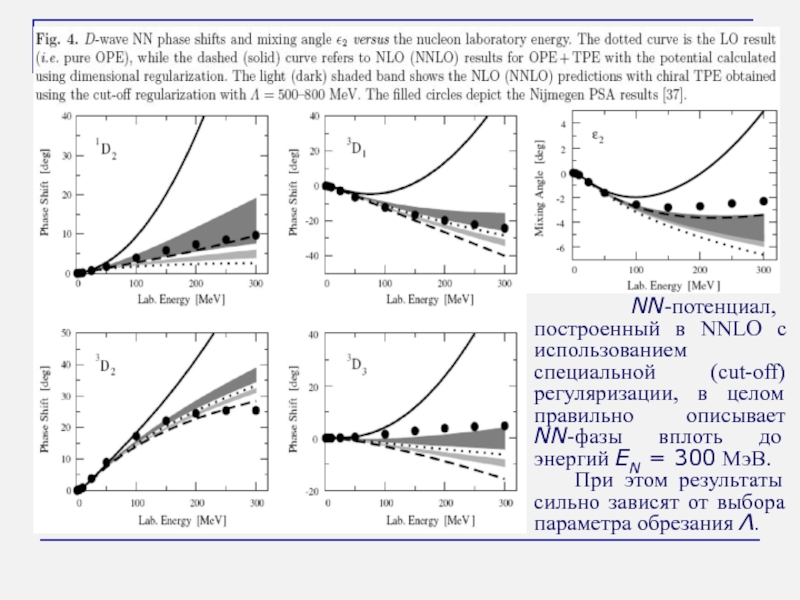
Слайд 27 NN-потенциал, построенный в NNLO с использованием специальной (cut-off) регуляризации,
При этом результаты сильно зависят от выбора параметра обрезания Λ.