- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Електростатика. Закон взаємодії електричних зарядів презентация
Содержание
- 1. Електростатика. Закон взаємодії електричних зарядів
- 2. Зміст 2.1. Закон взаємодії електричних зарядів 2.2.
- 3. Із повсякденної практики
- 4. 2.2 Основні характеристики електричного поля 2.2. Основні
- 5. Напруженість електричного поля залежить від
- 6. Для однорідного лінійного ізотропного середовища (середовища,
- 7. Визначимо вектор електричного зміщення із
- 8. Параметр характеризує діелектричне середовище.
- 9. Для монохромного поля та однорідного нелінійного
- 10. Нехай маємо поле точкового заряду,
- 11. 2.3 Закон
- 12. Нехай вектор , який створено зарядом ,
- 13. Закон Гаусса в інтегральній формі свідчить, що
- 14. 2.3.2. Закон Гауса в диференціальній формі Рисунок
- 15. Визначимо будь-яку точку (x,y,z) у просторі, в
- 16. Оскільки елемент поверхні дуже малий, значення модуля
- 17. Додамо інтеграли (1234) та (5678), й отримаємо:
- 18. Таким чином, застосовано закон Гауса для обмеженого
- 19. Якщо врахувати, що потоку можна приписати алгебраїчний
- 20. . 2.3.3
- 21. Рисунок 2.7 –
- 22. .
- 23. 2.6. Рівняння Пуассона та Лапласа Нагадаємо
- 24. Після інтегрування рівняння Пуассона отримаємо:
- 25. На рис. 2.9 наведено приклад представлення довільного
- 27. У зв’язку з тим, що заряд зосереджено
- 28. Перший доданок – нормальний складник у першому
- 29. .
- 30. Перший доданок характеризує перше середовищі, другий
- 32. Рис. 2.12 Складники вектора
- 33. З останнього рівняння та на
- 34. 2.7.4. Граничні умови на поверхні ідеального
- 36. Електрична енергія може накопичуватись не
- 37. 2.9. Висновки
- 39. 2.10. Контрольні питання та завдання 1. Поясніть
Слайд 2Зміст
2.1. Закон взаємодії електричних зарядів
2.2. Основні характеристики електричного поля
2.3. Закон Гауса
2.3.2. Закон Гауса в диференціальній формі
2.3.3. Перетворення (теорема) Гауса-Остроградського
2.4. Робота сил та потенціал електростатичного поля
2.5. Еквіпотенціальні поверхні. Градієнт потенціалу
2.6. Рівняння Пуассона та Лапласа
2.7. Граничні умови електростатики
2.7.1. Нормальні складники векторів та
2.7.2. Тангенціальні складники векторів та
2.7.3. Граничні умови для потенціалу
2.7.4. Граничні умови на поверхні ідеального провідника
2.8. Поняття електричної ємності. Енергія електростатичного поля
2.9. Висновки
2.10. Контрольні питання та завдання
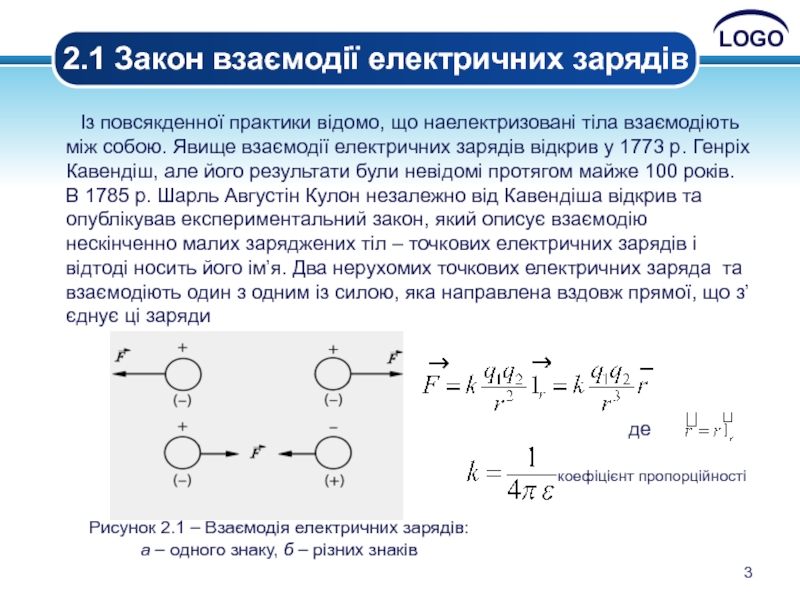
Слайд 3 Із повсякденної практики відомо, що наелектризовані тіла
де
Рисунок 2.1 – Взаємодія електричних зарядів:
а – одного знаку, б – різних знаків
коефіцієнт пропорційності
2.1 Закон взаємодії електричних зарядів
Слайд 42.2 Основні характеристики електричного поля
2.2. Основні характеристики електричного поля
На
Тобто напруженість електричного поля – це характеристика силової дії поля на пробний точковий заряд , якщо припустити, що внесення його у поле не впливає безпосередньо на розташування, зарядів які створюють це поле. E = [В/м] = [Н/Кл].
Слайд 5 Напруженість електричного поля залежить від середовища, що характеризує діелектрична
.
Слайд 6 Для однорідного лінійного ізотропного середовища (середовища, фізичні властивості яких у
де – відносна діелектрична сприйнятливість.
Діелектрична сприйнятливість – це величина, яка характеризує здатність діелектриків поляризуватися в електричному полі, що є скалярною для ізотропної речовини і яку визначають як відношення модуля поляризованості до модуля напруженості електричного поля, та тензорною для анізотропної речовини.
Слайд 7 Визначимо вектор електричного зміщення із урахуванням поляризованості:
де
– відносна діелектрична сприйнятливість,
– відносна діелектрична проникність.
– діелектрична проникність у вакуумі (електрична стала).
Таким чином, абсолютна діелектрична проникність – це величина, яка характеризує діелектричні властивості матеріалу діелектрика, яка є скалярною для ізотропної речовини і дорівнює відношенню модуля електричного зміщення до модуля напруженості електричного поля, та тензорною – для анізотропної речовини, тобто – це перше матеріальне рівняння:
Слайд 8 Параметр характеризує діелектричне середовище. За станом змінення параметрів,
Поле може бути гармонічним – величина, яка характеризує поле має одну гармоніку (монохромним), або може мати багато гармонік, його характеризують спектральною густиною.
Для монохромного поля та неоднорідного лінійного ізотропного середовища діелектрична проникність у загальному випадку є функція узагальнених криволінійних координат :
Слайд 9 Для монохромного поля та однорідного нелінійного ізотропного середовища діелектрична проникність
Для монохромного поля та однорідного лінійного анізотропного середовища маємо
У скороченій формі:
Запровадження вектора електричного зміщення доцільне також для дослідження поля в неоднорідних середовищах.
Слайд 10 Нехай маємо поле точкового заряду, розрахуємо умовну кількість силових
Стосовно сфери потік вектора
Слайд 11
2.3 Закон Гаусса
Рисунок 2.3 – Приклад орієнтації векторів
2.3.1. Закон Гаусса в інтегральній формі
Рисунок 2.4. До визначення поняття тілесний кут
Міра тілесного кута – співвідношення площі елемента сферичної поверхні до квадрату відстані з урахуванням орієнтації.
Слайд 12Нехай вектор , який створено зарядом , перетинає нескінченно малу площину
Орієнтація площини у просторі ( яку характеризує вектор-площадка) є принципово-важливим фактором під час аналізу векторних величин.
Слайд 13Закон Гаусса в інтегральній формі свідчить, що потік вектора електричного зміщення
- закон Гаусса в інтегральній формі
Слайд 142.3.2. Закон Гауса в диференціальній формі
Рисунок 2.5 – Визначення закону Гаусса
Слайд 15Визначимо будь-яку точку (x,y,z) у просторі, в якому є електричне поле.
Отже, маємо замкнену поверхню, за формою елементарного кубу з центром у точці із сторонами довжиною , та застосуємо закон Гаусса, тобто визначимо потік вектора крізь цей куб за формулою :
Для визначення цього інтегралу треба розкласти його на шість складників – відповідно кожній поверхні куба:
Слайд 16Оскільки елемент поверхні дуже малий, значення модуля вектора на ньому можна
де потрібно визначити на цій поверхні куба, , 1234.
Ця поверхня є на відстані х від точки, тому
де – значення в точці ; частинна похідна визначає змінення значення вздовж осі .
Слайд 17Додамо інтеграли (1234) та (5678), й отримаємо:
(2) (3)
Об’єднанням формул (1)…(2) (за всіма поверхнями) маємо:
Слайд 18Таким чином, застосовано закон Гауса для обмеженого простору – елементарного об’єму
Зауважимо, що операція змінює одиницю вимірювання відповідної функції на м-1 (до речі, теж саме притаманне операціям та ).
Із застосуванням оператора Гамільтона – «набла» –
Слайд 19Якщо врахувати, що потоку можна приписати алгебраїчний знак, то немає необхідності
Дивергенція - це лінійний диференційний оператор на векторному полі, що характеризує потік даного поля через поверхню досить малої (в умовах конкретного завдання) околиці кожної внутрішньої точки області визначення поля.
Слайд 20
.
2.3.3 Перетворення (теорема) Гауса-Остроградського
З’ясуємо взаємозв’язок сумарного заряду в об’ємі
(2.3-24)
та
(2.36)
Тоді з урахуванням (2.35) маємо:
(2.37)
Це співвідношення отримало назву перетворення (теорема) Гаусса-Остроградського – потік вектора через замкнену поверхню дорівнює інтегралу від дивергенції цього вектора, за об’ємом, обмеженим цією поверхнею. Тобто воно пов’язує об’ємний інтеграл з поверхневим і дозволяє змінювати порядок інтегрування.
Слайд 21Рисунок 2.7 – Замкнутий контур
.
З’ясуємо ситуацію таку, що в електростатичному полі точкового заряду в деякому просторі переміщується пробний заряд за траєкторією (рис. 2.6).
2.4. Робота сил та потенціал електростатичного поля
.
Рисунок 2.6 – Траєкторія руху заряду
Робота сил електростатичного поля не залежить від форми траєкторії, а визначена найкоротшою відстанню між початковою та кінцевими точками. Сили, робота яких не залежить від траєкторії, називають консервативними.
.
Це важливе співвідношення свідчить про те, що напруженість електричного поля можна визначити як градієнт скалярної величини – потенціала . Пояснимо, що знак “–” має фізичний зміст, бо напрями векторів та grad – протилежні (див. рис. 2.8). З формули (2.48) випливає, що за відомим значенням потенціалу можна розв’язати пряму задачу електростатики, якщо відомий зв’язок між потенціалом та густиною заряду. Цей зв’язок отримаємо із розв’язку рівняння Пуассона.
Слайд 22
.
.
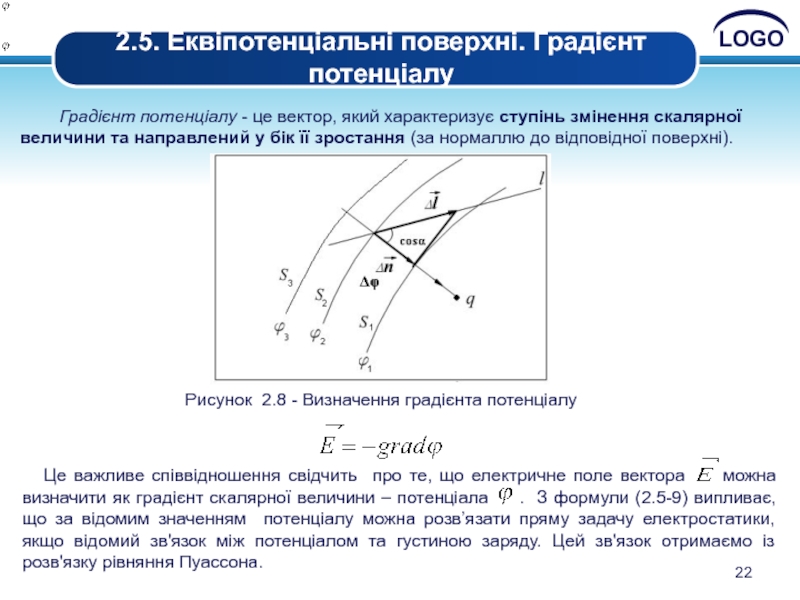
2.5. Еквіпотенціальні поверхні. Градієнт потенціалу
Градієнт
Рисунок 2.8 - Визначення градієнта потенціалу
Це важливе співвідношення свідчить про те, що електричне поле вектора можна визначити як градієнт скалярної величини – потенціала . З формули (2.5-9) випливає, що за відомим значенням потенціалу можна розв’язати пряму задачу електростатики, якщо відомий зв'язок між потенціалом та густиною заряду. Цей зв'язок отримаємо із розв'язку рівняння Пуассона.
Слайд 232.6. Рівняння Пуассона та Лапласа
Нагадаємо закон Гауса в диференціальній формі
З
- рівняння Пуассона
Математичний розв’язок цього рівняння:
Слайд 24Після інтегрування рівняння Пуассона отримаємо:
Якщо в деякому об’ємі заряди відсутні, то:
Розв’язок рівняння Лапласа визначають як добуток функцій однієї змінної
Слайд 25На рис. 2.9 наведено приклад представлення довільного вектора
Рисунок 2.9 – Вектор та його проекції , .
Аналогічно на межі поділу двох середовищ з різними значеннями діелектричної проникності ( 1 та 2) вектори, які описують електричне поле та можуть бути представлені двома складниками:
нормальним (проекцією на нормаль до границі вздовж осі y)
тангенціальним, або дотичним складником (проекція на границю розподілу вздовж осі у).
.
.
:
2.7. Граничні умови електростатики
Слайд 26
:
2.7.1. Нормальні складники векторів та
Щоб визначити нормальний складник зручним є вибір вектора як такого, що характеризує потік, який пронизує межу поділу.
Рисунок 2.10 – До визначення нормальних складників електричного поля
:
Відповідно до закону Гауса в інтегральній формі маємо визначення потоку вектора , який дорівнює сумарному заряду в об’ємі, обмеженому поверхнею S:
Розглянемо циліндр з поперечним перерізом , верхньою та нижньою основами . Відносно циліндра потік вектора – це сума потоків крізь верхню, нижню та бічну поверхні.
Слайд 27У зв’язку з тим, що заряд зосереджено на поверхні, висоту циліндра
Перший доданок характеризує стан поля у першому середовищі, а другий – у другому. Зменшуємо площу так, щоб можна було вважати, що в кожній точці цієї поверхні .
Тоді:
або
Слайд 28Перший доданок – нормальний складник у першому середовищі
Тоді граничні умови нормального складника вектора :
тобто нормальний складник вектора за наявності поверхневого заряду зазнає стрибок. Стосовно складників вектора , маємо:
В окремому випадку, якщо поверхневий заряд відсутній
Отже, нормальний складник вектора напруженості електричного поля змінюється стрибком.
Слайд 29
.
.
Для визначення тангенціального складника зручним є вибір вектора ,
2.7.2. Тангенціальні складники векторів та
Рисунок 2.11 – До визначення тангенціальних складників електричного поля
Якщо наближати контур до межі середовищ, то інтеграли
дорівнюють нулю. Тоді
Слайд 30 Перший доданок характеризує перше середовищі, другий – друге. Сторони ab
З урахуванням та напрямків обходу контуру, отримаємо:
З урахуванням, що ab=cd та після скорочення, маємо:
Стосовно складників вектора маємо:
Слайд 31
2.7.3. Граничні умови для потенціалу
Розглянемо граничні умови для потенціалу електростатичного
Оберемо координати таким чином, що вісь х спрямовано вздовж межі двох середовищ, а вісь у – співпадає з напрямком нормалі до межі. Тоді отримаємо:
Слайд 33 З останнього рівняння та на підставі граничних умов для
Слайд 34
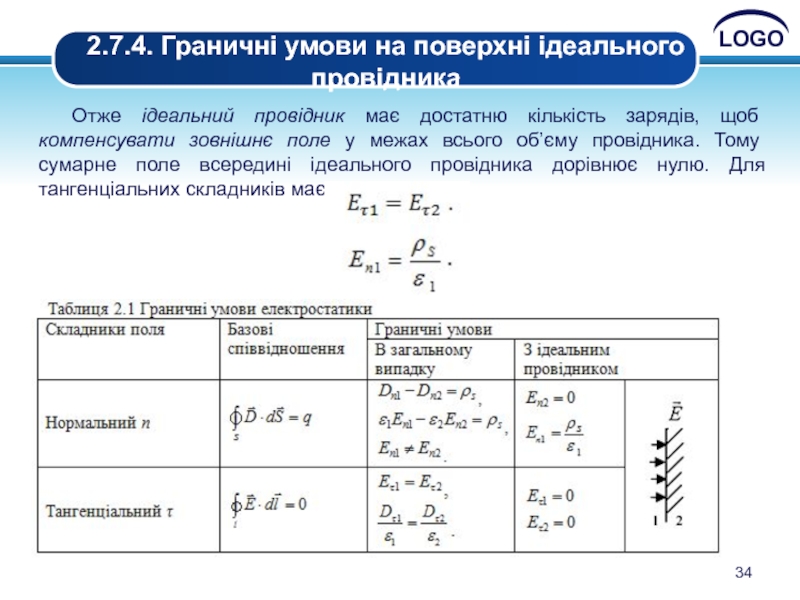
2.7.4. Граничні умови на поверхні ідеального провідника
Отже ідеальний провідник має
Слайд 35
2.8. Поняття електричної ємності. Енергія електростатичного поля
Нагадаємо, який компонент
За одиницю ємності прийнято ємність конденсатора, в якому накопичено заряд 1 Кл за умови, що до його обкладинок прикладино напругу 1 В. Ця одиниця має назву фарад [Ф]:1 Ф=1 Кл/1 В.
Перетворимо формулу, з урахуванням формул для ємності конденсатора з відстанню між пластинами d, та різниці потенціалів між його обкладинками
Слайд 36 Електрична енергія може накопичуватись не лише в конденсаторі, який
З урахуванням першого матеріального рівняння маємо рівність:
Відповідно електрична енергія зарядженого конденсатора дорівнює роботі, яку необхідно виконати, щоб його зарядити:
Слайд 392.10. Контрольні питання та завдання
1. Поясніть сутність закону Кулона, як прояву
2. Порівняйте силу взаємодії двох електронів: електричну, механічну.
3. Сформулюйте сутність та наведіть визначення напруженості як силової характеристики електричного поля; обґрунтуйте одиниці вимірювання.
4. Поясніть сутність та наведіть визначення вектора електричного зміщення.
5. Наведіть основні дескриптори електричного поля.
6. Поясніть сутність понять: поляризованість та діелектрична сприйнятливість.
7. Поясніть необхідність застосування поняття тензор.
8. Поясніть сутність фізичного та математичного поняття потік.
9. Сформулюйте сутність закону Гауса в інтегральній формі.
10. Виведіть формулу для закону Гауса в диференціальній формі.
11. Поясніть фізичну сутність поняття дивергенція.
12. Доведіть теорему (перетворення) Гауса-Остроградського.
13.Опишіть роботу сил під час руху електричного заряду в електричному полі.
14. Обґрунтуйте співвідношення інтегральне та диференціальне між напруженістю електричного поля та потенціалом.
15. Наведіть сутність понять градієнт, потенціал та еквіпотенціальна поверхня.
16. Сформулюйте рівняння Пуассона та наведіть його розв’язок.
17. Поясніть сутність граничних умов електростатики.
18. Обґрунтуйте співвідношення для нормальних складників векторів електричного поля.
19. Обґрунтуйте співвідношення для тангенціальних складників векторів електричного поля.
20. Поясніть граничні умові для векторів електричного поля, якщо одне середовище – ідеальний провідник.
21. Поясніть граничні умови для потенціалу.
22. Поясніть сутність поняття електрична ємність.
23. Виведіть формулу для ємності плаского конденсатора.
24. Виведіть формулу для питомої та повної енергії електричного поля.