- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 37. Дифракция Фраунгофера презентация
Содержание
- 1. Лекция 37. Дифракция Фраунгофера
- 2. (Дифракция Фраунгофера – это дифракция в пара-ллельных
- 3.
- 4. главный максимум. На него приходится более
- 5. Пятиминутка: На щель шириной b = 0,05
- 6. Дифракция на проволоке. Принцип Бабине. Для
- 7. Обозначим распределение поля на экране в слу-чае
- 8. Таким образом, сумма распределений полей от дополнительных
- 9. Дифракционная решетка. Дифракционная решётка - оптический прибор,
- 10. При освещении решётки монохроматическим светом на её
- 11. Оптическая схема анализатора спектра с дифрак-ционной решеткой:
- 12. Рассмотрим простейшую дифракционную решет-ку, работающую на пропускание.
- 13.
- 14. Оценим амплитуду дифрагировавшей волны и ее зависимость
- 15. Направление главного максимума соответствует условию, когда дуга
- 16. Сравним условия дифракционного максимума (37.5) и дифракционного
- 17. Определим угловую ширину какого-либо главного максимума как
- 18. Произведение Nd – это общая ширина решетки.
- 19. Обычно пользуются величиной относительного разрешения – Δλ/λ=1/(Nm).
- 20. Вернемся к дифракции Фраунгофера на щели. Если
- 21. Условно можно принять, что изображения двух светящихся
- 22.
- 23. Дифракция рентгеновских лучей в кристаллах Падающая на
- 24. Длина волны видимого света значительно превы-шает межатомные
- 25. Лучи отражаются от параллельного поверхности семейства атомных
- 26. Исследование дифракционного рассеяния рентгеновских лучей составляет целую
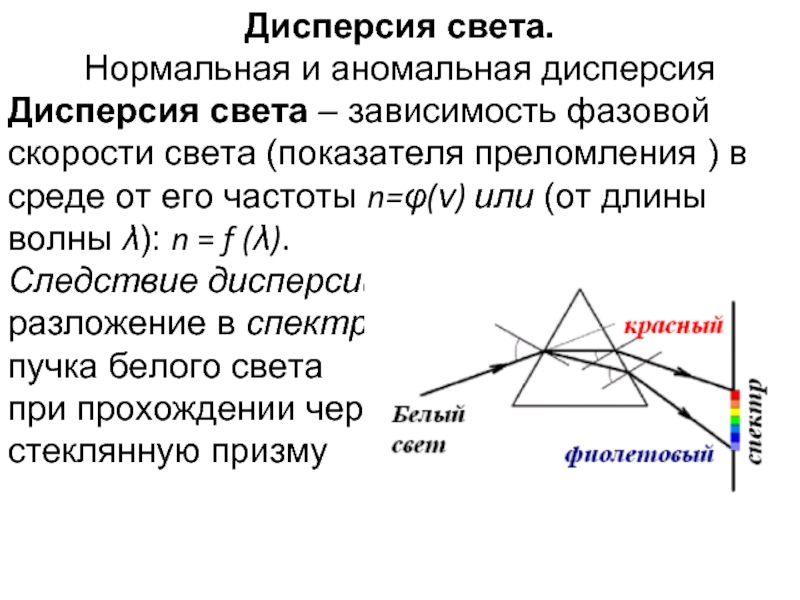
- 27. Дисперсия света. Нормальная и аномальная дисперсия
- 28.
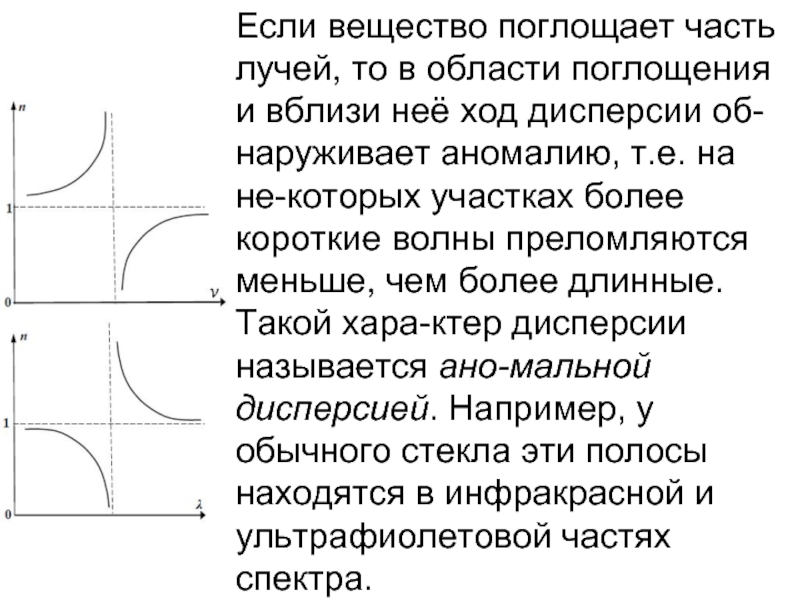
- 29. Нормальная дисперсия света наблюдается у веществ прозрачных
- 30. Если вещество поглощает часть лучей, то в
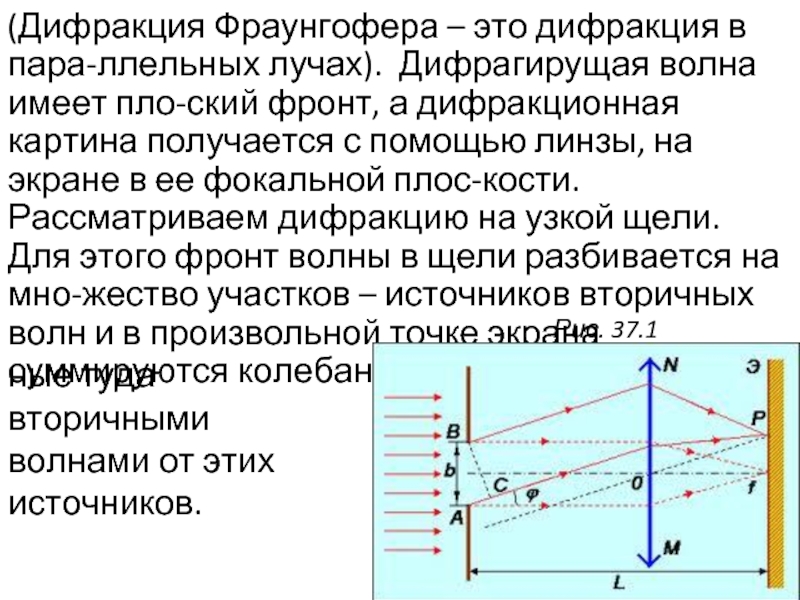
Слайд 2(Дифракция Фраунгофера – это дифракция в пара-ллельных лучах). Дифрагирущая волна имеет
ные туда вторичными волнами от этих источников.
Рис. 37.1
Слайд 4
главный максимум. На него приходится более 90% светового потока. Однако боковые
Рис. 37.2
Слайд 5Пятиминутка: На щель шириной b = 0,05 мм падает нормально монохроматический
Слайд 6Дифракция на проволоке. Принцип Бабине.
Для нахождения дифракционной картины от проволоки
Слайд 7Обозначим распределение поля на экране в слу-чае дифракции на щели Uщ(φ),
Слайд 8Таким образом, сумма распределений полей от дополнительных объектов равна полю, наблю-даемому
Если исходное поле U0 (φ) пучок параллельных лу-чей, идущих под углом φ =0, то для φ ≠0 U0 (φ)=0. В этом случае для φ ≠0 принцип Бабине дает
Uщ(φ)=-Uп(φ) = 0. Но интенсивность света – это квадрат амплитуды, следовательно при ϕ≠0 : Iщ(φ)=Iп(φ). (37.4)
Т.е. дифракционная картина от щели шириной d и проволоки той же толщины одинаковы, за исключением области φ =0.
Слайд 9Дифракционная решетка.
Дифракционная решётка - оптический прибор, предназначенный для анализа спектрального сос-тава
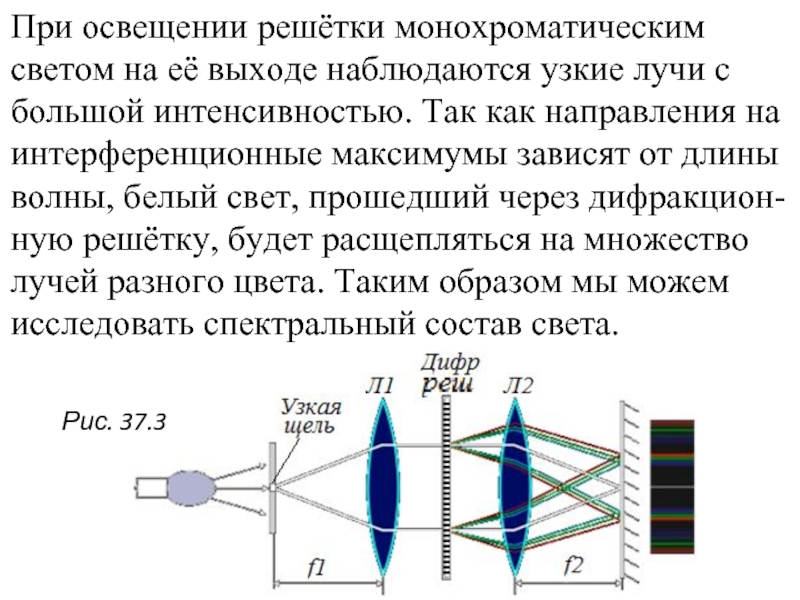
Слайд 10При освещении решётки монохроматическим светом на её выходе наблюдаются узкие лучи
Рис. 37.3
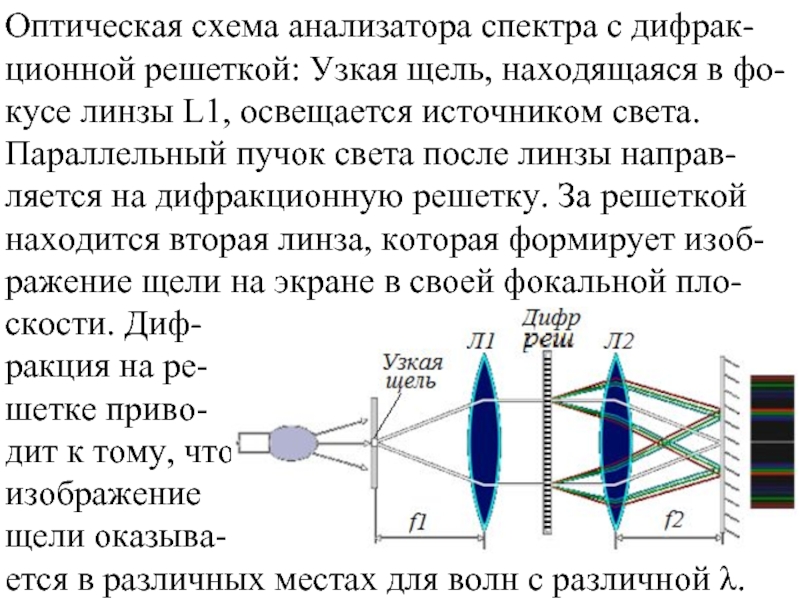
Слайд 11Оптическая схема анализатора спектра с дифрак-ционной решеткой: Узкая щель, находящаяся в
скости. Диф-
ракция на ре-
шетке приво-
дит к тому, что
изображение
щели оказыва-
ется в различных местах для волн с различной λ.
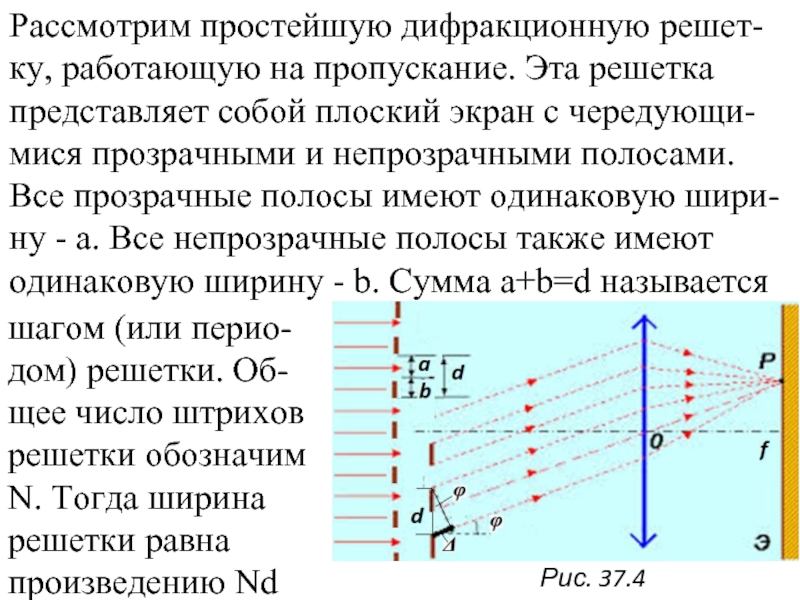
Слайд 12Рассмотрим простейшую дифракционную решет-ку, работающую на пропускание. Эта решетка представляет собой
шагом (или перио-дом) решетки. Об-щее число штрихов решетки обозначим N. Тогда ширина решетки равна произведению Nd
Рис. 37.4
Слайд 14Оценим амплитуду дифрагировавшей волны и ее зависимость от угла дифракции φ.
При изменении направления наблюдения φ дуга окружности будет сворачиваться или разворачи-ваться в дугу меньшего или большего радиуса при сохранении длины дуги.
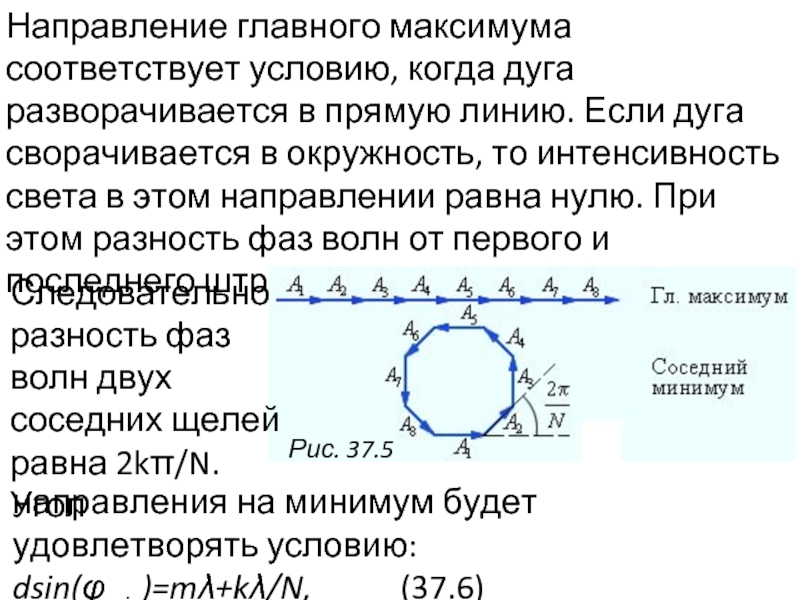
Слайд 15Направление главного максимума соответствует условию, когда дуга разворачивается в прямую линию.
Следовательно разность фаз волн двух соседних щелей равна 2kπ/N. Угол
направления на минимум будет удовлетворять условию: dsin(φmin)=mλ+kλ/N, (37.6)
где k – целое число от 1 до N-1
Рис. 37.5
Слайд 16Сравним условия дифракционного максимума (37.5) и дифракционного минимума (37.6)
dsin(φmax)=mλ, – условие
dsin(φmin)=mλ+kλ/N, – условие минимума (37.8)
Видим, что (37.6) является общей формулой экстремумов амплитуды светового вектора при дифракции на решетке. Если k=0 или k=N, формула выражает направление на максимум. В слачаях k=1, 2, 3…N-1, формула дает
угол направления на минимум.
Отсюда следует вывод о том, что
между соседними главными
максимумами находятся N-1
минимум.
Рис. 37.6
Слайд 17Определим угловую ширину какого-либо главного максимума как разность углов φmax- φmin
Взяв разность синусов углов максимума и ближайшего минимума, получим
dsin(φmax)- dsin(φmin)= λ/N. Используем тригонометрическую формулу
sin(α1)-sin(α2)=-2cos(α1/2+ α2/2)sin(α1/2-α2/2)
Поскольку углы φmax и φmin близки, можно записать
φmax- φmin=λ/(Ndcos(φmax)) (37.9)
Слайд 18Произведение Nd – это общая ширина решетки. С ее увеличением главные
Критерием разрешения двух спектральный линий с близкими длинами волн принято условие, при котором максимум одной волны приходится на минимум другой, который является ближайшим к ее максимуму. Это условие можно записать в виде формул:
dsin(φmax1)=mλ1=dsin(φmin2)=mλ2+ λ2/N
Из этого равенства получим
λ1- λ2=Δλ= λ2/(Nm) (37.10)
Слайд 19Обычно пользуются величиной относительного разрешения – Δλ/λ=1/(Nm). (37.11)
Разрешающая способность решетки определяется
Дифракционный предел разреше-ния оптических инструментов можно определить как минимальное расстоя-ние между двумя точечными источниками, ко-торые изображаются линзой в виде раздель-ных светлых пятен. Почему точечный источник изображается в виде пятна, а не точки?
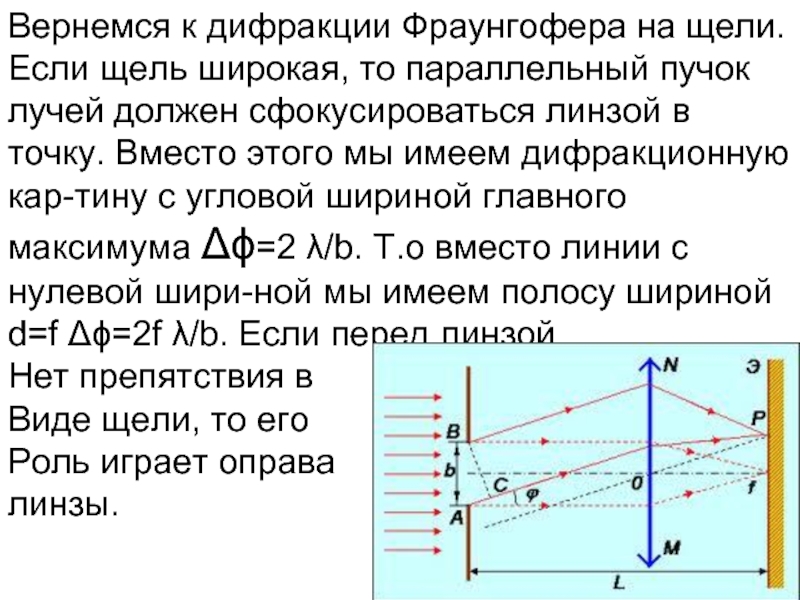
Слайд 20Вернемся к дифракции Фраунгофера на щели. Если щель широкая, то параллельный
Нет препятствия в
Виде щели, то его
Роль играет оправа
линзы.
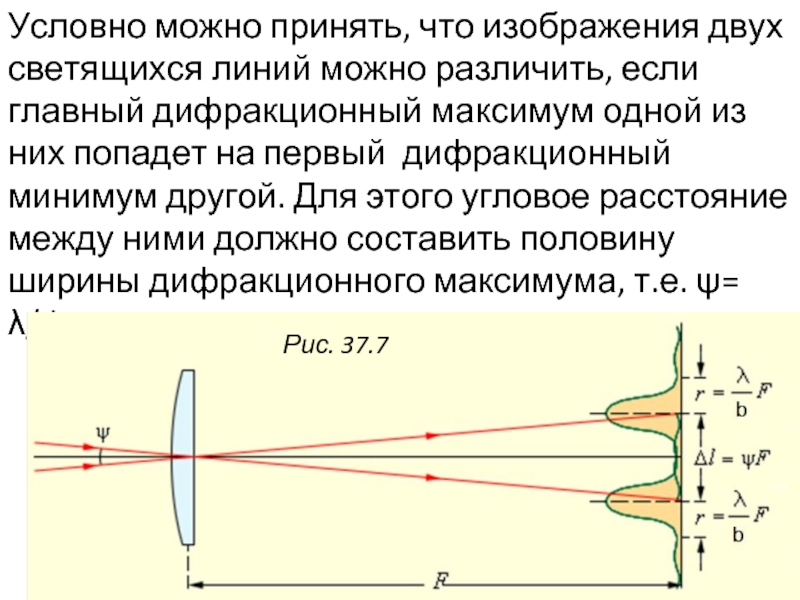
Слайд 21Условно можно принять, что изображения двух светящихся линий можно различить, если
Рис. 37.7
Слайд 23Дифракция рентгеновских лучей в кристаллах
Падающая на тело электромагнитная волна вызы-вает колебания
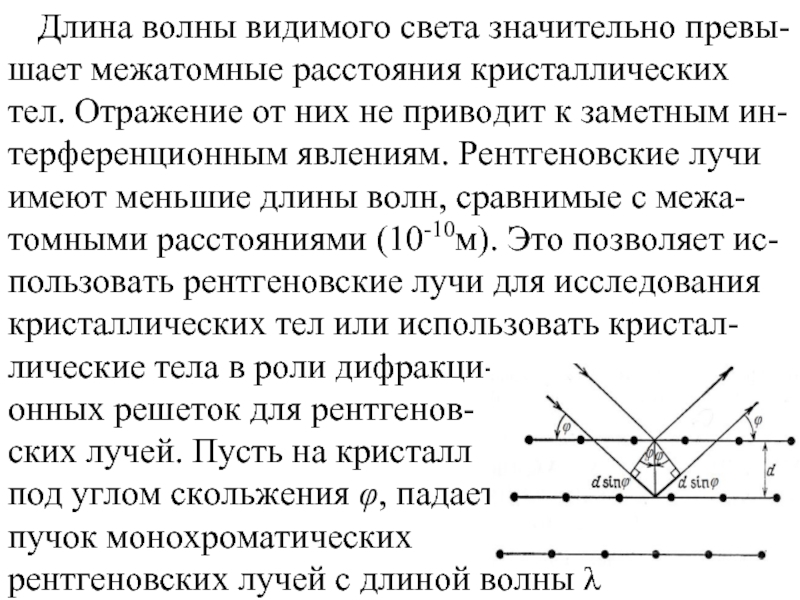
Слайд 24Длина волны видимого света значительно превы-шает межатомные расстояния кристаллических тел. Отражение
онных решеток для рентгенов-
ских лучей. Пусть на кристалл
под углом скольжения φ, падает параллельный пучок монохроматических
рентгеновских лучей с длиной волны λ
Слайд 25Лучи отражаются от параллельного поверхности семейства атомных плоскостей с межплоскостным расстоянием d под
2dsin(φ)=nλ (37.13)
Называют условием Вульфа-Брегов.
Слайд 26Исследование дифракционного рассеяния рентгеновских лучей составляет целую отрасль материаловедения – рентгеноструктурный
Пятиминутка: На грань кристалла падает параллельный пучок рентгеновских лучей с длиной волны 0.075 нм. Расстояние между атомными плоскостями равно 0.2 нм. Под каким углом скольжения следует направить лучи на поверхность, чтобы получить дифракционный максимум 1 порядка.
Слайд 27Дисперсия света.
Нормальная и аномальная дисперсия
Дисперсия света – зависимость фазовой
Следствие дисперсии:
разложение в спектр
пучка белого света
при прохождении через
стеклянную призму