- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 35. Дифракция света презентация
Содержание
- 1. Лекция 35. Дифракция света
- 2. Практическое использование интерференции света. Длина световых волн
- 3. Интерферометр Физо. Используется для определения плоскостности и
- 4. Интерферометр Майкельсона позволяет получить интерференцию лучей, отраженных
- 5. Интерферометр Жамена. Существуют двулучевые Ин-терферометры, предназначенные для
- 6. Просветление оптики, так называется уменьше-ние отражения света
- 7. Создание высокоотражающих диэлектрических зеркал. Металлические зеркала имеют
- 8. Пятиминутка. Вычислить толщину просветляющей пленки и требуемый
- 9. ДИФРАКЦИЯ СВЕТА
- 10. Дифракцией называется огибание волнами препятст-вий, встречающихся на
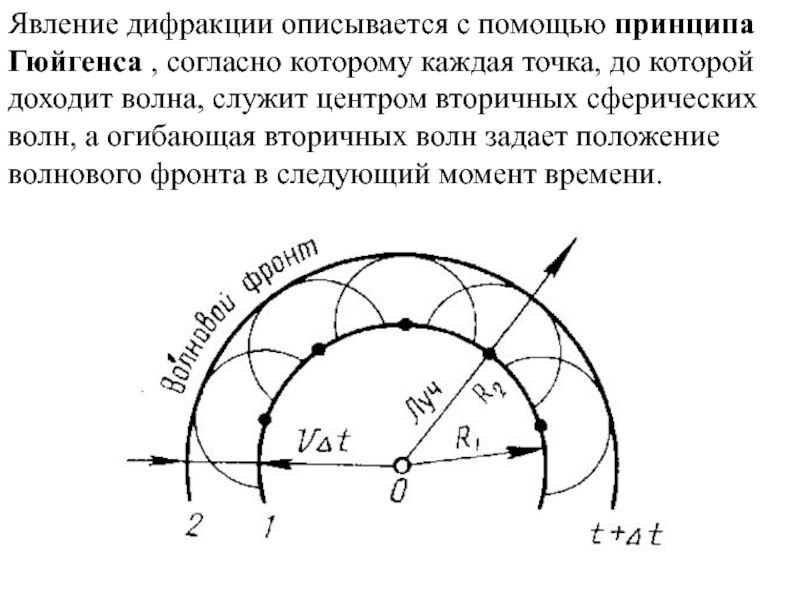
- 11. Явление дифракции описывается с помощью принципа Гюйгенса
- 12. Принцип Гюйгенса в его первоначальном виде позволяет
- 13. сивности света в точке Р необходимо просуммировать
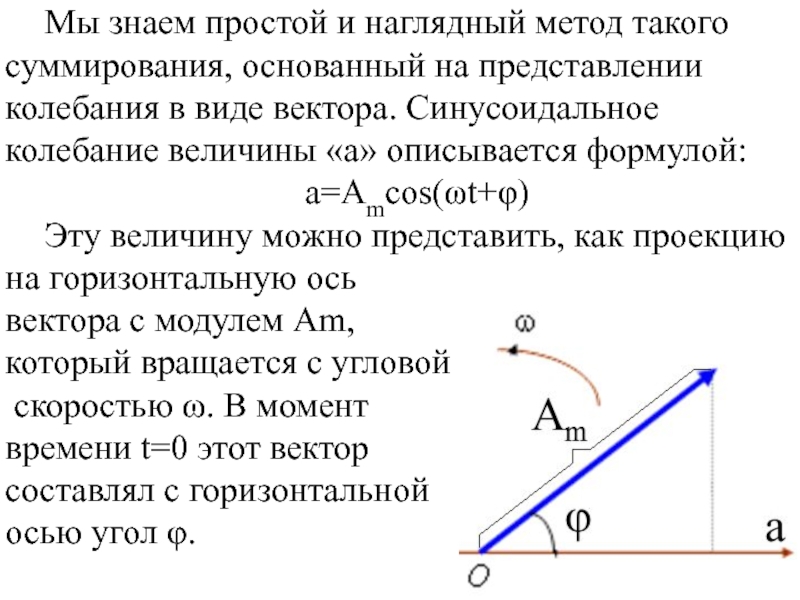
- 14. Мы знаем простой и наглядный метод такого
- 15. Предположим, что име- ется второе колебание b=Bmcos(ωt+θ)
- 16. Для определения этих величин просто сложим Векторы
- 17. Воспользуемся данным при- емом для нахождения интен-
- 18. При этом колебания, доставленные от точек одного
- 19. Длина этого вектора определит амплитуду светового вектора,
- 20. С увеличением номера кольцевого участка амплитуда колебаний
- 21. При этом спираль Френеля будет терять свои
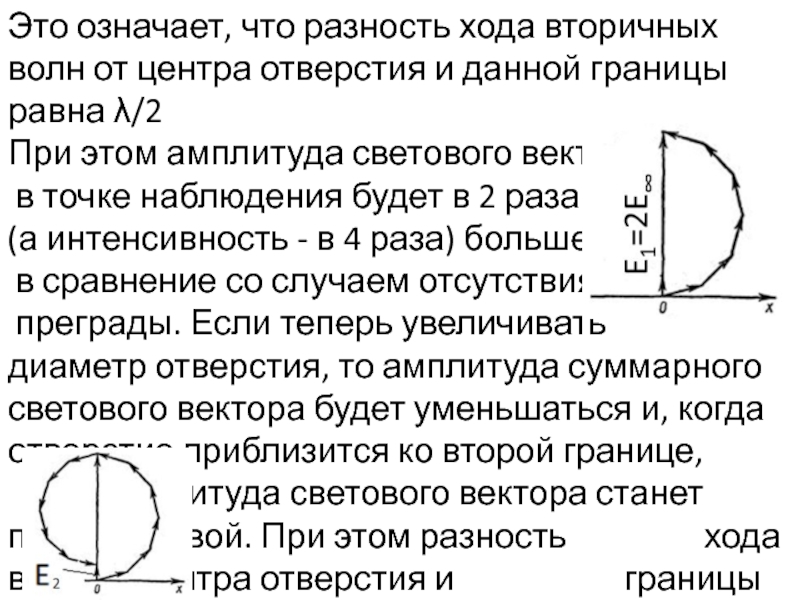
- 22. Это означает, что разность хода вторичных волн
- 23.
- 24.
- 25.
- 26.
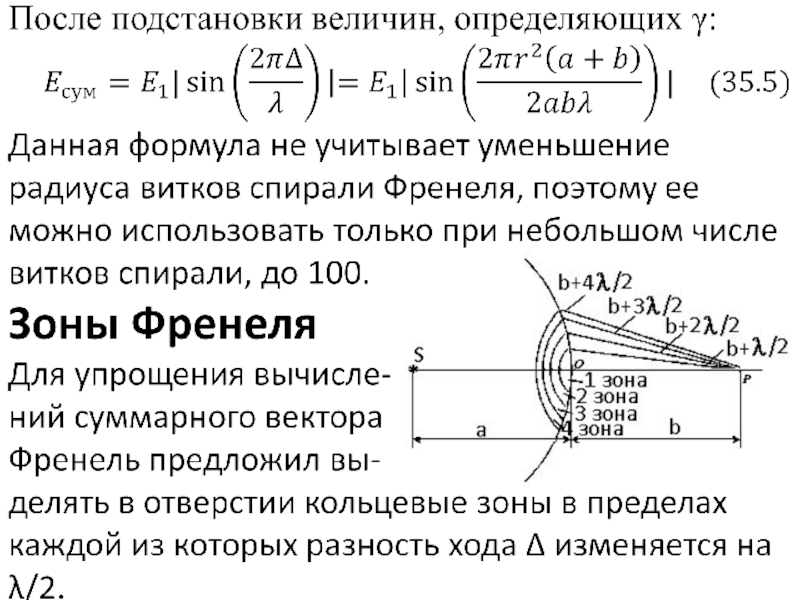
- 27. Пятиминутка. Сколько зон Френеля уместится в отверстии
- 28. Дифракционная картина от маленького отверстия представляет собой
- 29. В результате при вычислении освещенности центральной точки
- 30. В результате мы получаем плос-кую и тонкую линзу, очень по-лезную во мно-гих практичес-ких случаях.
- 31. Дифракция от круглого диска Диск закрывает
- 32. Светлое пятно в центре тени от диска
- 33. Разбиение на зоны ведется путем последовательного до
- 34. Один фокус дают волны проходящие на экран
- 35. Задача: Фазовая зонная пластинка изготавливается из стекла
Слайд 2Практическое использование интерференции света.
Длина световых волн составляет доли микрона. Непосредственно такие
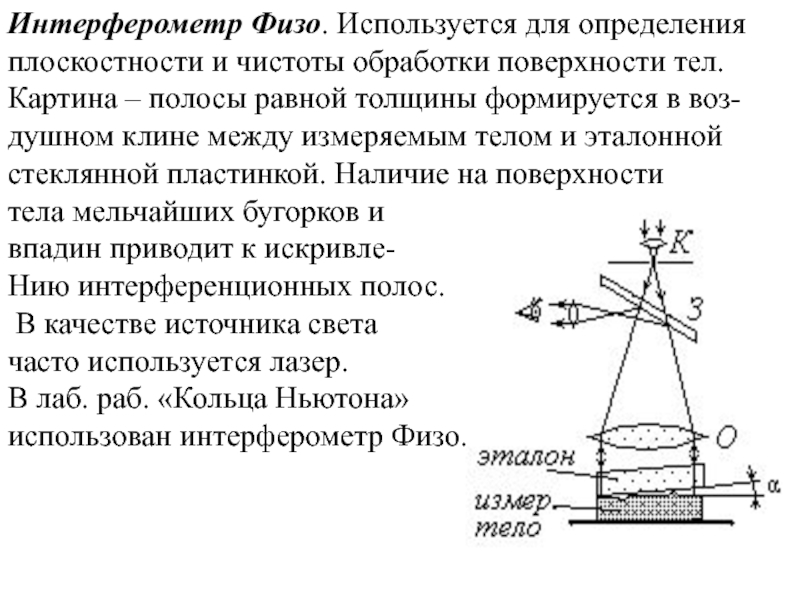
Слайд 3Интерферометр Физо. Используется для определения плоскостности и чистоты обработки поверхности тел.
тела мельчайших бугорков и
впадин приводит к искривле-
Нию интерференционных полос.
В качестве источника света
часто используется лазер.
В лаб. раб. «Кольца Ньютона»
использован интерферометр Физо.
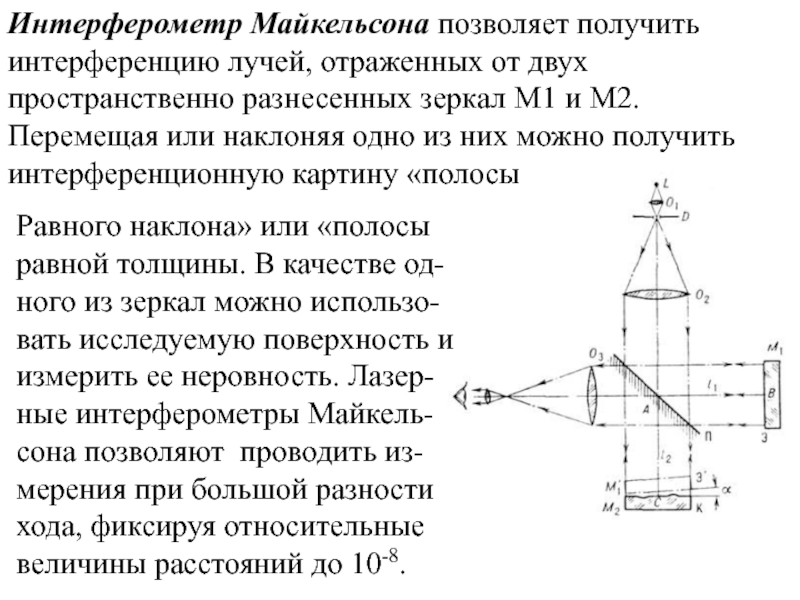
Слайд 4Интерферометр Майкельсона позволяет получить интерференцию лучей, отраженных от двух пространственно разнесенных
Равного наклона» или «полосы равной толщины. В качестве од-ного из зеркал можно использо-вать исследуемую поверхность и измерить ее неровность. Лазер-ные интерферометры Майкель-сона позволяют проводить из-мерения при большой разности хода, фиксируя относительные величины расстояний до 10-8.
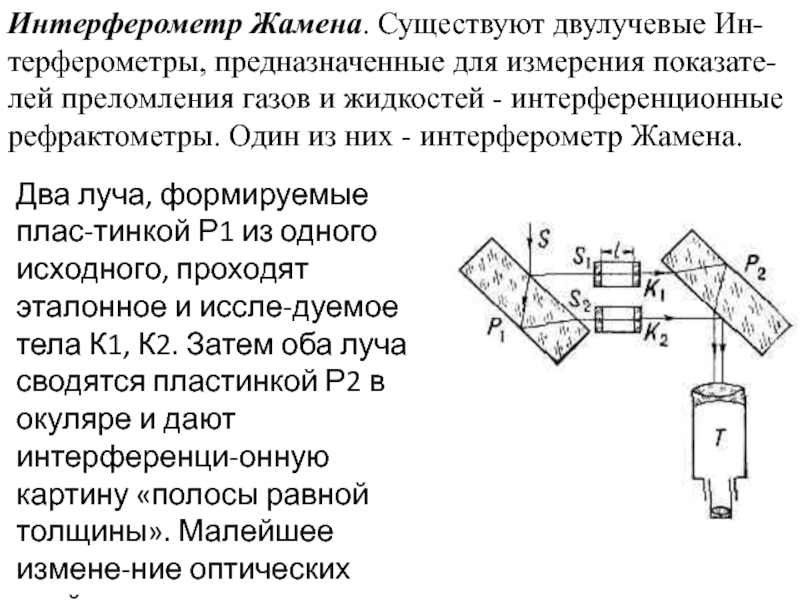
Слайд 5Интерферометр Жамена. Существуют двулучевые Ин-терферометры, предназначенные для измерения показате-лей преломления газов
Два луча, формируемые плас-тинкой Р1 из одного исходного, проходят эталонное и иссле-дуемое тела К1, К2. Затем оба луча сводятся пластинкой Р2 в окуляре и дают интерференци-онную картину «полосы равной толщины». Малейшее измене-ние оптических свойств иссле-дуемого тела приводит к сдвигу полос картины
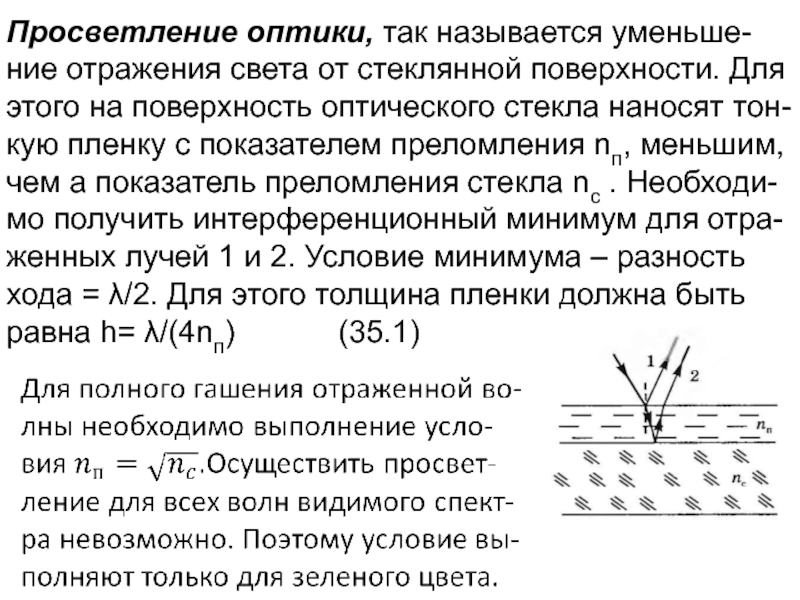
Слайд 6Просветление оптики, так называется уменьше-ние отражения света от стеклянной поверхности. Для
Слайд 7Создание высокоотражающих диэлектрических зеркал. Металлические зеркала имеют не очень хороший коэффи-циент
интерференционный максимум для отраженных от поверхностей раздела лучей. Поэтому внешняя пленка имеет максимальный коэффициент прелом-ления. Удается получить зеркала с коэффициентом отражения 0.99.
Слайд 8Пятиминутка. Вычислить толщину просветляющей пленки и требуемый показатель преломления ее материала,
Слайд 10Дифракцией называется огибание волнами препятст-вий, встречающихся на их пути, или в
ДИФРАКЦИЯ СВЕТА.
Слайд 11Явление дифракции описывается с помощью принципа Гюйгенса , согласно которому каждая
Слайд 12Принцип Гюйгенса в его первоначальном виде позволяет находить только положения волнового
Принцип Гюйгенса-Френеля
Гипотезу Гюйгенса об огибающей вторичных волн Френель дополнил физически ясным положением, согласно которому вторичные волны, приходя в точку наблюдения, интерферируют друг с другом. Рисунок иллюстрирует принцип Гюйгенса–Френеля.
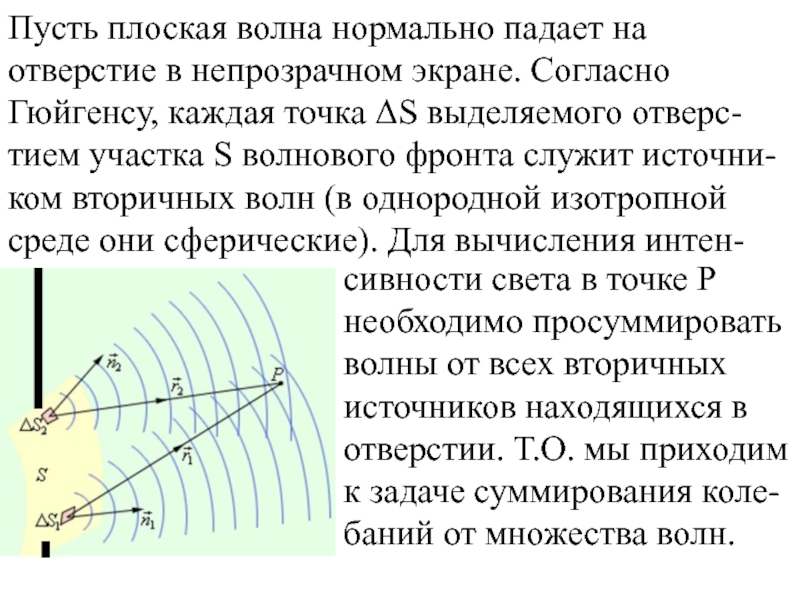
Слайд 13сивности света в точке Р необходимо просуммировать волны от всех вторичных
Пусть плоская волна нормально падает на отверстие в непрозрачном экране. Согласно Гюйгенсу, каждая точка ΔS выделяемого отверс-тием участка S волнового фронта служит источни-ком вторичных волн (в однородной изотропной среде они сферические). Для вычисления интен-
Слайд 14Мы знаем простой и наглядный метод такого суммирования, основанный на представлении
a=Amcos(ωt+φ)
Эту величину можно представить, как проекцию на горизонтальную ось
вектора с модулем Аm,
который вращается с угловой
скоростью ω. В момент
времени t=0 этот вектор
составлял с горизонтальной
осью угол φ.
Слайд 15Предположим, что име-
ется второе колебание
b=Bmcos(ωt+θ)
Мы также изобразим
его на той же
в виде вращающегося
вектора с длиной Вm
под углом θ к горизонтальной оси.
Пусть величины «а» и «b» складываются образуя колебание «с»:
с= Amcos(ωt+φ)+ Bmcos(ωt+θ)
Суммарное колебание также буде синусоидальным и иметь амплитуду Сm и начальную фазу ψ:φ
c=Cmcos(ωt+ψ)
Слайд 16Для определения этих величин просто сложим Векторы колебаний a и b,
Если суммируются несколько колебаний одинаковой частоты, то для нахождения вектора, изображающего суммарное колебание,
достаточно просуммировать векторы,
изображающие складываемые колеба-
ния. При этом сложение можно выпол-
нять путем подрисовывания к концу
текущего слагаемого начала следую-
щего, как это сделано на рисунке
Слайд 17Воспользуемся данным при-
емом для нахождения интен-
сивности света при дифрак-
ции на круглом
возьмем точку наблюде-
ния на перпендикуляре к
центру отверстия. Разобьем мысленно площадь отверстия на очень узкие кольцевые участки с оди-наковой площадью. В пределах каждого из них расстояние от любой его точки до точки наблю-дения одинаково. Каждая точка отверстия предс-тавляет собой источник вторичной волны, которая доставит в точку наблюдения колебание светового вектора.
Слайд 18При этом колебания, доставленные от точек одного кольцевого участка, будут иметь
Колебания, пришедшие от другой зоны будут иметь другую начальную
фазу и дадут изображаю-
щий вектор под другим уг-
лом. Просуммировав изоб-
ражающие векторы коле-
баний светового вектора
от всех зон, мы получим
вектор суммарного колебания.
Слайд 19Длина этого вектора определит амплитуду светового вектора, а квадрат амплитуды –
ти фаз колебаний от сосед-
них зон также получаться
одинаковыми. В результате
картина сложения изобража-
ющих векторов будет иметь
вид, показанный на рисунке.
Слайд 20С увеличением номера кольцевого участка амплитуда колебаний будет немного уменьшаться вследствие
уменьшать диаметр отверстия, то
внешние зоны, будут закрываться
и престанут давать вклад в суммар-
ный изображающий вектор.
Слайд 21При этом спираль Френеля будет терять свои центральные витки. Поскольку радиусы
Слайд 22Это означает, что разность хода вторичных волн от центра отверстия и
При этом амплитуда светового вектора
в точке наблюдения будет в 2 раза
(а интенсивность - в 4 раза) больше,
в сравнение со случаем отсутствия
преграды. Если теперь увеличивать
диаметр отверстия, то амплитуда суммарного светового вектора будет уменьшаться и, когда отверстие приблизится ко второй границе, амплитуда светового вектора станет почти нулевой. При этом разность хода волн от центра отверстия и границы зоны будет равна λ.
Слайд 27Пятиминутка. Сколько зон Френеля уместится в отверстии диаметром 0.5 мм, если
Слайд 28Дифракционная картина от маленького отверстия представляет собой чередование светлых и темных
Представим себе прозрачную пластинку на которую нанесены непрозрачные
кольца, закрывающие четные зоны
Френеля. Вклад этих зон в осве-
щенность центральной точки диф-
ракционной картины будет нуле-
вым.
Слайд 29В результате при вычислении освещенности центральной точки дифракционной картины вместо спирали
называют амплитудной, будет действовать подоб-но линзе, фокусируя лучи в центральной точке.
Еще более эффективной оказывается фазовая зонная пластинка, которая не отсекает свет четных зон Френеля, а увеличивает для них длину оптического пути на λ/2. Для этого на четных зонах пластинка чуть более толстая.
Слайд 30В результате мы получаем плос-кую и тонкую линзу, очень по-лезную во
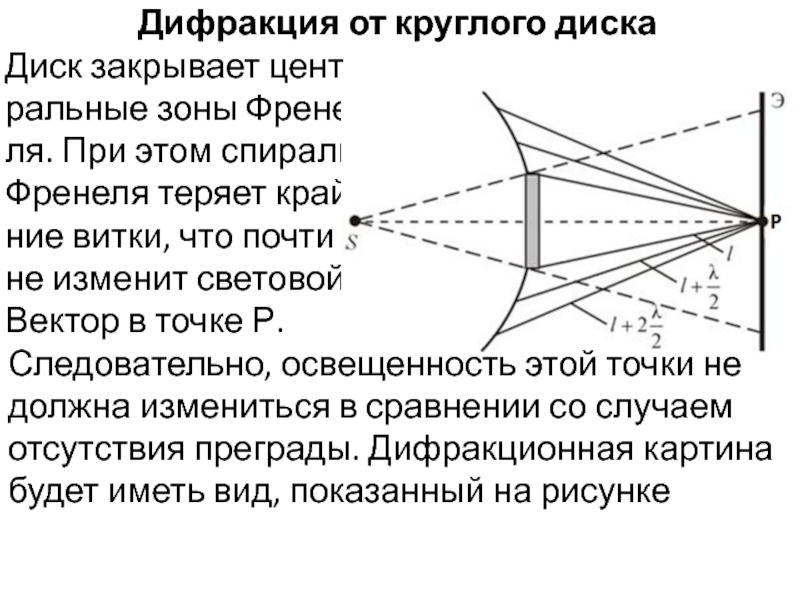
Слайд 31Дифракция от круглого диска
Диск закрывает цент-
ральные зоны Френе-
ля. При этом
Френеля теряет край-
ние витки, что почти
не изменит световой
Вектор в точке Р.
Следовательно, освещенность этой точки не должна измениться в сравнении со случаем отсутствия преграды. Дифракционная картина будет иметь вид, показанный на рисунке
Слайд 32Светлое пятно в центре тени от
диска называется пятном Пуассона.
При опытах
используют маленький шарик
Дифракция от прямого края полуплоскости
характеризуется проникновением части световой энергии в область геометрической тени. В осве-щенной области (справа от края полуплоскости) образуется система параллельных краю полос, период и контрастность которых убывают по мере удаления от границы
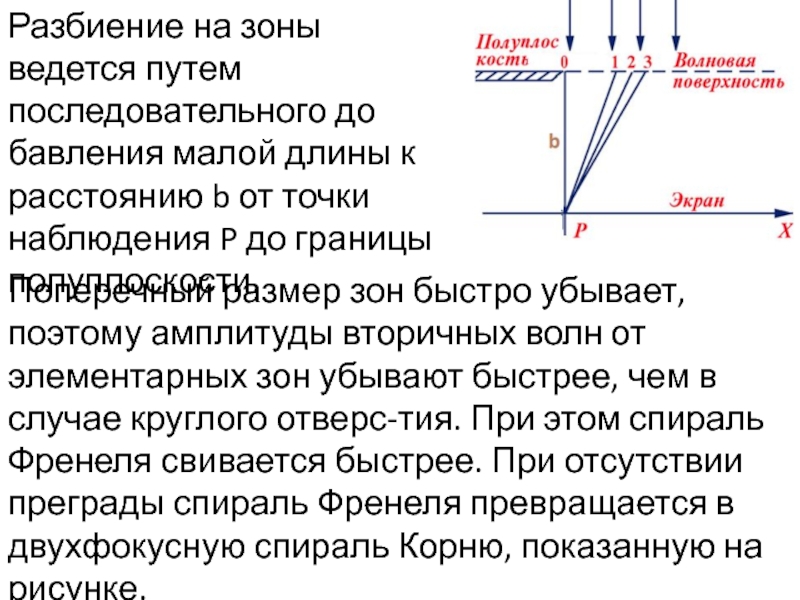
Слайд 33Разбиение на зоны ведется путем последовательного до
бавления малой длины к расстоянию
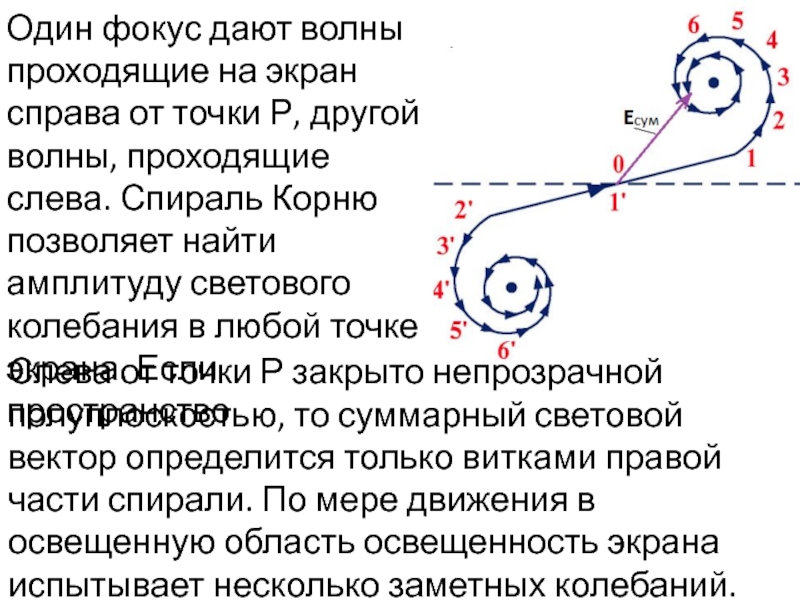
Поперечный размер зон быстро убывает, поэтому амплитуды вторичных волн от элементарных зон убывают быстрее, чем в случае круглого отверс-тия. При этом спираль Френеля свивается быстрее. При отсутствии преграды спираль Френеля превращается в двухфокусную спираль Корню, показанную на рисунке.
Слайд 34Один фокус дают волны проходящие на экран справа от точки Р,
Слева от точки Р закрыто непрозрачной полуплоскостью, то суммарный световой вектор определится только витками правой части спирали. По мере движения в освещенную область освещенность экрана испытывает несколько заметных колебаний.