- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 3: Волновая оптика. Дифракция. Фурье оптика презентация
Содержание
- 1. Лекция 3: Волновая оптика. Дифракция. Фурье оптика
- 2. Волновая оптика Свет описывается как скалярная волновая
- 3. Дифракция света Дифракция волн (лат. diffractus —
- 4. Теория дифракции Принцип Гюйгенса Френеля Огюстен Жан
- 5. Дифракция Френеля Число зон Френеля
- 6. Дифракция на круглом отверстии Метод разбиения волнового
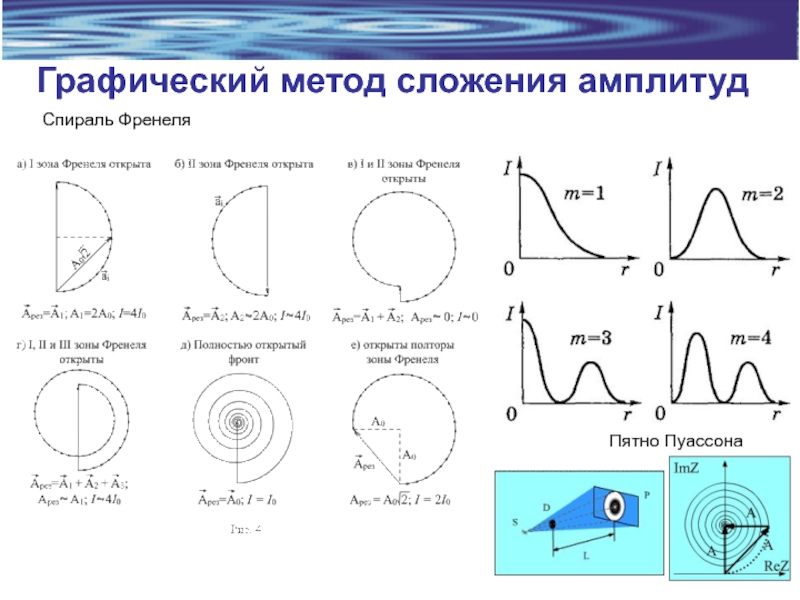
- 7. Графический метод сложения амплитуд Спираль Френеля Пятно Пуассона
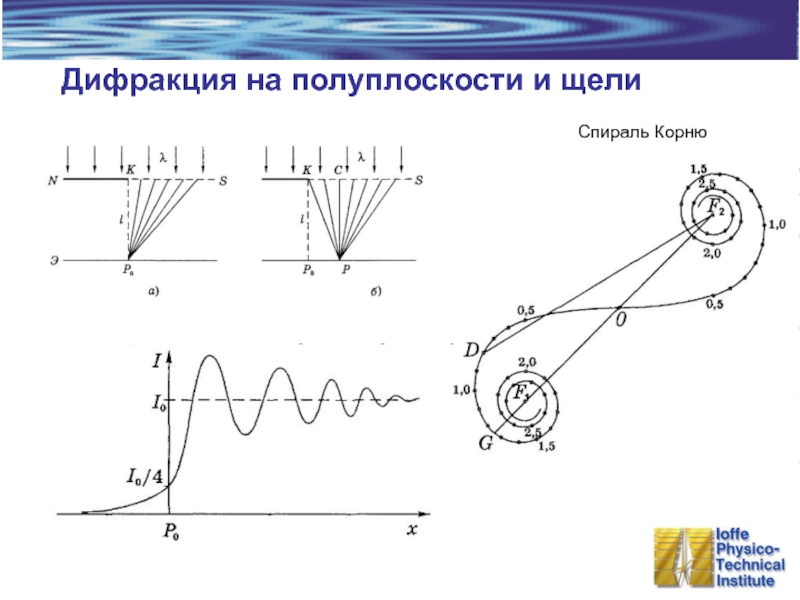
- 8. Дифракция на полуплоскости и щели Спираль Корню
- 9. Дифракция Фраунгофера Свет, распространяющийся в направлениях, отличных
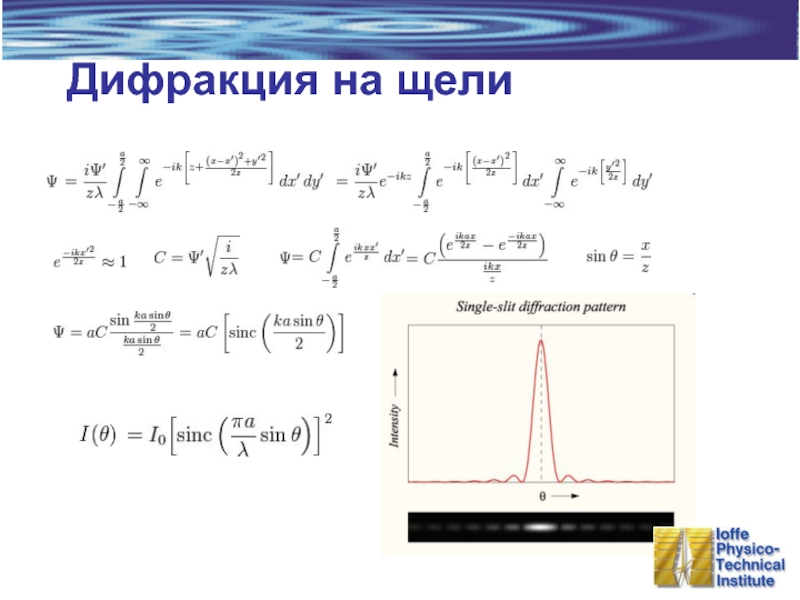
- 10. Дифракция на щели
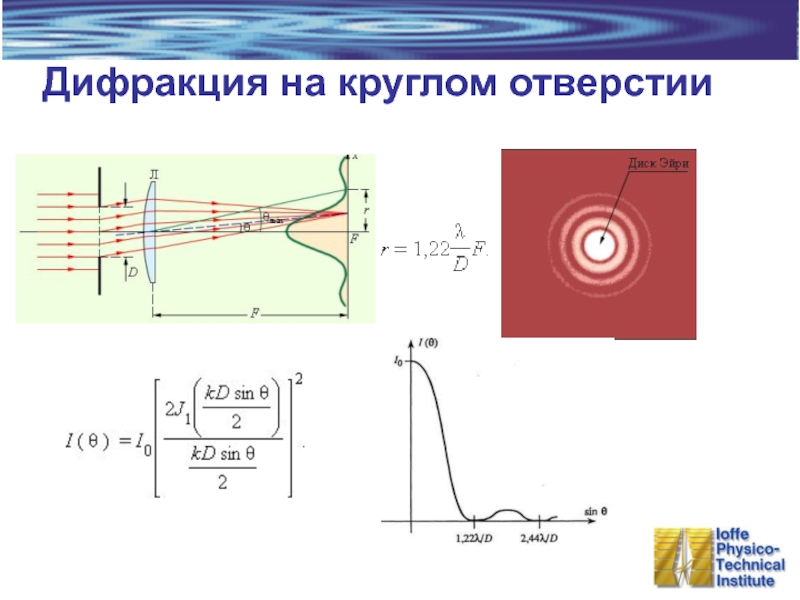
- 11. Дифракция на круглом отверстии
- 12. Дифракционная расходимость Лазерный пучок D0 = 2
- 13. Дифракционные оптические элементы Основные идеи: использование явления
- 14. Бессель-оптика и сингулярная оптика Винтовой фазовый ДОЭ
- 15. Разрешающая способность Критерий Рэлея Разрешающая способность глаза
- 16. Дифракционный предел Mинимально возможный размер светового
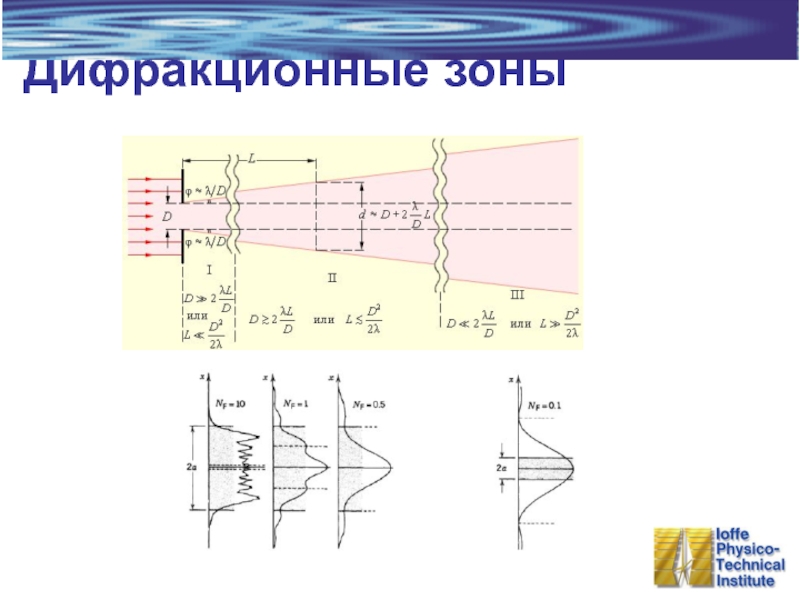
- 17. Дифракционные зоны
- 18. Ближнепольная оптика Дифракция на отверстии меньше длины волны (волновая оптика не работает)
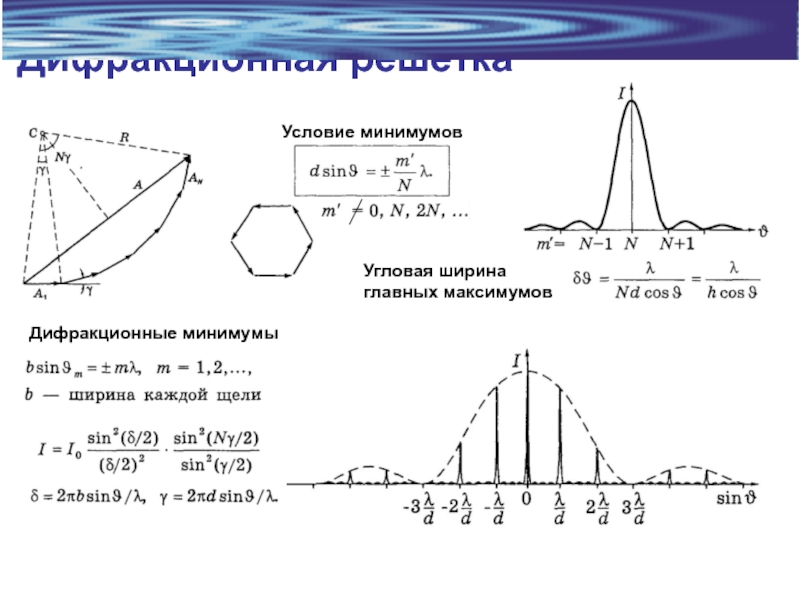
- 19. Дифракционная решетка Главные максимумы
- 20. Дифракционная решетка Условие минимумов Угловая ширина главных максимумов Дифракционные минимумы
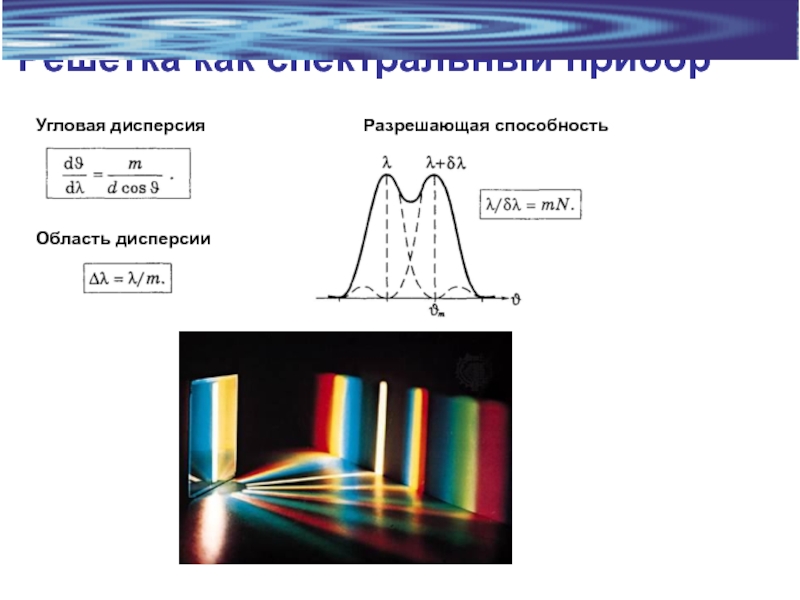
- 21. Решетка как спектральный прибор Угловая дисперсия Разрешающая способность Область дисперсии
- 22. Фурье оптика Гармонический анализ (Преобразование Фурье) Представление
- 23. Фурье оптика Плоские волны играют роль гармонических
- 24. Свободное пространство Параксиальном приближении По распределению амплитуды
- 25. Дифракционная решетка
- 26. Сферическая линза
- 27. Зонная пластика Френеля Зонная пластинка работает как
- 28. Передаточная функция Линейная функция инвариантная к сдвигу
- 29. Фурье преобразование Одна плоская волна соответствует каждой
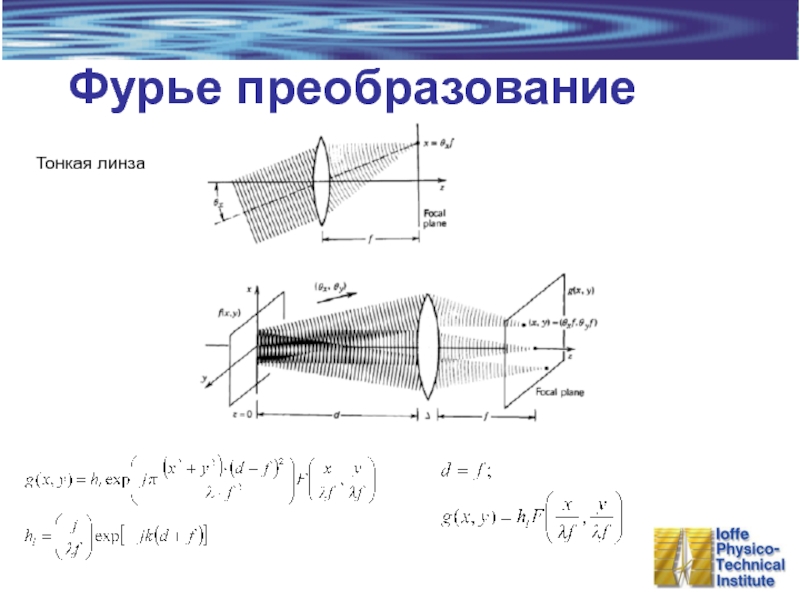
- 30. Тонкая линза Фурье преобразование
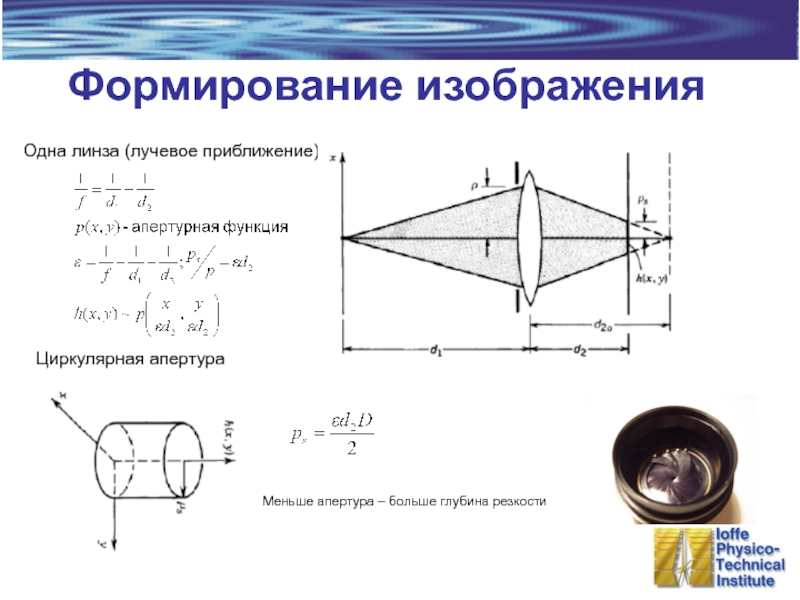
- 31. Одна линза (лучевое приближение) Формирование изображения Циркулярная апертура Меньше апертура – больше глубина резкости
- 32. 4f система Оптическая обработка изображений Перевернутое изображение с единичным увеличением
- 33. 4f система Пространственная фильтрация
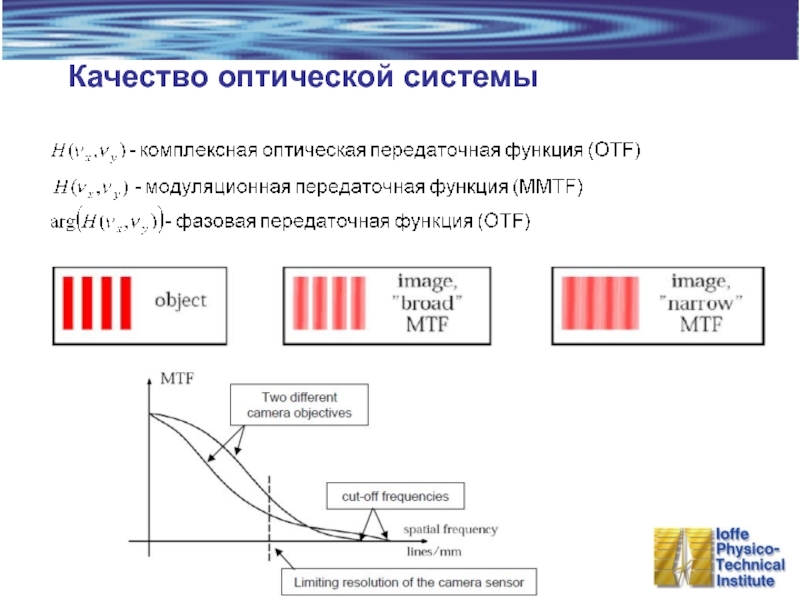
- 34. Качество оптической системы
Слайд 2Волновая оптика
Свет описывается как скалярная волновая функция (решение волнового уравнения)
Длина волны
Слайд 3Дифракция света
Дифракция волн (лат. diffractus — буквально разломанный, переломанный) — явление,
Первоначально понятие дифракции относилось к огибанию волнами препятствий, но в современном, более широком толковании, с дифракцией связывают весьма широкий круг явлений, возникающих при распространении волн в неоднородных средах, а также при распространении ограниченных в пространстве волн.
Дифракция тесно связана с явлением интерференции. Более того, само явление дифракции зачастую трактуют как частный случай интерференции (интерференция вторичных волн).
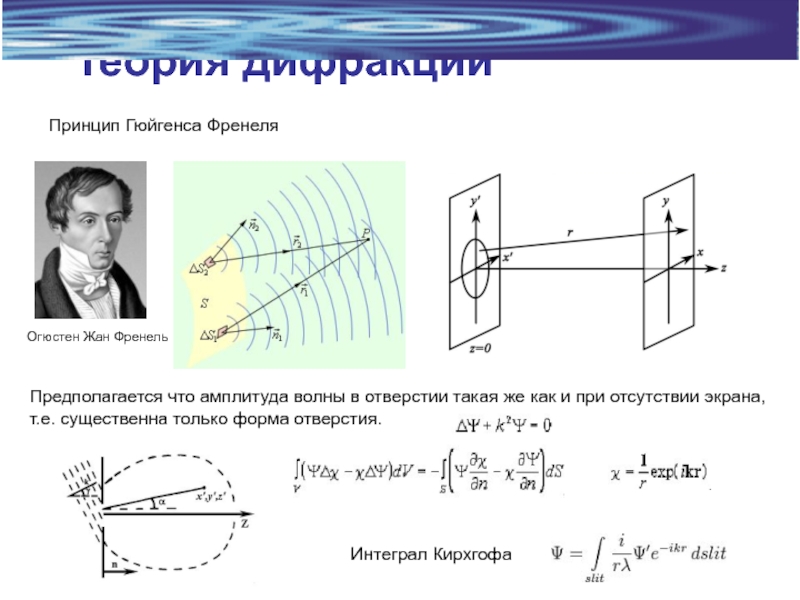
Слайд 4Теория дифракции
Принцип Гюйгенса Френеля
Огюстен Жан Френель
Предполагается что амплитуда волны в отверстии
т.е. существенна только форма отверстия.
Интеграл Кирхгофа
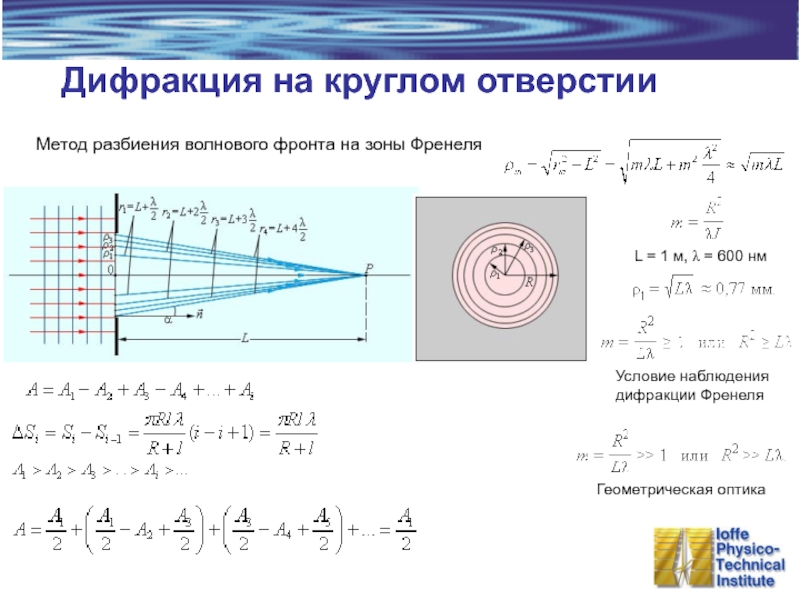
Слайд 6Дифракция на круглом отверстии
Метод разбиения волнового фронта на зоны Френеля
L
Условие наблюдения
дифракции Френеля
Геометрическая оптика
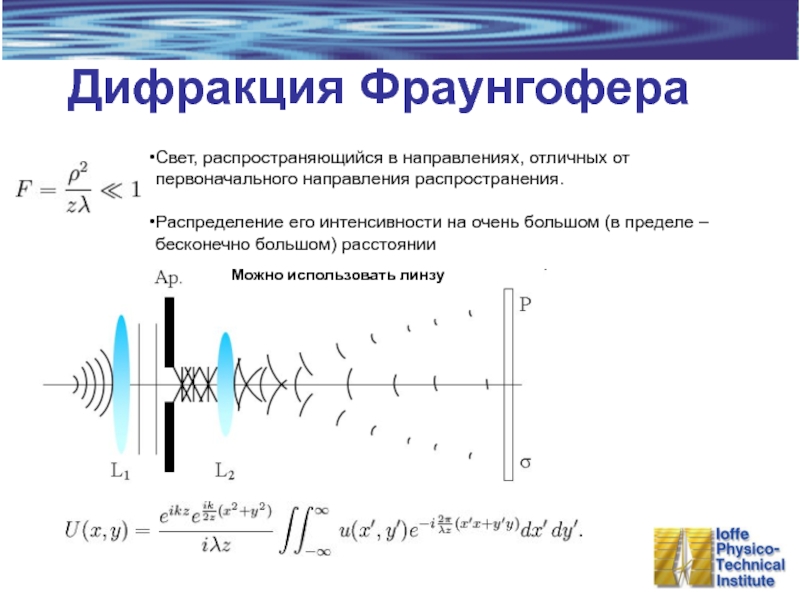
Слайд 9Дифракция Фраунгофера
Свет, распространяющийся в направлениях, отличных от первоначального направления распространения.
Распределение
Можно использовать линзу
Слайд 12Дифракционная расходимость
Лазерный пучок D0 = 2 мм, L = 100 м
D
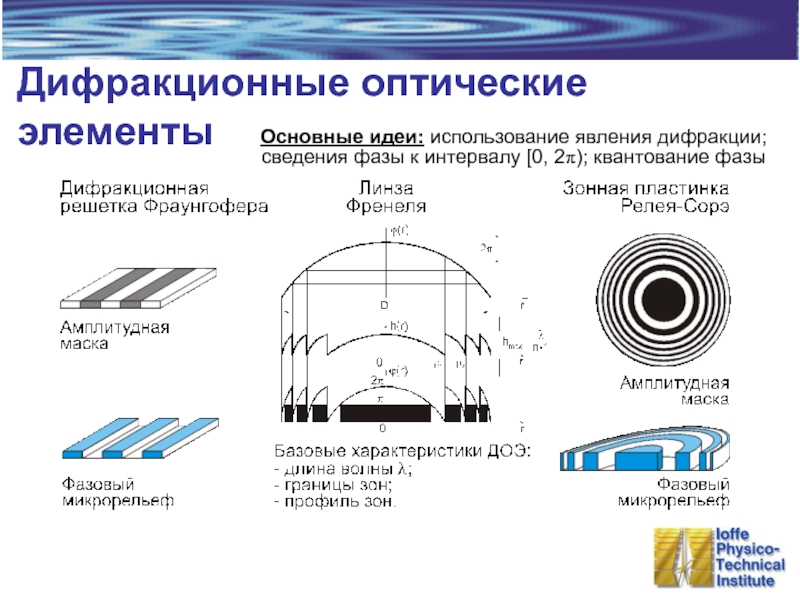
Слайд 13Дифракционные оптические элементы
Основные идеи: использование явления дифракции;
сведения фазы к интервалу
Слайд 14Бессель-оптика и сингулярная оптика
Винтовой фазовый ДОЭ
Винтовая
зонная пластина
Березный А.Е., Прохоров
Khonina S.N., Kotlyar V.V., Shinkaryev M.V., Soifer V.A., Uspleniev G.V., The phase rotor filter // J. Modern Optics, 1992
Решетка
с «вилкой»
Heckenberg N.R. et al. Generation of optical phase singularities by computer-generated holograms
// Opt. Lett., 1992
Bazhenov V.Yu., Soskin M.S., Vasnetsov M.V. Screw dislocations
in light wavefronts
// J. of Mod. Opt., 1992
m=1
Функция фазы терпит m разрывов первого рода, m – порядок ДОЭ
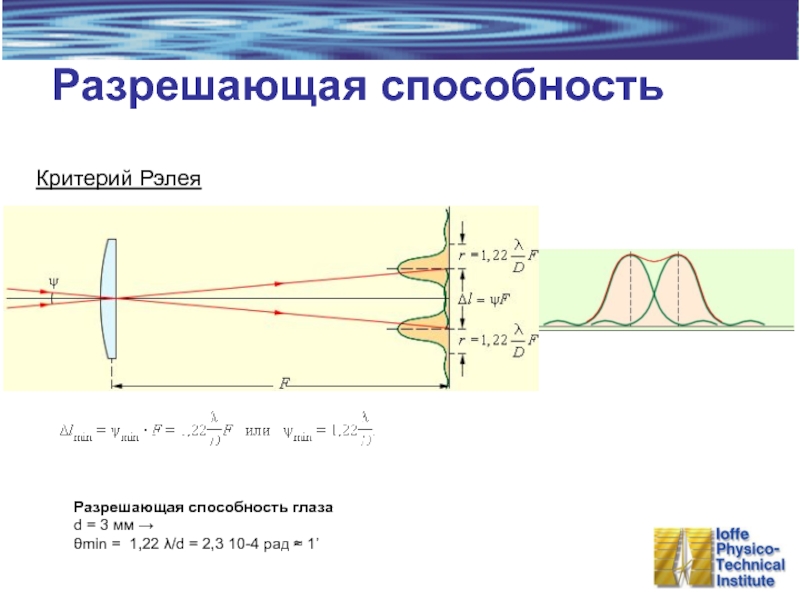
Слайд 15Разрешающая способность
Критерий Рэлея
Разрешающая способность глаза
d = 3 мм →
θmin =
Слайд 16Дифракционный предел
Mинимально возможный размер светового пятна,
которое можно получить, фокусируя свет
в среде с показателем преломления n:
Для микроскопа
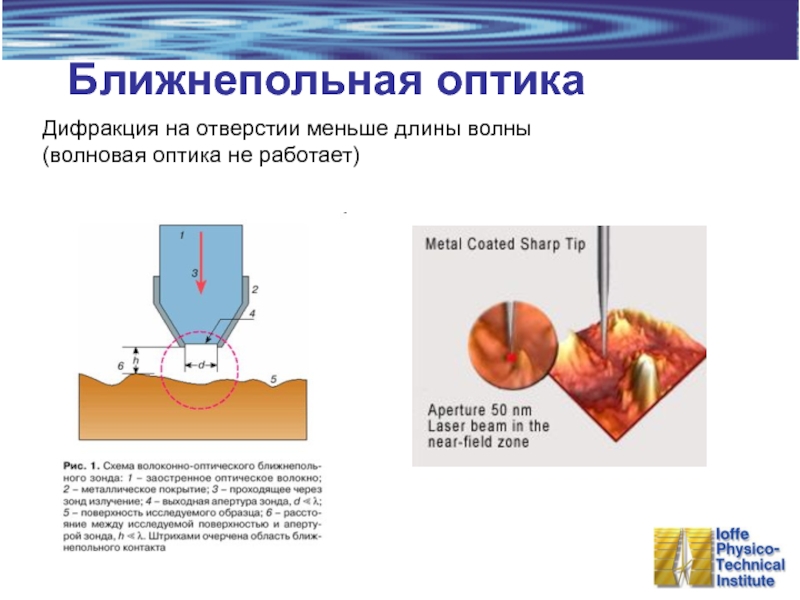
Слайд 18Ближнепольная оптика
Дифракция на отверстии меньше длины волны
(волновая оптика не работает)
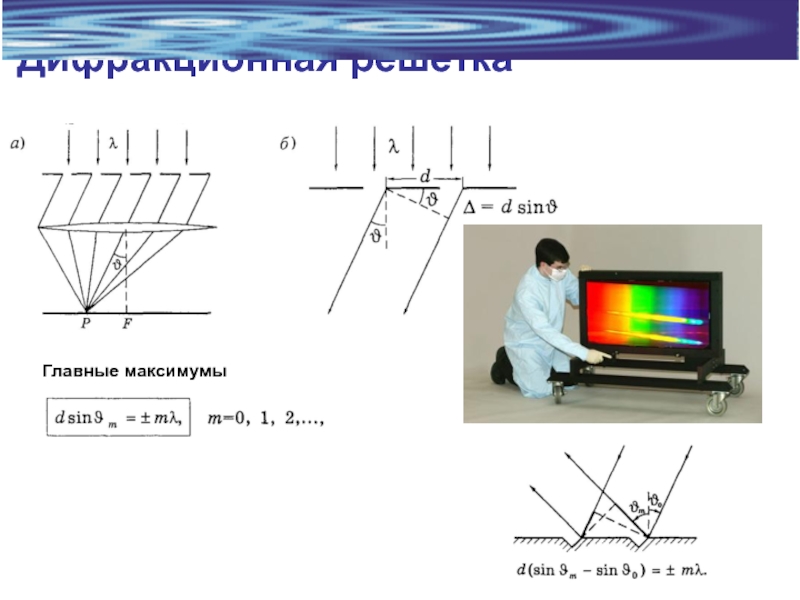
Слайд 20Дифракционная решетка
Условие минимумов
Угловая ширина
главных максимумов
Дифракционные минимумы
Слайд 22Фурье оптика
Гармонический анализ (Преобразование Фурье)
Представление произвольной функции f(t) (волнового фронта) в
Линейная система
Отклик системы на гармоническую функцию известен
Двумерное преобразование Фурье в пространственных координатах. Волны считаем монохроматическими.
ФУРЬЕ Жан Батист Жозеф
(1768-1830)
Слайд 23Фурье оптика
Плоские волны играют роль гармонических функций
Произвольная волна раскладывается по плоским
Линейная система характеризуются импульсным откликом и функцией пропускания (отклик на гармоническую функцию)
Слайд 24Свободное пространство
Параксиальном приближении
По распределению амплитуды можно определить волновые функции плоских волн
Слайд 27Зонная пластика Френеля
Зонная пластинка работает как сферическая линза со множеством фокусов
(высшие
В линзе Френеля используется квадратичная модуляция фазы
Слайд 28Передаточная функция
Линейная функция инвариантная к сдвигу системы координат
Свободное пространство
Плоские волны
Испытывают набег фазы при распространении, с более высокими частотами затухают
Детали с размерами менее длины волны не могут быть переданы линейной оптической системой на расстояние более длины волны (предел разрешения)
Произвольная оптическая система
Слайд 29Фурье преобразование
Одна плоская волна соответствует каждой точке
Нет вклада других волн из-за
Свободное пространство
Приближение Фраунгофера
Дифракция Фраунгофера