- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Квантовые эффекты в нелинейных системах презентация
Содержание
- 1. Квантовые эффекты в нелинейных системах
- 2. Туннельный переход S I S
- 3. Джозефсоновский переход
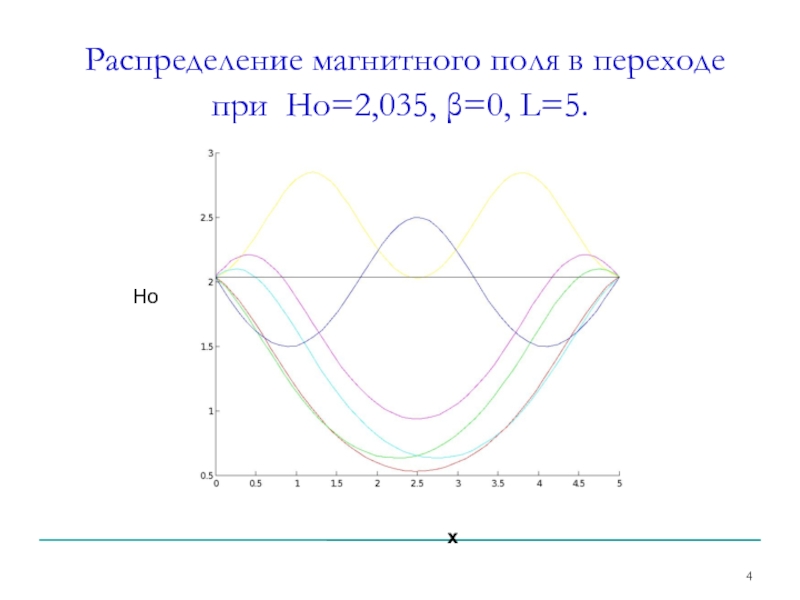
- 4. Распределение магнитного поля в переходе при Но=2,035, β=0, L=5. Но х
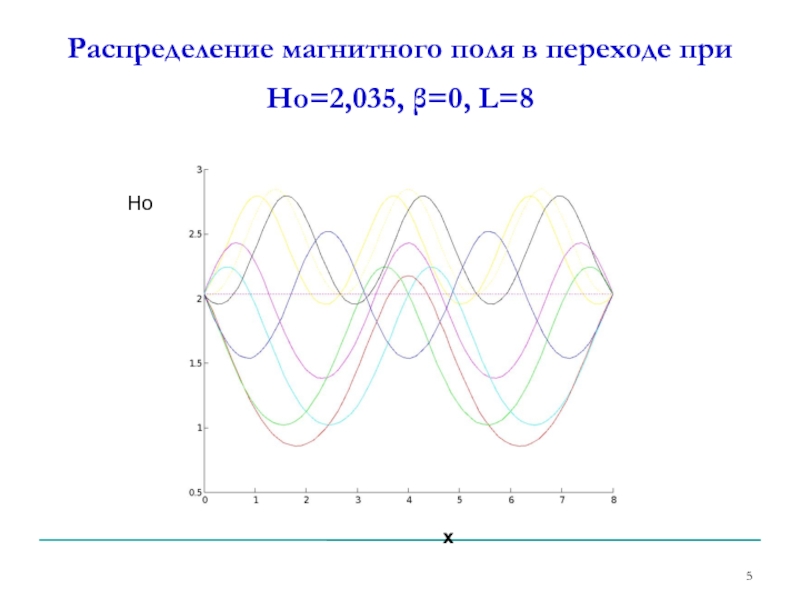
- 5. Распределение магнитного поля в переходе при Но=2,035, β=0, L=8 Но х
- 6. Распределение магнитного поля в переходе при Но=1,5, β=0, L=5
- 7. Распределение тока при Н0=1,174, β=0 и L=8 для мейсснеровского, однофлуксонного и двухфлуксонного состояний
- 8. Распределение магнитного поля при Н0=1,174, β=0 и L=8 для мейсснеровского, однофлуксонного и двухфлуксонного состояний
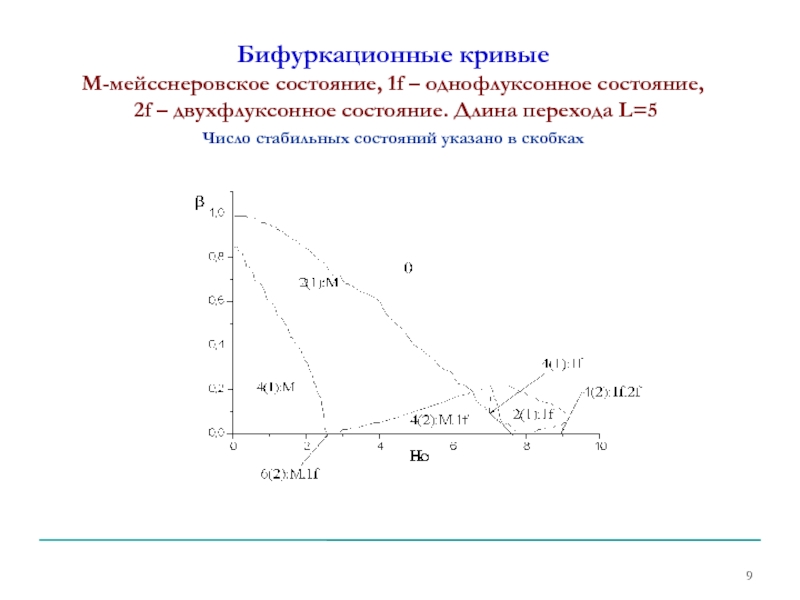
- 9. Бифуркационные кривые М-мейсснеровское состояние, 1f –
- 10. Асимптотические состояния и «эффект бабочки Брэдбери» Таблица 1.
- 11. Асимптотические состояния и «эффект бабочки Брэдбери»
- 12. Показатель Ляпунова Неустойчивость состояний определялась следующим образом:
- 13. Потенциал Гиббса и переходы между состояниями
- 14. Область сосуществования стационарных и нестационарных состояний и
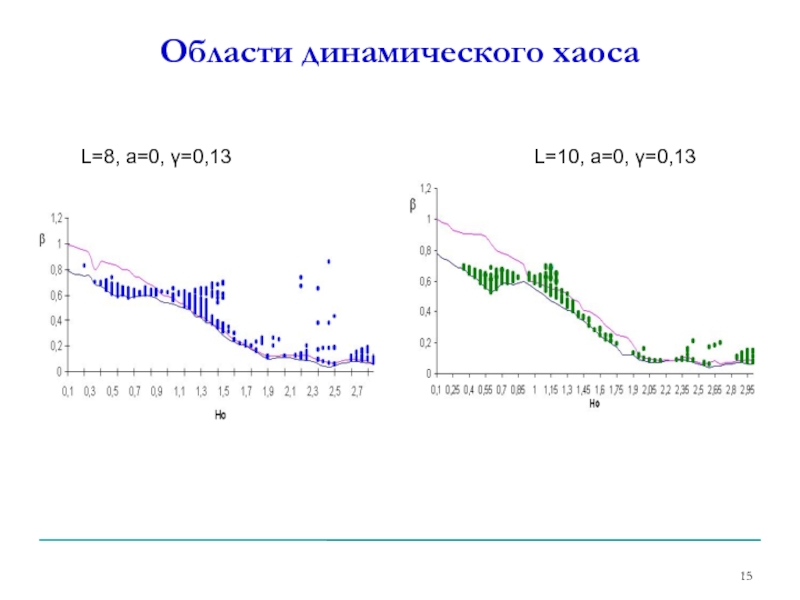
- 15. Области динамического хаоса L=8, а=0, γ=0,13 L=10, а=0, γ=0,13
- 16. Квантование потока в стационарных состояниях ϕ(х)|x→-∞
- 17. Квантование потока в стационарных состояниях Мейсснеровское состояние
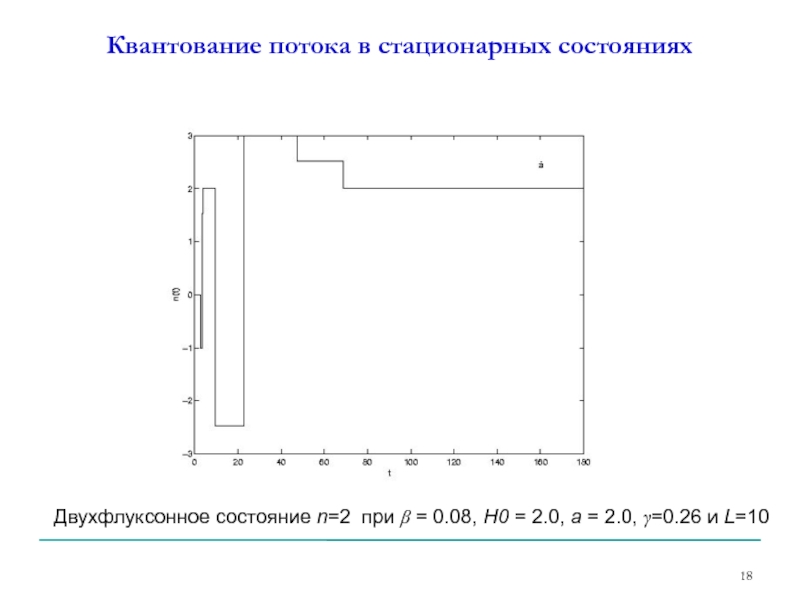
- 18. Квантование потока в стационарных состояниях Двухфлуксонное состояние
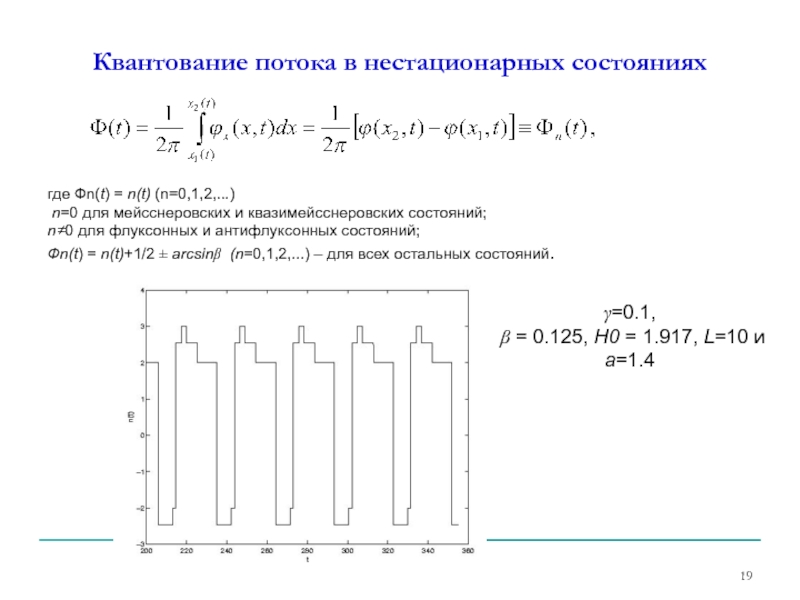
- 19. Квантование потока в нестационарных состояниях где
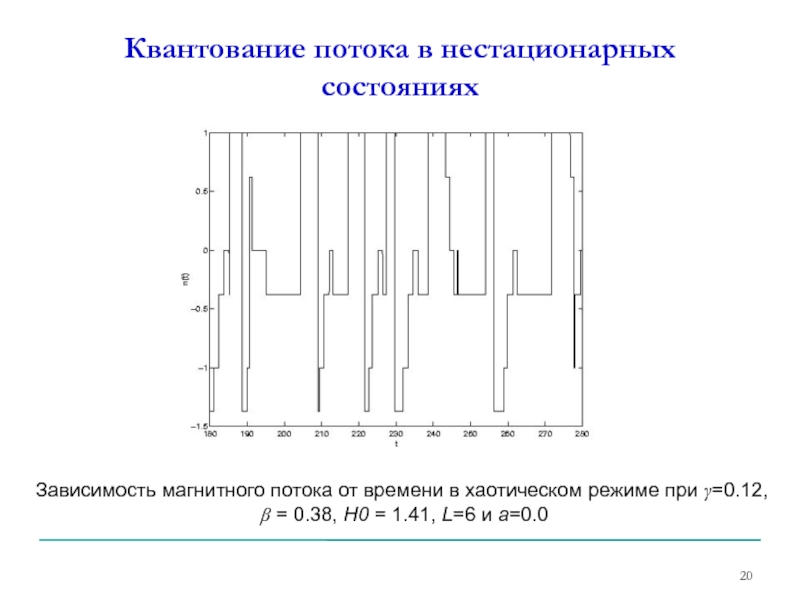
- 20. Квантование потока в нестационарных состояниях Зависимость магнитного
- 21. А. Эйнштейн: Я не
- 22. Литература Yugay K.N., et al. Phys.
- 23. Спасибо за внимание
Слайд 7Распределение тока при Н0=1,174, β=0 и L=8 для мейсснеровского, однофлуксонного
Слайд 8Распределение магнитного поля при Н0=1,174, β=0 и L=8 для мейсснеровского, однофлуксонного
Слайд 9Бифуркационные кривые М-мейсснеровское состояние, 1f – однофлуксонное состояние, 2f –
Слайд 12Показатель Ляпунова
Неустойчивость состояний определялась следующим образом:
нестационарное уравнение sin-Гордона линеаризовалось в окрестности
стационарного
возмущение. Уравнение для θ(x,t) – линеаризованное уравнение
sin-Гордона (1), решается затем с помощью разложения этой функции по
полной системе собственных функций оператора Шредингера с
потенциалом cos[ϕ(x)]:
где un(x) – собственные функции оператора Шредингера:
где γ - коэффициент диссипации в уравнении sin-Гордона. При λn < 0
решение ϕ(x) - устойчиво, а при λn > 0 оно неустойчиво.
Слайд 13Потенциал Гиббса и переходы между состояниями
Переходы между состояниями при H0=1,9; β=0;
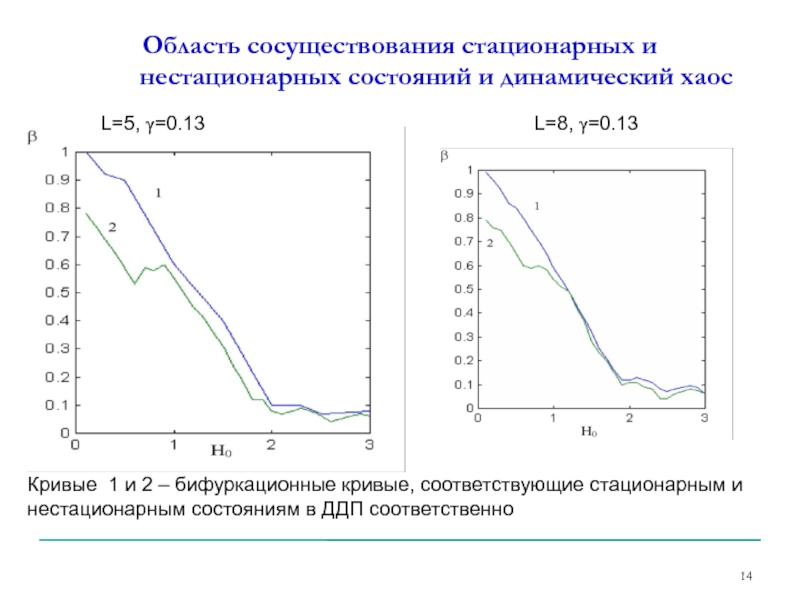
Слайд 14Область сосуществования стационарных и нестационарных состояний и динамический хаос
L=5, γ=0.13
L=8,
Кривые 1 и 2 – бифуркационные кривые, соответствующие стационарным и нестационарным состояниям в ДДП соответственно
Слайд 16Квантование потока в стационарных состояниях
ϕ(х)|x→-∞ = 0, ϕ(х)|x→+∞ = 2π
где Фn
n=0 для мейсснеровских и квазимейсснеровских состояний,
n>0 для флуксонных и антифлуксонных состояний ,
Фn = n+1/2 ± arcsinβ (n=0,1,2,...) – для всех остальных состояний
Теорема:
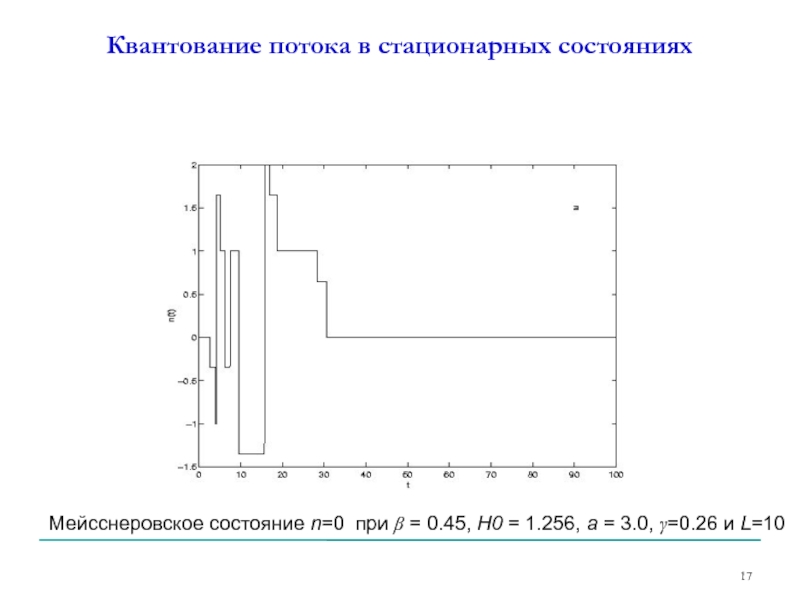
Слайд 17Квантование потока в стационарных состояниях
Мейсснеровское состояние n=0 при β = 0.45,
Слайд 18Квантование потока в стационарных состояниях
Двухфлуксонное состояние n=2 при β = 0.08,
Слайд 19Квантование потока в нестационарных состояниях
где Фn(t) = n(t) (n=0,1,2,...)
n≠0 для флуксонных и антифлуксонных состояний;
Фn(t) = n(t)+1/2 ± arcsinβ (n=0,1,2,...) – для всех остальных состояний.
γ=0.1,
β = 0.125, Н0 = 1.917, L=10 и а=1.4
Слайд 20Квантование потока в нестационарных состояниях
Зависимость магнитного потока от времени в хаотическом
β = 0.38, Н0 = 1.41, L=6 и а=0.0
Слайд 22Литература
Yugay K.N., et al. Phys. Rev. B, 49, 12036 (1994).
Yugay K.N.,
Н.В.Блинов, И.В.Широков, К.Н.Югай. Вестник Омского универ., №2, 29 (1998).
Yugay K.N., et al. Low Temp. Phys., 25, 530 (1999).
Yugay K.N., et al. Low Temp. Phys., 26, 1067 (2000).
Югай К.Н., et al. Известия вузов. Прикладная и нелинейная динамика, 9, 51 (2001).
Югай К.Н., et al. Вестник Омского универ., №2, 22 (2001).
Yugay K.N. et al. JKPS, 46, 1418 (2005).
Yugay K.N. et al. J. Superconductivity Nov. Magn., 19, 135 (2006).