В.И.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Критичность ограниченных размножающих сред презентация
Содержание
- 1. Критичность ограниченных размножающих сред
- 2. Одногрупповое диффузионное приближение Для выяснения
- 3. Одногрупповое диффузионное приближение В отсутствии в
- 4. Одногрупповое диффузионное приближение Для стационарного случая
- 5. Одногрупповое диффузионное приближение Разлагая Ф(r) вблизи
- 6. Одногрупповое диффузионное приближение
- 7. Одногрупповое диффузионное приближение общая постановка задачи
- 8. Одногрупповое диффузионное приближение
- 9. Одногрупповое диффузионное приближение Наименьшему собственному значению
- 10. Одногрупповое диффузионное приближение Функция пространственного
- 11. Сферический реактор В сферически симметричном случае лапласиан
- 12. Сферический реактор Общее решение этого уравнения
- 13. Сферический реактор Критический радиус активной зоны
- 14. Сферический реактор
- 15. Цилиндрический реактор Рассмотрим цилиндрическую активную зону радиуса
- 16. Цилиндрический реактор Метод разделения переменных
- 17. Цилиндрический реактор Общее решение уравнений с учетом
- 18. Цилиндрический реактор геометрический параметр для цилиндрической активной
- 19. Цилиндрический реактор Рассмотрим частный случай
- 20. Цилиндрический реактор Из условия критичности для цилиндра
- 21. Цилиндрический реактор используя ограничение, выразим одну
- 22. Сферический реактор Рассмотрим влияние плотности размножающей среды
- 23. Сферический реактор Изменится величина длины
- 24. Эффективный коэффициент размножения Для ограниченных размножающих
- 25. Эффективный коэффициент размножения Для сохранения баланса
- 26. Эффективный коэффициент размножения Запишем условие критичности
- 27. Эффективный коэффициент размножения проинтегрируем уравнение условно-критического
- 28. Эффективный коэффициент размножения
- 29. Эффективный коэффициент размножения в активной зоне
Слайд 1Критичность ограниченных размножающих сред
кафедра
«Теоретическая и экспериментальная физика ядерных реакторов»
доцент
Савандер
Слайд 2Одногрупповое диффузионное приближение
Для выяснения чисто пространственных эффектов в конечных
размножающих средах введем ряд упрощающих предположений:
Рассматривается однородная размножающая среда, занимающая некоторый объем V;
Пренебрегаем энергетической зависимостью потока нейтронов (одногрупповое приближение)
Для учета углового распределения нейтронов рассмотрим функцию полного потока и полного тока нейтронов (P1 –приближение)
Рассматривается однородная размножающая среда, занимающая некоторый объем V;
Пренебрегаем энергетической зависимостью потока нейтронов (одногрупповое приближение)
Для учета углового распределения нейтронов рассмотрим функцию полного потока и полного тока нейтронов (P1 –приближение)
Слайд 3Одногрупповое диффузионное приближение
В отсутствии в размножающей среде сильных локальных поглотителей
и для областей активной зоны, удаленных от границы реактора с пустотой связь между этими величинами дается законом Фика:
Одногрупповое диффузионное приближение
Одногрупповое диффузионное приближение
Слайд 4Одногрупповое диффузионное приближение
Для стационарного случая
Рассмотрим простейший случай так называемого
«голого» реактора, когда размножающая среда граничит с вакуумом.
В одногрупповом диффузионном приближении точное граничное условие заменяется приближенным
В одногрупповом диффузионном приближении точное граничное условие заменяется приближенным
Слайд 5Одногрупповое диффузионное приближение
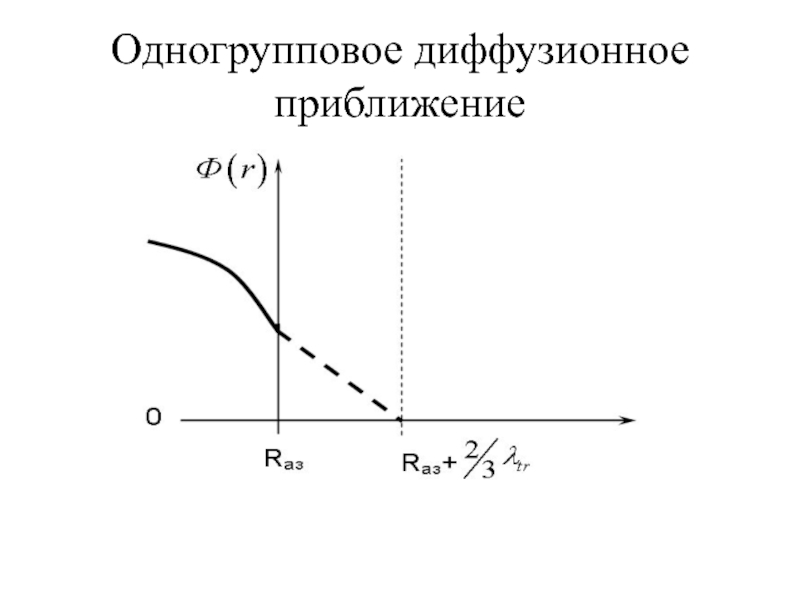
Разлагая Ф(r) вблизи границы с вакуумом в ряд
до линейного члена, получим:
Если теперь экстраполировать распределение нейтронов за пределы среды в пустоту, то экстраполированный поток нейтронов обратится в нуль на расстоянии
от геометрической границы реактора. Эта величина называется экстраполированной добавкой среды
Если теперь экстраполировать распределение нейтронов за пределы среды в пустоту, то экстраполированный поток нейтронов обратится в нуль на расстоянии
от геометрической границы реактора. Эта величина называется экстраполированной добавкой среды
Слайд 7Одногрупповое диффузионное приближение
общая постановка задачи в одногрупповом диффузионном приближении такова:
требуется найти ограниченное положительное решение задачи:
Введем следующие обозначения:
Введем следующие обозначения:
Слайд 8Одногрупповое диффузионное приближение
материальный параметр среды
- длина диффузии нейтронов в размножающей среде
Это задача на определение собственных чисел и собственных функций оператора Лапласа
- длина диффузии нейтронов в размножающей среде
Это задача на определение собственных чисел и собственных функций оператора Лапласа
Слайд 9Одногрупповое диффузионное приближение
Наименьшему собственному значению соответствует знакопостоянная собственная функция
Стационарное решение
будет только в том случае
Величина (α0)2 - геометрический параметр определяется геометрией объема среды.
Величина (α0)2 - геометрический параметр определяется геометрией объема среды.
Слайд 10Одногрупповое диффузионное приближение
Функция пространственного распределения потока нейтронов
условие критичности
реактора и означает, что для размножающей среды заданной геометрической формы существуют такие размеры, при которых в этой среде возможен стационарный процесс размножения нейтронов (деления ядер). Соответствующие размеры такой среды называются критическими размерами, а отвечающий этим размерам объем мультиплицирующей среды – критическим объемом. Масса делящегося вещества в такой среде называется критической массой.
Слайд 11Сферический реактор
В сферически симметричном случае лапласиан имеет вид:
геометрический параметр определяется из
решения волнового уравнения:
Слайд 12Сферический реактор
Общее решение этого уравнения
Условие ограниченности решения задачи
Граничное условие
Условие критичности
Слайд 13Сферический реактор
Критический радиус активной зоны
Константа C определяется из условия нормировки на
мощность
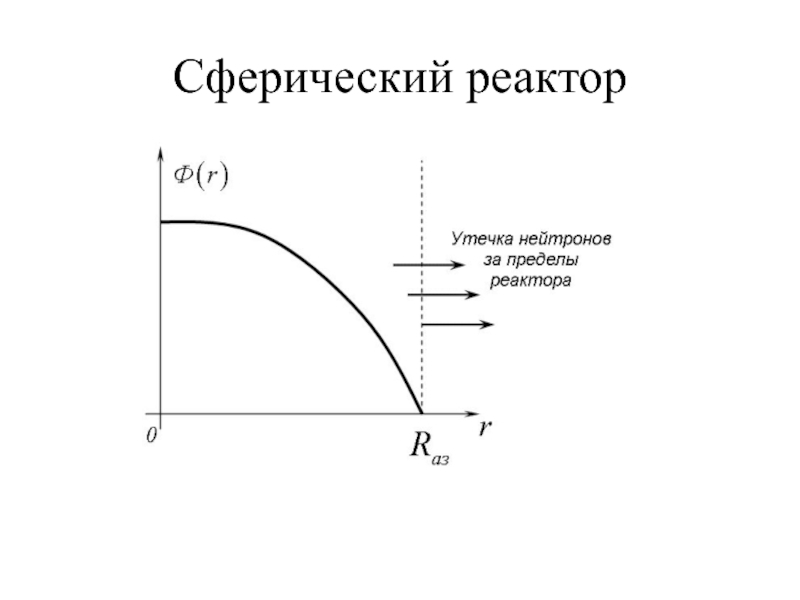
Пространственное распределение потока нейтронов характеризуется спадом потока нейтронов к границе реактора, поскольку через границу реактора происходит утечка нейтронов в вакуум
Пространственное распределение потока нейтронов характеризуется спадом потока нейтронов к границе реактора, поскольку через границу реактора происходит утечка нейтронов в вакуум
Слайд 15Цилиндрический реактор
Рассмотрим цилиндрическую активную зону радиуса R и высоты H
Задача
на определение геомет-
рического параметра
рического параметра
Слайд 17Цилиндрический реактор
Общее решение уравнений с учетом ограниченности потока нейтронов
Из краевых условий
Слайд 18Цилиндрический реактор
геометрический параметр для цилиндрической активной зоны и распределение плотности потока
нейтронов в реакторе:
Условие критичности
Условие критичности
Слайд 19Цилиндрический реактор
Рассмотрим частный случай
то критичность реактора достигается при
бесконечной высоте . Для тех цилиндров, радиус которых меньше R, критичность не достигается ни при каком значении высоты цилиндра.
Eсли высоту цилиндра взять из условия
то критичность такого реактора достигается только при бесконечно большом радиусе цилиндра. Если высота активной зоны меньше H, то реактор при любом радиусе будет подкритичным. Это примеры некритических объемов.
Eсли высоту цилиндра взять из условия
то критичность такого реактора достигается только при бесконечно большом радиусе цилиндра. Если высота активной зоны меньше H, то реактор при любом радиусе будет подкритичным. Это примеры некритических объемов.
Слайд 20Цилиндрический реактор
Из условия критичности для цилиндра следует, что при заданном материальном
параметре размножающей среды получается бесконечное множество критических активных зон. Среди них есть такой цилиндр, у которого минимальный объем.
Постановка задачи: найти минимум функции двух переменных с учетом условия связи между переменными
Постановка задачи: найти минимум функции двух переменных с учетом условия связи между переменными
Слайд 21Цилиндрический реактор
используя ограничение, выразим одну из переменных через другую
Условие
экстремальности критического объема
находим радиус и высоту оптимального цилиндра:
находим радиус и высоту оптимального цилиндра:
Слайд 22Сферический реактор
Рассмотрим влияние плотности размножающей среды на критичность реактора. Критический радиус
и критический объем сферы
Предположим, что плотность размножающей среды изменилась, а соотношение топлива и замедлителя осталось неизменным
коэффициент размножения при этом не должен измениться
Предположим, что плотность размножающей среды изменилась, а соотношение топлива и замедлителя осталось неизменным
коэффициент размножения при этом не должен измениться
Слайд 23Сферический реактор
Изменится величина длины диффузии
Таким образом
а
Учитывая, что ρ~γ , получим Мкр~1/ γ2 .
Так, например, если плотность ядерного материала увеличить в два раза, то критическая масса уменьшится в четыре раза
Учитывая, что ρ~γ , получим Мкр~1/ γ2 .
Так, например, если плотность ядерного материала увеличить в два раза, то критическая масса уменьшится в четыре раза
Слайд 24Эффективный коэффициент размножения
Для ограниченных размножающих сред также можно ввести понятие
коэффициента размножения, так называемый эффективный коэффициент размножения .
Рассмотрим некритическую среду. Некритичность связана с тем, что нарушен баланс между числом генерируемых реакцией деления нейтронов
и поглощением и утечкой нейтронов из активной зоны .
Рассмотрим некритическую среду. Некритичность связана с тем, что нарушен баланс между числом генерируемых реакцией деления нейтронов
и поглощением и утечкой нейтронов из активной зоны .
Слайд 25Эффективный коэффициент размножения
Для сохранения баланса разделим источник нейтронов на некоторое
число Кэф. Для критического реактора Кэф=1. Для подкритического Кэф<1, а для надкритического Кэф>1.
Такой реактор называется условно критическим
Такой реактор называется условно критическим
Слайд 26Эффективный коэффициент размножения
Запишем условие критичности для этого реактора
эффективный коэффициент размножения
учитывает не только размножающие свойства среды, но и форму, и размеры активной зоны реактора.
Для бесконечного реактора
Для бесконечного реактора
Слайд 27Эффективный коэффициент размножения
проинтегрируем уравнение условно-критического реактора по объему активной зоны
где
I - утечка нейтронов из реактора, равная числу нейтронов, покидающих активную зону реактора в единицу времени:
-скорость поглощения, равная числу нейтронов, поглощенных в активной зоне в единицу времени
-скорость поглощения, равная числу нейтронов, поглощенных в активной зоне в единицу времени
Слайд 28Эффективный коэффициент размножения
- скорость генерации нейтронов
Из этого баланса выразим эффективный коэффициент размножения:
где а вероятность нейтрону,
рожденному в активной зоне, поглотится в ней.
Из этого баланса выразим эффективный коэффициент размножения:
где а вероятность нейтрону,
рожденному в активной зоне, поглотится в ней.
Слайд 29Эффективный коэффициент размножения
в активной зоне условно-критического реактора, в котором ,
скорость рождения нейтронов равно скорости поглощения и утечки нейтронов Кэф=1
В общем случае
В общем случае