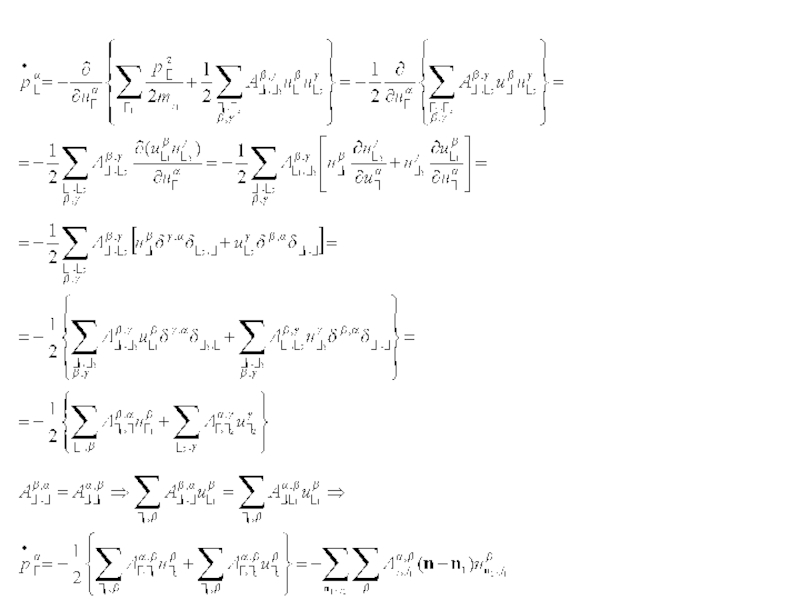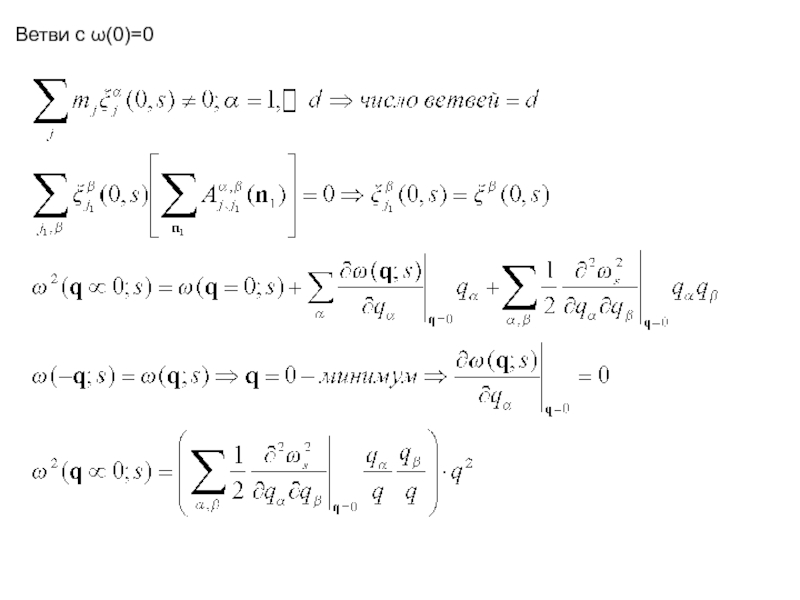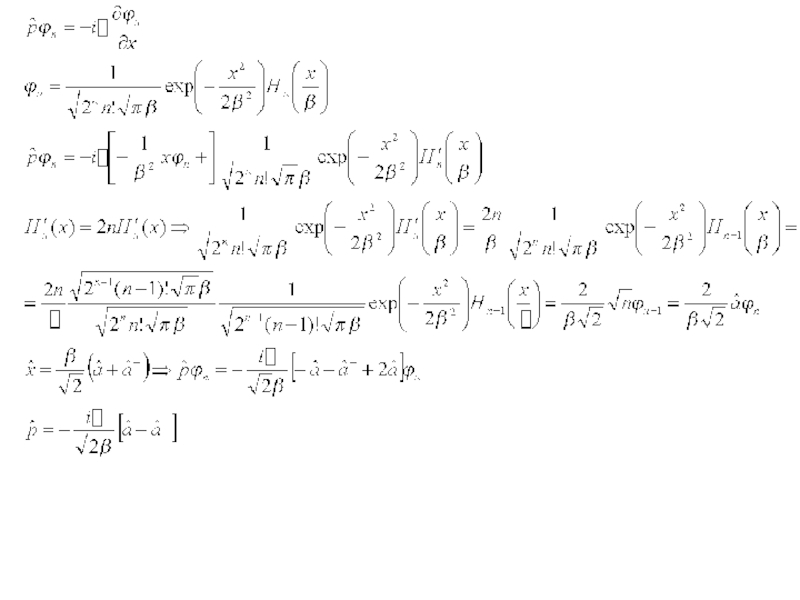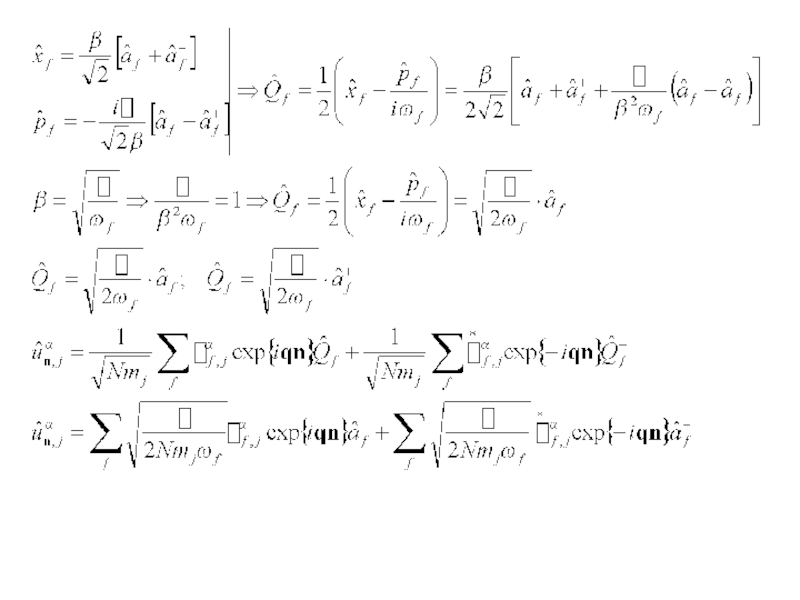Колебания кристаллической решетки презентация

под мгновенное положение ядер (атомных остовов)=>движение ядер можно рассматривать в эффективном среднем поле, создаваемом электронами (рассчитывается в предположении неподвижных ядер)




Амплитуда смещения атомов << расстояния между ними => потенциальную энергию кристаллической решетки можно разложить в ряд Тейлора в окрестности равновесных положений атомов

- Константа для данного кристалла (берем за начало отсчета энергии)

проекция на ось силы, действующей в положении равновесия на i-ый атом со стороны всех остальных

ЛГО

Переходим к нормальным координатам (обязательно при этом учитывая периодичность расположения положений равновесия атомов)

- ЛГО с единичной массой и частотой, равной частоте нормального колебания

того, чтобы задать стационарное состояние всей системы осцилляторов нужно указать число заполнения каждого осциллятора.

Каждому осциллятору (собственному колебанию) поставим в соответствие квазичастицу с энергией, равной кванту этого осциллятора. Такие квазичастицы называются фононами. Поставим нашей системе осцилляторов газ таких фононов так, чтобы число фононов данного типа в газе равнялось числу заполнения соответствующего осциллятора. Если система осцилляторов переходит из одного состояния в другое, т.е. меняются числа заполнения осцилляторов, то соответствующее число фононов рождается и исчезает.

с газом частиц => удобно перейти в представление вторичного квантования. Введем операторы уничтожения и рождения фононов

В этом можно формально убедиться, вычислив стат. сумму системы осцилляторов.

случае, когда потенциальная энергия имеет вид потенциальной ямы. Положение равновесия системы есть минимум ее потенциальной энергии.

силовые коэффициенты (характеризуют действующие на атомы силы, которые возникают при их отклонении от положения равновесия

и ее первые производные – непрерывные => вторые производные U не зависят от порядка дифференцирования

В основном объеме все элементарные ячейки - физически эквивалентны. => Энергия взаимодействия между атомами может зависеть только от положения их в ячейке и от относительного положения ячеек, в которых они находятся, но не от положений ячеек по отдельности.

Кристалл – периодическая структура => при параллельном переносе или при повороте решетки как целого не возникает действующих на атомы дополнительных сил

решение – линейная комбинация гармонических решений (плоских волн). Число плоских волн (фундаментальных решений) = число уравнений = dgN.
Произвольное колебание кристаллической решетки

- Собственное колебание

- квазиволновой вектор (определяет направление распространения волны)

номер ветви (нумерует собственные колебания с одинаковым q).

q соответствует dg собственных колебаний.

Груперуем собственные колебания по порядку возростания частоты

Совокупность всех собственных колебаний с данным s – s-я ветвь собственных колебаний. Всего ветвей dg

вещественные (можно показать, что сами частоты неорицательны)

Из линейно независимых собственных векторов эрмитовой матрицы можно сформировать полную ортонормированную систему => амплитуды собственных колебаний с данным волновым вектором образуют ПОНС

- условие ортогональности

- условие полноты

Бриллюэна

- Непрерывная функция в первой зоне Бриллюэна => ограниченная

граничные условия призваны отражать физическую картину на границе кристалла, как правило очень сложную.

Решение: Силы быстро убывают с расстоянием => в глубине кристалла граница не ощущается => в объемных кристаллах можно срезать приграничную область, и рассматривать только внутренний объем, в котором влиянием границы можно пренебречь.

Внутренний объем разбиваем на одинаковые макроскопические параллелепипеды, построенные на векторах элементарных трансляций.

Кристалл – периодическая структура => Все параллелепипеды – физически эквивалентны => разумно потребовать, чтобы

Физическая эквивалентность параллелепипеда (в среднем все одинаково) => достаточно рассмотреть только один параллелепипед с граничными условиями

различных значений квазиволнового вектора?

Выбор зоны Бриллюэна – вопрос удобства. Возьмем в качестве зоны Бриллюэна параллелепипед, построенный на векторах элементарных трансляций обратной решетки

Число физически различных значений квазиволнового вектора=число элементарных ячеек.

Число различных собственных колебаний – утроенное число атомов

qa<<1)

скорость звука

в колебаниях акустических ветвей при длинных волнах все атомы в элементарной ячейке смещаются практически одинаково, т.е. элементарная ячейка колеблется как целое. Длинные волны – накрывают много ячеек => замыватся дискретность среды => получаются эффективно волны в сплошной среде - звук

ветвей c

в колебаниях оптических ветвей при длинных волнах положение центра тяжести элементарной ячейки практически не меняется, т.е. ячейка деформируется

гармоническому закону => нормальные координаты

акустические фононы)

В знаменателе подынтегрального выражения стоит экспонента => основной вклад в ET дают колебания с частотой

При каких температурах этому условию удовлетворяют только звуковые колебания акустических ветвей?

- При этих температурах можно учитывать только вклад звуковых колебаний акустических ветвей

- усредняем скорость звука

дисперсии акустических ветвей и распространять интегрирование на все q-пространство (основной вклад дают звуковые колебания => ошибка мала)

Обезразмеривающая замена переменной

разложение в ряд Тейлора

Дюлонга-Пти

собственных колебаний с частотой в интервале
ω0- ω 0+Δ ω

- плотность собственных колебаний

- Число собственных колебаний с частотой в физ. беск. малом интерв

в плотности колебаний отражается на измеряемых величинах