- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Классификация связей в динамике презентация
Содержание
- 1. Классификация связей в динамике
- 2. Рассмотреть классификацию связей в динамике, познакомиться с
- 3. В статике: Связи - то, что не
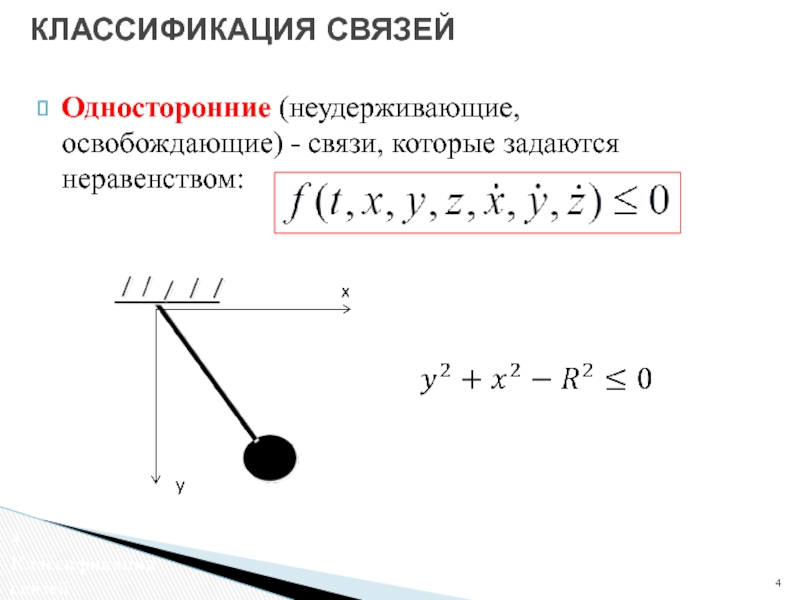
- 4. Односторонние (неудерживающие, освобождающие) - связи, которые задаются неравенством: КЛАССИФИКАЦИЯ СВЯЗЕЙ Классификация связей
- 5. Двусторонние (удерживающие, неосвобождающие) – связи, которые задаются уравнением: КЛАССИФИКАЦИЯ СВЯЗЕЙ Классификация связей
- 6. Стационарные связи - связи, уравнения которых не
- 7. Нестационарные связи - связи, уравнения которых содержат
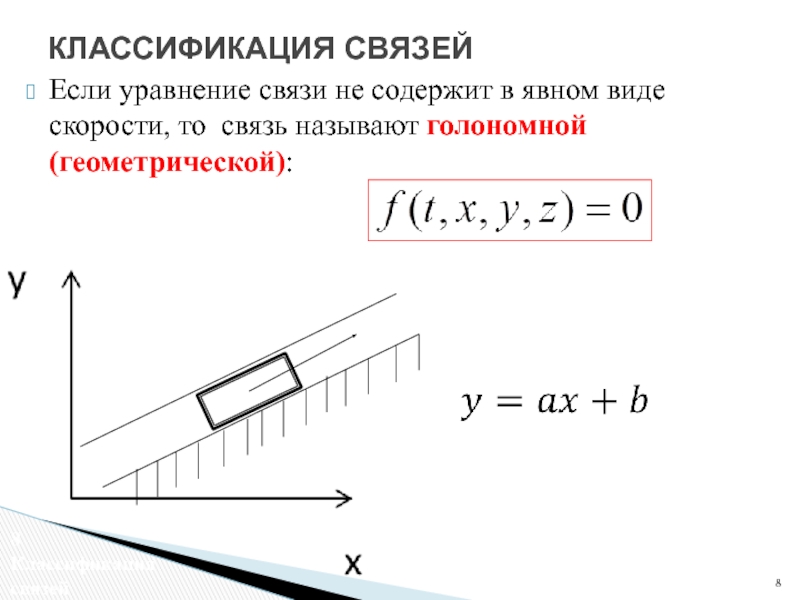
- 8. Если уравнение связи не содержит в явном
- 9. Если уравнение связи содержит в явном виде
- 10. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ Принцип возможных перемещений
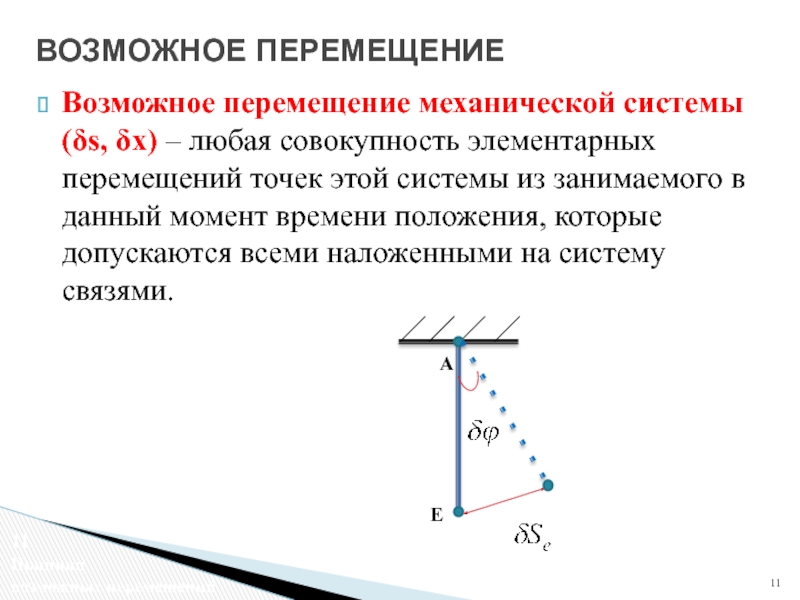
- 11. Возможное перемещение механической системы (δs, δx) –
- 12. Возможные перемещения характеризуются тем, что они: могут
- 13. Возможная работа – это элементарная работа, которую
- 14. Устанавливает общее условие равновесия механической системы в
- 15. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ Для равновесия механической
- 16. Необходимость: Пусть механическая система находится под действием
- 17. Достаточность: Пусть механическая система с идеальными
- 18. Пример: Найти величину силы Р, удерживающей тяжелые
- 19. Принцип возможных перемещений позволяет решать самые разнообразные
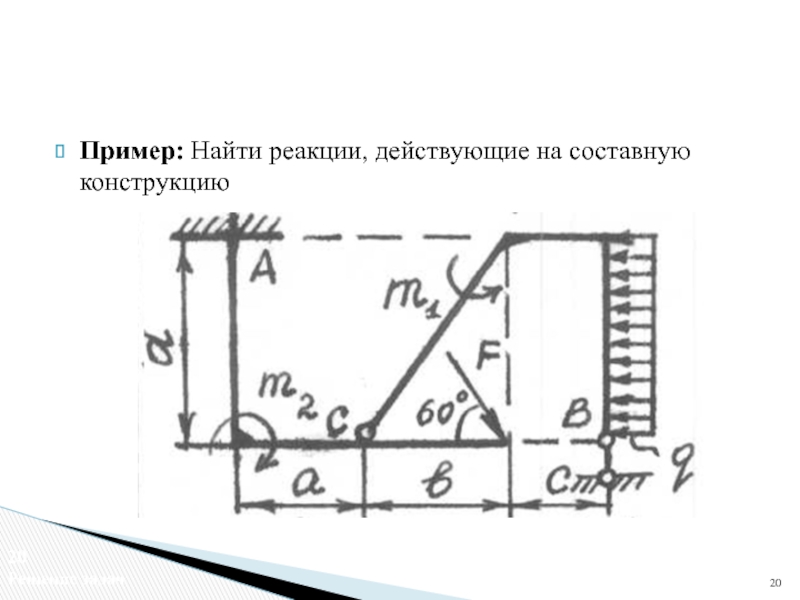
- 20. Пример: Найти реакции, действующие на составную конструкцию Решение задач
Слайд 1 Классификация связей.
Принцип возможных перемещений.
ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ.
ДИНАМИКА
Слайд 2Рассмотреть классификацию связей в динамике, познакомиться с принципом возможных перемещений и
ПЛАН ЛЕКЦИИ
Классификация связей;
Принцип возможных перемещений;
Решение задач;
Заключение.
ЦЕЛЬ ЛЕКЦИИ
2
Слайд 3В статике:
Связи - то, что не даёт перемещаться
Действие связей описывается реакциями.
В
Связи - любого вида ограничения, которые налагаются на положение и скорость движущихся тел (точек).
Действие связи описывается уравнениями (или неравенствами), которые определяют ограничения на движение тел.
СВЯЗИ
Классификация связей
Слайд 4Односторонние (неудерживающие, освобождающие) - связи, которые задаются неравенством:
КЛАССИФИКАЦИЯ СВЯЗЕЙ
Классификация связей
Слайд 5Двусторонние (удерживающие, неосвобождающие) – связи, которые задаются уравнением:
КЛАССИФИКАЦИЯ СВЯЗЕЙ
Классификация связей
Слайд 6Стационарные связи - связи, уравнения которых не содержат времени в явном
КЛАССИФИКАЦИЯ СВЯЗЕЙ
Классификация связей
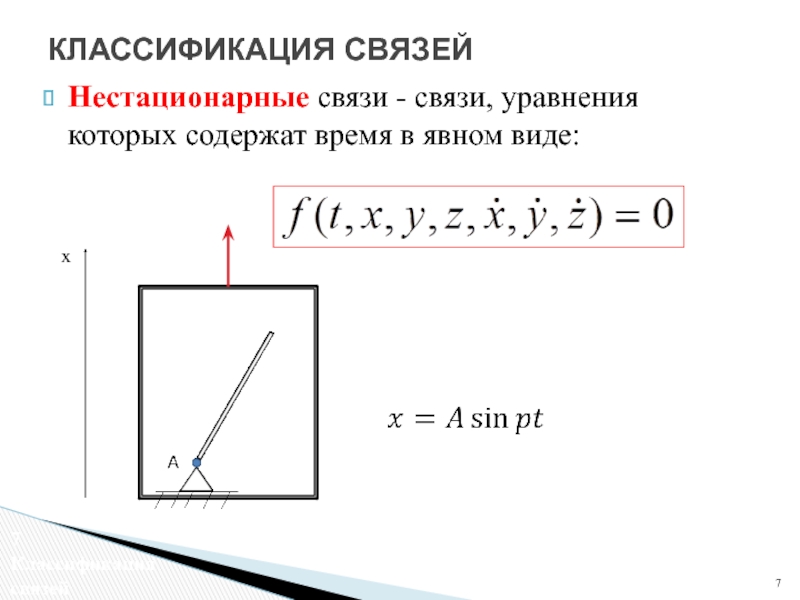
Слайд 7Нестационарные связи - связи, уравнения которых содержат время в явном виде:
КЛАССИФИКАЦИЯ СВЯЗЕЙ
x
Классификация связей
Слайд 8Если уравнение связи не содержит в явном виде скорости, то связь
КЛАССИФИКАЦИЯ СВЯЗЕЙ
Классификация связей
Слайд 9Если уравнение связи содержит в явном виде скорость, то связь называют
КЛАССИФИКАЦИЯ СВЯЗЕЙ
A
Классификация связей
Слайд 11Возможное перемещение механической системы (δs, δx) – любая совокупность элементарных перемещений
ВОЗМОЖНОЕ ПЕРЕМЕЩЕНИЕ
А
Е
Принцип
возможных перемещений
Слайд 12Возможные перемещения характеризуются тем, что они:
могут и не происходить (они воображаемые);
бесконечно
происходят с сохранением всех наложенных на систему связей;
не связаны с реальным времененм (δt = 0).
Для стационарных связей действительное перемещение dr можно представить как набор возможных
ВОЗМОЖНОЕ ПЕРЕМЕЩЕНИЕ
Принцип
возможных перемещений
Слайд 13Возможная работа – это элементарная работа, которую действующая на материальную точку
Связи, сумма возможных работ реакций которых на любом возможном перемещении равна нулю, называются идеальными связями :
ВОЗМОЖНАЯ РАБОТА
Принцип
возможных перемещений
Слайд 14Устанавливает общее условие равновесия механической системы в целом
При идеальных связях
Выполняется в инерциальных системах отсчета
ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
Принцип
возможных перемещений
Слайд 15
ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
Для равновесия механической системы с идеальными связями необходимо и
Принцип
возможных перемещений
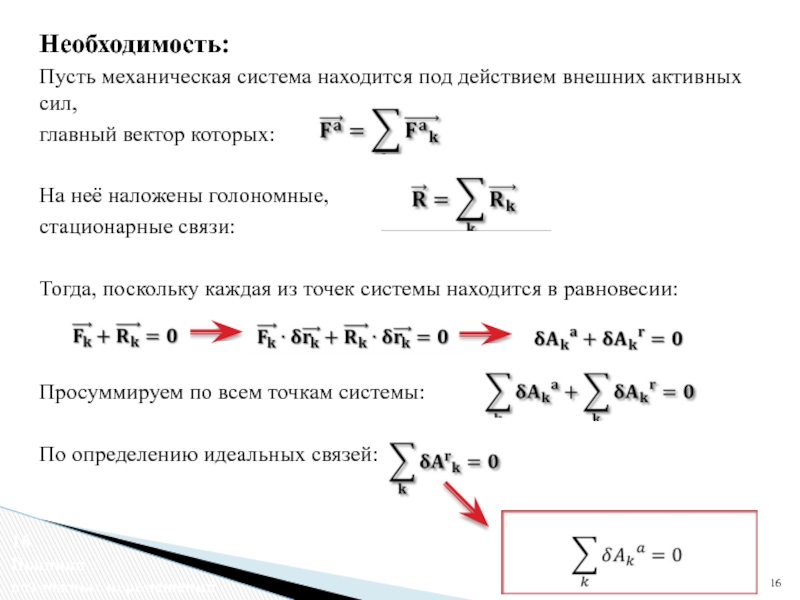
Слайд 16Необходимость:
Пусть механическая система находится под действием внешних активных сил,
главный вектор которых:
На неё наложены голономные,
стационарные связи:
Тогда, поскольку каждая из точек системы находится в равновесии:
Просуммируем по всем точкам системы:
По определению идеальных связей:
Принцип
возможных перемещений
Слайд 17Достаточность:
Пусть механическая система с идеальными связями, удовлетворяющая неравенству
совершает действительное перемещение
Тогда: dT =
При стационарных связях действительные перемещения совпадают с какими-либо возможными перемещениями:
Но это противоречит условию:
Когда приложенные силы к системе удовлетворяют этому условию, система из состояния покоя выйти не может, следовательно, это условие является достаточным условием равновесия системы.
Принцип
возможных перемещений
Слайд 18Пример: Найти величину силы Р, удерживающей тяжелые гладкие призмы с массами m1 m2 в состоянии
РЕШЕНИЕ ЗАДАЧ
Решение задач
Слайд 19Принцип возможных перемещений позволяет решать самые разнообразные задачи на равновесие механических
Решение задач