- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Кинетика химических реакций презентация
Содержание
- 1. Кинетика химических реакций
- 2. Основоположники химической кинетики Якоб Хендрик Вант-Гофф (нидерл.
- 3. Э́ЙРИНГ (Eyring) Генри (1901-1981), американский физикохимик. Область
- 4. Введение в кинетику Стехиометрия.
- 6. В бимолекулярной реакции взаимодействуют
- 7. Кинетическое уравнение Рассмотрим
- 8. ; Скорость реакции равна скорости
- 9. Порядок реакции
- 10. Константа скорости
- 11. Кинетические уравнения первого порядка
- 12. Определение константы
- 13. Метод подстановки
- 15. Кинетические уравнения второго порядка
- 16. Подстановка const в
- 17. Метод подстановки
- 19. Кинетические уравнения третьего порядка
- 21. Кинетика сложных реакций Большинство
- 22. Пусть а —
- 23. Интегрирование кинетического уравнения
- 24. Последовательные реакции
- 26. При интегрировании полученного дифференциального уравнения при начальных
- 27. Параллельные реакции
- 28. Дифференциальные уравнения для
- 29. Таким образом, для
- 31. Представляют интерес цепные реакции в некоторых важнейших
- 32. Метод стационарных концентраций Для
- 33. Запишем дифференциальное кинетическое уравнение по интермедиату: Запишем
Слайд 1Кинетика химических реакций
Химическая кинетика – это учение о химическом процессе, его
Химическая кинетика устанавливает:
временные закономерности протекания химических реакций;
связь между скоростью реакции и условиями ее проведения;
выявляет факторы, влияющие на скорость и направление химических реакций.
Важнейшая задача химической кинетики: выяснение механизма химических превращений, взаимосвязи между скоростью химической реакции и строением молекул реагирующих веществ; изучение элементарных реакций с участием активных частиц: свободных атомов и радикалов, ионов и ион – радикалов, возбужденных молекул и др.
Слайд 2Основоположники химической кинетики
Якоб Хендрик Вант-Гофф (нидерл. Jacobus Henricus (Henry) van 't
Сва́нте А́вгуст Арре́ниус (1859—1927, имение Вейк) — выдающийся шведский физико-химик и астрофизик, лауреат Нобелевской премии по химии (1903).
Слайд 3Э́ЙРИНГ (Eyring) Генри (1901-1981), американский физикохимик. Область изучения - квантовая химиия
ПОЛЯНИ (Polanyi) Майкл
(1891 - 1976 ). Основные работы посвящены физической химии, прежде всего химической кинетике и изучению кристаллических структур.
Слайд 4Введение в кинетику
Стехиометрия.
Нельзя считать, что стехиометрическое уравнение обязательно отражает механизм молекулярного процесса между реагентами. Стехиометрическое уравнение для производства аммиака по Габеру имеет вид:
N2 + 3H2 =2NH3 ,
но это вовсе не означает, что три молекулы водорода и одна азота, одновременно сталкиваясь, дают две молекулы аммиака.
Слайд 5
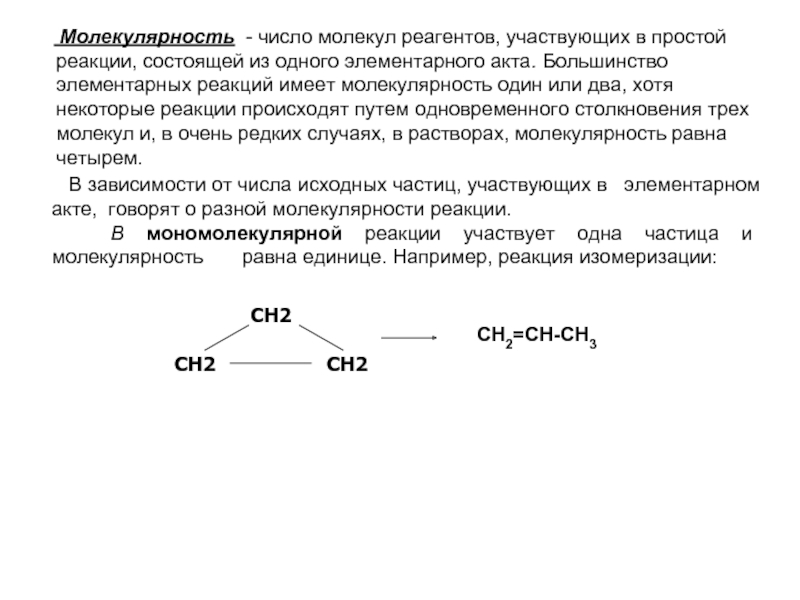
Молекулярность - число молекул реагентов,
В зависимости от числа исходных частиц, участвующих в элементарном акте, говорят о разной молекулярности реакции.
В мономолекулярной реакции участвует одна частица и молекулярность равна единице. Например, реакция изомеризации:
СН2
СН2 СН2
СН2=СН-СН3
Слайд 6 В бимолекулярной реакции взаимодействуют две одинаковые или неодинаковые
СН2=СН2+HI →CH3-CH2-I
В тримолекулрной реакции одновременно происходит столкновение трех молекул с образованием продукта. Такие реакции встречаются крайне редко. Молекулярность равна трем.
H·+ H·+ Ar , H2+Ar
Слайд 7Кинетическое уравнение
Рассмотрим химическую реакцию разложения реагента A
А В + С
В процессе реакции концентрация реагента А уменьшается, а продуктов В и С — возрастает. Скорость реакции в момент времени t задается тангенсом угла наклона кривой.
Типичная кинетическая кривая:
При рассмотрении кинетики
химических реакций в закрытой системе обычно изучают на опыте
зависимость концентрации
какого-либо компонента от времени
и изображают эту зависимость
в виде графика, который называется
кинетической кривой.
Слайд 8;
Скорость реакции равна скорости уменьшения концентрации реагента А во
Соотношение между скоростью и концентрацией называют кинетическим уравнением:
-скорость реакции, кмоль/ м3
,
где k – константа скорости; n – порядок реакции.
Константа и скорость реакции не зависят от концентрации продуктов.
, моль/л.
Слайд 9 Порядок реакции
Если зависимость скорости
,
то величины ni (i=1, 2, …) принято называть порядком реакции относительно вещества Ai
Порядок реакции есть сумма показателей степени n1 + n2 + n3 + …, где порядок относительно реагента A1—n1,относительно A2—n2, относительно A3— n3 и т. д.
А В + С
Если для приведенной выше реакции экспериментально найдено, что скорость пропорциональна концентрации реагента А, реакция называется реакцией первого порядка, так как
Если скорость пропорциональна квадрату концентрации реагента А, реакция называется реакцией второго порядка, так как
Слайд 10 Константа скорости
Единицы измерения константы скорости зависят от порядка реакции. Так для реакций константа скорости измеряется в единицах :
первого порядка - [время]-1;
второго порядка - [концентрация]-1·[время]-1, например, дм3•моль-1•с-1.
нулевого порядка - моль•дм-3•с-1
третьего порядка — дм6•моль-2•с-1
В общем случае константа скорости реакции n-го порядка измеряется в единицах [концентрация]1-n·[время]-1..
Константы скорости реакций разных порядков являются разными физическими величинами и сопоставление их абсолютных значений не имеет смысла.
Слайд 11Кинетические уравнения первого порядка
Рассмотрим реакцию:
Пусть а — начальная концентрация реагента А; x —уменьшение ее за время t. Тогда концентрация А в момент t равна а —х. Выражение для скорости реакции примет вид
и кинетическое уравнение
можно записать как
дифференциальное
кинетическое уравнение
первого порядка
1
Интегрированием последнего уравнения получаем:
интегральное кинетическое
уравнение первого порядка
2
Слайд 12
Определение константы скорости реакции первого порядка
Выразим константу скорости
3
Или используя десятичный логарифм:
4
Слайд 13 Метод подстановки
Зная значения
Графический метод
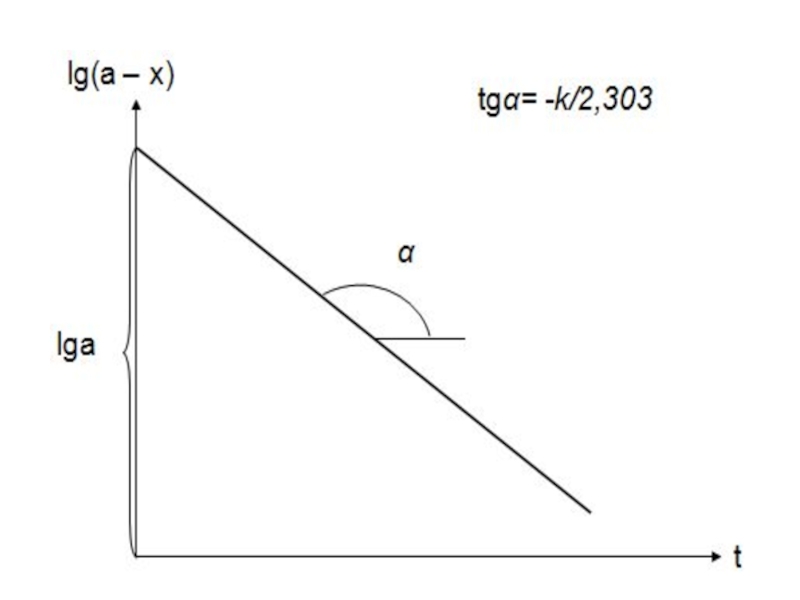
Из уравнения (4) видно, что для реакции первого порядка зависимость
от t должна представлять собой прямую с тангенсом угла наклона,
равным k/2,303. Уравнение (4) можно также преобразовать к виду
Зависимость lg(a – x) от t будет линейной с тангенсом угла наклона, равным -k/2,303.
Строится график в координатах [ lg(a – x), t ]. Константа скорости определяется из угла наклона полученной прямой. Графическое определение k дает лучшие результаты, чем метод подстановки.
Слайд 15Кинетические уравнения второго порядка
Рассмотрим реакцию:
Пусть начальные концентрации реагентов А и В равны cоответственно а и b, и х — уменьшение концентраций реагентов А и В за время t. Тогда в момент t концентрации A и В равны а —х и b —х. Кинетическое уравнение:
принимает вид
- дифференциальное
кинетическое уравнение
второго порядка
Интегрированием последнего уравнения получаем:
5
Слайд 16
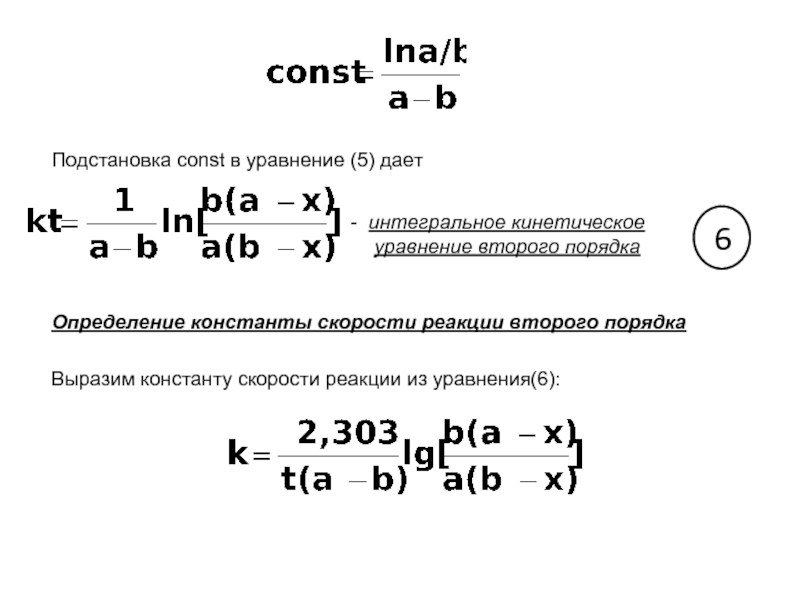
Подстановка const в уравнение (5) дает
интегральное
уравнение второго порядка
6
Определение константы скорости реакции второго порядка
Выразим константу скорости реакции из уравнения(6):
Слайд 17 Метод подстановки
Константу скорости
Графический метод
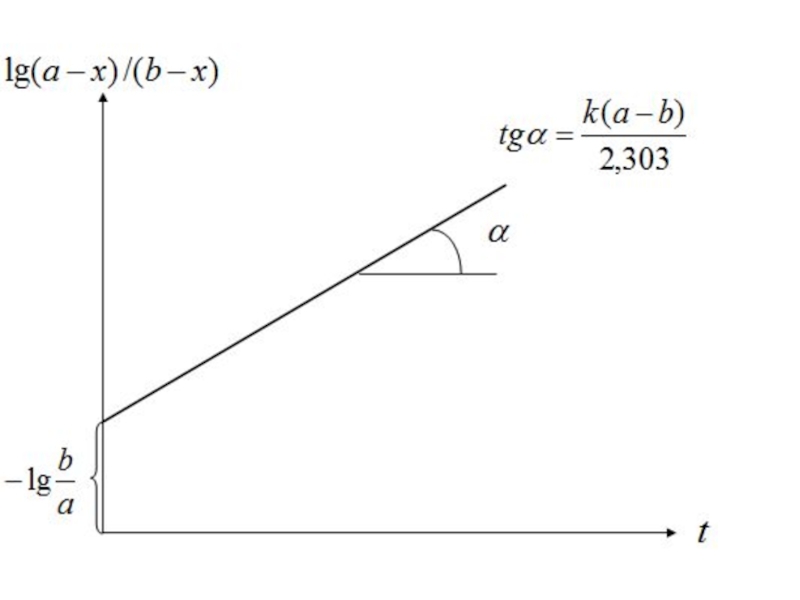
Для реакции второго порядка уравнение (6) можно преобразовать к виду
Зависимость \g(a — x)/(b — х) от t должна быть линейной с тангенсом угла наклона, равным k(a—b)/2,303, из которого можно найти k.
Слайд 19 Кинетические уравнения третьего порядка
Рассмотрим
А + В + С Продукты.
Если a, b и с — начальные концентрации реагентов А, В и С соответственно их — уменьшение этих концентраций за время t, то дифференциальное кинетическое уравнение третьего порядка имеет вид
В простейшем случае, когда все начальные концентрации одинаковы и равны а, предыдущее уравнение может иметь вид
7
После интегрирования уравнения (7) получим
8
Слайд 20
Подстановка const в уравнение (8) дает
интегральное кинетическое
уравнение третьего порядка
Константу скорости можно определить подстановкой соответствующих экспериментальных данных в уравнение (9), или из графической зависимости 1/(а—х)2 от t .
9
Слайд 21Кинетика сложных реакций
Большинство реакций являются сложными и состоят
Для описания кинетики сложных реакций используют принцип независимости, согласно которому при протекании в системе нескольких реакций каждая из них протекает независимо от других и подчиняется основному закону кинетики. Следует заметить, что этот принцип не является абсолютно строгим и не выполняется, например, для сопряженных реакций.
Двусторонние (обратимые) реакции
Рассмотрим обратимую реакцию первого порядка
k1
к-1
где k1 и k -1 — константы скорости соответственно прямой и обратной реакций.
А
В
Слайд 22 Пусть а — начальная концентрация реагента А,
Скорость реакции определяется уравнением
Где - равновесная концентрация вещества А.
,
10
Слайд 23 Интегрирование кинетического уравнения (10) при начальных условиях
Полученное соотношение можно записать в виде:
Таким образом, при обратимой реакции должна соблюдаться линейная
зависимость .
Определив из экспериментальных данных равновесные значения и
можно вычислить константу равновесия
По значениям величины и можно вычислить и :
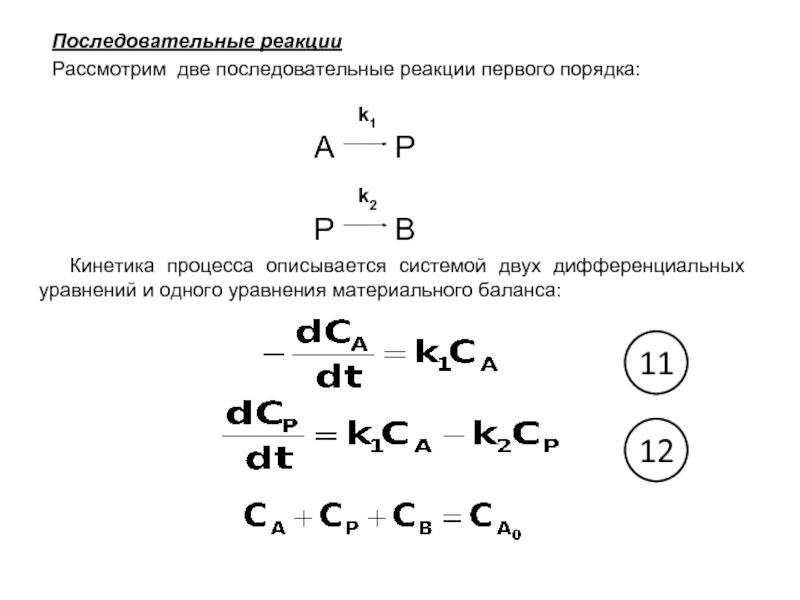
Слайд 24 Последовательные реакции
Рассмотрим две
k1 A Р
k2 Р В
Кинетика процесса описывается системой двух дифференциальных уравнений и одного уравнения материального баланса:
11
12
Слайд 25
Интегрированием уравнения
или
Таким образом, в координатах ln(СА,0/CA) – t определяют значение константы скорости k1 как тангенс угла наклона.
Подстановка выражения (13) в дифференциальное уравнение (12) приводит к уравнению :
13
Слайд 26При интегрировании полученного дифференциального уравнения при начальных условиях: СР=0, СА=СА,0 и
С помощью уравнения материального баланса и кинетических уравнений для А и Р (11 и 12) находят выражение для конечного продукта В:
Слайд 27 Параллельные реакции
Рассмотрим две
k1 A В1
k2 A В2
Дифференциальное уравнение для вещества А имеет вид:
Интегрирование этого уравнения СА=СА,0 и t=0 приводит к выражению:
Слайд 28 Дифференциальные уравнения для продуктов В1 и В2
Интегрирование этих уравнений соответственно при начальных условиях
СВ1=0, СВ2=0 и t=0 приводит к выражениям:
Слайд 29 Таким образом, для химического процесса, протекающего по
Сопряженные реакции
Реакции вида: А + В→ М (1) и А + D→ N (2)
Из которых одна реакция (2) протекает лишь совместно с другой, то есть индуцируется (1) реакцией. При этом вещество В называется индуктором, вещество А (участвующее в обеих реакциях) называется актором. Вещество D – акцептор. Связующим звеном в таких реакциях является промежуточный продукт, образованный в результате 1-ой реакции.
Шилов классифицировал реакции на 3 группы. В основе классификации он положил зависимость концентрации индукторов от времени.
1) реакции, когда концентрация индукторов во времени убывает. Это обычные сопряженные реакции.
2) реакции, когда концентрация индукторов во времени не меняется. Это каталитические реакции.
3) реакции, когда концентрация индукторов во времени возрастает. Это самоускоряющиеся автокаталитические реакции.
Слайд 30
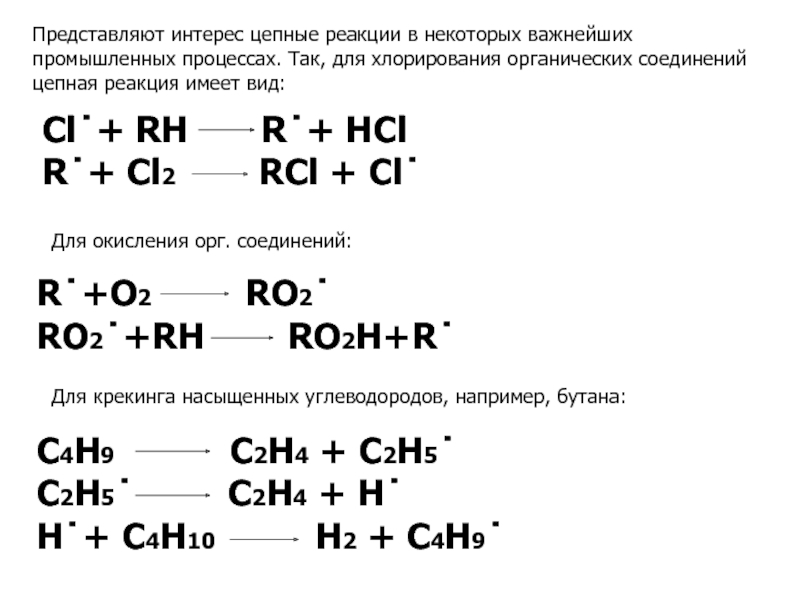
Слайд 31Представляют интерес цепные реакции в некоторых важнейших промышленных процессах. Так, для
Для окисления орг. соединений:
Для крекинга насыщенных углеводородов, например, бутана:
Cl˙+ RH R˙+ HCl
R˙+ Cl2 RCl + Cl˙
R˙+O2 RO2˙
RO2˙+RH RO2H+R˙
C4H9 C2H4 + C2H5˙
C2H5˙ C2H4 + H˙
H˙+ C4H10 H2 + C4H9˙
Слайд 32Метод стационарных концентраций
Для описания кинетики многостадийных реакций можно
Рассмотрим реакцию, которая протекает по схеме:
– интермедиат