- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Ких-фильтры с линейной фчх презентация
Содержание
- 1. Ких-фильтры с линейной фчх
- 2. КИХ фильтры с линейной ФЧХ В
- 3. Пример Найти фазочастотную характеристику КИХ-фильтра, описываемого передаточной
- 4. Пример Отсюда следует
- 5. АЧХ и ФЧХ рассмотренного КИХ-фильтра второго порядка
- 6. Теорема о КИХ-фильтрах
- 7. Теорема о КИХ-фильтрах
- 8. Следствие 1 Соотношение порождает два типа качественно различных ФЧХ:
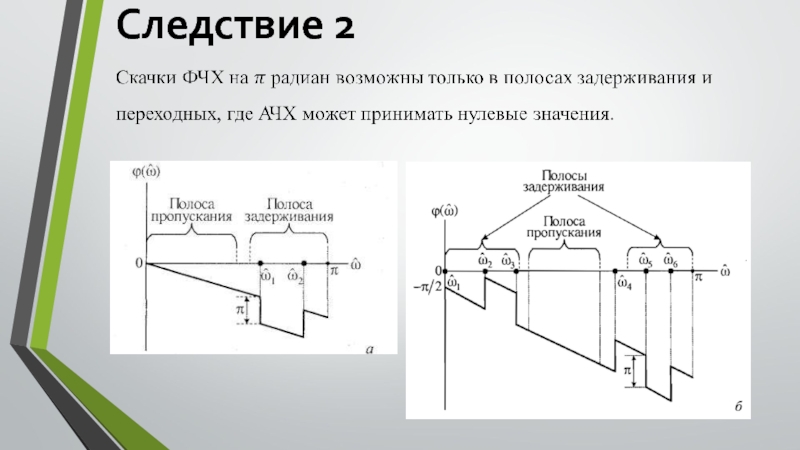
- 9. Следствие 2
- 10. Следствие 3 Групповое время задержки фильтра с
- 11. Следствие 4 или антисимметрична где N- длина импульсной характеристики КИХ фильтра.
- 12. Следствие 5 Типы КИХ-фильтров с линейной ФЧХ
- 13. Структурные схемы КИХ-фильтров с
- 14. Структурные схемы КИХ-фильтров с
- 15. Структурные схемы КИХ-фильтров с линейной ФЧХ
- 16. КИХ-фильтры типа 1.
- 17. КИХ-фильтры типа 1.
- 18. КИХ-фильтры типа 3.
- 19. КИХ-фильтры типа 3.
- 20. КИХ-фильтры типа 2.
- 21. КИХ-фильтры типа 2.
- 22. КИХ-фильтры типа 4.
- 23. КИХ-фильтры типа 4.
- 24. Параметры КИХ-фильтров
- 25. Параметры КИХ-фильтров
Слайд 2КИХ фильтры с линейной ФЧХ
В классе КИХ-фильтров можно синтезировать фильтры,
а потому и постоянным групповым временем задержки (ГВЗ):
т.е. начальные фазы всех частотных составляющих сигнала получают пропорциональный частоте сдвиг, поэтому не нарушаются их фазовые соотношения.
Слайд 3Пример
Найти фазочастотную характеристику КИХ-фильтра, описываемого передаточной функцией
Получим из передаточной функции
Отсюда вещественная и мнимая часть
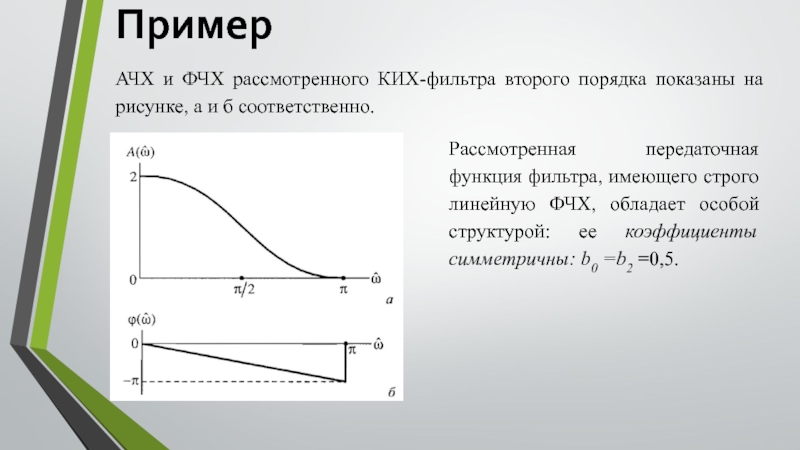
Слайд 5АЧХ и ФЧХ рассмотренного КИХ-фильтра второго порядка показаны на рисунке, а
Пример
Рассмотренная передаточная функция фильтра, имеющего строго линейную ФЧХ, обладает особой структурой: ее коэффициенты симметричны: b0 =b2 =0,5.
Слайд 6Теорема о КИХ-фильтрах
Пусть имеются два многочлена
где: di — вещественные коэффициенты;
D(z) — минимально-фазовый многочлен, т. е. его нули лежат в пределах единичного круга z-плоскости.
Тогда цифровой фильтр с передаточной функцией
Слайд 7Теорема о КИХ-фильтрах
При условии, что
имеет строго линейную ФЧХ вида
во всем диапазоне частот
с точностью до скачков фазы π на радиан на тех частотах ωk, где АЧХ принимает нулевое значение.
Слайд 10Следствие 3
Групповое время задержки фильтра с линейной ФЧХ постоянно и равно
причем
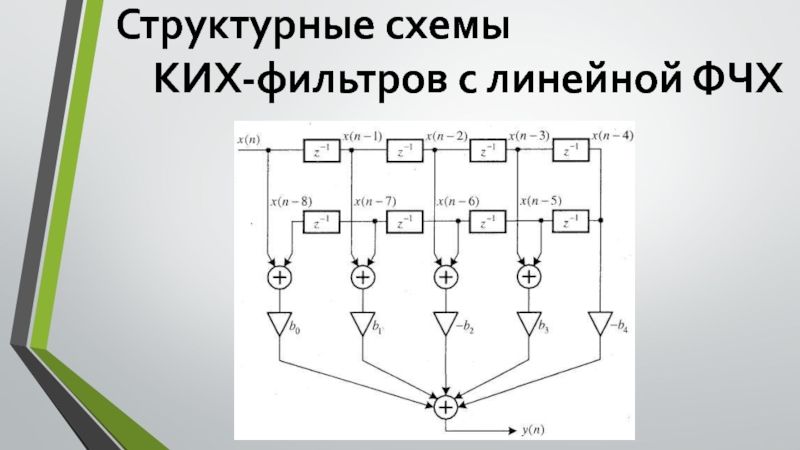
Слайд 13Структурные схемы
КИХ-фильтров с линейной ФЧХ
Построим структурную схему фильтра
Таким условиям соответствует фильтр типа 1, передаточная функция которого имеет вид
Слайд 14Структурные схемы
КИХ-фильтров с линейной ФЧХ
Объединим члены передаточной функции,
Полученную передаточную функцию и соответствующую ей схему будем называть приведенными.