- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Гидромеханика. Основные понятия и определения презентация
Содержание
- 1. Гидромеханика. Основные понятия и определения
- 2. Глава 1. ОСНОВНЫЕ ПОНЯТИЯ
- 3. Модель сплошной среды Жидкости и газы
- 4. Модель сплошной среды Эти допущения корректны:
- 5. Элементарный объём Элементарный объём - это
- 6. 1.2. Физические свойства жидкостей и газов
- 7. 1.2. Физические свойства жидкостей и газов
- 8. 33 1.2. Физические свойства жидкостей и газов
- 9. 1.2. Физические свойства жидкостей и газов
- 10. 33 1.2. Физические свойства жидкостей и газов
- 11. 1.2. Физические свойства жидкостей и газов
- 12. 1.2. Физические свойства жидкостей и газов
- 13. 1.2. Физические свойства жидкостей и газов
- 14. 1.2. Физические свойства жидкостей и газов
- 15. 1.2. Физические свойства жидкостей и газов
- 16. Условная вязкость жидкости Условная
- 17. Идеальная жидкость В
- 18. 1.3. Силы, действующие на жидкость Массовыми
- 19. Массовые силы Вектор
- 20. Поверхностные силы В случаях,
- 21. Поверхностные силы
- 22. Силы, действующие на жидкость
- 23. Силы, действующие на жидкость
- 24. Контрольные вопросы Что такое
- 25. Глава 2. ГИДРОСТАТИКА ФГБОУ ГУМРФ В
- 26. 2.1. Гидростатическое давление и его свойства
- 27. Свойства гидростатического давления: Величина гидростатического давления
- 28. 2.2. Дифференциальные уравнения равновесия жидкости (уравнения Эйлера
- 29. 2.2. Дифференциальные уравнения равновесия жидкости (уравнения Эйлера
- 30. Уравнения Эйлера выражают 1-й закон Ньютона применительно
- 31. Дифференциальные уравнения равновесия жидкости (уравнения Эйлера ).
- 32. 2.3. Основное уравнение гидростатики Рассмотрим частный случай
- 33. 2.3. Основное уравнение гидростатики Интегрируя третье уравнение
- 34. 2.3. Основное уравнение гидростатики Следствие Закон Паскаля:
- 35. 2.4. Способы измерения давления и вакуума
- 36. 2.4. Способы измерения давления и вакуума
- 37. 2.4. Способы измерения давления и вакуума
- 38. 2.4. Способы измерения давления и вакуума
- 39. 2.4. Способы измерения давления и вакуума
- 40. 2.4. Способы измерения давления и вакуума
- 41. 2.4. Способы измерения давления и вакуума
- 42. 2.5. Простейшие гидравлические машины Гидравлический пресс Если
- 43. 2.5. Простейшие гидравлические машины Мультипликатор В камере
- 44. 2.6. Сила давления на плоскую стенку К
- 45. 2.6. Сила давления на плоскую стенку статический
- 46. 2.6. Сила давления на плоскую стенку
- 47. 2.6. Сила давления на плоскую стенку Давление
- 48. 2.6. Сила давления на плоскую стенку Поскольку
- 49. 2.6. Сила давления на плоскую стенку Для
- 50. 2.6. Сила давления на плоскую стенку Уравнение
- 51. 2.6. Сила давления на плоскую стенку Получим:
- 52. 2.6. Сила давления на плоскую стенку Известно,
- 53. 2.6. Сила давления на плоскую стенку
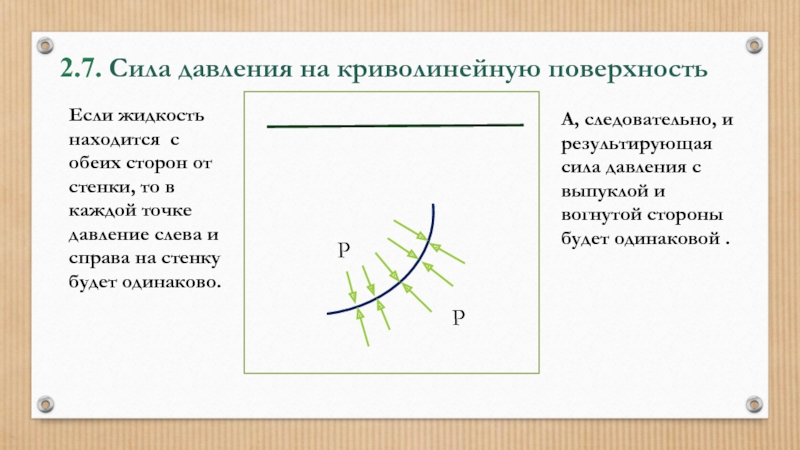
- 54. 2.7. Сила давления на криволинейную поверхность
- 55. 2.7. Сила давления на криволинейную поверхность
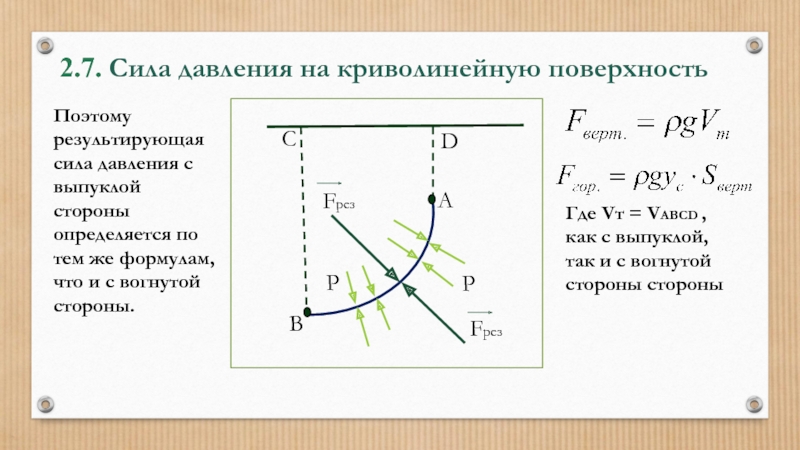
- 56. 2.7. Сила давления на криволинейную поверхность
- 57. 2.7. Сила давления на криволинейную поверхность
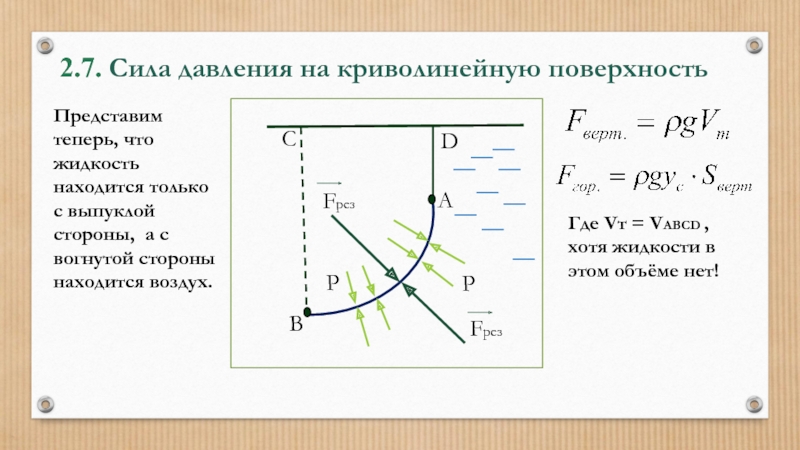
- 58. 2.7. Сила давления на криволинейную поверхность
- 59. 2.7. Сила давления на криволинейную поверхность
- 60. 2.7. Сила давления на криволинейную поверхность
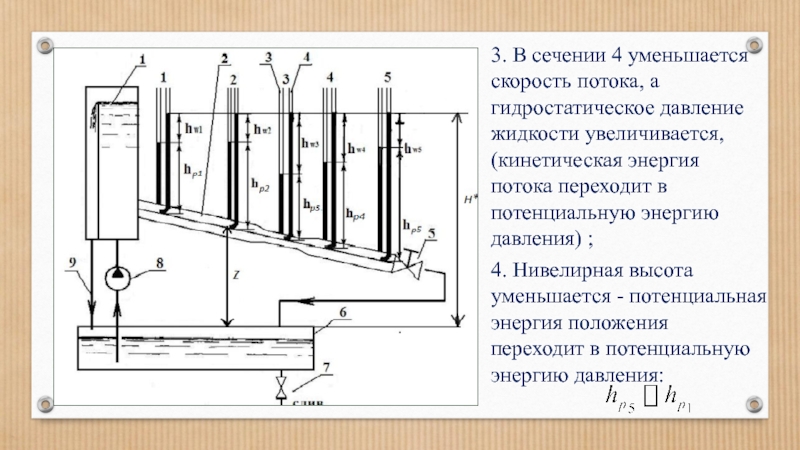
- 61. 2.7. Сила давления на криволинейную поверхность
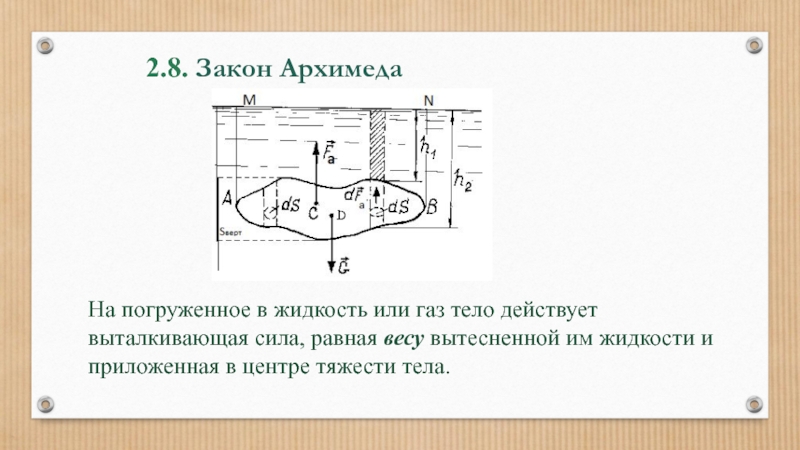
- 62. 2.8. Закон Архимеда На погруженное в жидкость
- 63. 2.8. Закон Архимеда На поверхность АКB действует
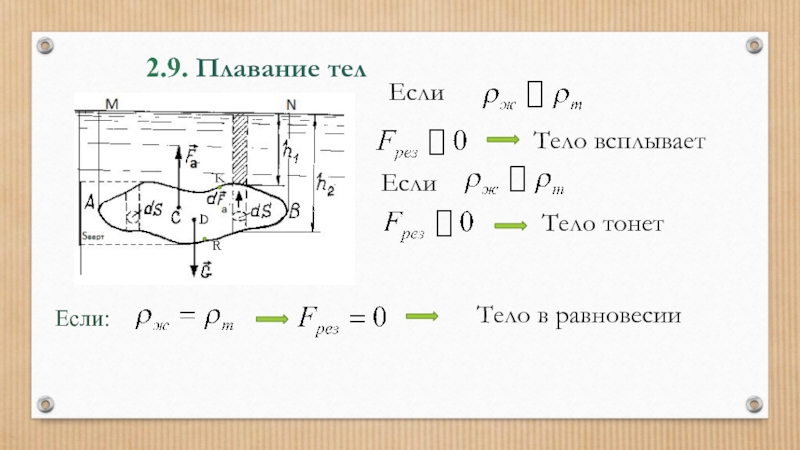
- 64. 2.9. Плавание тел Собственный вес твердого тела
- 65. 2.9. Плавание тел
- 66. Контрольные вопросы Что такое
- 67. Глава 3. ОСНОВЫ КИНЕМАТИКИ
- 68. Метод Лагранжа Для каждой мысленно выделенной i-й
- 69. Метод Эйлера Метод Эйлера, заключается в задании
- 70. Основное отличие в методах Лагранжа и Эйлера
- 71. Метод Эйлера Метод Эйлера, заключается в задании
- 72. Проекции ускорения на координатные оси:
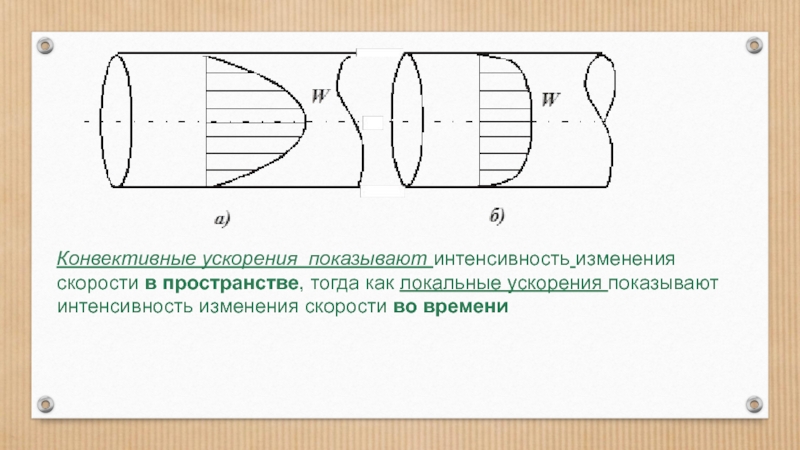
- 73. Члены показывают интенсивность
- 74. Конвективные ускорения показывают
- 75. 3.2. Поток жидкости и его характеристики
- 76. Линией тока называется такая линия в потоке
- 77. След движения частицы называется ее траекторией.
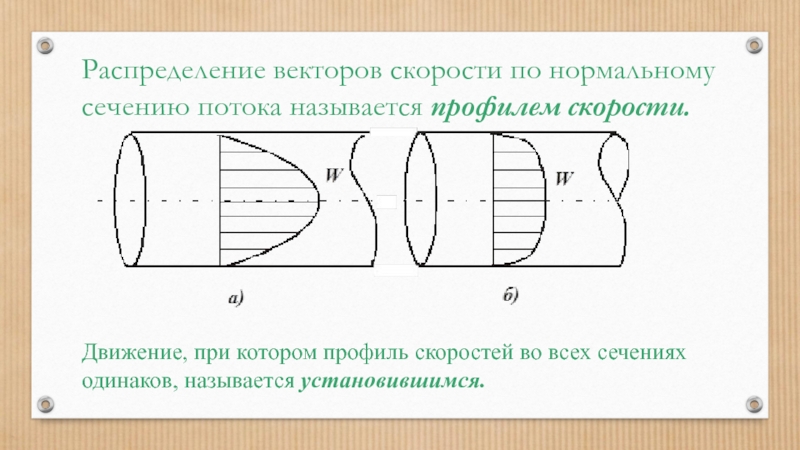
- 78. Распределение векторов скорости по нормальному сечению потока
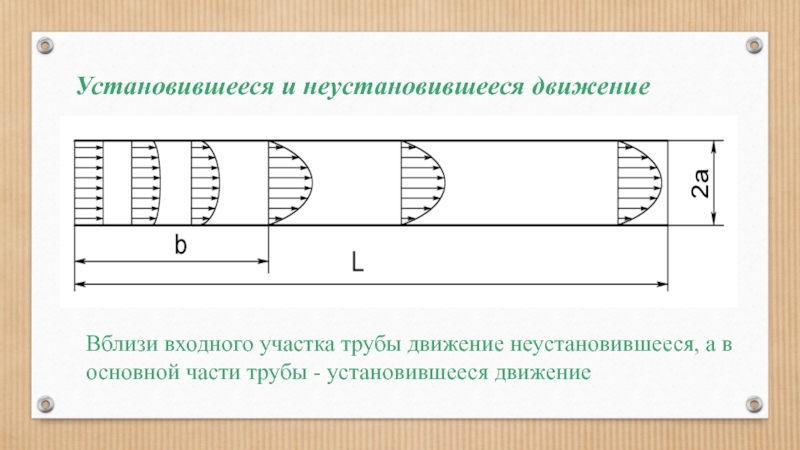
- 79. Установившееся и неустановившееся движение Вблизи входного участка
- 80. Установившееся и неустановившееся движение
- 81. Расход – это количество жидкости или газа,
- 82. Пространственным называется движение жидкости, параметры которого зависят
- 83. Движение, при котором отсутствует перемешивание между слоями
- 84. 3.3. Уравнение неразрывности движения жидкости Уравнение неразрывности
- 85. Для частных случаев движения жидкости уравнение неразрывности
- 86. Для стационарного потока жидкости в непроницаемом
- 87. Следовательно, массовый расход жидкости G через любое
- 88. Контрольные вопросы Какое движение
- 89. 4. ДИНАМИКА ИДЕАЛЬНОЙ
- 90. Дифференциальные уравнения движения идеальной жидкости (уравнения
- 91. Уравнения Эйлера выражают 2-й закон Ньютона применительно
- 94. Для того, чтобы система
- 95. Условие скольжения на твёрдой стенке касательная
- 96. 4.2. Уравнение Бернулли для идеальной жидкости Пусть
- 97. Это означает, что: Подставим эти выражения в
- 98. Получим: ; заметим, что:
- 99. Обозначим - трёхчлен Бернулли
- 100. Рассмотрим частный случай, когда идеальная жидкость движется
- 101. Закон Бернулли является частным случаем закона сохранения
- 102. Уравнение Бернулли для потока идеальной жидкости Для
- 103. Уравнение Бернулли для потока идеальной жидкости Умножим
- 104. Здесь скоростной напор, Па; гидростатическое
- 105. Уравнение Бернулли для потока идеальной жидкости Разделим
- 106. Здесь Скоростная высота, м; Пьезометрическая
- 107. Скоростная высота, м; Пьезометрическая высота,
- 108. Скоростную высоту можно определить
- 109. Полный напор Н* сохраняет своё значение; В
- 110. 3. В сечении 4 уменьшается скорость потока,
Слайд 1ГИДРОМЕХАНИКА
Является предшествующей дисциплинам:
«Судовые вспомогательные механизмы, системы и устройства», «Судовые котельные
«Судовые холодильные установки и системы кондиционирования воздуха», «Судовые двигатели внутреннего сгорания»,
«Судовые турбомашины».
Слайд 2
Глава 1.
ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
ФГБОУ ГУМРФ
1.1. Предмет гидромеханики.
Гидромеханика изучает законы равновесия и движения жидкостей и газов, их взаимодействие с омываемыми ими поверхностями твердых тел.
Гидромеханика разделяется на статику (гидростатику), кинематику и динамику.
Слайд 3
Модель сплошной среды
Жидкости и газы рассматриваются как сплошная среда, которой приписываются
Основные положения модели:
Любой малый макроскопический объём имеет такие же свойства, что и объём сравнительно больших размеров
Все физические свойства жидкостей и газов считаются непрерывными функциями координат и времени
Производные от этих функций также являются непрерывными функциями координат и времени.
Слайд 4
Модель сплошной среды
Эти допущения корректны:
если размеры рассматриваемой области жидкости или
если количество молекул в рассматриваемом объёме достаточно, чтобы физические свойства можно было считать непрерывными (газ не разреженный).
Слайд 5
Элементарный объём
Элементарный объём - это объём, размеры которого много больше размеров
Слайд 6
1.2. Физические свойства жидкостей и газов
Сплошность – жидкости и газы движутся
Текучесть - способность совершать непрерывное, неограниченное движение в пространстве и времени под действием приложенных сил или по инерции.
Следствия:
Жидкости и газы не имеют собственной формы и принимают форму сосуда, в который они помещены.
Газ занимает весь предоставленный ему объём.
Слайд 7
1.2. Физические свойства жидкостей и газов
Плотность – масса единицы объёма вещества,
Удельный объём – объём, занимаемый 1 кг вещества, (υ , м3/кг).
Под плотностью жидкости в данной точке понимается :
Слайд 833
1.2. Физические свойства жидкостей и газов
тепловое расширение – способность жидкостей и
Характеризуется коэффициентом теплового расширения βt, К-1 :
(1)
Он равен относительному изменению плотности (объёма) при изменении температуры на один Кельвин (К) при постоянном давлении
Слайд 9
1.2. Физические свойства жидкостей и газов (тепловое расширение )
Проинтегрируем выражение (1)
Если плотность меняется незначительно, можно использовать упрощённые формулы:
Слайд 1033
1.2. Физические свойства жидкостей и газов
Объёмное сжатие– способность жидкостей и газов
Характеризуется коэффициентом объёмного сжатия βр, Па-1 :
(2)
Он равен относительному изменению плотности (объёма) при изменении давления на один Паскаль при постоянной температуре.
Слайд 11
1.2. Физические свойства жидкостей и газов (Объёмное сжатие)
Проинтегрируем выражение (2) :
Если плотность меняется незначительно, можно использовать упрощённые формулы:
Слайд 12
1.2. Физические свойства жидкостей и газов
Сжимаемость
Обратная коэффициенту βр величина называется модулем
Для воды при атмосферном давлении модуль Е составляет приблизительно 2000 МПа. Такого же порядка он и для других капельных жидкостей, например, для минеральных масел он равен приблизительно 1200 МПа.
Поэтому для многих задач сжимаемостью жидкостей можно пренебречь.
Слайд 13
1.2. Физические свойства жидкостей и газов
Вязкость – способность жидкостей и газов
При прямолинейном слоистом движении жидкости сила внутреннего трения F между смещающимися слоями выражается формулой Ньютона:
где μ - динамический коэффициент вязкости, кг/(м⋅c)= Па∙ с,
- величина градиента скорости.
Слайд 14
1.2. Физические свойства жидкостей и газов (вязкость)
Сила внутреннего трения F между
Касательные напряжения:
Слайд 15
1.2. Физические свойства жидкостей и газов (вязкость)
- динамический коэффициент вязкости,
Слайд 16
Условная вязкость жидкости
Условная вязкость жидкости (ВУ) измеряется в градусах Энглера, °
, м2/с
У жидкостей вязкость понижается при нагреве, а у газов - повышается.
Слайд 17
Идеальная жидкость
В гидромеханике идеальной называется невязкая и несжимаемая жидкость (ρ=const).
Идеальных жидкостей
Слайд 18
1.3. Силы, действующие на жидкость
Массовыми называются силы, приложенные ко всем точкам
К ним относятся, например, сила тяжести и силы инерции.
Массовые силы характеризуются
вектором плотности
распределения массовых сил:
Слайд 19
Массовые силы
Вектор плотности распределения массовых сил – это сила, действующая
Например, если на рассматриваемый объём действует сила тяжести:
Если известна величина вектора плотности распределения массовых сил, то легко определить массовую силу, действующую на выделенный объем:
F = ∫(f∙ρ∙dV)
Слайд 20
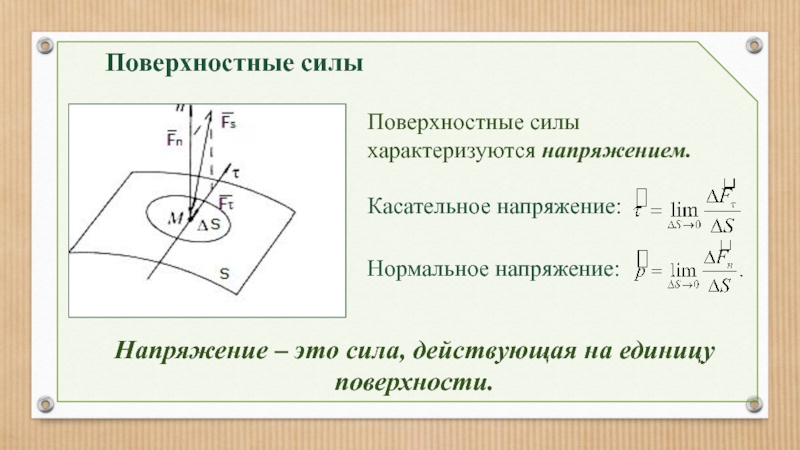
Поверхностные силы
В случаях, когда частицы жидкости, на которые действуют силы, расположены
Слайд 21
Поверхностные силы
Поверхностные силы характеризуются напряжением.
Касательное напряжение:
Нормальное напряжение:
Напряжение – это сила,
Слайд 22
Силы, действующие на жидкость
Основное различие между вектором плотности распределения массовых
Слайд 23
Силы, действующие на жидкость
Нормальные (по отношению к площадке ∆S) и
где и - орты нормали и касательной к площадке ∆S соответственно.
Скалярные величины р и τ не зависят от положения площадки ∆S и образуют скалярные поля.
Слайд 24
Контрольные вопросы
Что такое средняя плотность?
Что такое вязкость?
Какими коэффициентами оценивается вязкость и
Какая жидкость называется идеальной?
Какие виды сил действуют в жидкости?
Что такое вектор плотности распределения массовых сил?
Что такое напряжение?
Слайд 25Глава 2.
ГИДРОСТАТИКА
ФГБОУ ГУМРФ
В покоящейся жидкости не происходит относительного перемещения слоев,
Гидростатика изучает равновесие жидкостей и газов, находящихся в состоянии покоя.
Состояние покоя – это такое состояние, когда частицы среды не перемещаются относительно друг друга.
Слайд 26
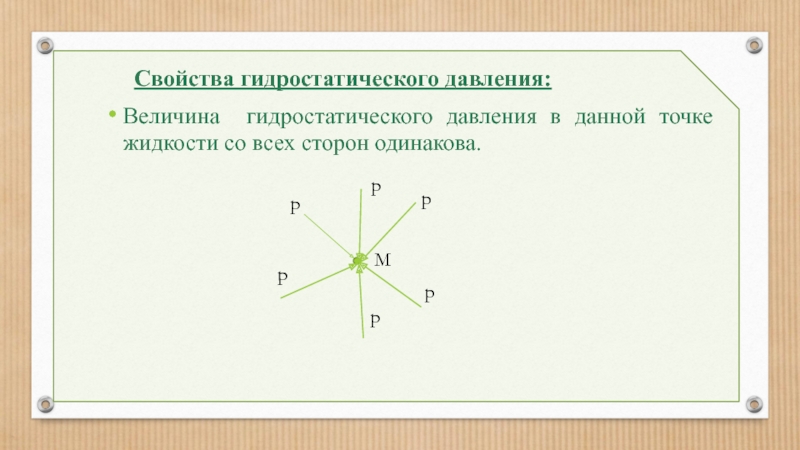
2.1. Гидростатическое давление и его свойства
Нормальные напряжения в покоящейся жидкости называются
Свойства гидростатического давления:
Давление всегда направлено по нормали к площадке, на которую оно действует;
Давление всегда стремится сжать выделенный объём;
Величина гидростатического давления в данной точке жидкости со всех сторон одинакова.
Слайд 27
Свойства гидростатического давления:
Величина гидростатического давления в данной точке жидкости со всех
М
р
р
р
р
р
р
Слайд 282.2. Дифференциальные уравнения равновесия жидкости (уравнения Эйлера ).
p=p(x,y,z)
Fx
Fy
Пусть, давление в центре
Тогда, давление на левой грани будет:
Давление на правой грани будет:
Слайд 292.2. Дифференциальные уравнения равновесия жидкости (уравнения Эйлера ).
Fx = fxρ∙dxdydz
Fx
Fy
Силы давления
Проекция массовой силы на ось х:
где fx - вектор плотности распределения массовых сил
Слайд 30Уравнения Эйлера выражают 1-й закон Ньютона применительно к жидкостям и газам
Условие равновесия выделенного объема жидкости в проекции на ось x :
Аналогично:
Слайд 322.3. Основное уравнение гидростатики
Рассмотрим частный случай равновесия жидкости, когда из массовых
В этом случае уравнения Эйлера упрощаются:
p=const(x)
p=const(y)
В покоящейся жидкости давление меняется только по вертикали, т.е. в любом горизонтальном слое жидкости давление во всех точках одинаково
Слайд 332.3. Основное уравнение гидростатики
Интегрируя третье уравнение системы, получим:
р - ρgz =
Граничные условия:
при z=0 p=p0 С=р0.
А
О
или
Слайд 342.3. Основное уравнение гидростатики
Следствие
Закон Паскаля: давление, приложенное к свободной поверхности жидкости
А
О
р- ро= ри =ρgh называется манометрическим или, избыточным давлением
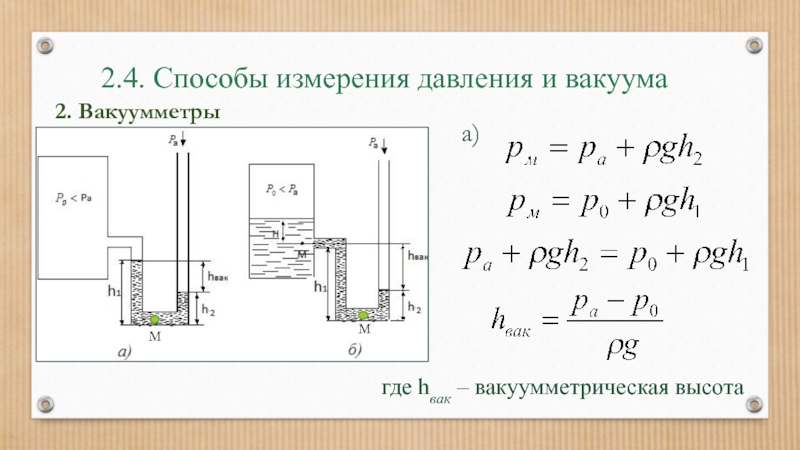
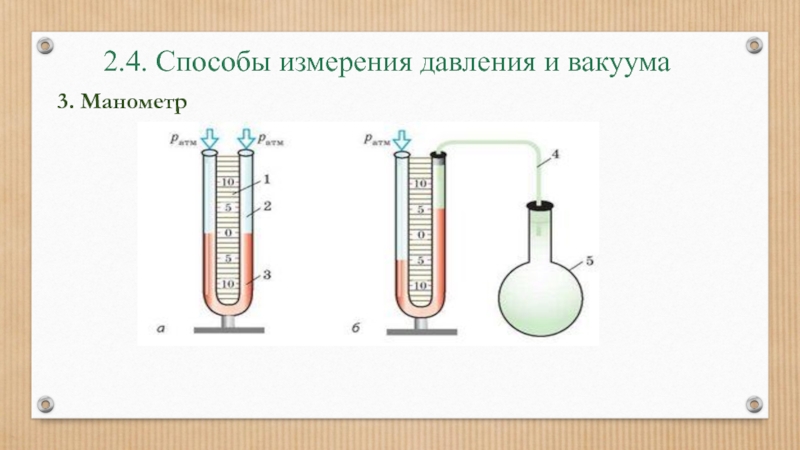
Слайд 352.4. Способы измерения давления и вакуума
где ри - избыточное давление на
1. Пьезометр
Слайд 362.4. Способы измерения давления и вакуума
Избыточному давлению в 1бар=105 Па соответствует
1. Пьезометр
м водяного столба;
мм ртутного столба;
γ=ρg – удельный вес жидкости.
- пьезометрическая высота
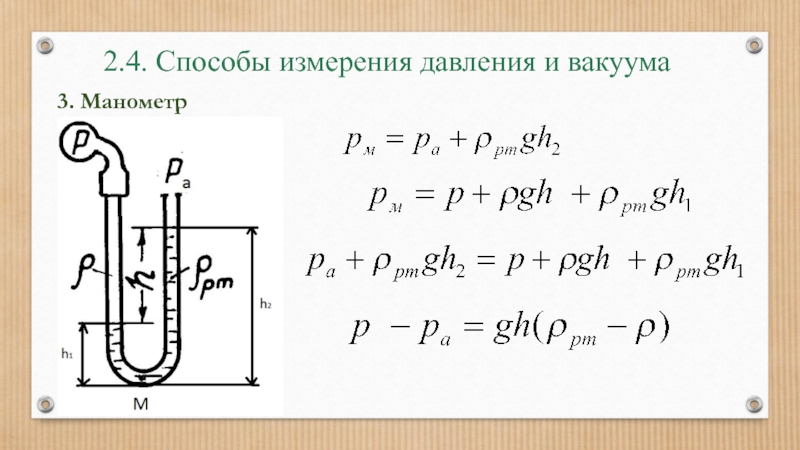
Слайд 372.4. Способы измерения давления и вакуума
где hвак – вакуумметрическая высота
2. Вакуумметры
а)
М
М
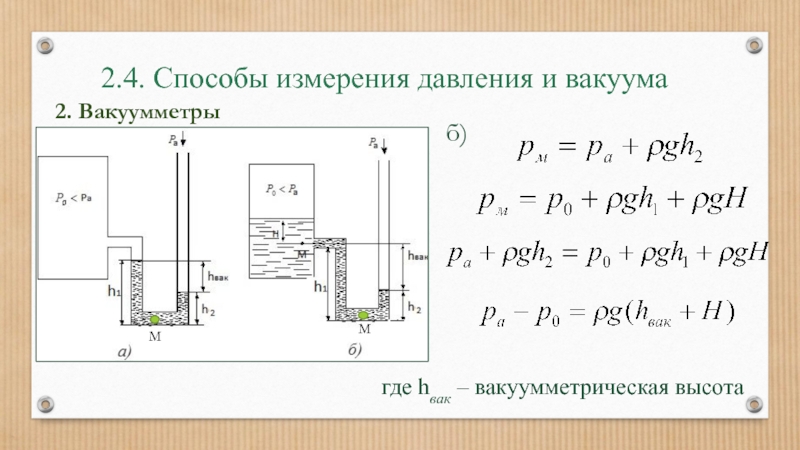
Слайд 382.4. Способы измерения давления и вакуума
где hвак – вакуумметрическая высота
2. Вакуумметры
б)
М
М
Слайд 422.5. Простейшие гидравлические машины
Гидравлический пресс
Если к поршню 1 с площадью S1
Гидростатическое
давление на поверхностях поршней одинаково:
Тогда сила F2 будет больше силы F1 в раз
Слайд 432.5. Простейшие гидравлические машины
Мультипликатор
В камере 1 к поршню площадью S1 приложена
Так как поршень камеры 2 площадью S2 воспринимает такую же силу, то он будет создавать гидростатическое давление р2 большее, чем р1 :
Тогда давление р2 будет больше давления р1 в раз.
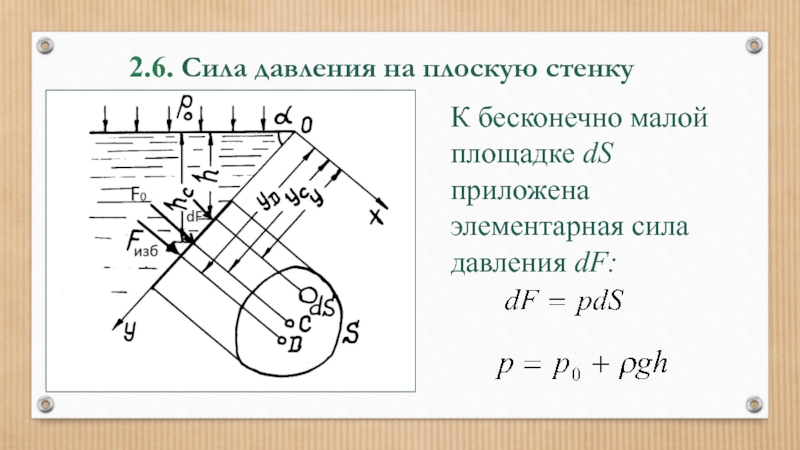
Слайд 442.6. Сила давления на плоскую стенку
К бесконечно малой площадке dS приложена
Слайд 452.6. Сила давления на плоскую стенку
статический момент площади S относительно оси
Известно, что:
Тогда:
Слайд 462.6. Сила давления на плоскую стенку
где F0 - сила внешнего давления
- сила избыточного давления
Где - глубина погружения центра тяжести площади S, - координата центра тяжести площади S
Слайд 472.6. Сила давления на плоскую стенку
Давление это распределённая нагрузка, которая мысленно
Слайд 482.6. Сила давления на плоскую стенку
Поскольку суммарная сила F складывается из
Внешнее давление р0 передается всем точкам площади одинаково, поэтому его равнодействующая сила F0 будет приложена в центре тяжести площади S (точка С).
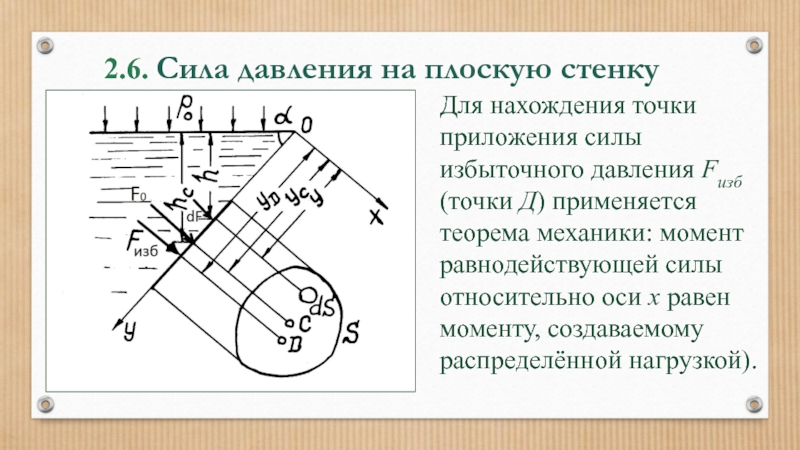
Слайд 492.6. Сила давления на плоскую стенку
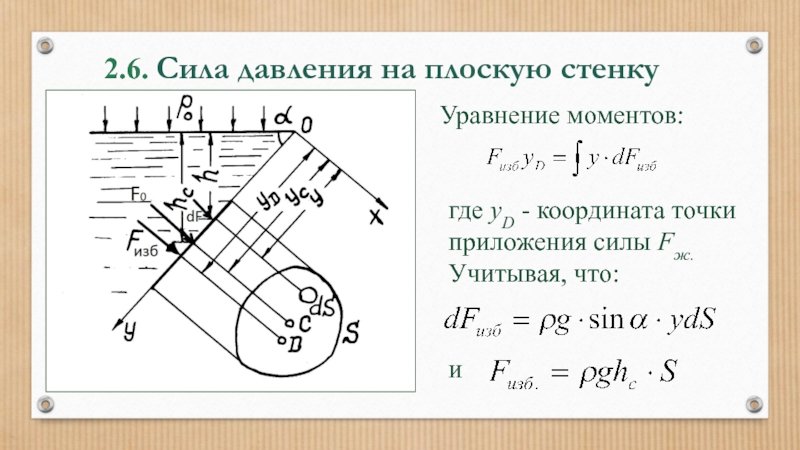
Для нахождения точки приложения силы избыточного
Слайд 502.6. Сила давления на плоскую стенку
Уравнение моментов:
где yD - координата
Учитывая, что:
и
Слайд 512.6. Сила давления на плоскую стенку
Получим:
- момент инерции площади S
Слайд 522.6. Сила давления на плоскую стенку
Известно, что:
Jxc - момент инерции
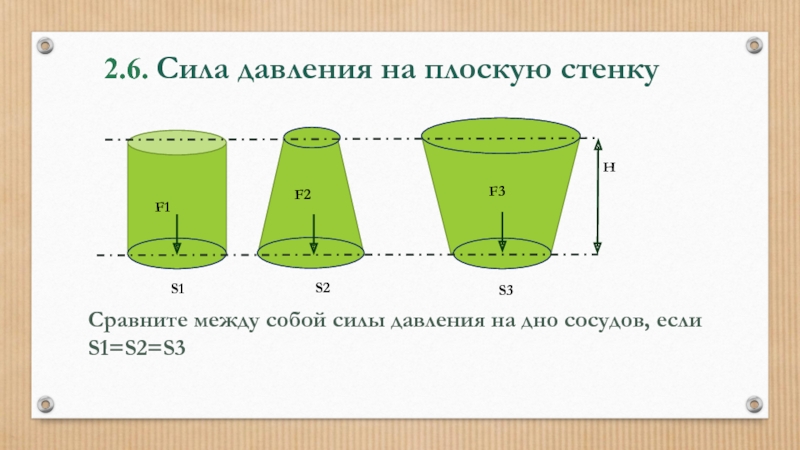
Слайд 532.6. Сила давления на плоскую стенку
Н
S1
S2
S3
F1
F2
F3
Сравните между собой силы давления на
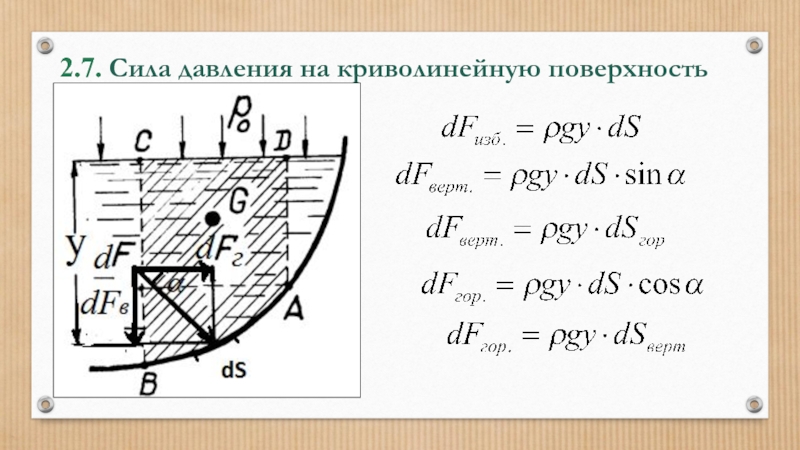
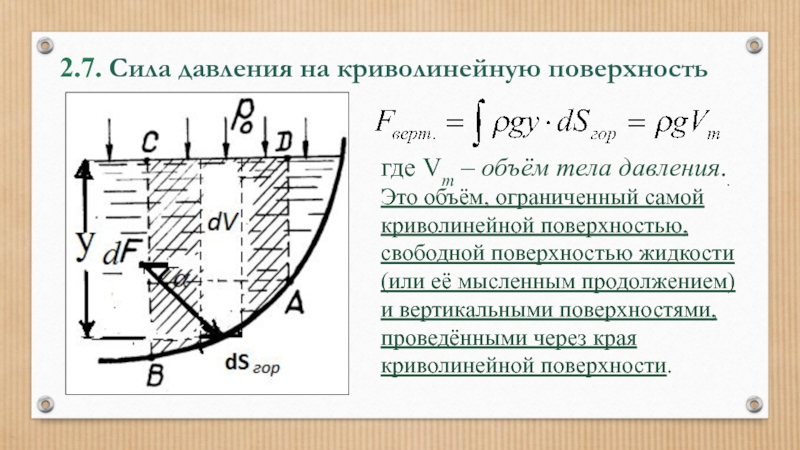
Слайд 552.7. Сила давления на криволинейную поверхность
где Vт – объём тела
Это объём, ограниченный самой криволинейной поверхностью, свободной поверхностью жидкости (или её мысленным продолжением) и вертикальными поверхностями, проведёнными через края криволинейной поверхности.
Слайд 562.7. Сила давления на криволинейную поверхность
где Sверт – вертикальная проекция
yc.- глубина погружения центра тяжести вертикальной проекции.
Слайд 572.7. Сила давления на криволинейную поверхность
где – угол наклона
Слайд 582.7. Сила давления на криволинейную поверхность
P
P
Если жидкость находится с обеих
А, следовательно, и результирующая сила давления с выпуклой и вогнутой стороны будет одинаковой .
Слайд 592.7. Сила давления на криволинейную поверхность
P
А
Поэтому результирующая сила давления с
Fрез
Fрез
P
В
С
D
Где Vт = VABCD , как с выпуклой, так и с вогнутой стороны стороны
Слайд 602.7. Сила давления на криволинейную поверхность
P
А
Представим теперь, что жидкость находится
Fрез
Fрез
P
В
С
D
Где Vт = VABCD , хотя жидкости в этом объёме нет!
Слайд 612.7. Сила давления на криволинейную поверхность
где – угол наклона
Слайд 622.8. Закон Архимеда
На погруженное в жидкость или газ тело действует выталкивающая
Слайд 632.8. Закон Архимеда
На поверхность АКB действует сила:
т.к. Sверт одинаковы
K
R
На поверхность
Результирующая сила, действующая на тело со стороны жидкости или газа:
Слайд 642.9. Плавание тел
Собственный вес твердого тела G приложен в центре тяжести
Сила Архимеда приложена в геометрическом центре тяжести тела
K
R
Результирующая сила, действующая на тело:
Слайд 66
Контрольные вопросы
Что такое гидростатическое давление?
Какими свойствами обладает гидростатическое давление?
Основное уравнение гидростатики
Закон
Как определить силу гидростатического давление на плоскую стенку?
Как определить силу гидростатического давления на криволинейную поверхность?
Сформулируйте закон Архимеда.
Слайд 67
Глава 3.
ОСНОВЫ КИНЕМАТИКИ ЖИДКОСТИ
Кинематика описывает движение жидкости без связи с
ФГБОУ ГУМРФ
3.1. Способы задания движения жидкости
Существует два основных способа задания движения жидкости:
метод Лагранжа и метод Эйлера
Слайд 68Метод Лагранжа
Для каждой мысленно выделенной i-й частицы жидкости определяется траектория её
Слайд 69Метод Эйлера
Метод Эйлера, заключается в задании поля скоростей:
(т.е. в задании зависимостей
Слайд 70Основное отличие в методах Лагранжа и Эйлера заключается в том, что
Слайд 73Члены
показывают интенсивность изменения скорости во времени
для частицы,
проходящей
это локальные или местные ускорения .
Остальные три члена в каждом уравнении показывают интенсивность
изменения скорости в пространстве, т.е. определяют ускорение частицы в связи с её переходом в соседнюю точку с другим значением скорости - это конвективные ускорения частиц.
Слайд 74
Конвективные ускорения показывают интенсивность изменения скорости в пространстве, тогда как
Слайд 753.2. Поток жидкости и его характеристики
Если параметры движения не зависят от
Если параметры движения зависят от времени, то такое движение называется нестационарным.
Слайд 76Линией тока называется такая линия в потоке жидкости, в каждой точке
Слайд 77След движения частицы называется ее траекторией. В случае стационарного поля скоростей
- средняя по времени скорость в данной точке
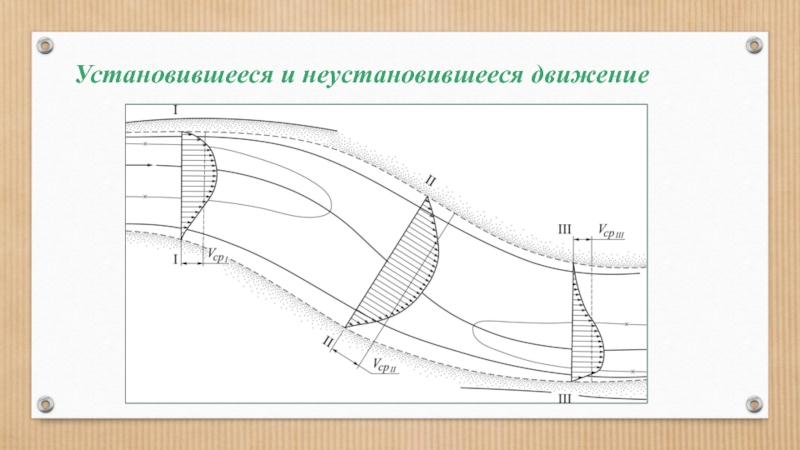
Слайд 78Распределение векторов скорости по нормальному сечению потока называется профилем скорости.
Движение, при
Слайд 79Установившееся и неустановившееся движение
Вблизи входного участка трубы движение неустановившееся, а в
Слайд 81Расход – это количество жидкости или газа, протекающее в единицу времени
Различают объёмный Q, м3/с и массовый G, кг/с расход жидкости:
- средняя по сечению скорость потока
Слайд 82Пространственным называется движение жидкости, параметры которого зависят от трех координат. Плоским называется
Слайд 83Движение, при котором отсутствует перемешивание между слоями жидкости, линии тока плавные
Слайд 843.3. Уравнение неразрывности движения жидкости
Уравнение неразрывности выражает закон сохранения массы применительно
Слайд 85Для частных случаев движения жидкости уравнение неразрывности будет упрощаться.
для стационарного движения
для плоского стационарного движения несжимаемой жидкости:
Для линейного стационарного движения сжимаемой жидкости:
Слайд 86
Для стационарного потока жидкости в непроницаемом канале (все частицы жидкости движутся
Слайд 87Следовательно, массовый расход жидкости G через любое нормальное сечение потока S
Для несжимаемой жидкости объёмный расход через любое нормальное сечение потока - также величина постоянная:
Q=wсрS=const
Откуда, для любых двух сечений потока: w1S1= w2S2
Следовательно, w2= w1S1/ S2.
Слайд 88
Контрольные вопросы
Какое движение называется стационарным?
Какое движение называется нестационарным?
Какое движение называется установившимся?
Что
Что такое профиль скорости?
Какое движение называется плоским?
Что такое расход?
Что такое местная скорость?
Напишите уравнение сплошности в гидравлической форме
Слайд 89
4. ДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ
Идеальной называется невязкая и несжимаемая жидкость.
ФГБОУ
4.1. Уравнения движения идеальной жидкости (уравнения Эйлера)
Уравнения движения Эйлера выражают 2-й закон Ньютона применительно к потоку идеальной жидкости.
Слайд 90 Дифференциальные уравнения движения идеальной жидкости (уравнения Эйлера ).
Fx = fxρ∙dxdydz
Fx
Fy
Силы
Проекция массовой силы на ось х:
где fx - вектор плотности распределения массовых сил
Слайд 91Уравнения Эйлера выражают 2-й закон Ньютона применительно к жидкостям и газам
Уравнение движения выделенного объема жидкости в проекции на ось x :
Аналогично:
Слайд 93
Уравнение неразрывности идеальной жидкости нужно присоединить к системе, чтобы она была
Слайд 94Для того, чтобы система была замкнутой, к
Граничные условия при обтекании невязкой жидкостью твердых поверхностей :
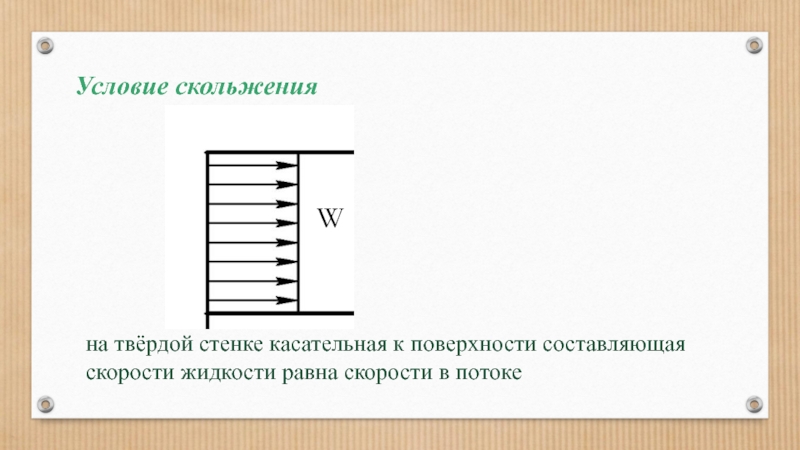
условие скольжения - на твёрдой стенке касательная к поверхности составляющая скорости жидкости равна скорости в потоке (т.е. стенка не оказывает тормозящего влияния на идеальную жидкость)
условие непротекания - равенство нулю на стенке нормальной составляющей скорости.
Слайд 95Условие скольжения
на твёрдой стенке касательная к поверхности составляющая скорости жидкости
W
Слайд 964.2. Уравнение Бернулли для идеальной жидкости
Пусть идеальная жидкость движется в потенциальном
Это означает, что существует такая функция П , что:
- вектор плотности распределения массовых сил
Слайд 99Обозначим
- трёхчлен Бернулли
Тогда:
Следовательно:
Следовательно, вдоль линии тока трехчлен Бернулли сохраняет постоянное значение.
Это
Слайд 100Рассмотрим частный случай, когда идеальная жидкость движется в поле сил тяжести,
С другой стороны: , откуда:
где С – константа интегрирования.
Подставим П в уравнение Бернулли:
- закон Бернулли для тяжёлой несжимаемой жидкости.
Слайд 101Закон Бернулли является частным случаем закона сохранения энергии применительно к потоку
удельная (Дж/кг) кинетическая энергия потока;
удельная (Дж/кг) потенциальная энергия сил давления;
удельная (Дж/кг) потенциальная энергия положения жидкости в поле сил тяжести
полная удельная энергия потока (Дж/кг) - величина постоянная
В
gz
Слайд 102Уравнение Бернулли для потока идеальной жидкости
Для двух произвольных сечений потока идеальной
Слайд 103Уравнение Бернулли для потока идеальной жидкости
Умножим левую и правую часть уравнения
, Па
Слайд 104Здесь
скоростной напор, Па;
гидростатическое давление, Па;
давление столба жидкости высотой z, Па;
полный
Р*
ρgz
Слайд 105Уравнение Бернулли для потока идеальной жидкости
Разделим левую и правую часть уравнения
, м
Слайд 106Здесь
Скоростная высота, м;
Пьезометрическая высота, м
Нивелирная высота, м (это расстояние от произвольной
гидравлическая высота (полный напор в метрах).
Н*
z
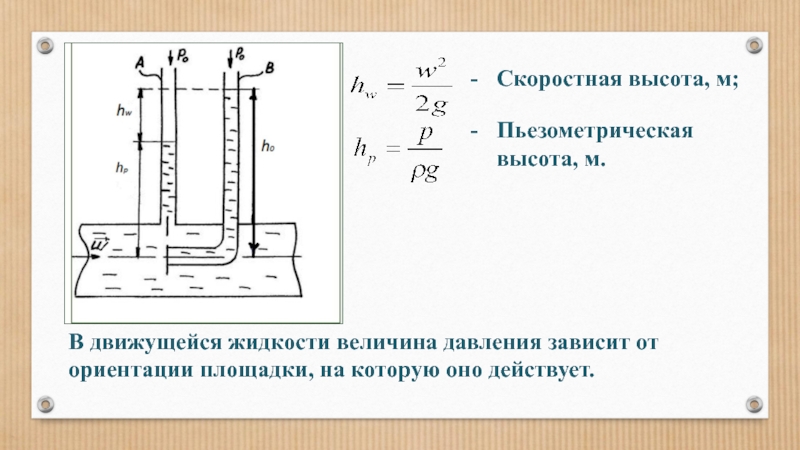
Слайд 107
Скоростная высота, м;
Пьезометрическая высота, м.
В движущейся жидкости величина давления зависит от
Слайд 108
Скоростную высоту
можно определить по разнице показаний прямого пьезометра и изогнутого
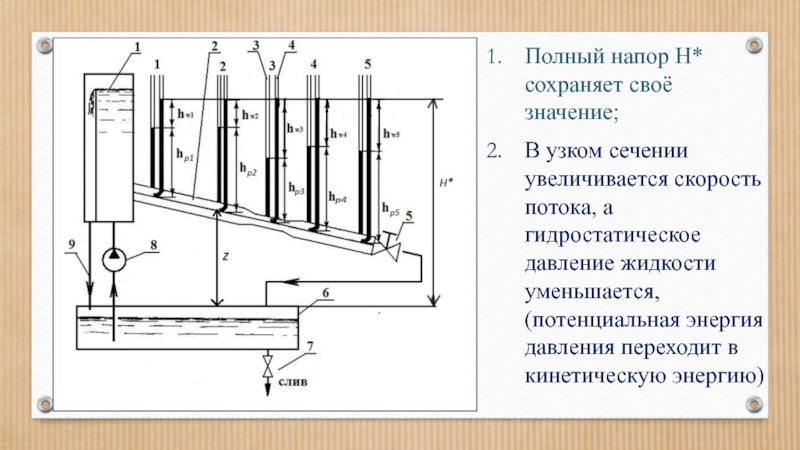
Слайд 109Полный напор Н* сохраняет своё значение;
В узком сечении увеличивается скорость потока,
Слайд 1103. В сечении 4 уменьшается скорость потока, а гидростатическое давление жидкости
4. Нивелирная высота уменьшается - потенциальная энергия положения переходит в потенциальную энергию давления: