- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Гравитационные волны (жидкость неограниченной глубины). Звуковые волны презентация
Содержание
- 1. Гравитационные волны (жидкость неограниченной глубины). Звуковые волны
- 2. Гравитационные волны (жидкость неограниченной глубины)
- 3. Гравитационные волны – волны на поверхности воды
- 4. Исходные допущения: Жидкость неограниченно большой глубины
- 5. Производимая волной разность давлений в
- 6. В итоге имеем решение вида:
- 7. Особенности гравитационных волн на глубокой воде 1.
- 8. Траектории частиц Компоненты вектора скорости В каждой
- 9. Уравнения движения частицы жидкости в параметрической форме.
- 10. Адиабатическая связь p(ρ) − следствие обычно быстрого
- 11. имеет место связь Линеаризация уравнений гидродинамики.
- 12. − волновое уравнение Так как v=∇ϕ
- 13. Плоские звуковые волны Опуская далее штрихи у
- 14. Продольность звуковых волн Обратимся к представлению волны
- 15. Шаровые и цилиндрические звуковые волны Решение
- 16. Волновое поле колеблющегося кварца размером в 4λ
Слайд 1Лекция 4
«Волны в идеальной жидкости»
Содержание:
Гравитационные волны (жидкость неограниченной глубины).
2. Звуковые
Слайд 2Гравитационные волны (жидкость
неограниченной глубины)
В современной физике волны – краеугольный камень
в
Оптика, акустика, электродинамика (радиофизика) – полностью волновые разделы физики.
Гидромеханика – волны (ударные и акустические) в атмосфере и гидросфере, волны на поверхностях и внутренних границах жидких сред (гравитационные волны, капиллярные волны, внутренние волны, волны в каналах и пр.).
Сфера приложений: метеорология, волнозащита прибрежных сооружений, кораблестроение (волнообразование при движении кораблей), защита от акустического шума, гидролокация.
Слайд 3Гравитационные волны – волны на поверхности воды (рис. 1), для
существования
Рис. 1
(отсюда название; не путать с
гравитационными волнами
специальной теории
относительности - предсказаны,
обнаружены 2016 г. )
Рис. 2
Возбуждаются: при ударе по
поверхности жидкости, ветровом
воздействии, движении кораблей.
Сила тяжести при вертикальных
отклонениях поверхности жидкости
– возвращающая сила.
Частицы жидкости во впадинах
выдавливаются вверх. Горбы и
впадины аналогичны сжатым и
растянутым пружинам осцилляторов.
Слайд 4Исходные допущения:
Жидкость неограниченно большой глубины −∞•z≤0
Отклонения поверхности ζ настолько малы, что
малые скорости v, позволяющие пренебречь нелинейным членом
в уравнении Эйлера и в силу условия |v|••c (с − скорость звука)
принять жидкость несжимаемой (ρ=const), а течение
потенциальным (v=∇ϕ).
Основная трудность решения заключается в формулировке граничного условия, поскольку поверхность жидкости не остается фиксированной и испытывает отклонения.
Обратимся с этой целью к уравнению,
которое должно выполняться во всей
области z≤ζ, включая и саму границу.
от координат
не зависит
Слайд 5
Производимая волной разность давлений
в точках границы z=ζ должна отсутствовать независимо
возмущений (граница с вакуумом). Отсюда имеем граничное условие
Решение уравнения Лапласа ищем в виде
Подстановка ⇒ к ОДУ
что дает
В области решения из-за возмущения границы волной z−ζ•0 и по
требованию ограниченности выбираем положительный знак
Слайд 6В итоге имеем решение вида:
Вывод дисперсионного соотношения
По условиям возбуждения величины
число k еще подлежит определению.
Преобразованное
граничное условие
Подстановка ϕ в ГУ:
приводит к дисперсионному соотношению
Дисперсионное соотношение дает
недостающее значение k и завершает построение решения
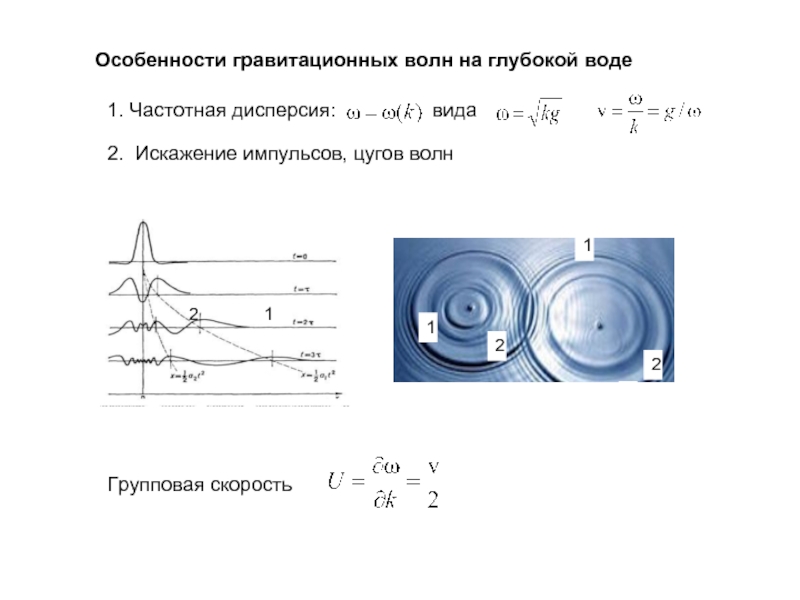
Слайд 7Особенности гравитационных волн на глубокой воде
1. Частотная дисперсия:
вида
2. Искажение импульсов,
1
2
1
2
1
Групповая скорость
2
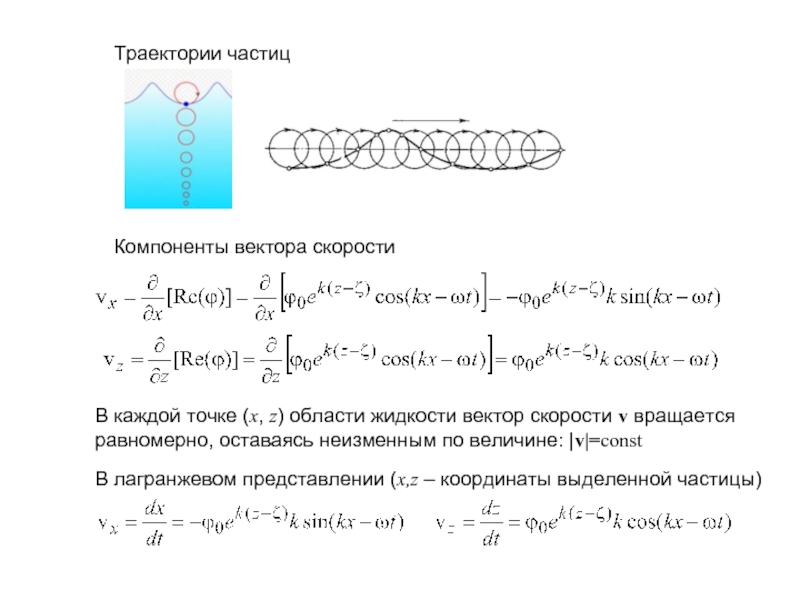
Слайд 8Траектории частиц
Компоненты вектора скорости
В каждой точке (x, z) области жидкости вектор
равномерно, оставаясь неизменным по величине: |v|=const
В лагранжевом представлении (x,z – координаты выделенной частицы)
Слайд 9Уравнения движения частицы жидкости в параметрической форме.
Показывают, что частицы жидкости в
вокруг точек окружности с радиусами, экспоненциально
уменьшающимися с удалением вглубь жидкости. При совершении еще
и равномерного горизонтального перемещения со скоростью волны v
образующаяся при кривая изображает поверхностный
профиль волны.
2. Звуковые волны
Звуковые волны – малые возмущения сжатия. Принципиально
важен учет сжимаемости среды. Уравнения гидродинамики
рассматриваются обычно с учетом адиабатической связи
Слайд 10Адиабатическая связь p(ρ) − следствие обычно быстрого протекания
акустических процессов, когда теплопередача
среды практически отсутствует
Равновесное состояние и отклонения от равновесия
В отсутствие звуковой волны жидкость характеризуют равновесными
значениями плотности и давления
Под действием звуковой волны возникают отклонения
Зависимость p=p(ρ) разлагают в ряд по этим отклонениям
В линейном приближении по малым отклонениям
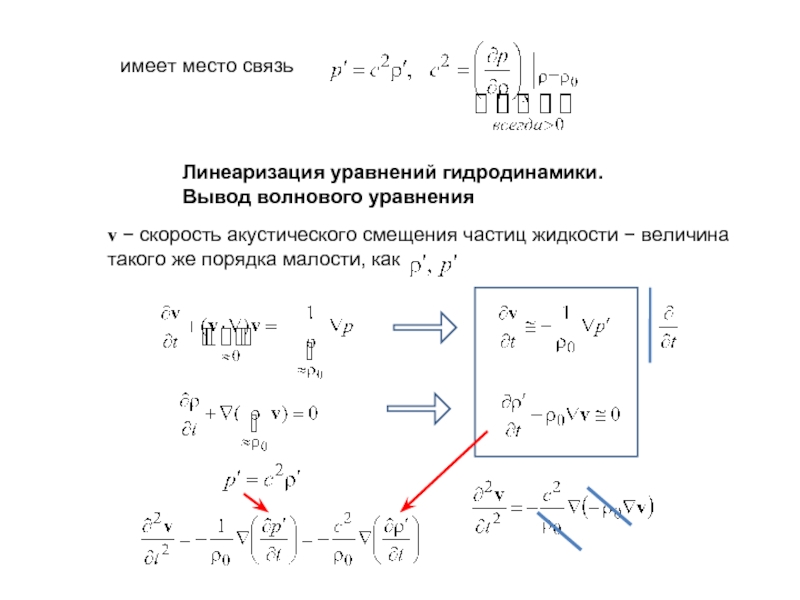
Слайд 11имеет место связь
Линеаризация уравнений гидродинамики.
Вывод волнового уравнения
v − скорость акустического
такого же порядка малости, как
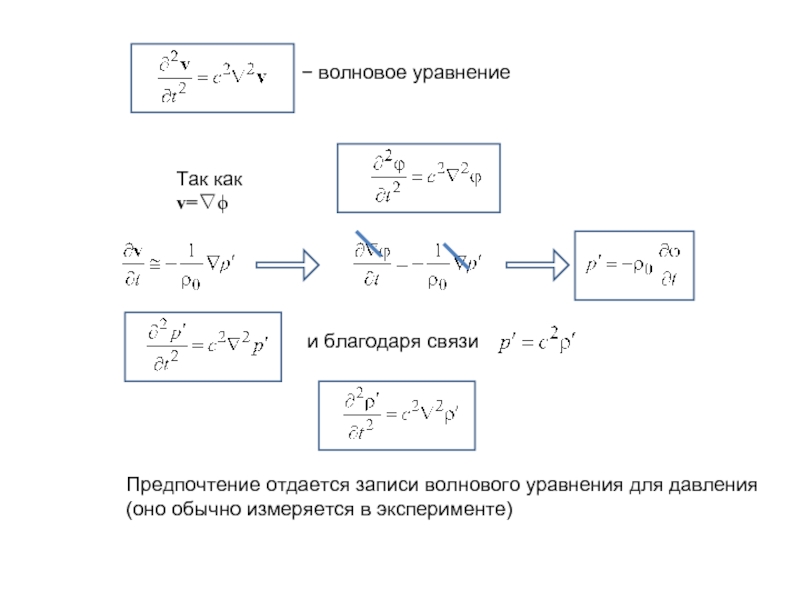
Слайд 12− волновое уравнение
Так как v=∇ϕ
и благодаря связи
Предпочтение отдается записи волнового
(оно обычно измеряется в эксперименте)
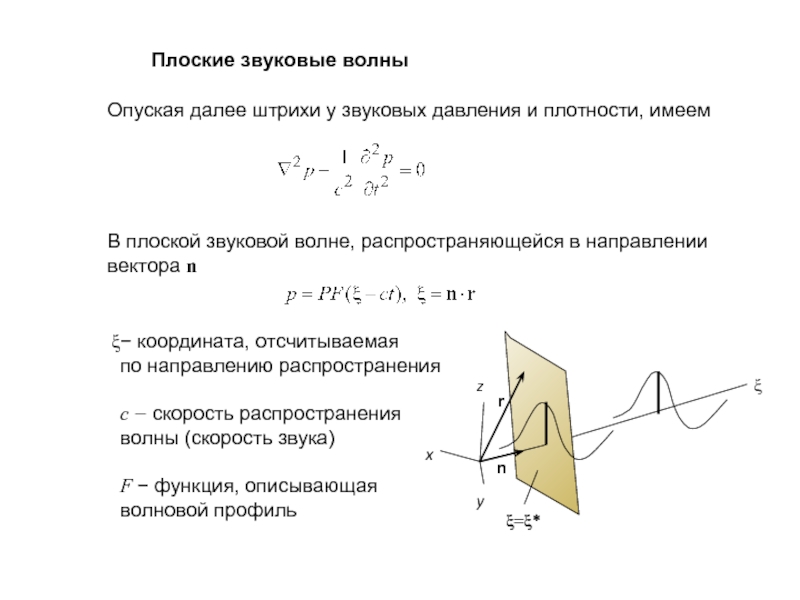
Слайд 13Плоские звуковые волны
Опуская далее штрихи у звуковых давления и плотности, имеем
В
вектора n
− координата, отсчитываемая
по направлению распространения
с − скорость распространения
волны (скорость звука)
F − функция, описывающая
волновой профиль
Слайд 14Продольность звуковых волн
Обратимся к представлению волны потенциалом
Тогда скорость частиц в волне
Отсюда:
распространения волны, т.е. звуковые волны являются
продольными.
Плоские гармонические волны
k=nk − волновой вектор, ω=kc − частота
экспоненциальная
форма записи
ω
k
0
Спектр звуковых волн в
идеальной жидкости
Слайд 15
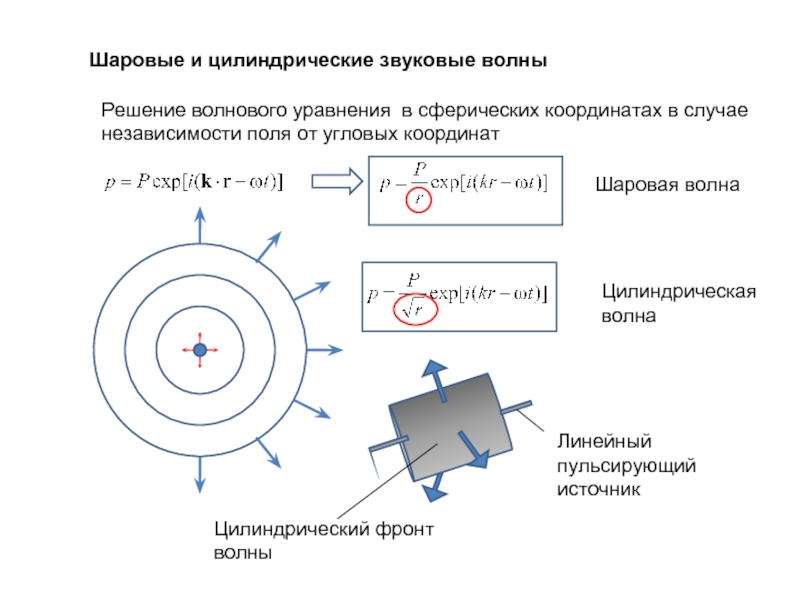
Шаровые и цилиндрические звуковые волны
Решение волнового уравнения в сферических координатах в
независимости поля от угловых координат
Цилиндрическая
волна
Шаровая волна
Линейный
пульсирующий
источник
Цилиндрический фронт
волны
Слайд 16Волновое поле колеблющегося
кварца размером в 4λ
Интерференция полей
Отражение и преломление
ультразвукового пучка на
границе «керосин-вода»
Дифракция Френеля ультразвуковой
волны на краю экрана и шаре