- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Гармоническое колебательное движение. (Лекция 6) презентация
Содержание
- 1. Гармоническое колебательное движение. (Лекция 6)
- 2. Кинематика гармонических колебаний φ = φ0 +
- 3. y = A sinφ = A sin(ωt
- 4. Динамика гармонических колебаний Свойства силы F F ~ x x>0 F
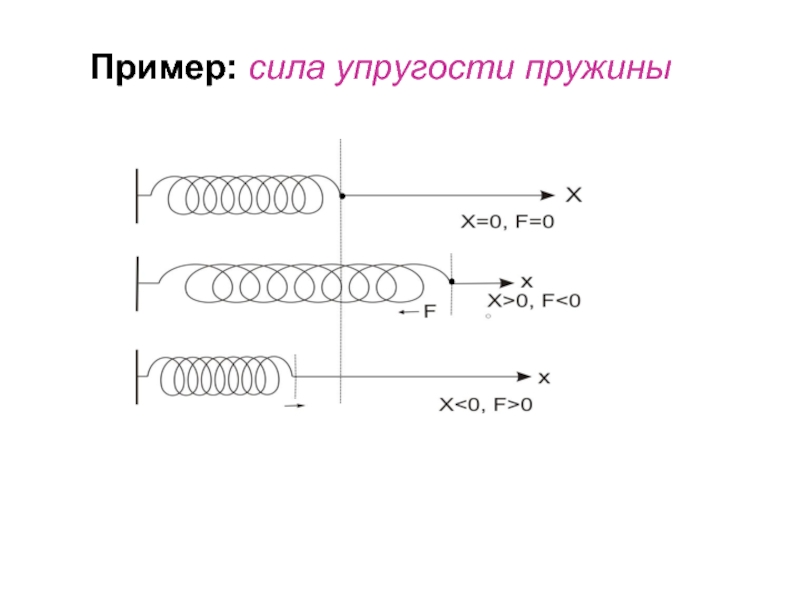
- 5. Пример: сила упругости пружины
- 6. к – коэффициент жёсткости пружины Т и
- 7. Математический маятник Составляющая силы тяжести вызывает гармонические
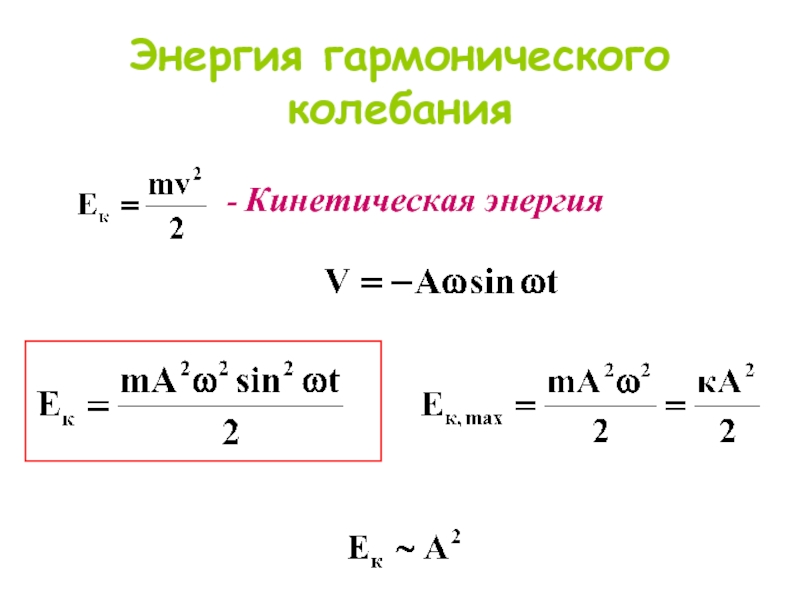
- 8. Энергия гармонического колебания Кинетическая энергия
- 9. Потенциальная энергия
- 10. Сложение колебаний одного направления х = х1
- 11. Метод векторной диаграммы по теореме косинусов х(t)
- 12. Сложение взаимноперпендикулярных колебаний Колебания происходят вдоль осей
- 13. 3) Разность фаз φ = π/2 х
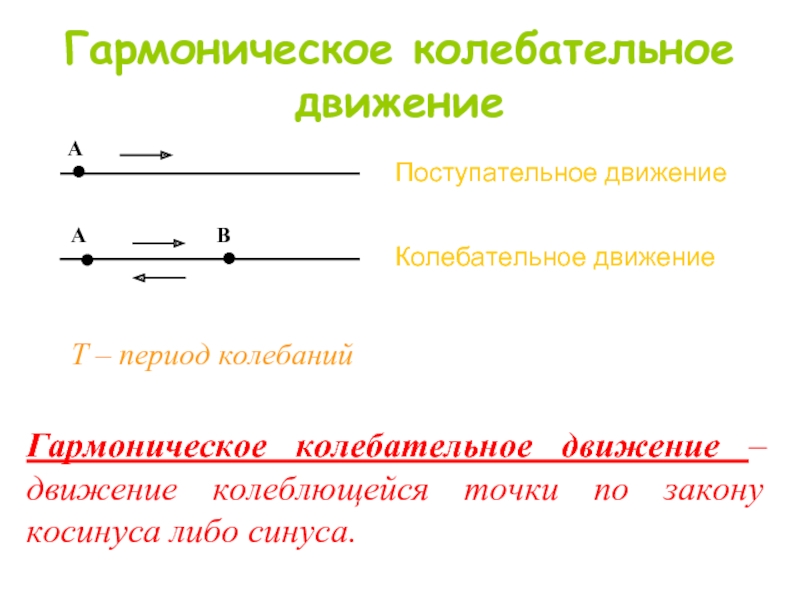
Слайд 1Гармоническое колебательное движение
Поступательное движение
Колебательное движение
Т – период колебаний
Гармоническое колебательное движение –
Слайд 2Кинематика гармонических колебаний
φ = φ0 + ωt - уравнение движения т.Д
φ =
x = A cosφ = A cos (ωt + φ0)
Уравнение гармонических колебаний
x – смещение
|A| – амплитуда колебаний
φ – фаза колебаний
φ0 – начальная фаза (t = 0)
ω – круговая частота
- период колебаний
;
Слайд 3y = A sinφ = A sin(ωt + φ0)
Уравнение гармонических колебаний
x
v – скорость гармонических колебаний точки
а – ускорение гармонических колебаний точки
(φ0 = 0)
Векторная диаграмма гармонического колебания
Слайд 4Динамика гармонических колебаний
Свойства силы F
F ~ x
x>0 F
- сила, вызывающая гармонические колебания
Слайд 6к – коэффициент жёсткости пружины
Т и ω не зависят от A
Т
F = - к х
Сила, подчиняющаяся этому закону, но не являющаяся упругой, называется «квазиупругой».
Упругие и «квазиупругие» силы вызывают гармонические колебания.
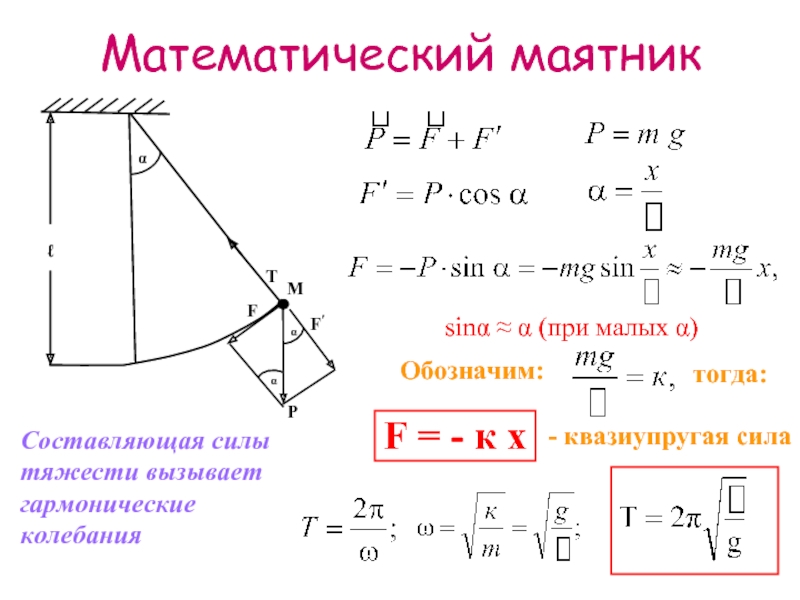
Слайд 7Математический маятник
Составляющая силы тяжести вызывает гармонические колебания
sinα ≈ α (при малых
Обозначим:
тогда:
F = - к х
- квазиупругая сила
Слайд 10Сложение колебаний одного направления
х = х1 + х2 – результирующее колебание
А1, А2 – амплитуды складываемых колебаний
φ1, φ2 – начальные фазы
Используется метод векторной диаграммы
Слайд 11Метод векторной диаграммы
по теореме косинусов
х(t) = A cos (ω0t +φ) Суммарное
Слайд 12Сложение взаимноперпендикулярных колебаний
Колебания происходят вдоль осей х и у с одинаковой
Пусть начальная фаза колебания вдоль оси х равна нулю.
(1) х = А cos ωt φ – разность фаз колебаний
(2) y = B cos (ωt+φ) A и B – амплитуда складываемых колебаний
Уравнение траектории колеблющейся точки y = y (x).
Разность фаз φ = 0
Из (1) и (2) находим
2) Разность фаз φ = π
Траектория точки, также прямая (пунктир на рисунке)
Слайд 133) Разность фаз φ = π/2
х = А cos ωt
y =
Уравнение эллипса
А
Если А=В, то эллипс вырождается в окружность