- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Фундаментальные отношения между пикселами презентация
Содержание
- 1. Фундаментальные отношения между пикселами
- 2. Соседи отдельного элемента N4(p) (x+1,y), (x-1,y), (x,y+1),
- 3. Смежность V – множество значений яркости. p,q
- 4. Дискретным путем от p(x,y) до q(s,t) называется
- 5. Пусть R – некоторое подмножество элементов изображения.
- 6. p(x,y), q(s,t), z(v,w). Функция расстояния D: D(p,q)
- 7. Евклидово расстояние (l2): Расстояние D4
- 8. Поэлементные и матричные операции
- 9. Линейный оператор H Сумма изображений
- 10. Арифметические операции
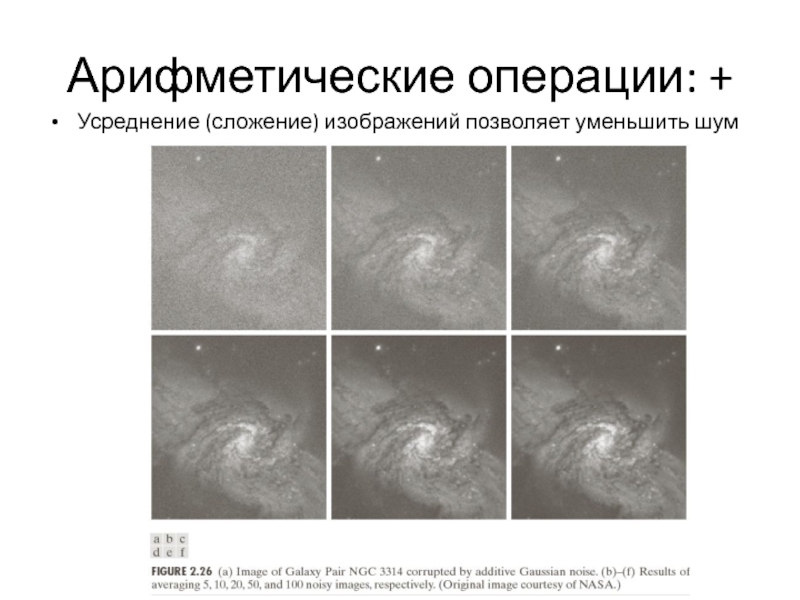
- 11. Усреднение (сложение) изображений позволяет уменьшить шум Арифметические операции: +
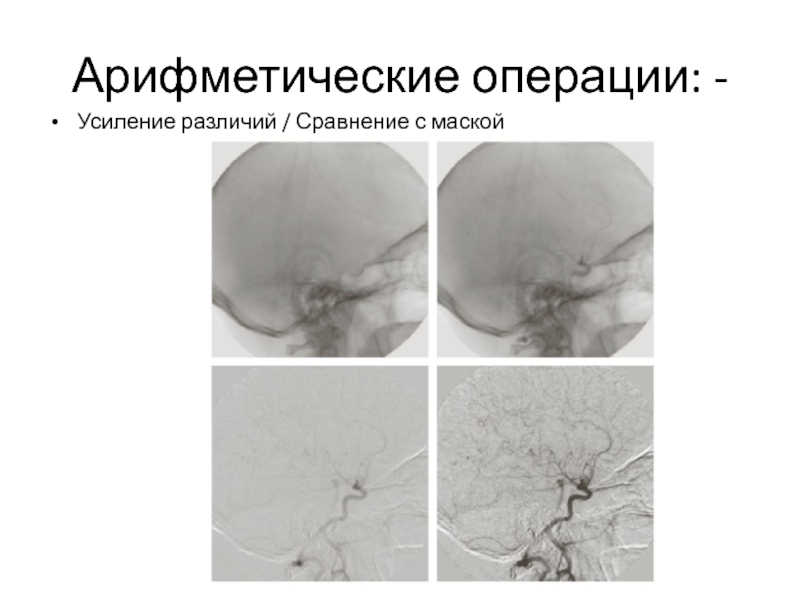
- 12. Усиление различий / Сравнение с маской Арифметические операции: -
- 13. Определение движения Арифметические операции: -
- 14. Коррекция затенений Арифметические операции: *
- 15. Выделение требуемой области Арифметические операции: *
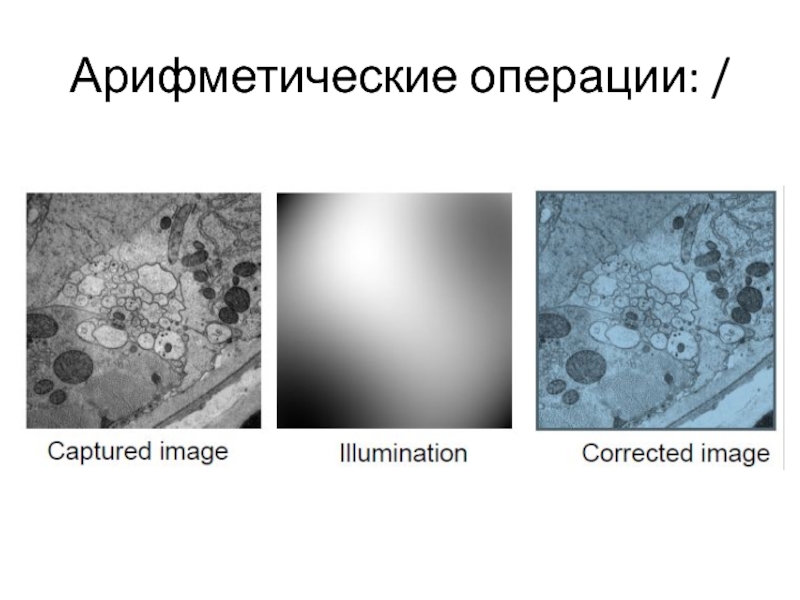
- 16. Арифметические операции: /
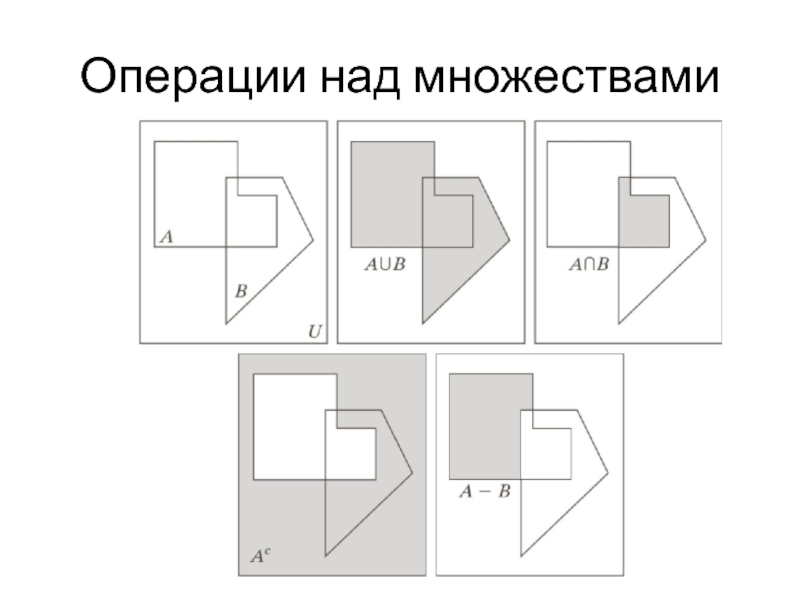
- 17. Операции над множествами
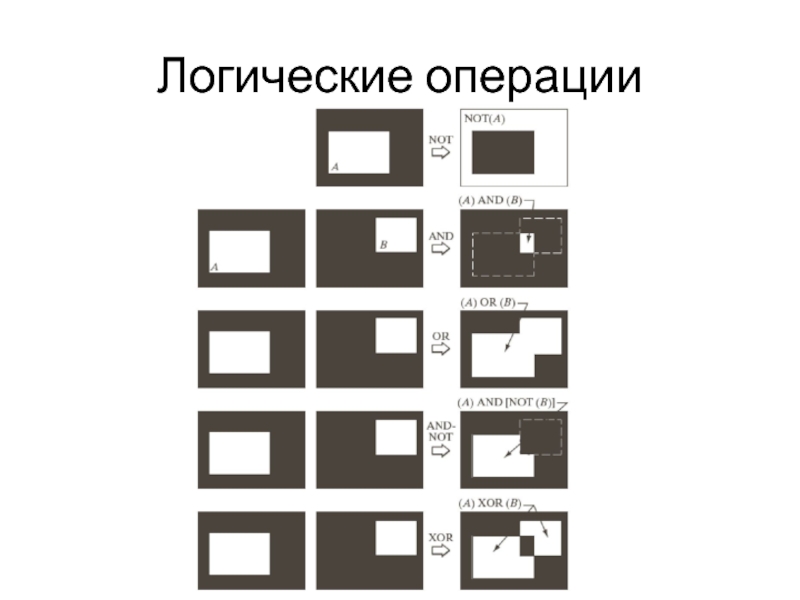
- 18. Логические операции
- 19. Логические операции
Соседи отдельного элемента N4(p) (x+1,y), (x-1,y), (x,y+1), (x,y-1) ND(p) (x+1,y+1), (x+1,y-1), (x-1,y+1), (x-1,y-1) N8(p) p = p(x,y)
Слайд 2Соседи отдельного элемента
N4(p)
(x+1,y), (x-1,y), (x,y+1), (x,y-1)
ND(p)
(x+1,y+1), (x+1,y-1), (x-1,y+1), (x-1,y-1)
N8(p)
p = p(x,y)
Слайд 3Смежность
V – множество значений яркости. p,q из V.
4-смежность
q в N4(p)
8-смежность
q
в N8(p)
m-смежность
а) q в N4(p), или
б) q в ND(p), N4(p) и N4(q)
не содержит элементов из V
m-смежность
а) q в N4(p), или
б) q в ND(p), N4(p) и N4(q)
не содержит элементов из V
Слайд 4Дискретным путем от p(x,y) до q(s,t) называется неповторяющаяся последовательность пикселей
(x0,y0),
(x1,y1), ... ,(xn,yn),
где (x0,y0)=(x,y), (xn,yn)=(s,t), и
(xi,yi) и (xi-1,yi-1) – являются смежными.
где (x0,y0)=(x,y), (xn,yn)=(s,t), и
(xi,yi) и (xi-1,yi-1) – являются смежными.
Область и граница
Пусть S – некоторое подмножество элементов изображения. Два элемента называются связными в S, если между ними существует путь, целиком состоящий из элементов S. Множество всех элементов, связанных с данным, называют компонентой связности. Связное множество – множество, содержащее только одну компоненту связности.
Слайд 5Пусть R – некоторое подмножество элементов изображения. Будем называть его областью,
если R – связное множество. Границей области R называется множество пикселей этой области, у которых один или более соседей не являются элементами R.
Область и граница
Слайд 6p(x,y), q(s,t), z(v,w). Функция расстояния D:
D(p,q) ≥ 0, причем D(p,q) =
0 ↔ p = q
D(p,q) = D(q,p)
D(p,z) ≤ D(p,q) + D(q,z)
расстояние между двумя изображениями определяется через норму Гёльдера, усредненную на количество элементов изображения
при p=1 возникает средняя разность, а при p=2 – корень из среднеквадратического отклонения (RMSE).
На основе введенного расстояния строится пиковое отношение сигнал/шум (PSNR) между двумя изображениями
D(p,q) = D(q,p)
D(p,z) ≤ D(p,q) + D(q,z)
расстояние между двумя изображениями определяется через норму Гёльдера, усредненную на количество элементов изображения
при p=1 возникает средняя разность, а при p=2 – корень из среднеквадратического отклонения (RMSE).
На основе введенного расстояния строится пиковое отношение сигнал/шум (PSNR) между двумя изображениями
Меры расстояния
Слайд 9Линейный оператор H
Сумма изображений
Нелинейный оператор max
Линейные и нелинейные преобразования
