- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Фраунгофер дифракциясы. Дифракциялық тор және оның спектрлік сипаттамасы. Дифракция және спектрлік талдау. Майкельсон эшелоны презентация
Содержание
- 1. Фраунгофер дифракциясы. Дифракциялық тор және оның спектрлік сипаттамасы. Дифракция және спектрлік талдау. Майкельсон эшелоны
- 2. Шексіз ұзын, ені b саңылауға
- 3. Саңлаудан кейін линза, ал оның тоғыстық жазықтығына
- 4. Түсетін толқын бағытымен ϕ бұрыш (дифракция бұрышы)
- 5. Осы жазықтықта орын алатын фазалардың үлестірілуі Bϕ
- 6. 1-суреттен А нүктесіне (аумақтың сол жақ шеті)
- 7. Саңылаудың ортасында жататын нүкте үшін (линзаның центріне
- 8. Егер (2) болған
- 9. Негізгі жарық ағыны
- 10. Максимумдар мен минимумдардың орны λ толқын ұзындығына
- 11. Орталық максимум (ϕ=0) барлық толқын ұзындықтары үшін
- 12. Дифракциялық тор – жарықты спектрге бөлетін және
- 13. Біз дифракциялық элементтері ені а мөлдір емес
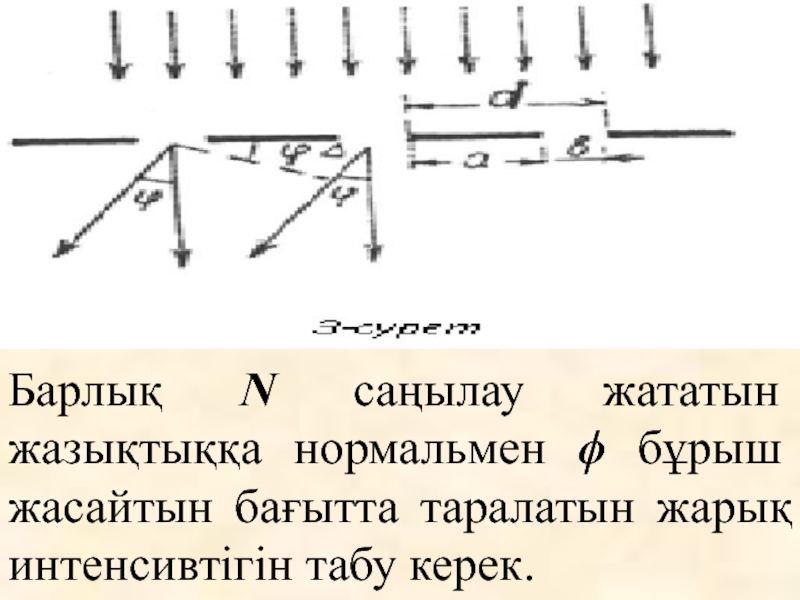
- 14. Барлық
- 15. Саңылаулардан шығатын толқындар когерентті болады, сондықтан бұлардың
- 16. Көп жарық шоқтарының көп саны интерференцияланғанда
- 17. Егер тордағы саңылаулар саны N-ге тең болса,
- 18. Осы минимумдер бір саңылаудан алынатын
- 19. Дифракциялық торларды металдық немесе әйнектен жасайды. Мөлдір
- 20. Саңылаулардың енін b әрпімен, екі саңылаудың
- 21. Максимум шартымен анықталатын бағытта интенсивтігі N2 максимумдар
- 22. В каждой точке экрана производится суммирование развернутых
- 23. Число m называют дифракционным порядком
- 24. Дифракционные решетки обладают диспергирующими свойствами, разводя лучи,
- 25. m=1 m=2 m=3 m=4 m=5 m=6
- 26. Наклонное падение света В случае наклонного падения
- 27. Помимо амплитудных решеток, работающих на пропускание или
- 28. создаются путем нанесения треугольного профиля, образующего на
- 29. Синусоидальная решётка Особое значение имеет дифракция на
- 30. Для двумерной дифракционной решетки в двух ортогональных
- 31. 1. Объект-двумерная решетка 2. Фурье-образ объекта 3.
- 32. а) объект MIPT (MIPT-Moscow Institute of Physics
- 33. Каждый пиксель в новом дисплее должен представлять
Слайд 1 Жарық дифракциясы Лекция – 6 Фраунгофер дифракциясы. Дифракциялық тор және оның спектрлік сипаттамасы.
Слайд 2 Шексіз ұзын, ені b саңылауға жазық жарық толқыны нормаль (тік) түсетін
Слайд 3Саңлаудан кейін линза, ал оның тоғыстық жазықтығына L бақылау қалқасы қойылған.
Слайд 4Түсетін толқын бағытымен ϕ бұрыш (дифракция бұрышы) жасайтын бағытында саңылаудың түгелдей
Слайд 5Осы жазықтықта орын алатын фазалардың үлестірілуі Bϕ нүктесіне дейін келіп жететін
Слайд 61-суреттен А нүктесіне (аумақтың сол жақ шеті) және А нүктесінен х
Слайд 7Саңылаудың ортасында жататын нүкте үшін (линзаның центріне қарсы нүкте) дифракция бұрышы
Слайд 8Егер (2) болған жағдайда Аϕ амплитуда нөлге айналады.
Слайд 9Негізгі жарық ағыны
Слайд 10Максимумдар мен минимумдардың орны λ толқын ұзындығына тәуелді. Дифракциялық суреттің түрі
Слайд 11Орталық максимум (ϕ=0) барлық толқын ұзындықтары үшін ортақ болады, осыдан дифракциялық
Слайд 12Дифракциялық тор – жарықты спектрге бөлетін және жарықтың толқын ұзындығын өлшеуге
Слайд 13Біз дифракциялық элементтері ені а мөлдір емес аралықтармен бөлінген ені b
Слайд 14 Барлық N саңылау жататын жазықтыққа нормальмен ϕ бұрыш жасайтын бағытта таралатын
Слайд 15Саңылаулардан шығатын толқындар когерентті болады, сондықтан бұлардың араларындағы интерференцияны ескеру керек
Слайд 16Көп жарық шоқтарының көп саны интерференцияланғанда
Слайд 17Егер тордағы саңылаулар саны N-ге тең болса, онда бас максимумдар араларына
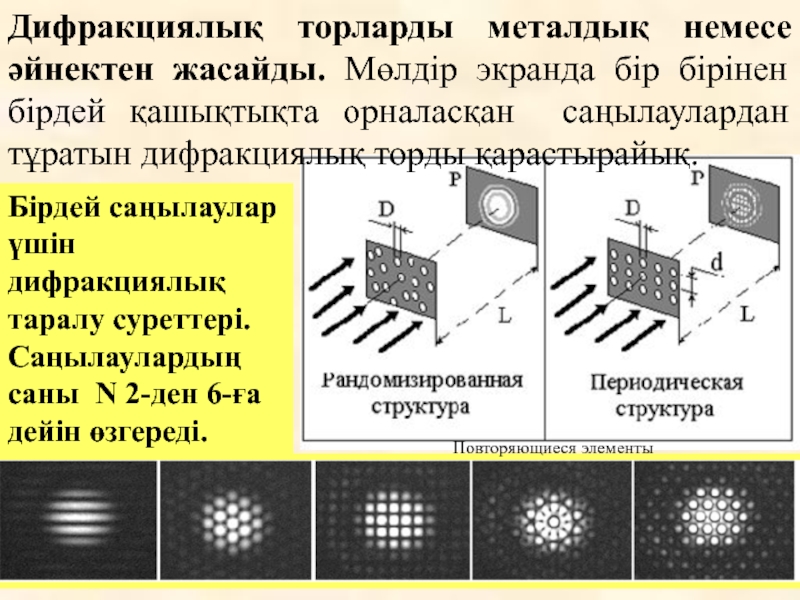
Слайд 19Дифракциялық торларды металдық немесе әйнектен жасайды. Мөлдір экранда бір бірінен бірдей
Бірдей саңылаулар үшін дифракциялық таралу суреттері. Саңылаулардың саны N 2-ден 6-ға дейін өзгереді.
Повторяющиеся элементы
Слайд 20
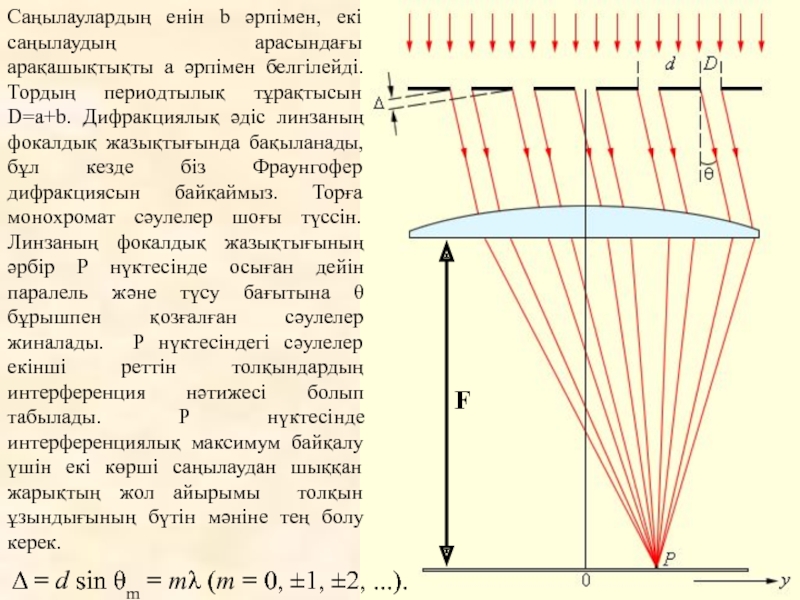
Саңылаулардың енін b әрпімен, екі саңылаудың арасындағы арақашықтықты а әрпімен белгілейді.
F
Δ = d sin θm = mλ (m = 0, ±1, ±2, ...).
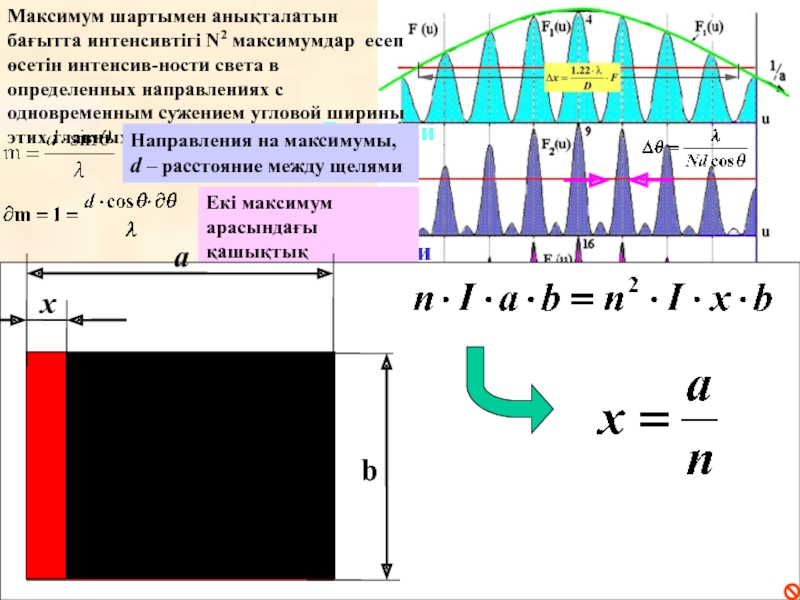
Слайд 21Максимум шартымен анықталатын бағытта интенсивтігі N2 максимумдар есеп өсетін интенсив-ности света
Если прозрачность транспаранта описывается периодической функцией типа:
То её Фурье образ описывается функцией:
Две щели
Три щели
Четыре щели
8 щелей
Направления на максимумы, d – расстояние между щелями
Екі максимум арасындағы қашықтық
Полуширина одного главного максимума дифракционной решётки
b
x
а
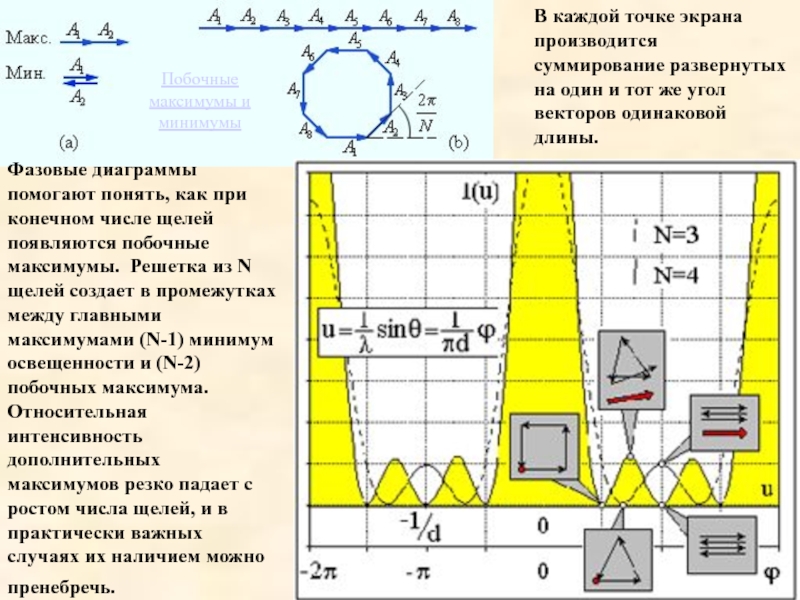
Слайд 22В каждой точке экрана производится суммирование развернутых на один и тот
Фазовые диаграммы помогают понять, как при конечном числе щелей появляются побочные максимумы. Решетка из N щелей создает в промежутках между главными максимумами (N-1) минимум освещенности и (N-2) побочных максимума. Относительная интенсивность дополнительных максимумов резко падает с ростом числа щелей, и в практически важных случаях их наличием можно пренебречь.
Побочные максимумы и минимумы
Слайд 23
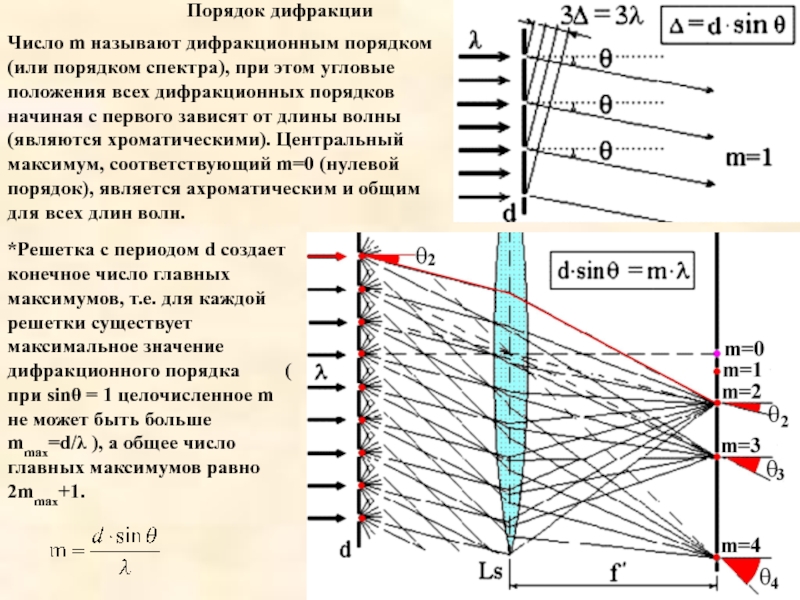
Число m называют дифракционным порядком (или порядком спектра), при этом угловые
*Решетка с периодом d создает конечное число главных максимумов, т.е. для каждой решетки существует максимальное значение дифракционного порядка ( при sinθ = 1 целочисленное m не может быть больше mmax=d/λ ), а общее число главных максимумов равно 2mmax+1.
Порядок дифракции
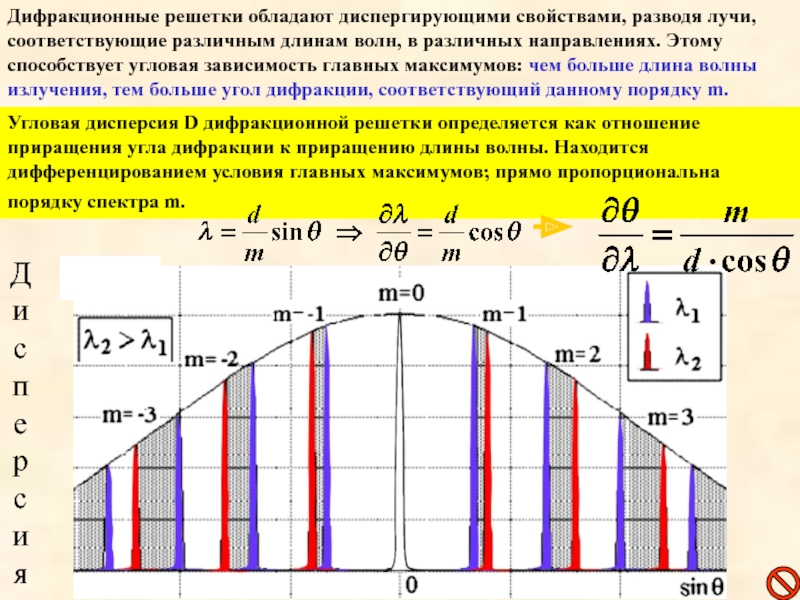
Слайд 24Дифракционные решетки обладают диспергирующими свойствами, разводя лучи, соответствующие различным длинам волн,
Угловая дисперсия D дифракционной решетки определяется как отношение приращения угла дифракции к приращению длины волны. Находится дифференцированием условия главных максимумов; прямо пропорциональна порядку спектра m.
Дисперсия
Слайд 25m=1
m=2
m=3
m=4
m=5
m=6
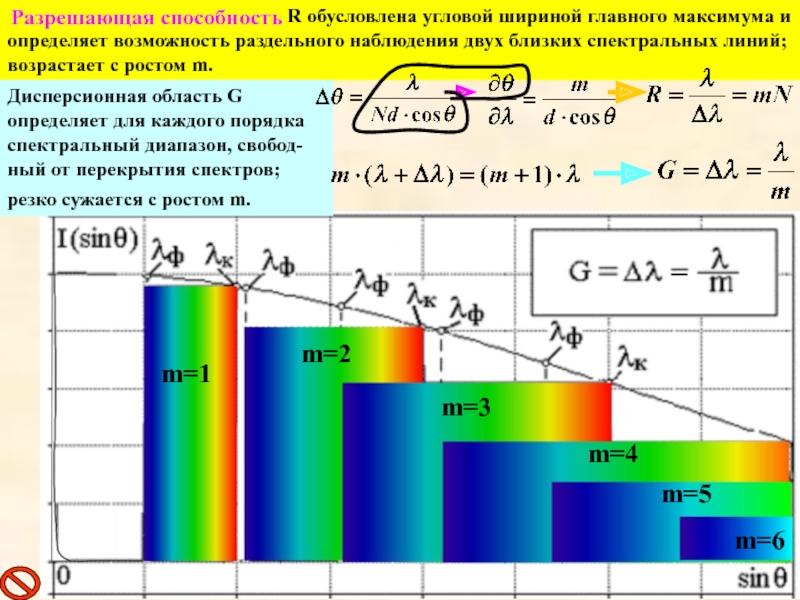
Дисперсионная область G определяет для каждого порядка спектральный диапазон, свобод-ный от перекрытия спектров; резко сужается с ростом m.
Разрешающая способность
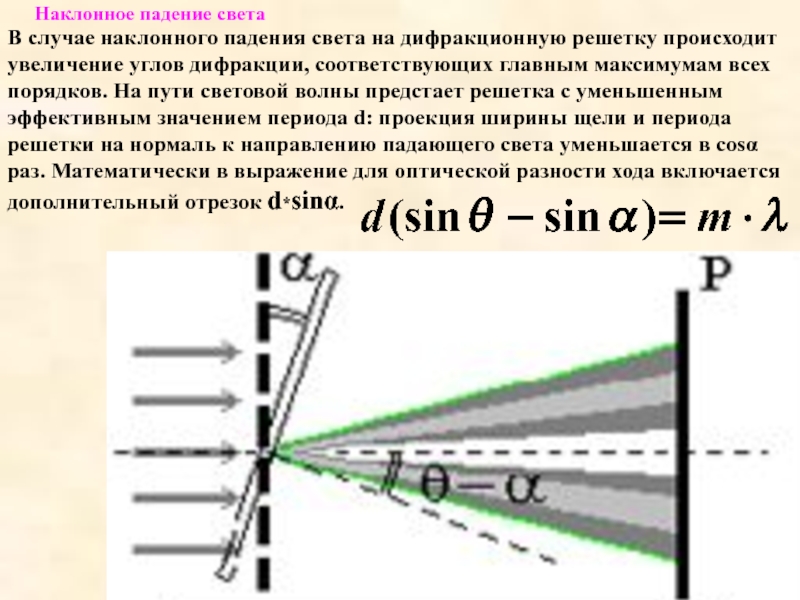
Слайд 26Наклонное падение света
В случае наклонного падения света на дифракционную решетку происходит
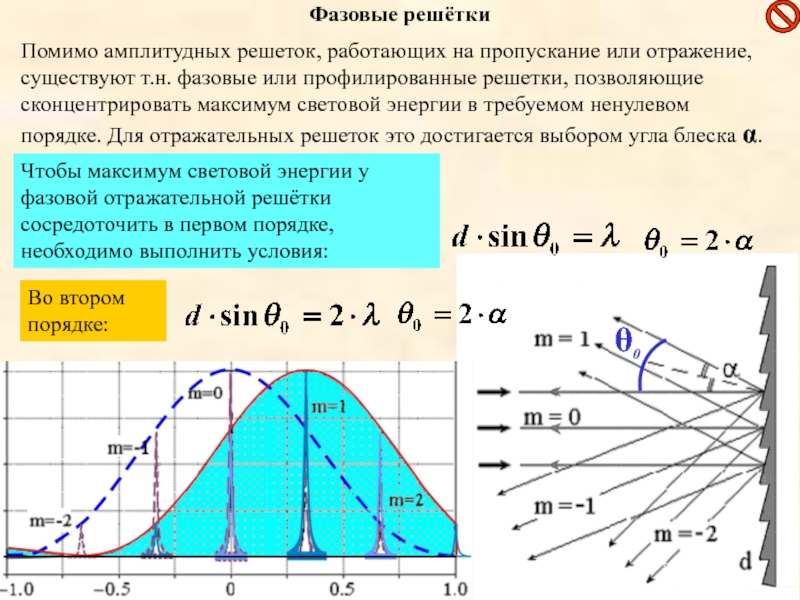
Слайд 27Помимо амплитудных решеток, работающих на пропускание или отражение, существуют т.н. фазовые
Чтобы максимум световой энергии у фазовой отражательной решётки сосредоточить в первом порядке, необходимо выполнить условия:
θ0
Во втором порядке:
Фазовые решётки
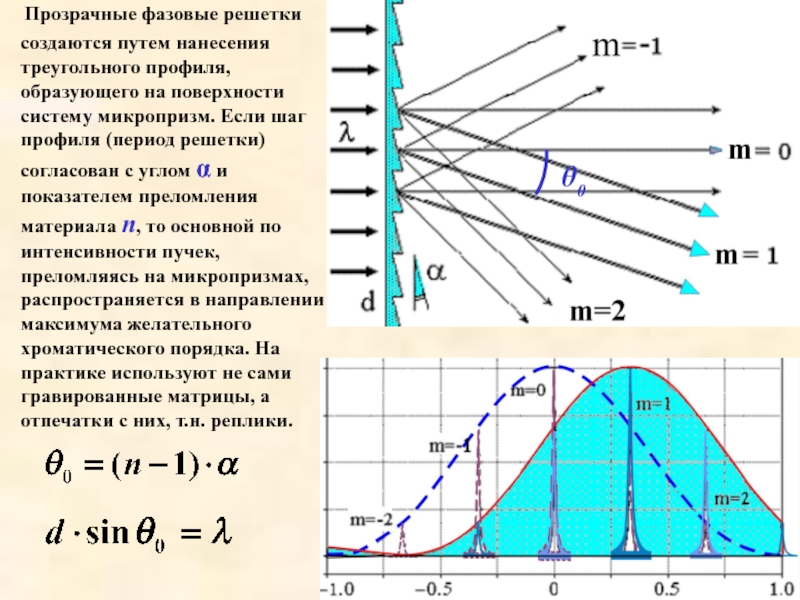
Слайд 28создаются путем нанесения треугольного профиля, образующего на поверхности систему микропризм. Если
Прозрачные фазовые решетки
θ0
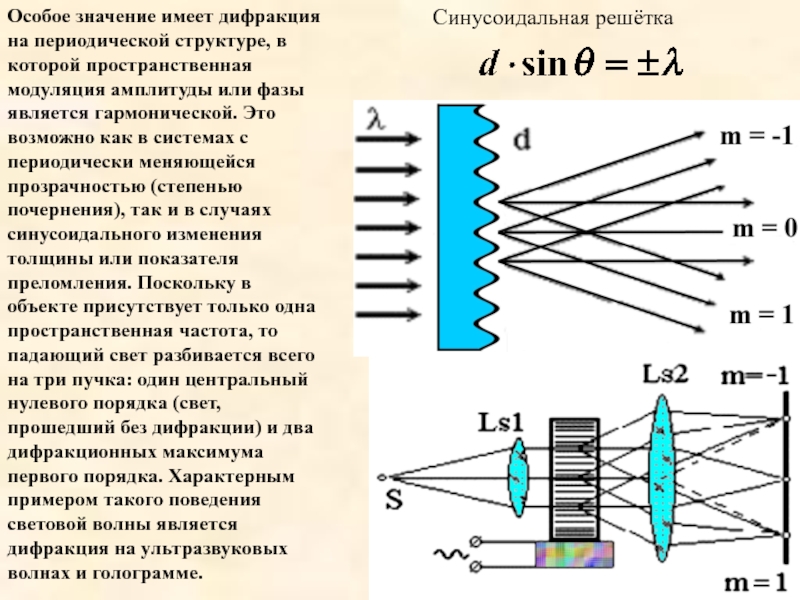
Слайд 29Синусоидальная решётка
Особое значение имеет дифракция на периодической структуре, в которой пространственная
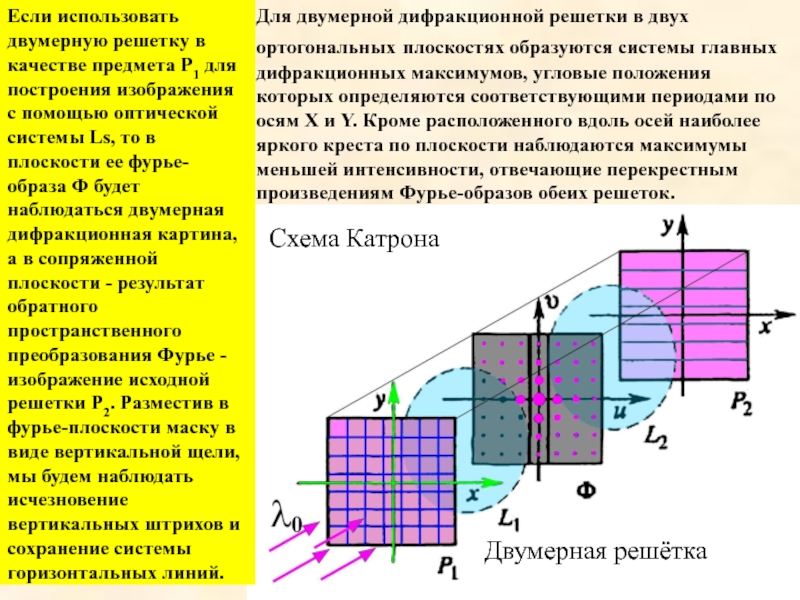
Слайд 30Для двумерной дифракционной решетки в двух ортогональных плоскостях образуются системы главных
Если использовать двумерную решетку в качестве предмета Р1 для построения изображения с помощью оптической системы Ls, то в плоскости ее фурье-образа Ф будет наблюдаться двумерная дифракционная картина, а в сопряженной плоскости - результат обратного пространственного преобразования Фурье - изображение исходной решетки Р2. Разместив в фурье-плоскости маску в виде вертикальной щели, мы будем наблюдать исчезновение вертикальных штрихов и сохранение системы горизонтальных линий.
Двумерная решётка
Схема Катрона
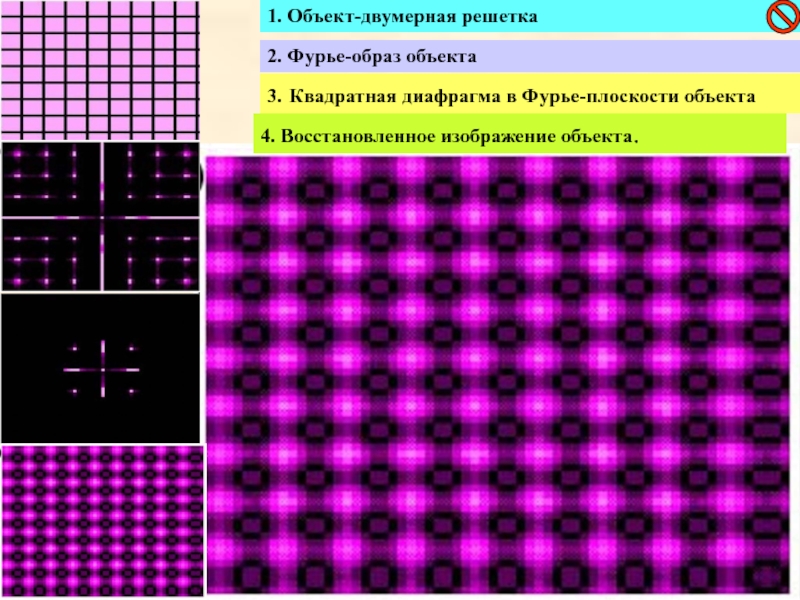
Слайд 311. Объект-двумерная решетка
2. Фурье-образ объекта
3. Квадратная диафрагма в Фурье-плоскости объекта
4. Восстановленное
Слайд 32а) объект MIPT (MIPT-Moscow Institute of Physics and Technology);
b) его
с) объект - буква Р;
d) его Фурье-образ;
е) результат вычитания Ф-образов b) и d);
f) восстановленное изображение.
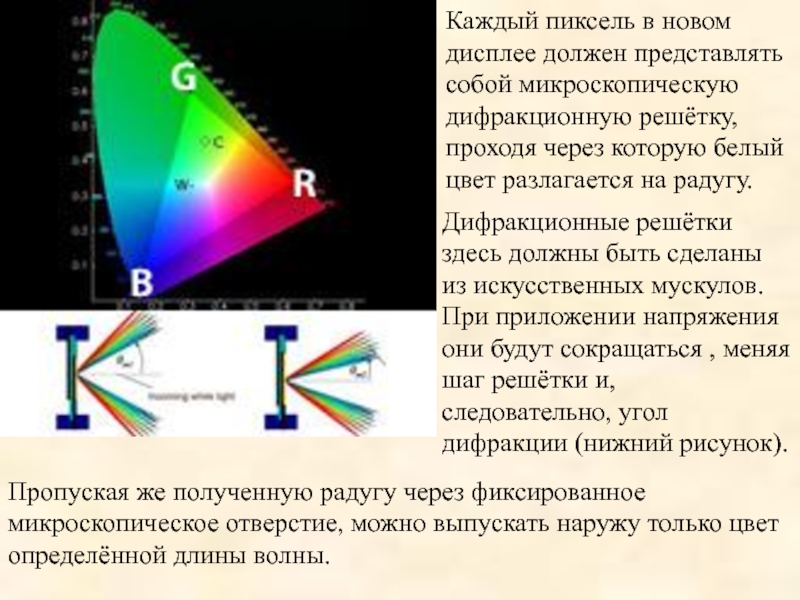
Слайд 33Каждый пиксель в новом дисплее должен представлять собой микроскопическую дифракционную решётку,
Дифракционные решётки здесь должны быть сделаны из искусственных мускулов. При приложении напряжения они будут сокращаться , меняя шаг решётки и, следовательно, угол дифракции (нижний рисунок).
Пропуская же полученную радугу через фиксированное микроскопическое отверстие, можно выпускать наружу только цвет определённой длины волны.