и релятивистской механики
6 лекций
(12 аудиторных часов)
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема 1,Кинет. пост., лекция 1, версия 3 презентация
Содержание
- 1. Тема 1,Кинет. пост., лекция 1, версия 3
- 2. Раздел 1. Классическая механика Темы лекций
- 3. Тема 1. Кинематика поступательного движения План лекции
- 4. 1.1. Основные понятия кинематики Механическое движение –
- 5. Классическую механику создал И. Ньютон.
- 6. Абсолютное пространство - трехмерно (имеет три
- 7. Абсолютное время одномерно (имеет одно
- 8. В начале ХХ века классическая механика подверглась
- 9. Теория относительности установила следующие положения о пространстве
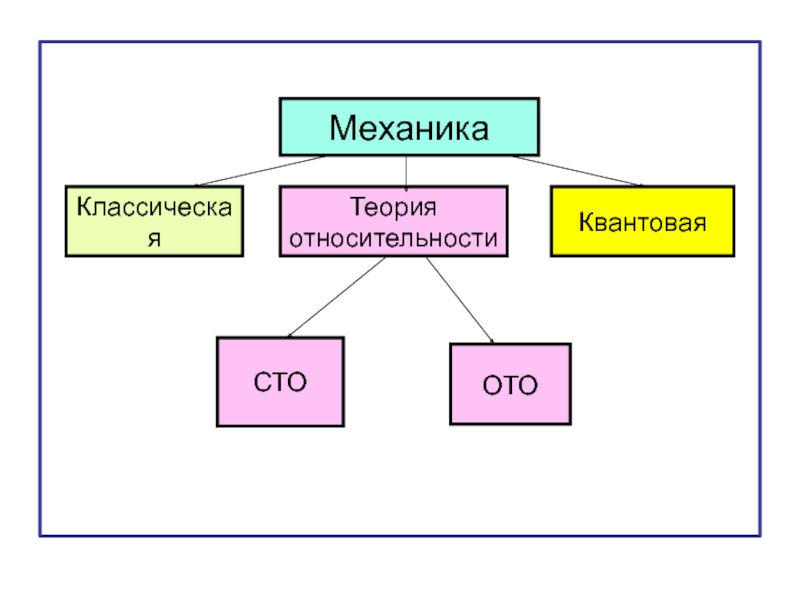
- 10. Механика Классическая Квантовая Теория относительности СТО ОТО
- 11. Классическая механика изучает макроскопические тела, движущиеся с
- 12. Механика состоит из трех разделов – кинематики,
- 13. Основные понятия механики Движение – изменение положения
- 14. 1.2. Перемещение, скорость, ускорение Описать движение материальной
- 15. Поступательным движением твёрдого тела называется движение, при
- 16. Перемещение Радиус-вектор -
- 17. Спроецируем радиус-вектор на
- 19. Траекторией называется линия: которую описывает конец радиус-вектора
- 20. Законом движения материальной точки называется уравнение, выражающее
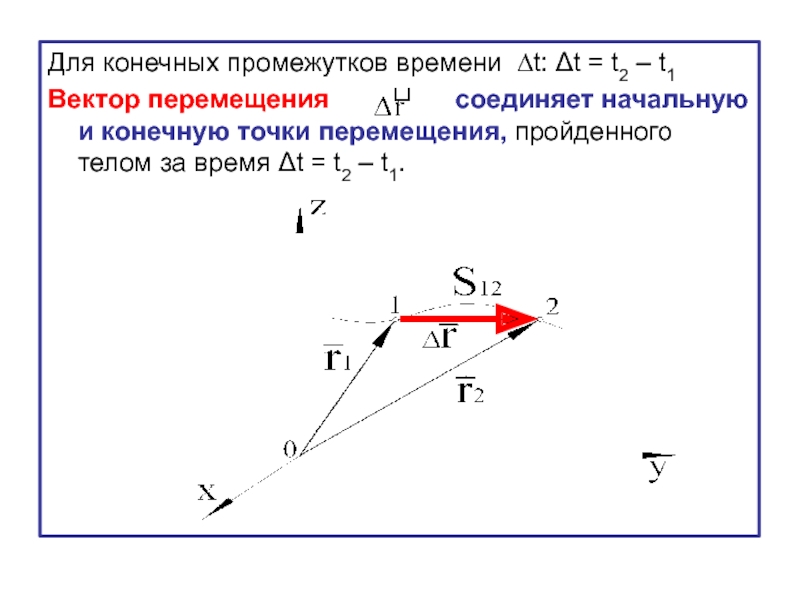
- 21. Для конечных промежутков времени ∆t: Δt =
- 23. Для бесконечно малого промежутка времени dt:
- 25. Вектор перемещения получим, просуммировав векторы элементарных перемещений:
- 27. Скорость - равна перемещению, совершенному материальной точкой
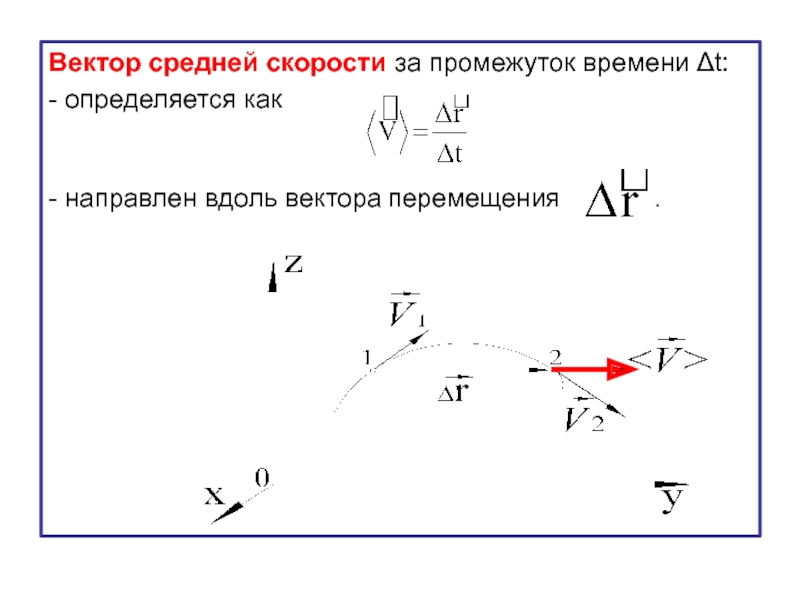
- 28. Вектор средней скорости за промежуток времени Δt:
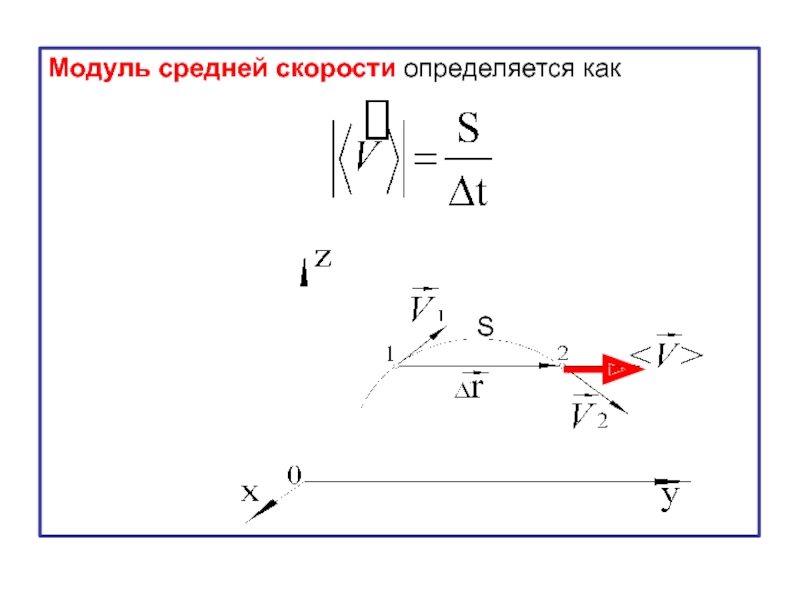
- 29. Модуль средней скорости определяется как
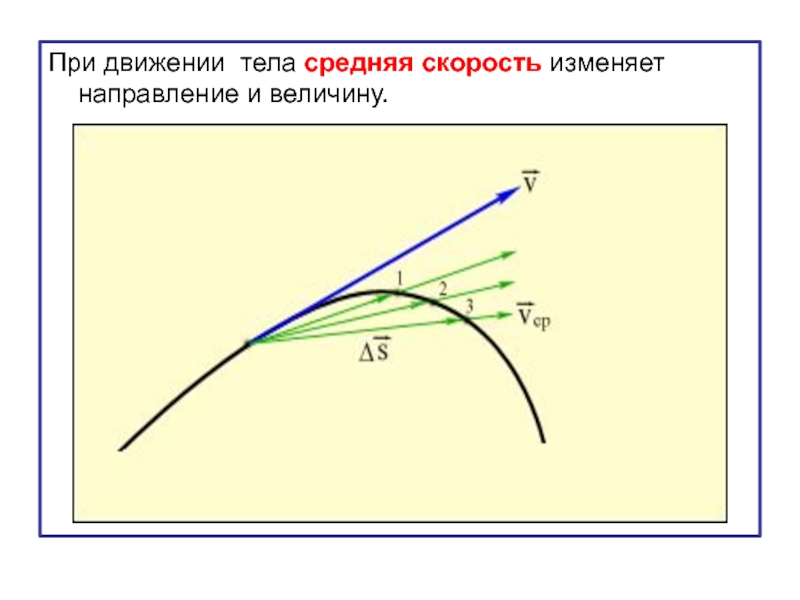
- 30. При движении тела средняя скорость изменяет направление и величину.
- 31. Мгновенная скорость равна пределу, к которому стремится
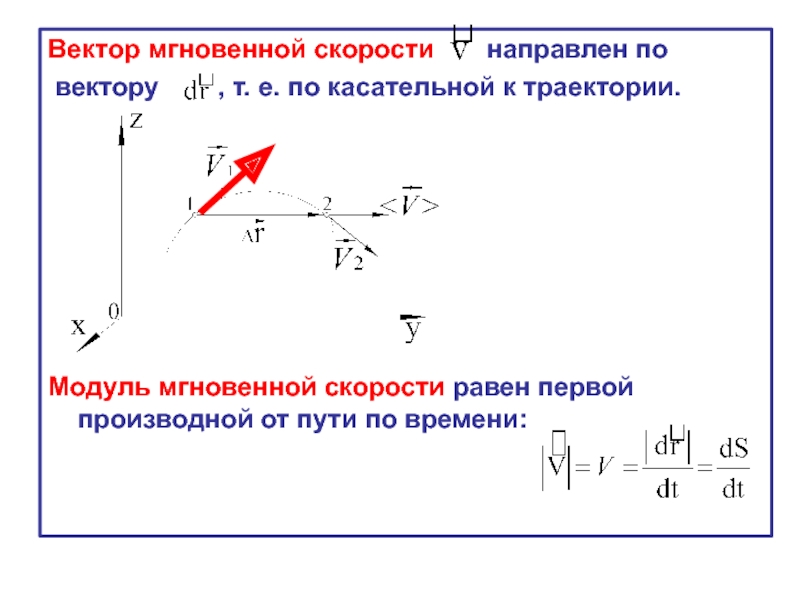
- 32. Вектор мгновенной скорости направлен
- 33. Проекции скорости на координатные оси равны первым
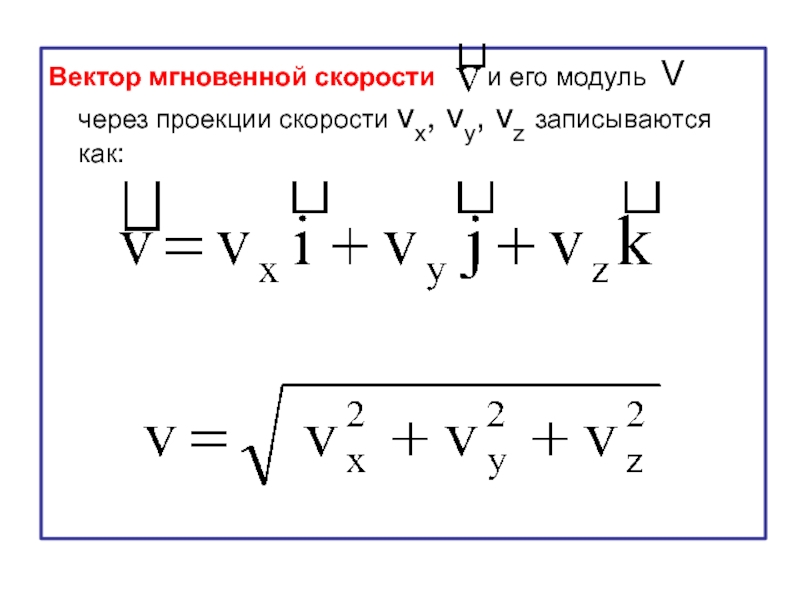
- 34. Вектор мгновенной скорости и
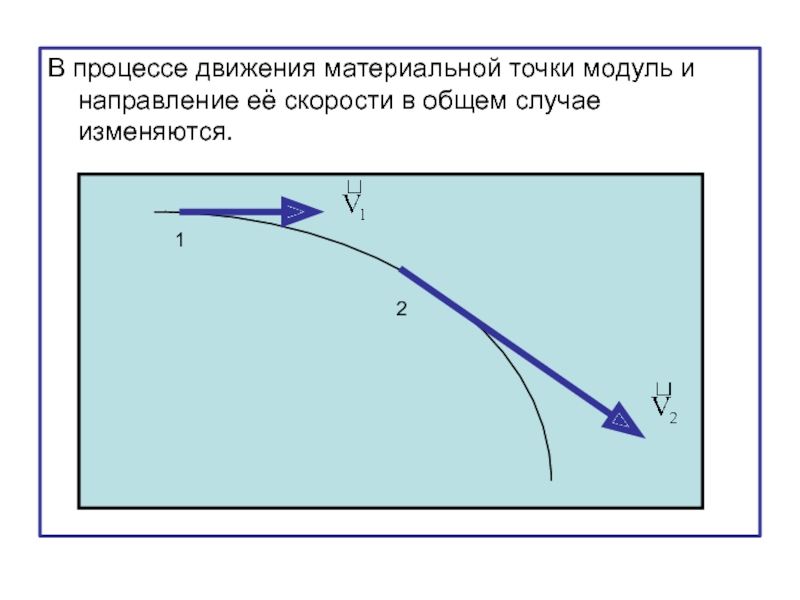
- 35. В процессе движения материальной точки модуль и
- 36. Ускорение - равно изменению скорости за единицу
- 38. Вектор среднего ускорения за промежуток времени Δt
- 39. Мгновенное ускорение равно пределу, к которому стремится
- 40. Вектор мгновенного ускорения по отношению к вектору
- 41. Если угол - острый,
- 42. Проекции вектора ускорения на координатные оси равны
- 43. Вектор мгновенного ускорения
- 44. 1.3. Обратная задача кинематики В рамках кинематики
- 45. При решении обратной задачи по известной зависимости
- 46. Из определения ускорения имеем
- 47. Окончательно скорость получим при решении данного выражения.
- 49. Частные случаи Равномерное прямолинейное движение (ускорение
- 50. Равнопеременное прямолинейное движение (ускорение
- 51. Полученное выражение, спроецированное на ось Х, имеет вид:
- 52. 1.4. Тангенциальное и нормальное ускорения Пусть материальная
- 53. Вектор ускорения можно разложить
- 54. Тангенциальное ускорение: характеризует изменение скорости по модулю;
- 55. Нормальное ускорение характеризует изменение скорости по
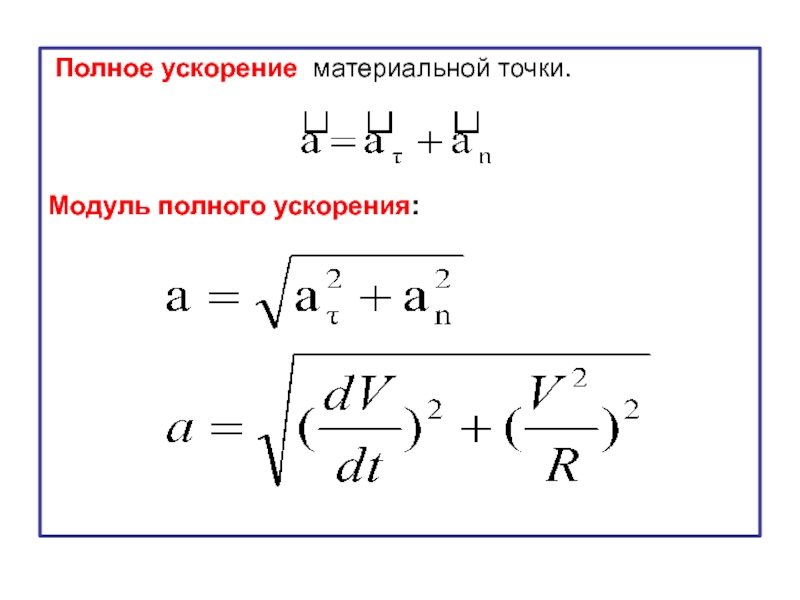
- 56. Полное ускорение материальной точки.
- 57. Частные случаи движений =
Раздел 1.
Классическая механика Темы лекций Кинематика поступательного движения. Кинематика вращательного движения. Динамика поступательного движения. Динамика вращательного движения. Работа, энергия. Законы сохранения.
Слайд 1Омский государственный технический университет
Кафедра физики
Калистратова Л.Ф.
Электронные лекции по разделам классической
Слайд 2Раздел 1.
Классическая механика
Темы лекций
Кинематика поступательного движения.
Кинематика вращательного движения.
Динамика поступательного движения.
Динамика
вращательного движения.
Работа, энергия.
Законы сохранения.
Работа, энергия.
Законы сохранения.
Слайд 3Тема 1. Кинематика поступательного движения
План лекции
1.1. Основные понятия кинематики
1.2. Перемещение, скорость,
ускорение.
1.3. Обратная задача кинематики.
1.4. Тангенциальное и нормальное ускорения.
1.3. Обратная задача кинематики.
1.4. Тангенциальное и нормальное ускорения.
Слайд 41.1. Основные понятия кинематики
Механическое движение – это процесс перемещения тел или
их частей относительно друг друга.
Механическое, как и всякое другое, движение происходит в пространстве и времени.
Пространство и время – сложнейшие физические и философские категории.
В ходе развития физики и философии эти понятия претерпели существенные изменения.
Механическое, как и всякое другое, движение происходит в пространстве и времени.
Пространство и время – сложнейшие физические и философские категории.
В ходе развития физики и философии эти понятия претерпели существенные изменения.
Слайд 5 Классическую механику создал И. Ньютон.
Он постулировал, что время и пространство
абсолютны.
Абсолютное пространство и абсолютное время не взаимосвязаны.
Классическая механика приписывает абсолютному пространству и абсолютному времени вполне определенные свойства.
Абсолютное пространство и абсолютное время не взаимосвязаны.
Классическая механика приписывает абсолютному пространству и абсолютному времени вполне определенные свойства.
Слайд 6Абсолютное пространство
- трехмерно (имеет три измерения),
- непрерывно (его точки могут
быть сколь угодно близки друг к другу),
- эвклидово (его геометрия описывается геометрией Эвклида),
- однородно (в нем нет привилегированных точек),
- изотропно (в нем нет привилегированных направлений).
- эвклидово (его геометрия описывается геометрией Эвклида),
- однородно (в нем нет привилегированных точек),
- изотропно (в нем нет привилегированных направлений).
Слайд 7Абсолютное время
одномерно (имеет одно измерение);
непрерывно (два его мгновения могут
быть сколь угодно близки друг к другу);
однородно (в нем нет привилегированных мгновений);
- анизотропно (течет только в одном направлении).
однородно (в нем нет привилегированных мгновений);
- анизотропно (течет только в одном направлении).
Слайд 8В начале ХХ века классическая механика подверглась кардинальному пересмотру.
В результате
были созданы величайшие теории нашего времени – теория относительности и квантовая механика.
Теория относительности (релятивистская механика) описывает движение макроскопических тел, когда их скорость соизмерима со скоростью света.
Квантовая механика описывает движение микрообъектов.
Теория относительности (релятивистская механика) описывает движение макроскопических тел, когда их скорость соизмерима со скоростью света.
Квантовая механика описывает движение микрообъектов.
Слайд 9Теория относительности установила следующие положения о пространстве и времени.
Пространство и время:
-
не являются самостоятельными объектами;
– это формы существования материи;
- имеют не абсолютный, а относительный характер;
- неотделимы друг от друга;
- неотделимы от материи и её движения.
– это формы существования материи;
- имеют не абсолютный, а относительный характер;
- неотделимы друг от друга;
- неотделимы от материи и её движения.
Слайд 11Классическая механика изучает макроскопические тела, движущиеся с малыми скоростями.
Специальная теория относительности
изучает
макроскопические тела, движущиеся с большими скоростями (порядка С = 3 10 8 м/с) в инерциальных системах отсчёта.
Общая теория относительности изучает
макроскопические тела, движущиеся с большими скоростями в неинерциальных системах отсчёта.
Квантовая механика изучает микроскопические тела (микрочастицы), движущиеся с большими, но нерелятивистскими скоростями.
макроскопические тела, движущиеся с большими скоростями (порядка С = 3 10 8 м/с) в инерциальных системах отсчёта.
Общая теория относительности изучает
макроскопические тела, движущиеся с большими скоростями в неинерциальных системах отсчёта.
Квантовая механика изучает микроскопические тела (микрочастицы), движущиеся с большими, но нерелятивистскими скоростями.
Слайд 12Механика состоит из трех разделов – кинематики, динамики и статики.
Кинематика изучает
виды движений.
Динамика изучает причины, вызывающие тот или иной вид движения.
Статика изучает условия равновесия тел.
Динамика изучает причины, вызывающие тот или иной вид движения.
Статика изучает условия равновесия тел.
Слайд 13Основные понятия механики
Движение – изменение положения тел друг относительно друга.
Тело отсчёта
- тело, по отношению к которому определяется положение других тел.
Система отсчёта - система декартовых координат, связанная с телом отсчета и прибором для отсчета времени.
Материальная точка – это тело, формой и размерами которого в данной задаче можно пренебречь.
Абсолютно твердое тело – это тело, деформациями которого в данной задаче можно пренебречь.
Система отсчёта - система декартовых координат, связанная с телом отсчета и прибором для отсчета времени.
Материальная точка – это тело, формой и размерами которого в данной задаче можно пренебречь.
Абсолютно твердое тело – это тело, деформациями которого в данной задаче можно пренебречь.
Слайд 141.2. Перемещение, скорость, ускорение
Описать движение материальной точки – значит знать её
положение относительно выбранной системы отсчёта в любой момент времени.
Для решения этой задачи надо иметь эталон длины (например, линейку) и прибор для измерения времени – часы.
Выберем тело отсчёта и свяжем с ним прямоугольную систему координат.
Для решения этой задачи надо иметь эталон длины (например, линейку) и прибор для измерения времени – часы.
Выберем тело отсчёта и свяжем с ним прямоугольную систему координат.
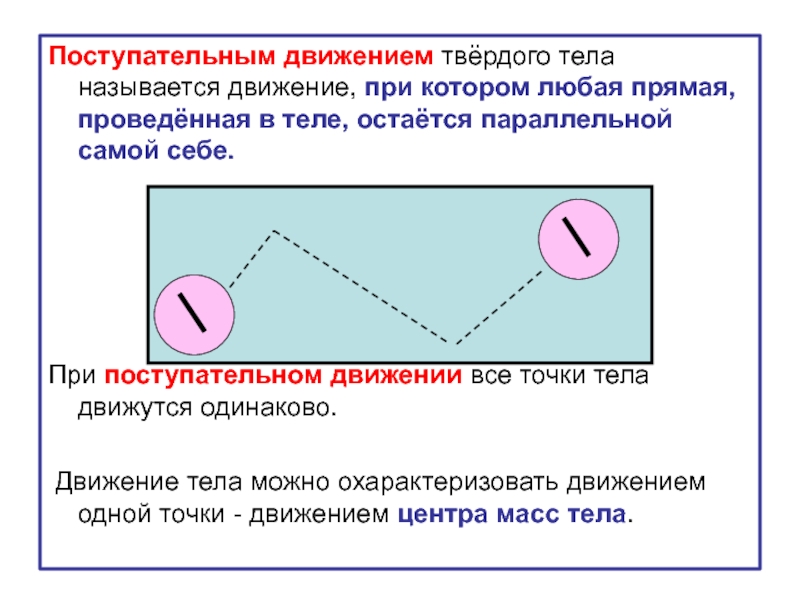
Слайд 15Поступательным движением твёрдого тела называется движение, при котором любая прямая, проведённая
в теле, остаётся параллельной самой себе.
При поступательном движении все точки тела движутся одинаково.
Движение тела можно охарактеризовать движением одной точки - движением центра масс тела.
При поступательном движении все точки тела движутся одинаково.
Движение тела можно охарактеризовать движением одной точки - движением центра масс тела.
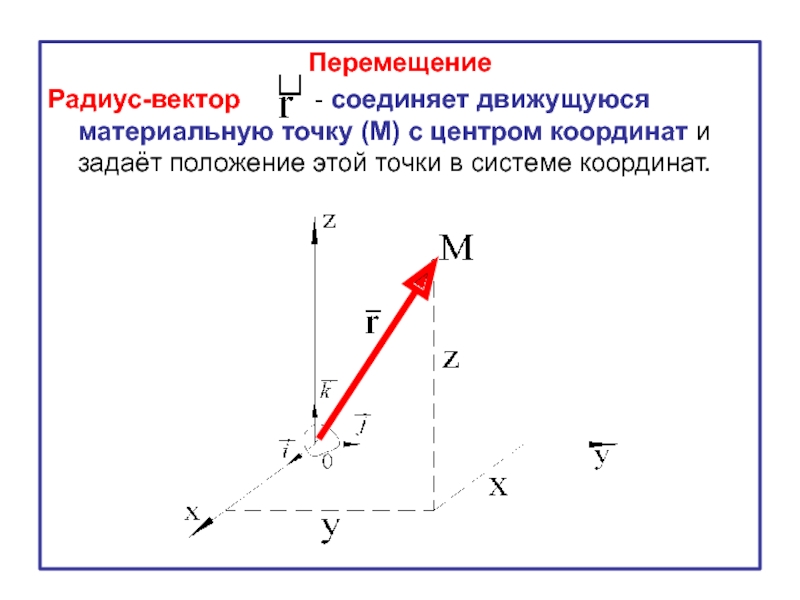
Слайд 16Перемещение
Радиус-вектор - соединяет движущуюся материальную точку (М)
с центром координат и задаёт положение этой точки в системе координат.
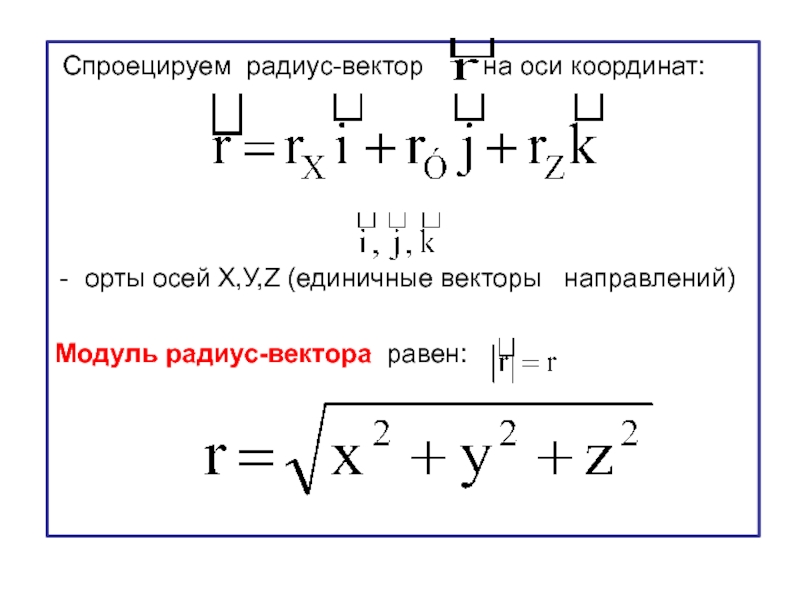
Слайд 17 Спроецируем радиус-вектор на оси координат:
орты осей Х,У,Z (единичные векторы направлений)
Модуль радиус-вектора равен:
Слайд 18
– проекции радиус-вектора
на соответствующие оси.
X, У, Z называются декартовыми координатами материальной точки.
на соответствующие оси.
X, У, Z называются декартовыми координатами материальной точки.
Слайд 19Траекторией называется линия:
которую описывает конец радиус-вектора материальной точки при её движении;
по
которой движется тело.
По виду траектории движения делятся на:
прямолинейное;
криволинейное;
по окружности.
По виду траектории движения делятся на:
прямолинейное;
криволинейное;
по окружности.
Слайд 20Законом движения материальной точки называется уравнение, выражающее зависимость её радиус-вектора от
времени:
Скалярная форма закона движения получила название кинематических уравнений движения:
Исключив из этой системы уравнений параметр времени t , получим уравнение траектории: У = f(X)
Скалярная форма закона движения получила название кинематических уравнений движения:
Исключив из этой системы уравнений параметр времени t , получим уравнение траектории: У = f(X)
Слайд 21Для конечных промежутков времени ∆t: Δt = t2 – t1
Вектор перемещения
соединяет начальную и конечную точки перемещения, пройденного телом за время Δt = t2 – t1.
Слайд 22
- приращение (изменение)
радиус – вектора.
Модуль вектора перемещения называется перемещением.
Путь - расстояние (S12), пройденное по траектории.
Перемещение и путь – величины скалярные и положительные.
Для конечных промежутков времени ∆t перемещение не равно пройденному пути:
радиус – вектора.
Модуль вектора перемещения называется перемещением.
Путь - расстояние (S12), пройденное по траектории.
Перемещение и путь – величины скалярные и положительные.
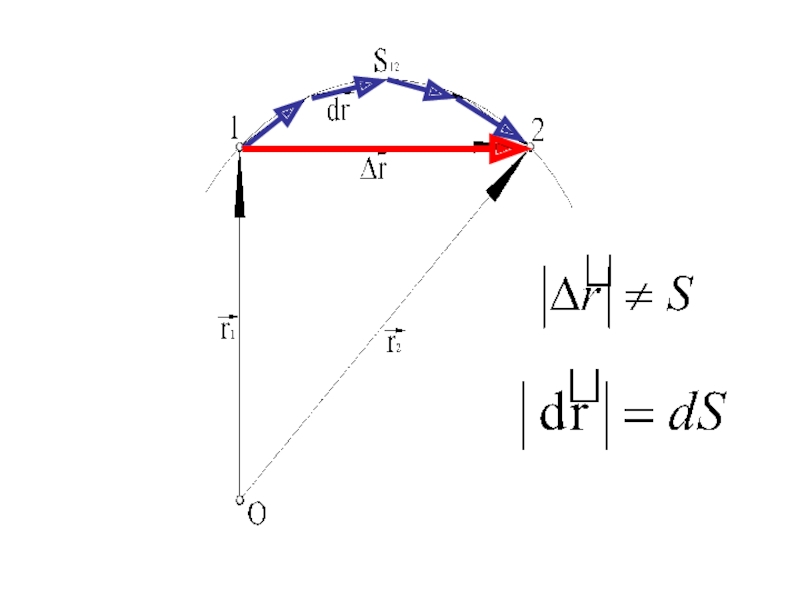
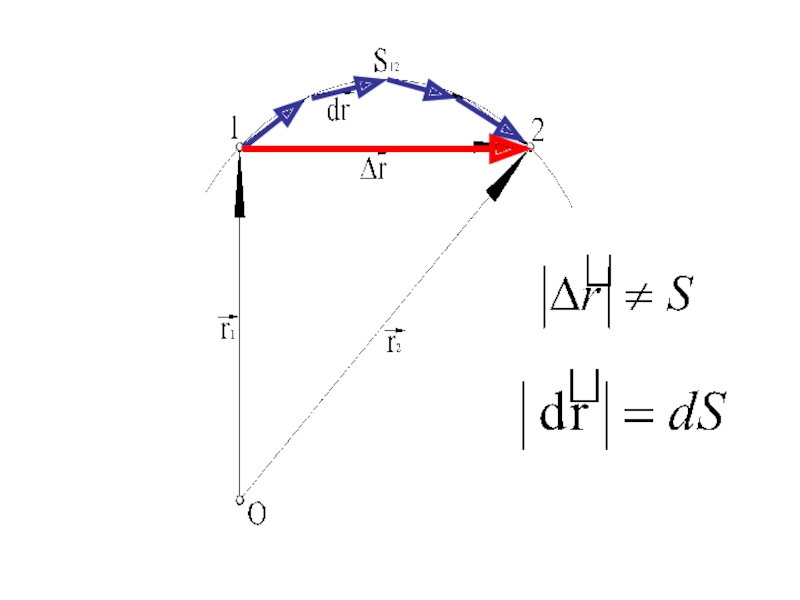
Для конечных промежутков времени ∆t перемещение не равно пройденному пути:
Слайд 23Для бесконечно малого промежутка времени dt:
- вектор элементарного перемещения;
- элементарное перемещение;
dS - элементарный путь.
Для бесконечно малых промежутков времени элементарное перемещение равно элементарному пути:
- элементарное перемещение;
dS - элементарный путь.
Для бесконечно малых промежутков времени элементарное перемещение равно элементарному пути:
Слайд 25Вектор перемещения получим, просуммировав векторы элементарных перемещений:
Перемещение получим, просуммировав элементарные перемещения:
Путь получим интегрированием (суммированием) элементарных путей или равнозначно модулей элементарных перемещений:
Слайд 27Скорость
- равна перемещению, совершенному материальной точкой за единицу времени;
характеризует быстроту изменения
пространственного положения материальной точки;
- измеряется в м/с;
- является векторной величиной;
- различают среднюю и мгновенную.
- измеряется в м/с;
- является векторной величиной;
- различают среднюю и мгновенную.
Слайд 28Вектор средней скорости за промежуток времени Δt:
- определяется как
- направлен вдоль вектора перемещения .
Слайд 31Мгновенная скорость равна пределу, к которому стремится вектор средней скорости при
неограниченном убывании промежутка времени до нуля (Δt→0).
Мгновенная скорость равна первой производной от радиус-вектора по времени.
Мгновенная скорость равна первой производной от радиус-вектора по времени.
Слайд 32Вектор мгновенной скорости направлен по
вектору
, т. е. по касательной к траектории.
Модуль мгновенной скорости равен первой производной от пути по времени:
Модуль мгновенной скорости равен первой производной от пути по времени:
Слайд 33Проекции скорости на координатные оси равны первым производным от соответствующих координат
по времени:
Слайд 34Вектор мгновенной скорости и его модуль V
через проекции скорости vx, vy, vz записываются как:
Слайд 35В процессе движения материальной точки модуль и направление её скорости в
общем случае изменяются.
1
2
Слайд 36Ускорение
- равно изменению скорости за единицу времени;
- характеризует быстроту изменения скорости
с течением времени;
- измеряется в м/с2;
- является векторной величиной;
- различают среднее и мгновенное.
- измеряется в м/с2;
- является векторной величиной;
- различают среднее и мгновенное.
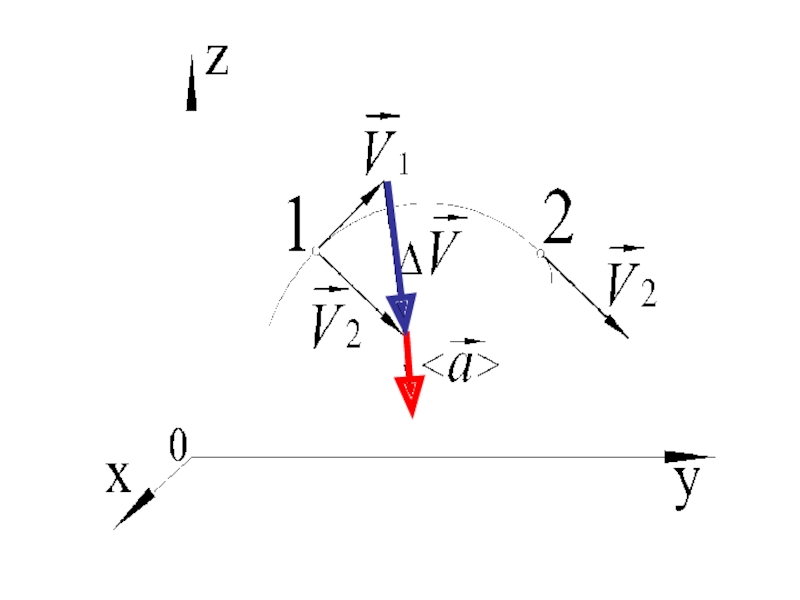
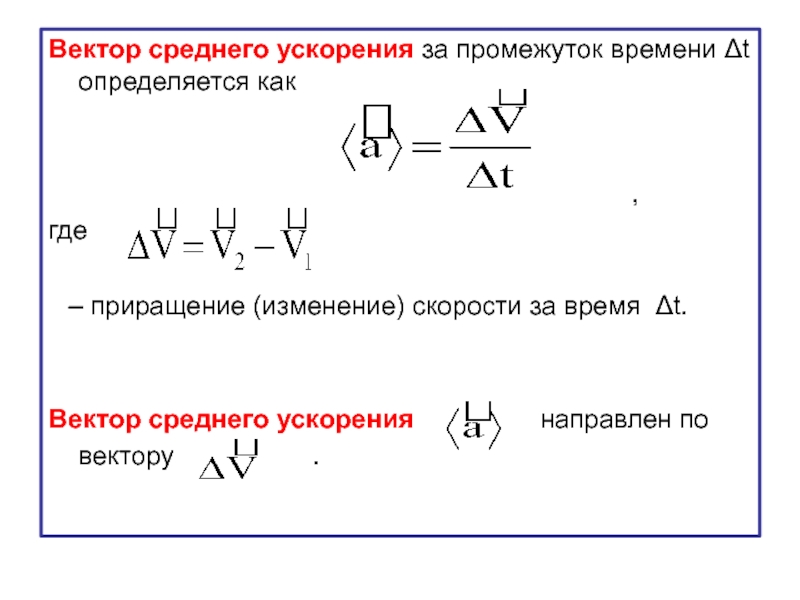
Слайд 38Вектор среднего ускорения за промежуток времени Δt определяется как
,
где
– приращение (изменение) скорости за время Δt.
Вектор среднего ускорения направлен по вектору .
где
– приращение (изменение) скорости за время Δt.
Вектор среднего ускорения направлен по вектору .
Слайд 39Мгновенное ускорение равно пределу, к которому стремится среднее ускорение при неограниченном
убывании промежутка времени до нуля ( Δt→0).
Мгновенное ускорение равно:
- первой производной от мгновенной скорости по времени;
- второй производной от радиус-вектора по времени.
Мгновенное ускорение равно:
- первой производной от мгновенной скорости по времени;
- второй производной от радиус-вектора по времени.
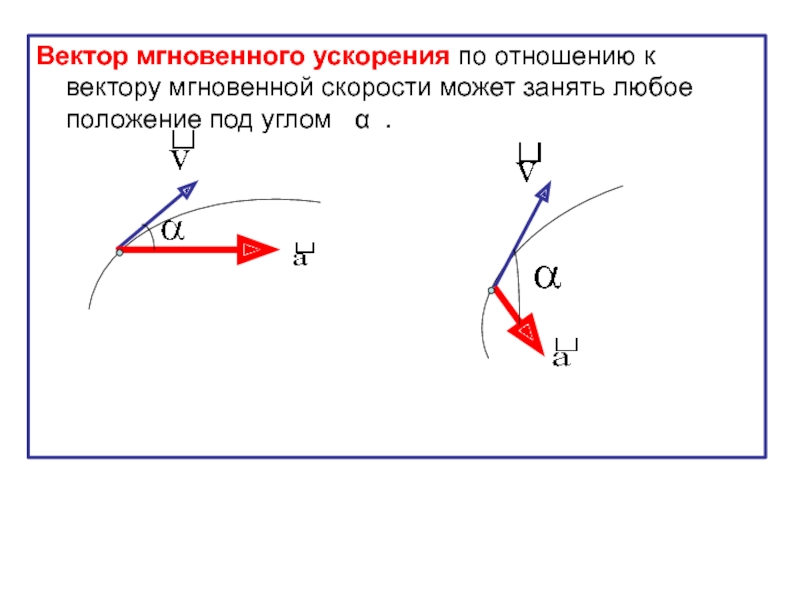
Слайд 40Вектор мгновенного ускорения по отношению к вектору мгновенной скорости может занять
любое положение под углом α .
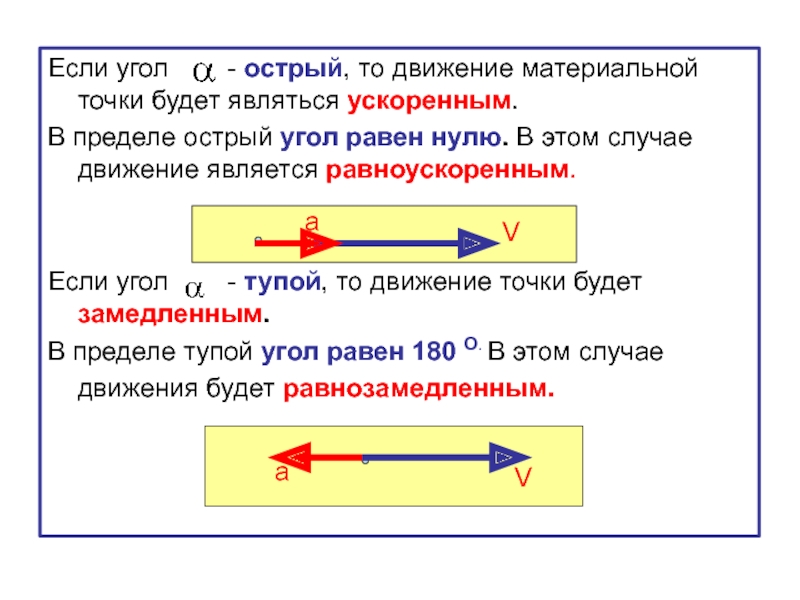
Слайд 41Если угол - острый, то движение материальной точки
будет являться ускоренным.
В пределе острый угол равен нулю. В этом случае движение является равноускоренным.
Если угол - тупой, то движение точки будет замедленным.
В пределе тупой угол равен 180 О. В этом случае движения будет равнозамедленным.
В пределе острый угол равен нулю. В этом случае движение является равноускоренным.
Если угол - тупой, то движение точки будет замедленным.
В пределе тупой угол равен 180 О. В этом случае движения будет равнозамедленным.
а
V
a
V
Слайд 42Проекции вектора ускорения на координатные оси равны первым производным от соответствующих
проекций скорости на эти же оси:
Слайд 441.3. Обратная задача кинематики
В рамках кинематики решаются две основные задачи: прямая
и обратная.
При решении прямой задачи по известному закону движения
в любой момент времени находятся все остальные кинематические характеристики материальной точки:
путь, перемещение, скорость, ускорение.
При решении прямой задачи по известному закону движения
в любой момент времени находятся все остальные кинематические характеристики материальной точки:
путь, перемещение, скорость, ускорение.
Слайд 45При решении обратной задачи по известной зависимости ускорения от времени
в любой момент времени находят скорость и положение материальной точки на траектории.
Для решения обратной задачи нужно задать в некоторый начальный момент времени tО
начальные условия:
радиус-вектор ;
скорость точки .
Слайд 47Окончательно скорость получим при решении данного выражения.
(1)
Из определения скорости следует, что элементарное перемещение равно
Из определения скорости следует, что элементарное перемещение равно
Слайд 48
Подставим сюда выражение для скорости и проинтегрируем полученное уравнение:
Окончательно для радиус-вектора имеем выражение:
Окончательно для радиус-вектора имеем выражение:
Слайд 49Частные случаи
Равномерное прямолинейное движение
(ускорение = 0 и
t0 = 0).
Тогда
Перейдём от векторной формы записи уравнений к скалярной:
Тогда
Перейдём от векторной формы записи уравнений к скалярной:
Слайд 521.4. Тангенциальное и нормальное ускорения
Пусть материальная точка движется по криволинейной траектории,
имея различную скорость в разных точках траектории.
Скорость при криволинейном движении может изменяться и по модулю и по направлению.
Эти изменения можно оценивать раздельно.
Скорость при криволинейном движении может изменяться и по модулю и по направлению.
Эти изменения можно оценивать раздельно.
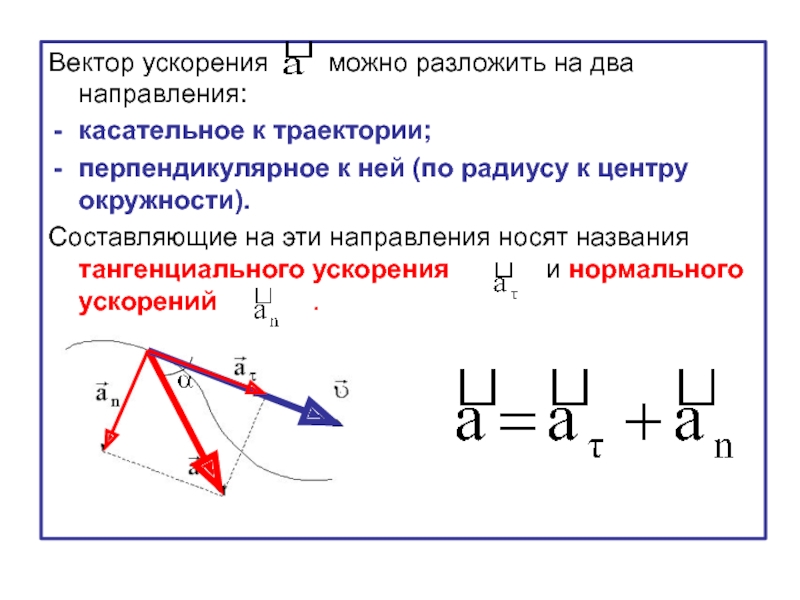
Слайд 53Вектор ускорения можно разложить на два направления:
касательное
к траектории;
перпендикулярное к ней (по радиусу к центру окружности).
Составляющие на эти направления носят названия тангенциального ускорения и нормального ускорений .
перпендикулярное к ней (по радиусу к центру окружности).
Составляющие на эти направления носят названия тангенциального ускорения и нормального ускорений .
Слайд 54Тангенциальное ускорение:
характеризует изменение скорости по модулю;
- направлено по касательной к траектории.
Модуль тангенциального ускорения равен модулю первой производной от скорости по времени.
Слайд 55Нормальное ускорение
характеризует изменение скорости по направлению;
направлено перпендикулярно скорости по радиусу
к центру кривизны траектории.
Модуль нормального ускорения равен
R – радиус кривизны в заданной точке траектории.
Модуль нормального ускорения равен
R – радиус кривизны в заданной точке траектории.
Слайд 57Частные случаи движений
= 0,
= 0
- равномерное прямолинейное движение;
= const, = 0
- равнопеременное прямолинейное движение;
= 0, = сonst
- равномерное движение по окружности;
4. = 0, = f(t)
- равномерное криволинейное движение.
- равномерное прямолинейное движение;
= const, = 0
- равнопеременное прямолинейное движение;
= 0, = сonst
- равномерное движение по окружности;
4. = 0, = f(t)
- равномерное криволинейное движение.
